导弹导引头伸出过程动力系统建模研究
徐子豪,王汉平,窦建中
(北京理工大学 宇航学院,北京 100081)
【装备理论与装备技术】
导弹导引头伸出过程动力系统建模研究
徐子豪,王汉平,窦建中
(北京理工大学 宇航学院,北京 100081)
基于气压传动原理,构建了导引头伸出动力系统的数学模型,借助于MSC.ADAMS的二次开发建立了动力系统与伸出机构相互作用的耦合仿真动力学模型,仿真获取了动力系统关键环节的伸出时间以及冲击载荷特性,导引头伸出时间的仿真值与实验结果吻合较好,且最大冲击载荷的仿真结果和理论预估值一致,这表明所建模型合理。仿真结果可为导引头机构与缓冲器的设计提供理论指导。
导弹导引头;气压传动;动力系统;多体动力学;耦合仿真
导弹导引头在导弹贮存和运输阶段,必须收缩在弹体之内并由舱盖封装,具有良好的保存环境,而在发射瞄准阶段,得借助一套导引头伸出机构渐次完成舱盖的开启和导引头伸出过程,以确保导引头快速、安全、可靠地伸出弹体,实现对视场目标的扫描和跟踪[1-4]。某地空弹的导引头伸出机构采用了一套由压缩气体作动力源、电爆阀为启控装置的气压驱动系统。该系统借助压缩气体先解锁舱盖,驱动舱盖开启,依靠舱盖的到位锁制器实现舱盖开启的到位锁定,同时借助舱盖的冲击作用,打开导引头伸出气缸的供气气路,最终完成导引头锁定销的解锁和导引头伸出的驱动过程。导引头伸出到位后,由导引头伸出机构箱体上的缓冲装置完成导引头的缓冲止动,从而实现导引头的可靠伸出。导引头伸出机构系统工作过程中,需要协调解决如何确保导引头的快速伸出和减小导引头伸出到位的缓冲制动载荷。导引头伸出速度快,意味着导引头伸出到位的冲击动量大,缓冲制动载荷也会增大,这对导引头的安全性提出了挑战。而要减小缓冲制动的载荷,一方面可考虑减小导引头伸出速度,另一方面也可考虑减小缓冲制动刚度。这些因素都制约了导引头伸出的快速性指标,对缓冲制动刚度设计及其结构设计提出了严格要求。为借助理论分析协调二者的关系,构建了导引头伸出动力系统的数学模型,并借助MSC.ADAMS的二次开发建立了动力系统与伸出机构相互作用的耦合仿真动力学模型[5],获取动力系统伸出时间以及缓冲载荷特性。仿真数据与试验结果的对比表明,导引头伸出时间吻合较好,这验证了模型的可信性;该建模仿真方法为导弹导引头伸出机构伸出时间与缓冲器刚度的优化匹配设计提供了重要的理论指导。
1 理论基础
1.1 气压传动原理
导弹导引头伸出系统的气动原理如图1所示:电爆阀起爆,打开高压气瓶,气流将通过气路流入舱盖锁定销气缸中,随着气流压力增大,舱盖锁定销被打开,此时舱盖的锁定被解除;气流进而流入舱盖驱动气缸,从而驱动舱盖向开启的方向运动,舱盖得以打开,为导引头伸出让出通道;当舱盖撞上B点时,舱盖被到位锁定销锁定,同时,流向导引头锁定销气缸的气路被打开,气流流入导引头锁定销气缸,进而解锁导引头锁定销,在导引头锁定销解锁的同时,通往导引头伸出气缸的气路接通,气流流入导引头气缸,最终推动导引头伸出活塞顶着导引头伸出,导引头伸出到位后,由安装在安装箱体上的缓冲装置对导引头缓冲制动,最终实现导引头的伸出[6]。

图1 气压传动原理图
其中,m1、m2、m3、m4分别表示每段节流孔及管路中流过的质量,P1、T1,P2、T2,P3、T3,P4、T4,P5、T5分别表示高压气瓶、盖锁定销、盖驱动缸、导引头驱动缸、导引头锁定销和导引头气缸的压强和温度。
1.2 导引头驱动过程的耦合实现
在MSC.ADAMS中,分别将Pi、Ti、mi和vi定义为状态变量,并使用ADAMS内置的DIF、DIF1函数将描述动力系统的动力学模型表述成ADAMS中的微分方程,这样,借助vi将机构运动特性引入动力系统方程,而将Pi·Si作为作动活塞、锁定销的驱动载荷,从而实现动力系统与机构动态特性的耦合。
其中,i=(1,2,3,4,5),分别表示每段节流孔及管路。P、T、m、v分别表示压强、温度、节流孔流过气体的质量以及速度。
2 动力系统建模
2.1 动力系统模型
2.1.1 模型假设
由于导引头伸出过程时间较短,气体对外的热交换不充分,可以假设动力系统中气体的状态变化过程为绝热过程。同时,因为机构系统中的润滑条件较好,可以忽略机构运动摩擦的影响,管道理想化为薄壁管模型[7-8]。而气体在气缸之间的流动阻尼,主要由局部的湍流阻尼和气体的粘性阻尼两部分组成。
2.1.2 薄壁管的阻尼特性
薄壁管具有一定容积,它在高压气瓶工作期间容纳一定气体,容纳的气体质量与压强、温度等状态参数有关。把薄壁管假想为只有阻尼的毛细管节流孔,其阻尼为沿程阻尼和局部阻尼之和[9]。其中,沿程压降ΔPy和局部压降ΔPj分别为:
(1)
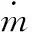
因此,全程压降为ΔP=ΔPy+ΔPj,ΔP=Pi-Pi+1,ρi=Pi/(RTi)。由以上各式可得出每段节流孔质量流量为:
(2)
2.1.3 气动过程动力学方程
1) 气瓶的状态方程
P1V1=M1RT1
(3)
(4)
(5)
式中:M1=m10-m1,m10=P0V10/(RT0),V10为气瓶的初始体积,P0、T0为高压气瓶初始压强与温度。
2) 舱盖锁定销缸状态方程
P2V2=M2RT2
(6)
(7)
根据能量守恒可得微分:
d(cpT1m1)-d(cpT2m2)=d(cvT2M2)+d(P2V2)
(8)
(9)
式中:l2为舱盖锁定销的位移, 0.005 9为舱盖锁定销缸与第二段管路接通的临界值,cp为定压比热容,cv为定容比热容,M2=m1-m2+m20,m20=PhV20/(RT0),Ph为大气压,V20为舱盖锁定销缸的初始体积,S2为舱盖锁定销缸的横截面积,v2为舱盖锁定销的速度。
3) 舱盖驱动缸的状态方程
P3V3=M3RT3
(10)
(11)
根据能量守恒可得微分:
d(cpT2m2)-d(cpT3m3)=d(cvT3M3)+d(P3V3)
(12)
(13)
式中:M3=m2-m3+m30,m30=PhV30/(RT0),V30为舱盖驱动缸的初始体积,S3为舱盖驱动缸的横截面积,v3为舱盖活塞杆的速度。
4) 导引头锁定销缸的状态方程
P4V4=M4RT4
(14)
(15)
根据能量守恒可得微分:
d(cpT4m3)-d(cpT4m4)=d(cvT4M4)+d(P4V4)
(16)
(17)
式中:l4为导引头锁定销的位移,0.0059为导引头锁定销缸与第四段管路接通的临界值,M4=m3-m4+m40,m40=PhV40/(RT0),V40为导引头锁定销缸的初始体积,S4为导引头锁定销缸的横截面积,v4为导引头锁定销的速度。
5) 导引头气缸的状态方程
P5V5=M5RT5
(18)
(19)
根据能量守恒可得微分:
d(cpT1m1)-d(cpT2m2)=d(cvT2M2)+d(P2V2)
(20)
(21)
式中:M5=m50+m4,m50=P0V50/(RT0),V50为导引头气缸的初始体积,S5为导引头气缸的横截面积,v5为导引头活塞杆速度。
2.2 机构动力学模型
导引头伸出机构可分解为14个具有相对运动的刚体。
箱体上有导槽、舱盖活塞杆上有滑槽,舱盖与箱体、舱盖活塞杆之间均由四个销轴予以约束,四个销轴可在导槽和滑槽中运动,从而实现舱盖的内缩和开盖过程。舱盖靠两个以移动副约束在箱体上的锁定销锁定,锁定由接触建模实现,舱盖锁定销与箱体之间定义了弹簧锁定力,弹簧考虑了预压特性,当气动力F2=P2·S2足够大,使舱盖锁定销压缩弹簧有足够的行程之后,舱盖锁定销与舱盖之间不再接触,从而实现舱盖解锁。舱盖驱动缸与舱盖活塞杆之间为移动副约束,并在舱盖驱动缸与盖活塞杆之间添加了单组分力,其力大小等于舱盖驱动缸内的压强与活塞的有效作用面积的乘积,即F3=P3·S3。舱盖活塞杆与箱体之间设定了接触传感器,当舱盖活塞杆运动形成达到极限后即触发传感器,接通舱盖驱动气缸与导引头锁定销气缸的气路;导引头锁定销与箱体之间也定义了移动副约束,并在导引头锁定销与箱体间定义了预压弹簧力,当导引头锁定销缸中的气动力F4=P4·S4足够大时,将驱动导引头锁定销运动,使导引头锁定销与导引头脱离接触,实现解锁;导引头气缸与盖驱动缸之间采用了固定约束,而导引头气缸与导引头活塞之间则为移动副,并在导引头气缸和导引头活塞之间添加了单组分力,其力大小等于导引头气缸内的压力与活塞的有效作用面积的乘积,也就是F5=P5·S5。
接触建模均基于赫兹接触理论[11]。它建立了刚体与刚体之间的接触力。该模型刚体之间总共有28个接触力。

图2 导引头伸出机构系统模型
导引头的缓冲制动采用单边冲击函数IMPACT来实现,IMPACT函数模型为:
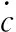
1) 函数中刚度系数k的确定
根据文献[12]的推导,刚度系数k的计算公式为:
(22)

2) 函数中阻尼系数cmax的确定
根据文献[13-14]的推导,阻尼系数cmax的计算公式为:
(23)

3 结果分析
3.1 针对实验状态的仿真结果及数据对比
图3表明高压气瓶气体膨胀做功,其压强P1逐渐减小,而T1与P1正相关,该结果与数学模型的定性分析相吻合。

图3 P1和T1的时间历程
图4中压强P3和温度T3在初始段均为恒定值,这是由于在舱盖打开之前,舱盖锁定销锁死了后续的气路,气流无法流入舱盖驱动缸;当舱盖锁定销打开之后,气路接通,舱盖驱动缸的压强P3增大,气瓶对舱盖驱动缸内气体作功,T3升高,当P3达到能推动舱盖运动时,气体对舱盖作功,内能转化为机械能,P3、T3下降。第二个突变点是由舱盖撞上开关B并止动所致,气流继续流入舱盖驱动缸中,P3增大,对原有气体作功完成之后,气体会流出舱盖驱动缸,T3基本保持不变。

图4 P3和T3的时间历程
图5中压强P5和温度T5在初始段均为恒定值,这是由于在舱盖打开并撞上开关B之前,导引头锁定销锁死了后续的气路,气流无法流入导引头气缸;当舱盖撞击开关B之后,气路接通,导引头气缸的压强P5增大,气瓶对导引头驱动缸内气体作功,T5升高,当P5达到能推动导引头运动时,气体对导引头作功,内能转化为机械能,P5下降。第二个突变点则是由导引头止动所致,此时导引头驱动缸体积不变,且不断有气体流入其中,所以P5、T5升高。

图5 P5、T5的时间历程
图6中曲线的初始段是0,这是舱盖锁定销解锁阶段,气流尚未流入舱盖驱动缸;舱盖锁定销解锁后,气流流入舱盖驱动缸,从而驱动舱盖运动,盖驱动缸压强增大,对舱盖的驱动力增大,所以舱盖的速度和位移也不断增大,直到舱盖撞击B点为止;后续的稳定段是到位锁定销将舱盖锁死之后的状态。可以看出,舱盖的最大开启速度达6.36 m/s。

图6 舱盖开启速度和位移时程
图7中曲线的初始段为0,这是由于前段的气路尚未接通。待舱盖撞击B点接通导引头驱动缸,实现对导引头驱动缸的通气之后,气流不断流入导引头驱动缸,导引头驱动缸压强增大,对导引头的驱动力增大,所以导引头的速度和位移也不断增大,直到伸出到位,缓冲止动为止。导引头的伸出最大速度为0.436 m/s。

图7 导引头伸出速度和位移时程
从图8可以看出,从导引头伸出机构开始工作到伸出到位的时间为0.531 s。导引头制动过程中对驱动缸的冲击载荷大小为278 N。

图8 导引头伸出到位的冲击载荷
对比假设的绝热模型以及实验所得的时间数据可得表1。

表1 导引头伸出时间的仿真值与实验数据的对比
由表1可知,绝热状态下仿真结果与实验数据误差为3.45 %,具有较高的精度,这表明模型所作的假设是合理的,仿真模型可信。
3.2 冲击载荷的分析
冲击载荷大小
F=Fk+Fd
(24)
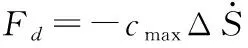
4 结论
基于绝热过程假设的动力学模型仿真结果表明:
1) 导引头伸出过程正常,伸出时间为0.531s,与实验测试时间0.55s吻合较好,说明绝热模型合理,仿真结果可信。
2) 导引头缓冲的仿真冲击载荷为278N,与理论预测的331N吻合较好,说明仿真模型中的碰撞模型设置合理;冲击载荷较小,也验证了实验中导引头的可靠缓冲。
3) 仿真所得伸出时间比实测时间要短,可能原因如下:
a) 气路阻尼的影响。因为整个动力系统的气路直径小,且有很多拐角之处,增大了气路阻尼,导致气路压降的增大。
b) 电爆管的爆炸与动力系统开始工作之间存在时间滞后,目前仿真模型无法表述。
c) 模型当中摩擦的影响,尤其是开盖气缸与活塞之间、导引头伸出气缸与活塞之间的摩擦的影响,摩擦的这种影响比较复杂,在目前仿真模型中较难以真实表述。
[1] 徐春夷.国外导引头技术现状及发展趋势[J].制导与引信,2012,33(2).
[2] 柴世杰, 李建勋, 童中翔,等.空空导弹红外导引头建模与抗干扰仿真[J].兵工学报,2014,35(5):681-690.
[3] 李成, 李建勋, 童中翔, 等.红外成像制导末端局部图像识别跟踪研究[J].兵工学报,2015,36(7):1213-1221.
[4] 汤永涛,林鸿生,陈春.现代导弹导引头发展综述[J].制导与引信,2014,01:12-17.[5] 胡胜海, 郭春阳, 余伟, 等.基于变胞原理的舰炮装填机构刚-柔耦合动力学建模及误差分析[J].兵工学报,2015,36(8):1398-1404.
[6] 李笑,吴冉泉,官忠范.液压与气压传动[M].北京:国防工业出版社,2006.3,190-201.
[7] 张也影.流体力学[M].2版.北京:高等教育出版社,2011.
[8] 王保国,刘淑艳,黄伟光.气体动力学[M].2版.北京:北京理工大学出版社,2006.
[9] 王汉平,张聘义,邵自然.混合连通式油气悬挂重型车辆的振动性能研究[J].导弹与航天运载技术,2003,04:7-11.
[10]成大先.机械设计手册:单行本.气压传动[M].5版.北京:化学工业出版社,2010(1):29-30.
[11]章伊华, 林丹益, YANG Guo-yu.基于接触理论的螺栓联接接触面力学特性研究[J].兵工学报,2015,36(5):946-952.
[12]段玥晨.考虑刚柔耦合效应的柔性多体系统碰撞动力学研究[D].南京:南京理工大学,2012:26.
[13]安雪斌,潘尚峰.多体系统动力学仿真中的接触碰撞模型分析[J].计算机仿真,2008,10:98-101.
[14]HAMID M.LANKARANI,PARVIZ E.NIKRAVESH.Continuous Contact Force Models for Impact Analysis in Multibody Systems[J].Nonlinear Dynamics,1994(5):193 -207.
[15]王欢,白杨,江晟.某型导引头半物理仿真系统设计[J].四川兵工学报,2015(5):24-27.
[16]何昌见,孟秀云,何湘.谐波雷达导引头目标信息估计算法[J].探测与控制学报,2015(4):24-29.
(责任编辑 周江川)
Study Concerning the Dynamical System Model of Missile Seeker Protruding Process
XU Zi-hao, WANG Han-ping, DOU Jian-zhong
(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)
Based on the principle of pneumatic drive, a mathematical model of dynamical system which makes the seeker out of seeker cabin was built. By means of the secondary development of MSC.ADAMS, a coupling dynamics simulation model was established, in which the dynamical system and the protruding structure of seeker were interactive. The protruding time of seeker and the impact load of seeker were obtained. The simulation result is in good agreements with the testing data and the theoretical values, which indicates that the model is reasonable. The simulation result could provide a theoretical guidance for design of the seeker and the bumper.
missile seeker; pneumatic drive; dynamical system; multi-body dynamics; coupling simulation
2016-04-12;
2016-05-10
徐子豪(1991—),男,硕士研究生,主要从事兵器科学与技术研究。
10.11809/scbgxb2016.10.004
徐子豪,王汉平,窦建中.导弹导引头伸出过程动力系统建模研究[J].兵器装备工程学报,2016(10):19-23.
format:XU Zi-hao, WANG Han-ping, DOU Jian-zhong.Study Concerning the Dynamical System Model of Missile Seeker Protruding Process[J].Journal of Ordnance Equipment Engineering,2016(10):19-23.
TJ761.1
A
2096-2304(2016)10-0019-06

