超声速弹丸高空流场数值模拟与稀薄气体效应研究

王 勇，王学德，许国龙

(南京理工大学 能源与动力工程学院， 南京 210094)



【装备理论与装备技术】

超声速弹丸高空流场数值模拟与稀薄气体效应研究

王 勇，王学德，许国龙

(南京理工大学 能源与动力工程学院， 南京 210094)

利用直角坐标网格技术研究高超声速稀薄气体流动的DSMC模拟方法，编制了高空弹丸外流场数值模拟通用计算程序，将本方法的计算结果与有关文献中公布的理论模型数据进行了对比，验证本方法的正确性。模拟了稀薄流下不同海拔高度尖拱型弹头和其他外形弹头的在超声速来流中的流场，并推广至不同外形弹头气动受力情况的计算，研究其稀薄效应。分析比较发现了随着海拔高度的升高，稀薄效应使弹丸的激波层厚度增加，外部流场压缩性减弱，表面的热流密度有所降低。相比于尖拱型弹头，钝头弹丸在驻点处所受的压力较小，尾部较强，符合高超声速飞行器钝头弹体的受力规律。

超声速；数值模拟；稀薄流；稀薄效应

现代战争迫使弹箭的飞行高度越来越高。对于高空飞行的飞行器而言，气体稀薄效应越发显著。对于高空弹箭而言，由于空气稀薄，经典气体动力学的连续介质假设不成立，无法用传统的Navier-Stokes方程求解，必须采用一种新的方法。DSMC方法使用大量的模拟分子代表真实气体并模拟真实分子的运动和碰撞，通过计算机来直接模拟流场本身，摒除了数学求解的困难，并且将模拟分子的运动信息进行存储，目前已经相当成功地应用到了各个行业的诸多方面。如美国航天飞机升阻比的计算、长征-4B火箭推进剂在轨排放扰动力矩的计算、美国通讯衰减飞行试验中的电子密度分布计算等等。有效地分析气动力参数对于高空超音速弹箭至关重要，是其安全飞行的基础，准确模拟高速稀薄气流如今只能采用DSMC算法。

国外对于高空稀薄流的研究更早也更加深入,如G.A.Bird[1]关于DSMC算法在航天飞行器上的应用。国内的DSMC研究起步较晚但是发展速度非常快并且基本成型，李学东、黄海龙等人[2-4]采用非结构化三角网格，利用VHS分子模型、CLL反射模型对高超音速气体绕圆柱流动问题进行了数值模拟，蔡国飙[5]、叶友达[6]则分别论述了DSMC的时间步长和高空飞行器的气动特性，但对于高空超音速弹丸的稀薄流场研究较少。

本文采用直角坐标网格技术研究高超声速稀薄气体流动的DSMC模拟方法，选用由Thacker、Gonzalez和Putland在1980年提出的传统的四叉树方法生成直角坐标网格,分子碰撞模型采取VHS变径硬球模型。模拟计算了二维稀薄气流下60 km和80 km高空的超音速平板绕流，并与公布的文献数据进行对比验证，计算了不同海拔高度下尖拱型弹丸以及其他外形弹头在超声速稀薄来流的流场，发现随着海拔高度的升高，由于高空的稀薄效应使外部流场激波层厚度增加，弹体表面热流度沿轴线降低等现象。尖拱型弹丸头部由于连续外凸的表面，其形成的激波尾部明显宽于抛物线型弹丸，表现为对弹头尾部流域的影响更为强烈。

1 数值模拟方法

Bird发展的DSMC(Direct Simulation Monte-Carlo)方法[7]直接从流动的物理模拟出发，根据分子动力学方法，采取概率论判断分子间是否发生碰撞。DSMC方法用大量的模拟分子来模拟真实的气体，将模拟分子的空间坐标、速度、内能等数据进行储存，并随着分子的运动、碰撞和与边界的作用而变化，模拟所用的时间应该与实际情况的时间一致。整个过程是非定常的，经过足够长时间的模拟后，可以认为流动状态达到了定常流。DSMC对于求解过渡领域流场的总体效应方面和精细结构方面均可以得到与实验准确相符的结果，该方法对于复杂外形的航天飞机在过渡区所得结果与飞行测量数据的一致性很好[1]。

DSMC计算方法主要是模拟分子的微观运动和分子间的碰撞，而分子的运动和碰撞一般是耦合在一起的，常用的数值模拟方法很难将二者解耦，因此，对于使用DSMC模拟稀薄流场时分子的运动和碰撞需要特别处理。在一个时间步长Δt内，先让各个分子按照各自的速度运动一段距离，再按照碰撞模型以真实的碰撞频率选出碰撞对，分配碰撞后的分子速度和内能，并确定是否发生化学反应。Δt的取值应该小于平均碰撞时间，通过空间网格计算碰撞并对气体分子量进行统计得到宏观量，网格的尺寸与分子平均自由程相比应该足够小。碰撞只会在同一网格间发生，从而实现分子运动和碰撞的解耦。模拟计算初始时需给定计算域内模拟分子的位置和速度，而后在每一个时间步长内，处理分子运动和碰撞，分子的运动超出所设定的边界，考虑其与边界的相互作用，引入相应的反射模型，分子间的碰撞处理方式主要是分子碰撞的取样，即恰当的选择碰撞对并实现一定数目的碰撞，这是使Δt时间内碰撞与运动匹配，使模拟与真实流动过程一致的关键。

2 直角坐标网格生成

DSMC方法中的网格选取十分关键，关系着分子碰撞对的选取和流场的正确取样。对于同样的流场，如果用不同类型的网格进行模拟，结果也可能不同。所要求网格的尺度要小于当地平均自由程，并保证网格划分足够精细，使网格内的参数均匀的假设充分成立。在本研究中，考虑到物面形状、计算耗时以及计算精度等原因，选用传统的四叉树方法生成网格。

通常在流场的模拟中物面边界的形状千差万别，网格的属性也不相同，除去流场网格和固体网格还有物面网格，本研究采用限制盒技术，去掉了外部大部分流场网格，然后使用Painting algorithms[8]方法筛选剩余网格。首先在物面外部选择一个网格，然后在这个网格所有的相邻网格单元中进行搜索。如果被搜索到的这个网格与物面不相交，那么将这个网格进行标识，放入“存储库”中。如果这个网格和物面相交，那么不做标识。搜索完这个网格相邻的所有网格后，在“储存库”中取出一个网格再进行上述运算，直到库中没有网格为止。

对于物面边界而言，其与网格相交被切割成很多个离散的线段。当分子和物面发生碰撞时，可以认为一条完整的物面边界所受到的分子碰撞等于各个离散线段受到的分子碰撞之和。而本研究中所讨论的离散线段应起始于网格的一边，终止与该网格的另一条边。因此，首先将一整条物面边界分成若干离散线段，然后统计离散线段的起始位置和终止位置，并对每条线段编号。在与网格相交时，会出现线段长度较小的情况，如图1所示。这种长度较小的情况不能忽略。在程序的设计中，规定了可识别的最小长度k。凡是低于长度k的都属于长度较小的情况。这较短的线段应该添加进它之前的线段，然后再对新线段进行k值判断，直到所有的线段长度都符合要求。接下来模拟每条离散线段的分子碰撞情况，最后将这些数据进行汇总，得到这条完整的物面边界的模拟结果。

图1 线段的合并

3 高空稀薄流场数值模拟的验证

3.1 计算区域和网格

选取的计算网格模型为平板，如图2所示，计算区域为(0.0 m，1.0 m)×(0.0 m，0.6 m)，网格类型为结构网格。网格单元数为6 000，网格节点数为6 197。流场的下边界为对称边界，左侧和上边界为自由来流，流场右侧设为真空。

图2 计算网格

3.2 计算条件

来流为空气，其中氮气和氧气的组分分别为0.79和0.21，其他组分的气体因其所占比例较少而忽略不计。来流温度为300 K，来流速度为1 412.5 m/s。氮气分子的质量为4.65×10-26kg黏性系数的温度指数为0.74，氧气分子的质量为5.312×10-26kg，黏性系数的温度指数为0.77。随着高度的变化，分子数密度也不同，在60 km高度上，分子数密度5.995×1021m3。在80 km高度，分子数密度变为3.264 2×1020m3。采用不同的分子数密度模拟了不同高度环境下的平板绕流流场情况。

3.3 计算结果分析

图3是两种高度下平板绕流的密度分布云图。超音速来流横掠平板时，在前缘点形成了斜激波，并且在前缘点附近激波与边界层相互作用相互影响并且逐渐合并。在距前缘点十几个分子自由程的位置，二者开始发生分离。平板上方的流场受到了平板前缘扰动的影响，而超声速来流在流经平板后，在流场的右侧边界也就是真空处，密度迅速下降。对比60 km和80 km两种工况，随着高度的增加，流场密度也逐渐减小，可以看出气体稀薄程度对流场的影响。图4是不同高度下流场温度分布云图，因为在初始边界条件设定时，设壁面为等温边界，这就使得靠近壁面区域的温度最高，不但高于激波后的温度，也高于壁面温度。前缘产生的扰动影响到了上游温度分布，可以看出其温度逐渐升高。图5显示了不同高度下的流场压力分布，经过斜激波后压力增加，在前缘点附近压力增加到最大。沿平板表面方向气体流动速度不断加快，压力也随之减小，因为流场右侧设为真空边界，压力在这里迅速降低。高度的增加也会导致流场各处压力减小。这是因为在微观上，压力可以解释为单位时间内无数个气体分子热运动对物面的撞击作用力。在相同的来流速度下，空气越稀薄，与壁面发生碰撞的分子数越少，压力越小。

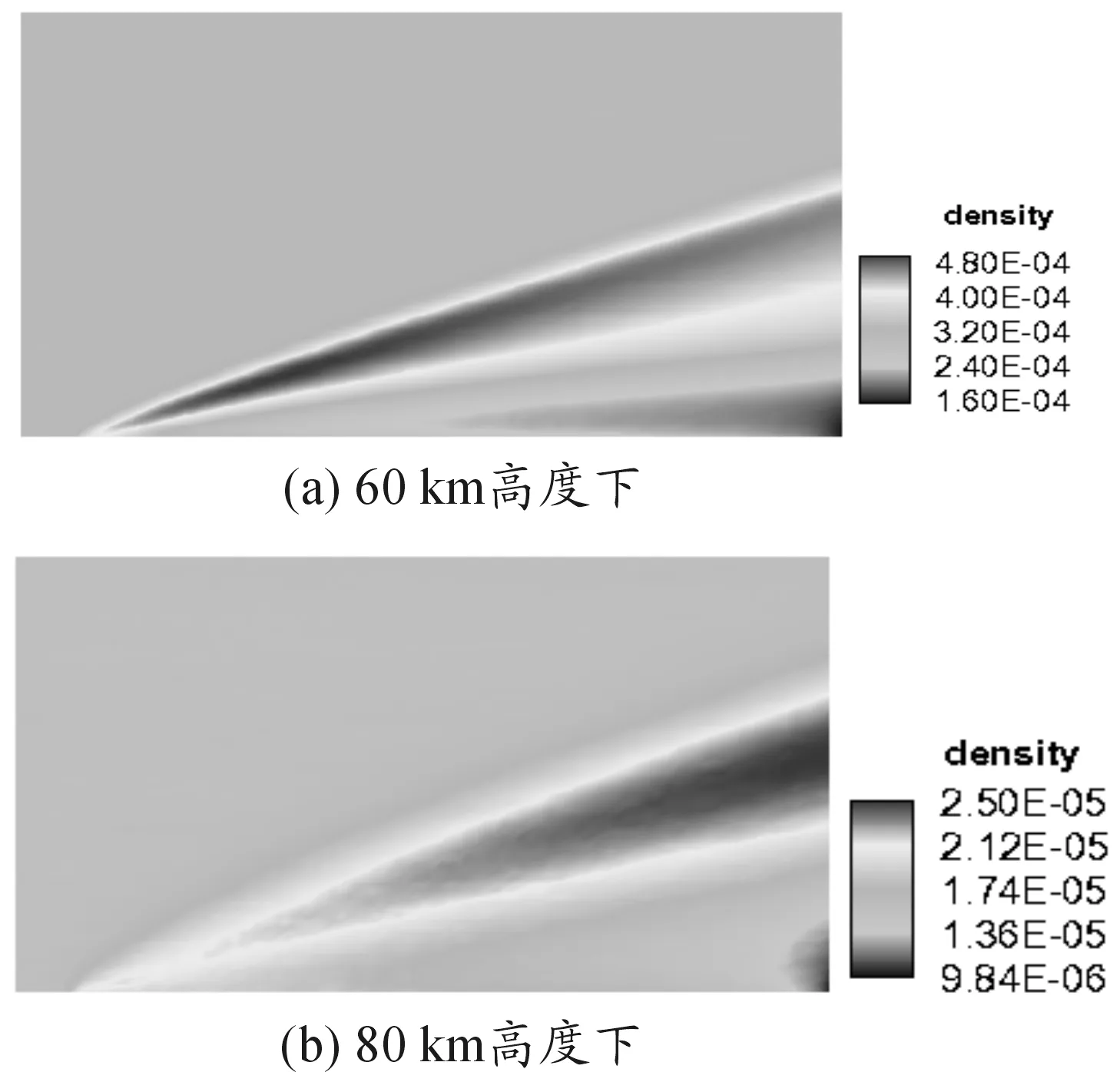
图3 不同高度平板绕流的密度分布云图

图4 不同高度平板绕流的温度分布云图

图5 不同高度平板绕流的压力分布云图

图6是60 km高度下平板表面系数的计算数值图，其中压力系数、摩擦因数和热流通量都和文献[7]进行了对比，可以看出在平板中部，热流量较实验值偏小，这是由于壁面设定的等温条件，而实际情况该部位温度由于分子摩擦温度会升高。尾部由于平板右侧的真空条件，使得模拟数据有小幅波动，但总体的变化趋势基本一致，说明了此方法可行。

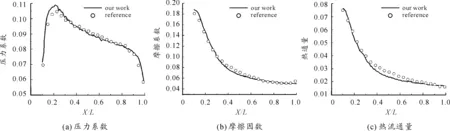
图6 平板表面各计算量与文献数据的比较

4 超声速弹丸高空流场数值模拟

4.1 尖拱型母线弹头

弹丸外形如图7所示，弹头部分为相切尖拱型。计算网格区域为(0.0 m,1.0 m)×(0.0 m,0.6 m)，计算区域的左边界和上边界为自由来流边界，右面边界为真空边界，下边界是对称边界。流场共2 430个网格，2 576个节点。计算条件来流为空气，氮气氧气分别占79%和21%，其他气体所占组分较小不予考虑。来流温度300 K，气流速度为1 412.5 m/s，高度不同，来流的分子数密度也不同。

图7 弹头外形

4.2 计算结果分析

图8给出了高空环境下的流场密度云图，可以看出，在高空超音速的工况下，在弹头的前部形成了十分显著的斜激波。在弹头前部驻点附近密度较大，气流经过激波后密度逐渐减小。在靠近右侧边界，距离弹体附面层较近的地方，密度迅速减小。并且对比60 km和80 km下的两种工况可以看出二者的激波形状略有差异。60 km工况下产生的激波更加贴体，同时受高空气体稀薄效应影响，80 km工况下流场的各点密度较60 km时小。图9给出了不同高度下流场温度分布云图，驻点处的温度依然最大，过驻点处，弹体表面承受着主要的气动热，这一部位的气动烧蚀也最为显著。沿弹体的轴线方向，温度逐渐降低。图10给出了不同高度下的流场速度分布云图，可以清楚看到，经过斜激波后，速度逐渐减小，在弹体表面处，气体有一定的滑移速度。沿弹体表面速度逐渐减小直至亚音速流动，但是不会减小到零。这是因为在高空稀薄气体环境下，气体分子之间的平均自由程要大得多，在气体分子同弹体表面发生碰撞以后，相当一部分的分子反射出去后没有发生二次碰撞，这就表现为图中所示的气流滑移现象。图11给出了不同高度表面分布量计算结果，压力系数在头部驻点处最大，沿弹丸轴线逐渐下降，最后趋于平缓，摩擦因数和热流通量变化也大致相同。

图8 不同高度下相切尖拱型弹头流场密度分布云图

图9 不同高度下相切尖拱型弹头流场温度分布云图

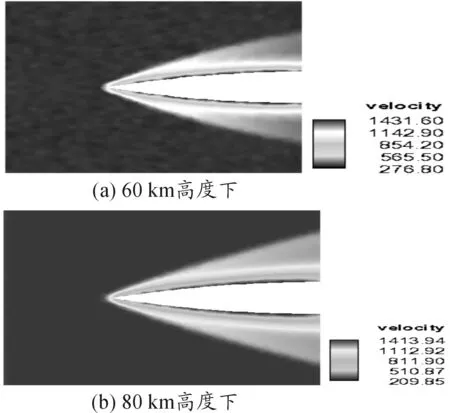
图10 不同高度下相切尖拱型弹头流场速度分布云图

图11 相切尖拱型弹头不同高度表面分布量计算结果

4.3 其他外形弹头

采用DSMC算法对80 km高度下的相割尖拱型弹头和抛物线型弹头进行了模拟分析。图12、图13、图14分别给出了不同外形弹头的密度、温度和速度分布云图，可以看出在相同的海拔高度、来流马赫数下，弹头外形的不同直接影响了激波形状。尖拱型弹头头部的激波较为显著，且对弹体表面的影响远强于钝头弹形，其驻点处附近密度较大，气流经过激波后逐渐减小，抛物线型弹头由于其钝头形状，只在弹头前部驻点处承受了很大的压力。

图15给出了不同外形弹头表面分布量计算结果，可以看出尖拱型弹头前部所承受的压力要高于钝头的抛物线型，这是由于其尖端的面积较小所造成的，在驻点后逐渐下降并开始低于钝头体的表面压力，与实际情况相符，二种弹头的压力系数在经过大约十几个自由程的长度后均逐渐趋于稳定。摩擦因数和热流通量也符合这一趋势。其中摩擦因数在弹头尾部出现小幅度的增加，这是因为流场右侧边界采用了真空边界条件，这和真实的环境存在差异，因此弹头尾部的模拟结果有偏差。用DSMC程序模拟得到的曲线在弹头的中部会有微小的上下起伏情况，这是由于DSMC程序固有的统计扰动所致，如果取样统计很好的话，这种扰动很小。但是这并不妨碍研究，总体的曲线趋势很明朗。现实中的高超声速飞行器一般都是钝头体，这也与实际情况下弹箭受力受热主要集中在钝头部分的现象吻合。

图12 不同外形弹头流场密度力分布云图

图13 不同外形弹头流场温度分布云图

图14 不同外形弹头流场速度分布云图

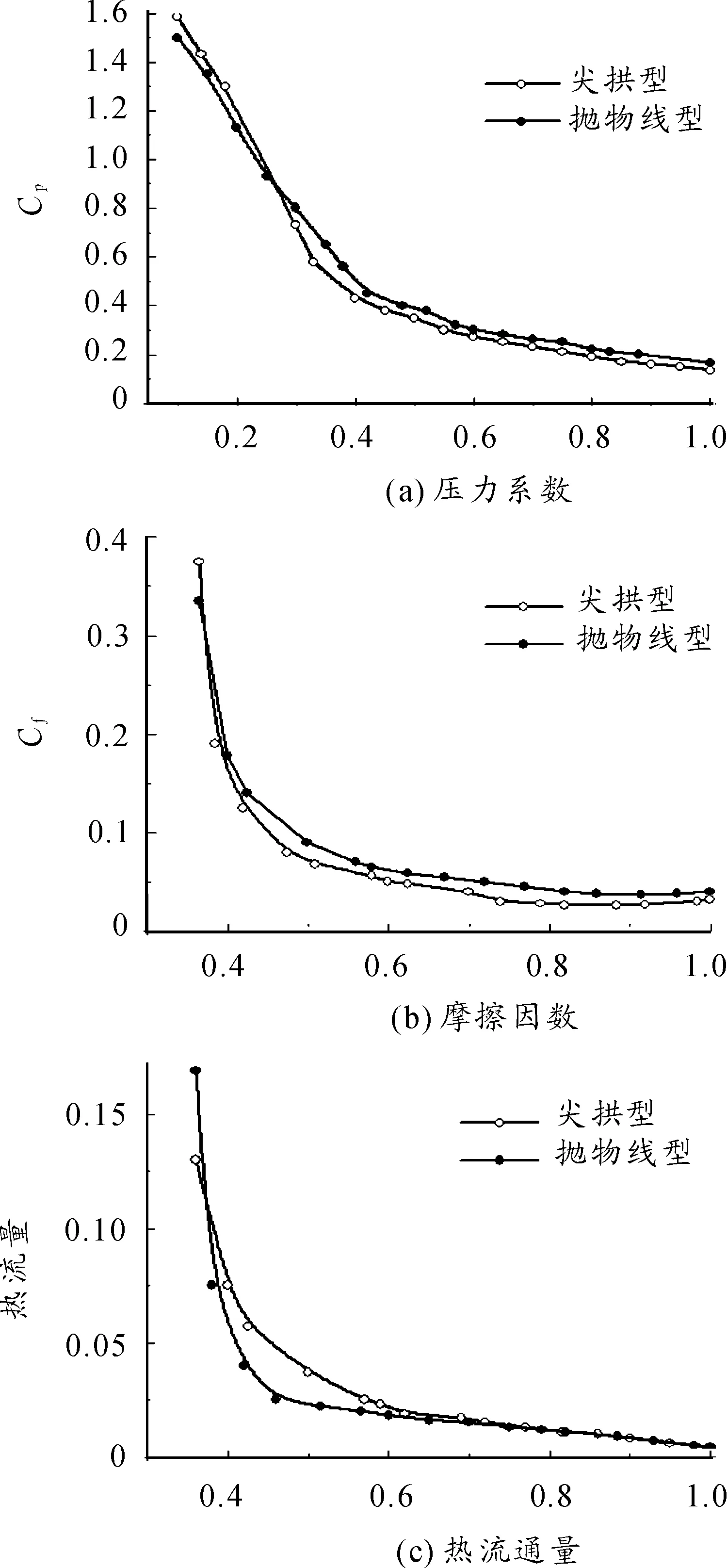
图15 不同外形弹头表面分布量计算结果

5 结论

本文利用DSMC技术研究高超声速稀薄气体流动模拟了不同高度下平板扰流流场，通过平板表面各计算值与文献数据的比较，验证了模拟方法和网格结构的有效性。而后对高空超音速弹丸的气动特性进行了DSMC模拟计算。建立其他外形的弹头气动模型并且使用自主编制的DSMC程序计算了不同外形弹头的气动力参数，模拟了高度变化对于稀薄气体流场的影响，得出以下结论：

随着海拔高度的增加，稀薄效应使得激波的厚度明显增厚，流场的压缩性减弱，但驻点处的温度依然最大，该部位的热流密度也最强，弹体表面的气体滑移影响减小，这是由于流动变得稀薄，分子间的碰撞频率明显降低，能量交换也不充分。

对于不同外形的弹头，尖拱型弹丸头部的激波尾部明显宽于抛物线型弹丸，直接表现为对弹头尾部流域的影响更为强烈，同时尖拱型弹丸前部的所受的压力与阻力均强于钝型弹头，但尾部的空气阻力效应稍弱，因而高超声速飞行器一般都采用钝头体。

[1] BIRD G A.Application of the DSMC method to the full shuttle geometry[J].AIAA,1990-1692.

[2] 李学东.稀薄气体高超声速流动的非结构DSMC并行化计算[J].科技回顾,2010,28(4):64-67.

[3] 李学东.非结构化网格下二维钝头体绕流DSMC数值模拟[C]//全国冲击动力学学术会议论文集.焦作:中国力学学会爆炸力学专业委员会冲击动力学专业组,2009.

[4] 黄海龙.稀薄气体中高超速圆柱绕流仿真研究[J].哈尔滨商业大学学报,2013,29(4):483-487.

[5] 蔡国飙.DSMC当地时间步长技术的理论发展[J].科学中国,2012,10(2):2750-2756.

[6] 叶友达.高空高速飞行器气动特性研究[J].力学进展,2009,39(4):387-397.

[7] BIRD G A.Molecular Gas Dynamics and the Direct Simulation of Gas Flow[M].Oxford:Clarendon Press,1994.

[8] AFTOSMIS M J.Solution Adaptive Cartesian Grid methods for Aerodynamic flow with complex geometries[C]//28th Computational fluid dynamics.[S.l.]:[s.n.],1997.

(责任编辑 周江川)

Numerical Simulation and Rarefied Gas Effect of Supersonic Warhead in High Flow Field

WANG Yong, WANG Xue-de, XU Guo-long

(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

A general computer program for numerical simulation of supersonic warhead in the high flow field by using DSMC simulation method with the Cartesian coordinate’s grid technique researching of hypersonic gas flow was worked out. To prove the validity of this method, the article made a contrast of the results with the data of theoretical model released related literature. Then, rarefied flow was simulated and calculated under different altitude, about the point arch warhead and other kinds of warheads in supersonic flow, the objective extending to the aerodynamic force calculation of different warhead shapes was used to study the effect of rarefied atmosphere. Analysis shows that with the elevation of altitude, the thickness of shock layer of the warhead increases because of rarefaction effect, and the compressibility of external flow field recedes, and the heat flux on the surface of warhead decreases. Compared with the pointed arch warhead, the pressure of blunt projectile is small in the stagnation point and is strong in the rear, which is in accord with the force law of blunt body of hypersonic aircrafts.

supersonic velocity; numerical simulation; rarefied flow; rarefaction effect

2016-05-23；

2016-06-20

江苏省青蓝工程资助项目

王勇(1991—)，男，硕士研究生,主要从事稀薄气体空气动力学研究。

10.11809/scbgxb2016.10.003

王勇，王学德，许国龙.超声速弹丸高空流场数值模拟与稀薄气体效应研究[J].兵器装备工程学报，2016(10):13-18.

format:WANG Yong, WANG Xue-de, XU Guo-long.Numerical Simulation and Rarefied Gas Effect of Supersonic Warhead in High Flow Field[J].Journal of Ordnance Equipment Engineering,2016(10):13-18.

TJ011.+2

A

2096-2304(2016)10-0013-06