基于混合改进型遗传算法的螺旋铣孔孔群加工路径优化研究

李忠群，郭文慧，王志康

（湖南工业大学 机械工程学院，湖南 株洲 412007）

基于混合改进型遗传算法的螺旋铣孔孔群加工路径优化研究

李忠群，郭文慧，王志康

（湖南工业大学 机械工程学院，湖南 株洲 412007）

在业已确定螺旋铣孔切削参数的前提下，孔群加工路径的优劣对加工效率有较大影响。研究TSP数学模型，应用混合改进遗传算法求解孔群加工路径优化模型，获得优化的加工路径。将3种算法基本遗传算法、蚁群算法和混合改进型遗传算法进行对比可知，本文提出的优化方法可有效缩短走刀时间。

遗传算法；螺旋铣孔；路径优化；蚁群算法

0　引言

螺旋铣孔是近年来新兴的一项柔性制孔技术，能用同一把刀具加工各种不同直径的孔［1-2］。螺旋铣孔工艺采用以铣代钻的方式，弥补了传统加工的不足，被广泛运用于高硬材料、钛合金及碳纤维增强复合材料（carbon fiber reinforced polymer/plastic，CFRP）的制孔中［3-6］。采用螺旋铣孔工艺加工孔群时［7］，由于各孔的相对位置及孔径的不同，刀具在孔群中的移动顺序将直接影响走刀时间。因此，有必要对走刀路径进行合理规划，使刀具空行程最短。通常，数控编程人员根据设计图纸人为确定加工路径，这种做法在孔数较少时尚能确保加工路径基本合理，但随着孔数目的增加，很难保证能获得合理的加工顺序。

孔群路径优化问题可以直接抽象为典型的旅行商问题（travel saleman problem，TSP）。旅行商问题是一个经典的组合优化问题［8］，具体描述如下：有一旅行商要访问n个城市，每个城市必须访问且只能访问一次，需要寻求到一条包含所有n个城市的最短访问路线［9-10］。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，因此它是一个NP（non-deterministic polynomial）完全问题。NP完全问题一般被认为是人们难以在有限的时间和空间内对问题求出最佳解的问题，利用非常规的求解技术求解是其常用的一种方法［11-12］。早期研究者使用精确算法如分枝定界法、线性规划法和动态规划法等来求解规模较小的旅行商问题，但运用到规模较大的问题中时，这些方法效果并不理想。因此，近来国内外学者重点采用智能算法诸如遗传算法、模拟退火算法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络算法等来求解该问题。

针对螺旋铣孔孔群加工路径优化问题，本文提出了一种混合改进型遗传算法。将刀具当作旅行商，待加工孔当作旅行商访问的城市，通过建立TSP数学模型并利用现代人工智能方法，进行参数模型化处理，最终获得最短加工路径，从而提高加工效率。

1　数学模型的建立

采用螺旋铣孔工艺加工孔群，其工作流程如下：刀具从作业起点开始，按照加工顺序依次对孔群进行加工，最后回到刀具起始位置。为减少问题的复杂性，对模型作如下假设。

1）刀具位置的控制精度能满足设计要求。

2）刀具在加工孔之间移动速度保持不变。

3）刀具在确定的铣削参数下进行孔群加工。

针对螺旋铣孔路径规划中加工零件和加工工艺两个对象，本文提出了一种解决路径规划的改进算法。在孔群加工顺序规划中，待加工孔的信息由孔的位置坐标（x， y）、孔径Dh和孔深h三个参数来描述，加工工艺参数由刀具直径Dt、主轴转速n、切向每齿进给量fzt和轴向每齿进给量fza来描述。在确定铣削条件下，设C=｛C1， C2， …， Cn｝是刀具在一次加工中所有待加工孔组成的孔群。确定一条经过各孔当且仅当一次的最短路径，其图论描述为：给定图G=（V， A），其中V为顶点集，A为各顶点相互连接组成的边集，已知各顶点间的边接距离，求一个n结点的带权完全图的最短Hamilton回路。定义加工过程刀具空行程的分布为：

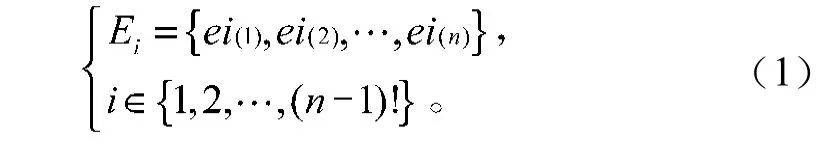
此时目标函数可简化为

2　混合改进型遗传算法

2.1经典遗传算法

经典遗传算法（classical genetic algorithm，CGA）是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法，其实质是种群搜索策略和种群个体间的信息交换，搜索不依赖于梯度信息。该算法是一种全局搜索算法，尤其适用于传统搜索算法难以解决的复杂和非线性问题。它的3个主要操作算子分别为选择算子、交叉算子和变异算子。遗传算法包括5个基本要素。

1）对参数进行编码。

2）设定初始种群大小。

3）设计适应度函数。

4）设计遗传操作。

5）设定控制参数（包括种群大小、最大进化代数、交叉率、变异率等）。

遗传算法的优点是使用简便、通用性强、实现简单，具有并行性和全搜索能力，缺点是易出现早熟和欺骗问题并且在快要接近最优解时会在最优解附近左右摆动［13］。

2.2蚁群算法

蚁群算法（ant colony optimization，ACO）是M.Dorigo等［14-15］根据蚂蚁群体在觅食过程中所体现出的智能行为提出的，通过模拟蚂蚁在寻找食物所体现出的寻优能力来解决现实中的优化问题。蚂蚁在寻找食物的过程中，会在沿途留下浓度不同的信息素（pheromone），路径越长信息素浓度越低，同时信息素会随着时间流逝而挥发，一条路径上走过的蚂蚁越多，则留下的信息素浓度越高，后来的蚂蚁可根据信息素浓度，以较大几率选择信息素较浓的路径。该过程是一种正反馈，并最终可以找到一条最优路径［16］。

蚁群算法的优点是它同时具有自适应、自组织、正向反馈和本质并行的特点，但其搜索时间较长，且容易受到因寻优过程中早期发现较好解的影响而陷入局部最优解，使搜索停滞。2.3混合改进型遗传算法

针对经典遗传算法和蚁群算法各自优缺点，本文将在遗传算法的基础上，通过适应度函数的修正和蚁群算法早期能发现较好初始种群等两方面来提高遗传算法的求解效率。在适应度函数构造上，将问题约束以动态方式合并到适应度函数中，得到一个具有变化惩罚项的适应度函数，用来指导遗传搜索；在初始种群生成方面，从蚁群算法早期产生的种群中选择初始解，构建更有效、更具有多样性的初始种群。

适应度函数的选择对能否快速、准确地找到最优解起着关键作用。针对旅行商问题，若目标函数为最小值问题，适应度函数可表示为

式中u（x）为个体的路径长度。

当初始群体中存在适应度超常（适应度值特别大或特别小）个体时，这些特殊个体可能会影响整个群体的发展方向，造成算法收敛于局部最优解，使局部最优解取代全局最优解。因此，限制超常个体的繁殖十分必要。此外，当迭代到后期算法逐渐收敛时，优劣个体间适应度值相差不明显，导致优良个体难以被继续优化，只能在最优解附近摇摆。基于上述考虑，本文对适应度值进行修正，即：

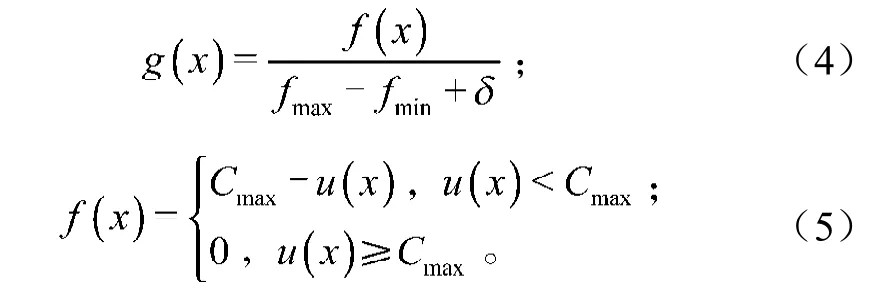
式中：f， g分别为修正前后的适应度值；

fmax， fmin分别为修正前适应度函数值的上下界（若该值未知，可用当前代或目前为止群体中最大/最小值来代替）；

δ为开区间（0， 1）内的一个正实数，可防止分母为零并增加遗传算法的随机性；

Cmax为当前代的最长路径。

图1是以原始适应度f（x）为自变量，新适应度函数值g（x）为因变量的一次函数关系图。图中，gmax， gmin分别为修正后适应度的最大、最小值。

由图1可知，随着fmax和fmin差值的增大，修正后的适应度函数的倾斜角变小，修正后的适应度值变化范围也会变小，从而可有效防止特殊个体影响整个群体造成局部收敛；若fmax和fmin的差值越小，则

越大，这样修正后的适应度值变化范围变大。在计算后期，拉开了群体中个体之间差距，避免了算法在最优解附近发生摆动。修正后的适应度可以依据群体适应度的值扩大或者缩小，变更选择压力。

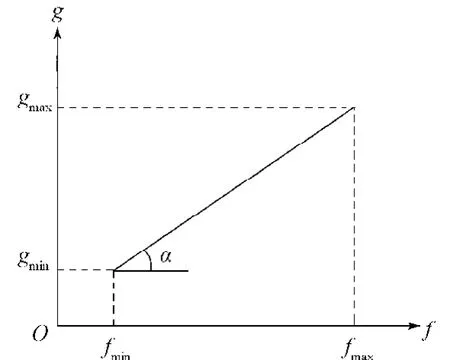
图1　适应度值的修正图Fig.1　Corrected of fitness values

在初始种群生成方面，本文利用蚁群算法得到遗传算法的初始种群。用m只蚂蚁对所有孔进行访问，选用不同的迭代次数作为停止条件，每只蚂蚁在不同迭代次数下走过的路径就表示一条基因（a0，a1，…， an），此基因表示此蚂蚁从a0出发经历a1， a2，…，an后再回到a0。为了提高初始种群的多样性，蚁群算法产生初始种群时，选用不同迭代次数下产生的基因。这样遗传算法在刚开始进行选择、交叉时就能以较大概率选择到路径最短的个体，以提高算法的效率和精度。

应用混合改进型遗传算法（improved hybrid genetic algorithm，IHGA）求解孔群加工顺序的流程图如图2所示。混合改进型遗传算法描述如下。

1）确定蚁群算法基本参数，通过改变最大迭代次数斜获取较优的蚂蚁序列群。

2）根据获得的优秀种群进行遗传交叉和变异操作获取符合要求的最优解。

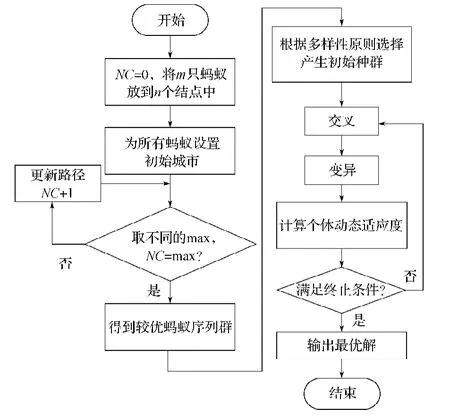
图2　混合改进型遗传算法流程图Fig.2　Flow chart of the improved hybrid genetic algorithm

3　孔群加工路径优化实例

在孔群加工中，孔的几何特征可表示为（x， y， Dh，h， num），其中x， y为孔的中心坐标，Dh为待加工孔的直径，h为孔深，num为孔的编号［17］。采用螺旋铣孔工艺对由30个孔组成的孔群进行加工，孔的参数如表1所示。位置分布如图3所示。

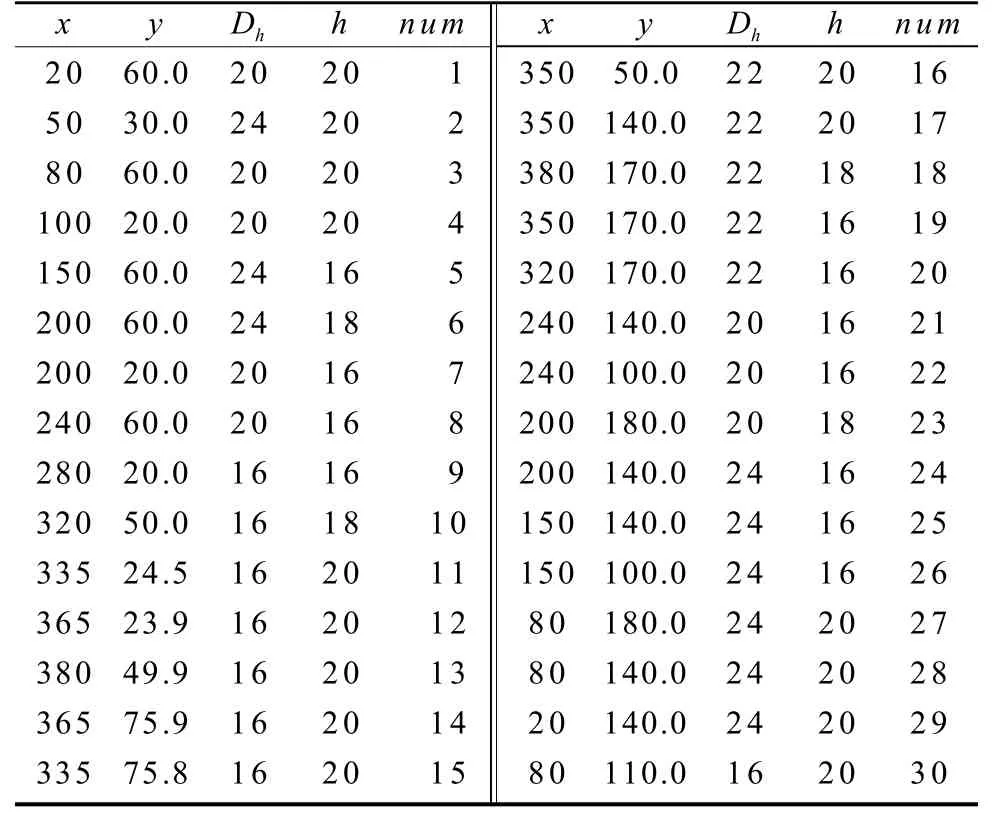
表1　30个孔的参数值表Table 1　Parameter value table of 30 holes mm

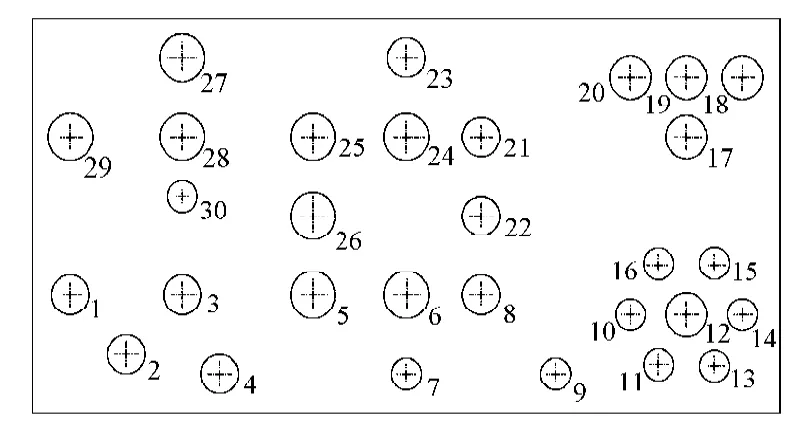
图3　某零件孔位置分布图Fig.3　Distribution of the component holes

本文分别利用基本遗传算法、蚁群算法和混合改进型遗传算法求解孔群的加工路径长度。计算平台为Pentium（R） Dual-Core CPU E5500 @ 2.80 GHz 1.87 GB，操作系统为Windows 7，仿真分析在MATLAB 7.0运行，仿真结果如表2所示。采用基本遗传算法和混合改进型遗传算法计算加工路径时，种群大小设定为100，交叉概率为0.8，变异概率为0.1；采用蚁群算法计算路径和产生初始种群时，设定蚂蚁个数m=31， 表征信息素重要程度的参数Alpha=1，表征启发式因子重要程度的参数Beta=5，信息素蒸发系数Rho=0.5，信息素增加强度系数Q=100。

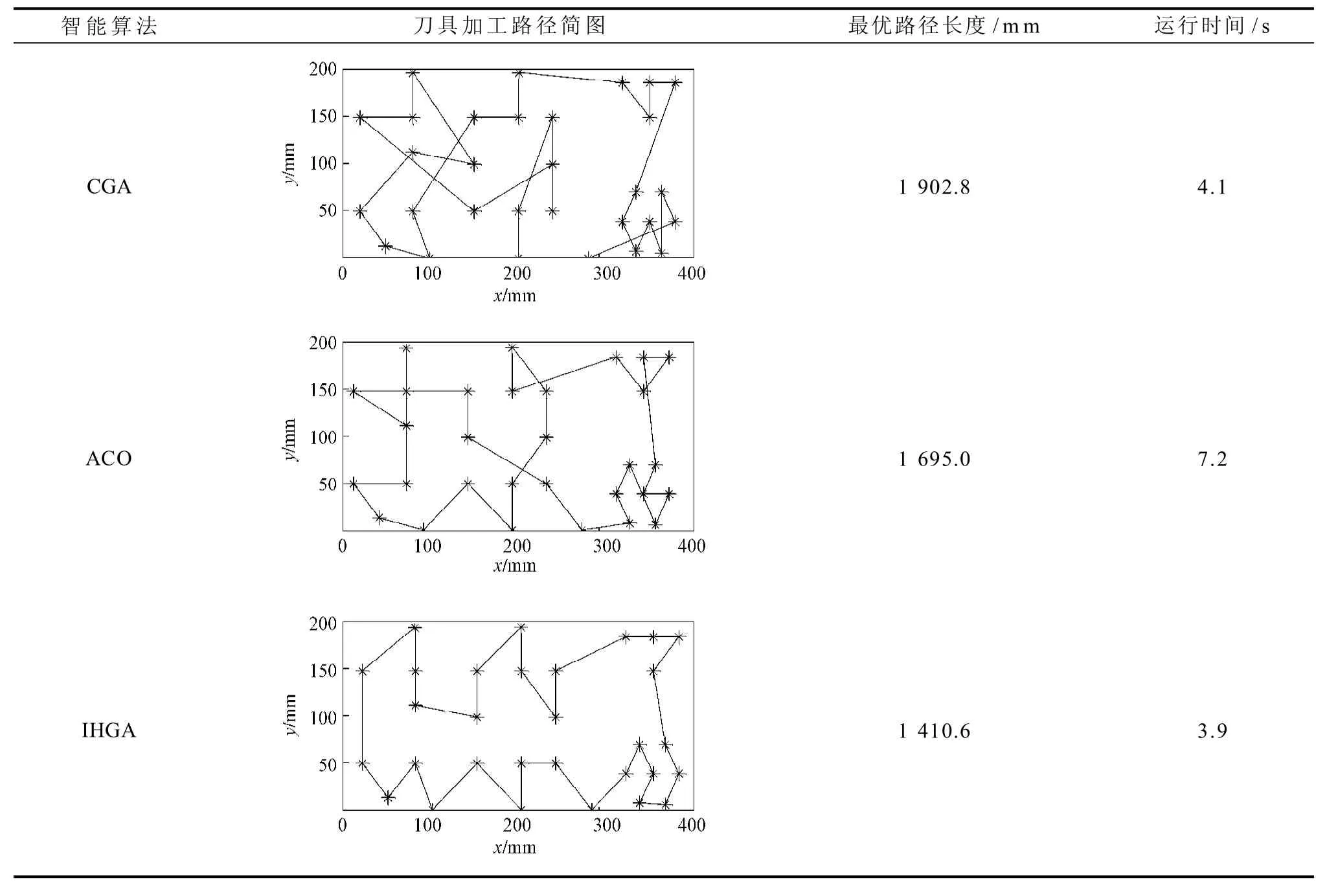
表2　基本遗传算法、蚁群算法和混合改进型遗传算法仿真结果对比表Table 2　Comparison table of simulation results of CGA， ACO and IHGA

由表2可知：在参数设置相同条件下，基本遗传算法、蚁群算法和混合改进型遗传算法求解同一孔群加工路径，得到的最短加工路径长度分别为：1 902.8，1 695.0， 1 410.6 mm，3种算法对应的运行时间分别为：4.1， 7.2， 3.9 s。加工路径长度方面，混合改进型遗传算法比基本遗传算法缩短路径长度26%，比蚁群算法缩短路径长度17%；程序运行时间方面，混合改进型遗传算法与经典遗传算法得到各自最优结果的运行时间大致相同，蚁群算法获得最优解的运行时间比2种遗传算法所需的时间都要长，此例中混合改进型遗传算法获得最优解的时间比蚁群算法获得最优解的时间节省约46%，混合改进型遗传算法在整体上以更短的执行时间以及有限的迭代次数获得最短路径。混合改进型遗传算法放弃了基本遗传算法中随机产生初始种群的方法，利用蚁群算法具有正反馈、自适应的特点，从蚁群算法中蚂蚁已走过的路径中选择生成初始种群，在保证了初始种群高质量的同时也避免了部分初始解超常导致算法局部收敛的情况。此外，混合改进型遗传算法在计算由交叉、变异后产生的新个体的适应度时，构建具有变化惩罚项的适应度函数来避免算法在运算后期时，求解结果在最优解附近摆动而始终无法逼近最优解的情况，提高了算法效率。

4　结语

1） 考虑遗传算法中欺骗问题和初始种群的有效性，构建了具有变化惩罚项的适应度函数和新的初始种群产生方法。

2） 应用混合改进型遗传算法求解孔群加工路径优化模型，获得优化的加工路径。对比优化前后的路径长度发现，本文提出的优化方法可有效缩短走刀时间。

3） 混合改进型遗传算法仿真结果，可为螺旋铣孔工艺加工孔群实际工程应用提供理论指导。

［1］李忠群，郑敏，王鑫.螺旋铣孔技术研究进展［J］.湖南工业大学学报，2013，27（1）：38-42.LI Zhongqun，ZHENG Min，WANG Xin.Research Progress of Helical Milling Operation［J］.Journal of Hunan University of Technology，2013，27（1）：38-42.

［2］BRINKSMEIER E，FANGMANN S，MEYER I.Orbital Drilling Kinematics［J］.Production Engineering，2008，2（3）：277-283.

［3］DENKENA B，BOEHNKE D，DEGE J H.Helical Milling of CFRP Titanium Layer Compounds［J］.Cirp Journal of Manufacturing Science & Technology，2008，1（2）：64-69.

［4］李忠群，夏磊，彭岳荣，等.基于实验模态分析的铣削加工系统动力学特性参数测试与分析［J］.湖南工业大学学报，2015，29（4）：6-9.LI Zhongqun，XIA Lei，PENG Yuerong，et al.Dynamic Characteristics Test and Analysis of Milling System Based on Expermental Modal Analysis［J］.Journal of Hunan University of Technology，2015，29 （4）：6-9.

［5］李忠群，彭岳荣，夏磊，等.基于改进欧拉法的铣削稳定性半解析法预测［J］.湖南工业大学学报，2015，29（6）：6-10.LI Zhongqun，PENG Yuerong，XIA Lei，et al.Semi-Analytical Method for Milling Process Stability Prediction Based on Improved Euler Method［J］.Journal of Hunan University of Technology，2015，29（6）：6-10.

［6］李忠群，董亚峰，夏磊，等.考虑过程阻尼的切削稳定性建模与仿真分析［J］.湖南工业大学学报，2014，28（6）：23-26.LI Zhongqun， DONG Yafeng，XIA Lei，et al.Modeling and Simulation on Cutting Process Stability Considering Process Damping［J］.Journal of Hunan University of Technology，2014，28（6）：23-26.

［7］BULLNHEIMERB，KOTSISG，STRAUC.Parallelization Strategies for the Ant System［J］.High Performance Algorithms and Software in Nonlinear Optimization，1998，24：87-100.

［8］KHAN W A，HAYHURST D R，CANNINGS C.Determination of Optimal Path Under Approach and Exit Constraints［J］.European Journal of Operational Research，1999，117（2）：310-325.

［9］LIN W，DELGADO-FRIAS J G，GAUSE D C，et al.Hybrid Newton-Raphson Genetic Algorithm for the Traveling Salesman Problem［J］.Cybernetics and Systems，1995，26（4）：387-412.

［10］MANIEZZO V，COLORNI A.The Ant System Applied to the Quadratic Assignment Problem［C］//IEEE Transactions on Knowledge and Data Engineering.［S.l.］：IEEE，1999，11（5）：769-778.

［11］Holland J H.Adaptation in Natural and Artificial Systems：An Introductory Analysis With Applications to Biology，Control， and Artificial Intelligence［J］.Control & Artificial Intelligence University of Michigan Press，1975，6（2）：126-137.

［12］COFFMAN E G，GAREY M R，JOHNSON D S.Approximation Algorithms for Bin Packing：A Survey［C］// Approximation algorithms for NP-Hard Problems.［S.l.］：PWS Publishing Co.，1996：46-93.

［13］MAK K L，WONG Y S，WANG X X.An Adaptive Genetic Algorithm for Manufacturing Cell Formation［J］.International Journal of Advanced Manufacturing Technology，2000，16（7）：491-497.

［14］DORIGO M，MANIEZZO V，COLORNI A.Ant System：Optimization by a Colony of Cooperating Agents［J］.IEEE Transactions on Systems， Man， and Cybernetics：Part B（Cybernetics），1996，26（1）：29-41.

［15］DORIGO M，GAMBARDELLA L M.Ant Colony System：A Cooperative Learning Approach to the Traveling Salesman Problem［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：53-66.

［16］DORIGO M，GAMBARDELLA L M.Ant Colonies for the Travelling Salesman Problem［J］.Bio Systems，1997，43（2）：73-81.

［17］王鑫.基于加工特征的机床关键零件高效数控加工切削参数优化技术研究［D］.株洲：湖南工业大学，2014.WANG Xin.Machining Features Based on Cutting Conditions Optimization for High Performance CNC Machining of Key Machine Parts［D］.Zhuzhou：Journal of Hunan University of Technology，2014.

（责任编辑：邓彬）

On the Optimized Machining Path for Group Holes Realized by Helical Milling Based on an Improved Hybrid Genetic Algorithm

LI Zhongqun，GUO Wenhui，WANG Zhikang
（School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007）

A great influence will be exerted on the machining efficiency by the optimization degree of machining paths for group holes.An optimized processing path， based on a research of TPS mathematical models， can be achieved by the application of an improved hybrid genetic algorithm to the solution of the optimization of holes machining paths.A comparison between the classical genetic algorithm， the ant colony algorithm and an improved hybrid genetic algorithm shows that the proposed optimized method helps to improve the machining efficiency by greatly shortening the machining time.

genetic algorithm；helical milling；path optimization；ant colony algorithm

TG54 ；TH313

A

1673-9833（2016）04-0027-05

10.3969/j.issn.1673-9833.2016.04.006

2016-05-30

国家科技重大专项基金资助项目（2012ZX04011-011）

李忠群（1966-），男，湖南永州人，湖南工业大学教授，博士，主要从事数字化制造与装备技术，虚拟制造方面的研究，E-mail：zhqunli@163.com

郭文慧（1990-），男，山西大同人，湖南工业大学硕士生，主要研究方向为数字化制造与装备技术，E-mail：guowenhuizongwu@163.com