让“数”与“形”和谐交融
□江苏省常熟市元和小学 张志英
让“数”与“形”和谐交融
□江苏省常熟市元和小学张志英
数学是什么?新课程标准指出“数学是研究数量关系和空间形式的科学”。“数量关系”就是数,“空间形式”就是形,数和形的关系十分密切。而反思我们的教学却常常过早地把数与形割裂开,我们老师主动运用意识淡薄,运用范围狭窄,体现方式单一。所以在教学中我们应有意识地把数和形结合起来,适时渗透数形结合的思想,让“数”与“形”和谐交融,从而达到事半功倍的效果。
一、渗透数形结合思想,利用数形结合认识数
建构主义认为学生学习活动的本质是:学习并非对于教师所授予的知识的被动接受,而是学习者以自身已有的知识和经验为基础的主动建构过程。数的认识对于学生而言是比较枯燥、抽象的数学概念,学生的学习以直观形象思维为主,通过数形结合,给学生大量“形”的支撑,能使比较抽象的数的认识转化为清晰、具体的事物,学生容易掌握和理解。
例如在“千以内数的认识”中,我们利用学具方块计数卡形象直观地将计数单位之间的“十进制关系”呈现了出来。一开始借助小正方体数数,经历数数,感受到不同的情况下可以采取不同的数数方法,同时直观感受一十、一百、一千的表象,知道一十是1列,一百拼成1片,一千成了1个大正方体,为进一步理解1000以内数的组成打下基础。同时认识计数单位百、千,并感悟到10个一是一十,10个十是一百,10个百是一千的十进关系。

图1
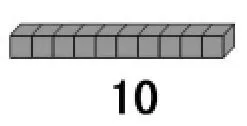
图2
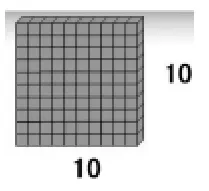
图3
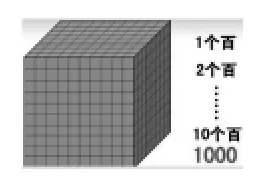
图4
实践证明:在认识数的教学中运用数形结合,向学生提供大量的“形”的材料,把抽象的数概念直观化,激发了学生学习数学的兴趣,达到了事半功倍的效果。
二、渗透数形结合思想,利用数形结合来计算
小学数学内容中,有相当部分的内容是计算问题,计算教学要引导学生理解算理,正所谓“知其然,知其所以然”。这时运用数形结合是帮助学生正确理解算理的一种很好的方式,让学生对算理的理解更加透彻。


利用数形结合的方法,学生表象清晰,记忆深刻,对算理理解透彻,事实上也是形象思维与抽象思维协同应用的一种过程,其教学效果显而易见。
三、渗透数形结合思想,利用数形结合找规律
数学是模式的科学,是思维的体操。学生学习数学的过程应该是通过数学思维活动不断探索发现数学规律、应用数学规律解决问题的过程。而小学生的思维发展特点是从具体形象思维逐步向抽象逻辑思维过渡,但很大程度上仍具有具体形象性。通过数与形的有机结合,从而把形象思维和抽象思维有机结合起来,从而让学生多角度、多层次的思考问题。
例如“点阵中的规律”(图5)通过数形结合,借助“形”的生动和直观认识“数”,观察前3个点阵图,学生整体上了解图形的圆点排列特点,然后通过想象点阵图4的样子和圆点个数,从而做出大胆的猜想、合理的假设,训练学生的数学直觉思维能力。然后重点探索第5个点阵图(图6)的规律,通过不同角度的思考,和相应的数学算式结合起来,发现结果都是25,从而沟通知识之间的联系,让学生去探索、探讨、发现,得出图7。这样的教学以“数”解“形”,使学生更准确地把握“形”,将已有的思维方式大跨度地迁移,进而发现蕴含在图形中的数学规律。

图5

图6

图7
我们的教学应该注重在数学思想方法引领下学生自主探索数学规律。学生只有经历这样的探索过程,在获取知识和技能的同时,数学思想方法才能积沉、凝聚在数学知识结论上,从而使知识具有更大的智慧价值。
四、渗透数形结合思想,利用数形结合解决实际问题
运用数形结合有时能使数量之间的内在联系变得比较直观,成为解决问题的有效方法之一。在分析问题的过程中,注意把数和形结合起来考察,根据问题的具体情形,把图形的问题转化为数量关系的问题,或者把数量关系的问题转化为图形的问题,使复杂问题简单化,抽象问题具体化,化难为易,从而提高学生的思维能力。
例如教学分数实际问题时,引导学生学会画线段图,线段图是理解抽象数量关系的形象化、视觉化的工具。借助线段图,使已知条件之间、条件和问题之间的关系更加清楚,变“看不见”为“看得见”,从而直观形象地理解抽象的数量关系,还能进一步明确和拓宽解题思路,发展学生的思维。
以上所述只是“数与代数”领域教学中渗透数形结合思想的几个例子,“数形结合思想方法”包含“以形助数”和“以数辅形”两大方面,只要我们学会做个有心人,以数形结合的观点钻研教材,挖掘教材,就会发现数形结合的很多渗透点。让我们将渗透数形结合思想的教学进行到底,让“数”与“形”和谐交融,使这种思想成为学生运用自如的思想观念和思维工具,从而提高学生的数学修养与解题能力。

