基于模糊层次分析法的雷达导引头干扰效能评估*
杨远志,王星,程嗣怡,周东青
(空军工程大学航空航天工程学院,西安710038)
基于模糊层次分析法的雷达导引头干扰效能评估*
杨远志,王星,程嗣怡,周东青
(空军工程大学航空航天工程学院,西安710038)
为评估对主动雷达导引头的干扰效能,结合导引头工作原理和功能特性,运用模糊数学理论,构建了对雷达导引头干扰效能进行评估的指标体系,建立了二级模糊评判模型,采用正态分布形式构造隶属函数,并利用指数标度的层次分析法(AHP)确定各因素的权重,使得判断矩阵的一致性指标得到改善,实现对雷达导引头的量化评估。最后选择噪声干扰为例进行模糊综合评判,实例分析结果表明该雷达导引头干扰效能模糊评判模型具有实用性,其评估结果可为干扰措施的选择提供参考。
雷达导引头,干扰效能评估,指数标度,模糊层次分析法
0 引言
随着科技的发展,空空导弹武器装备性能得以不断提高,主动雷达制导型空空导弹已成为战机的主要威胁。在末制导阶段的电子干扰对抗,是直接决定战机生存安全的关键。
对雷达导引头干扰效能的评估实质上是基于干扰性能与多个指标的依赖关系,建立多个指标与干扰性能的映射关系,进而可以利用各个评估指标的量化值得到最终的评估结果[1]。但是这种关系一般情况下具有很强的不确定性和模糊性,难以用明确的数学表达式将其表示出来。同时,影响干扰效能的因素很多,各因素起到的作用以及因素之间的关系同样具有模糊性。模糊层次分析法(FAHP)是将层次分析法和模糊综合评判法进行有机融合,用层次分析法确定各因素权重,用模糊评判法确定各方案指标,可以处理用其他方法无法处理的模糊信息[2],提高决策的准确性和效率[3]。在对导引头干扰效能进行模糊综合评判时,关键在于运用AHP确定指标权重,而指数标度AHP具有一致性好、人为主观性低等优点[4-5],可以对指标权重作出更加合理的判定。
因此,本文将指数标度AHP和模糊综合评判法相结合,建立导引头干扰效能评估指标体系以及模糊综合评判模型,构建一种合理、科学的导引头干扰效能评估方法。
1 建立评估指标体系
建立科学合理的评估指标体系,是评估研究中关键的一环,它是进行评估的基础,没有评估指标体系,评估工作就无法进行。
本文从主动雷达导引头的固有抗干扰能力[6]及工作过程进行分析,建立了如图1所示的雷达导引头干扰效能评估指标体系。
1.1工作体制抗干扰因子
采用专家打分的评估方法对其量化。经过分析建立的工作体制抗干扰因子模型为:其中,ωi取值为0或1,某型雷达采用了该体制,则ωi=1,否则ωi=0;μi为第i种工作体制相对导引头抗干扰性能的贡献度。
式中,EJ介于0~1之间,且取值越大,干扰效果越好。

表1 工作体制相对导引头抗干扰性能的贡献度
1.2技术措施抗干扰因子
根据专家打分,目前雷达广泛采用的12种抗干扰措施及对导引头抗干扰能力的贡献度如表2所示。

表2 抗干扰措施对雷达抗干扰能力的贡献度
在实际应用中,采取多种技术措施后,导引头的抗干扰能力近似于各自抗干扰能力的和值,因此,可建立技术措施抗干扰因子模型为:
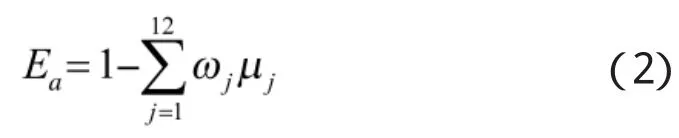
其中,ωj取值为0或1,某型雷达采用了该体制,则ωj=1,否则ωj=0;μj为第j种抗干扰措施对导引头抗干扰性能的贡献度。
式中,Ea介于0~1之间,且取值越大,干扰效果越好。
1.3自卫距离
自卫距离是干扰对导引头有效作用的最小干扰距离,计算公式如下[7]:
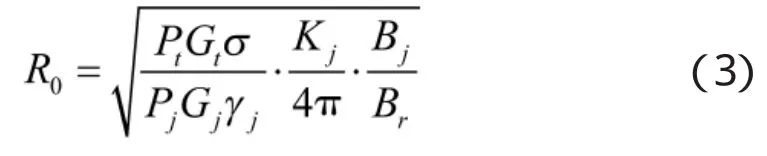
式中,Pj为干扰机功率,Gj干扰机天线增益,Br为导引头接收机带宽,Pt为导引头发射机功率,Gt为导引头天线增益,σ为目标散射截面积,Bj为干扰接收机带宽,γj为干扰与雷达信号的极化失配系数,Kj为产生有效干扰所需的最小压制系数,对导引头干扰有效一般要求Kj≥10。
用导引头最大探测距离Rmax的损失状况来衡量干扰效能,定义最大探测距离损失度Er,作为自卫距离的归一化指标。
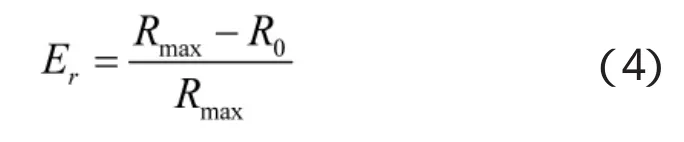
式中,Er介于0~1之间,取值越大,干扰效果越好。
1.4干扰作用因子
干扰作用因子Fp主要从功率层面来考虑干扰效果,用来描述雷达受到干扰后和未受到干扰时其输出端干信比的比值,即:

本文取Fp≥2Kj时,评价结果为“很好”;Fp≤Kj/2时,评价结果为“很差”。对其进行归一化处理,得到下式:
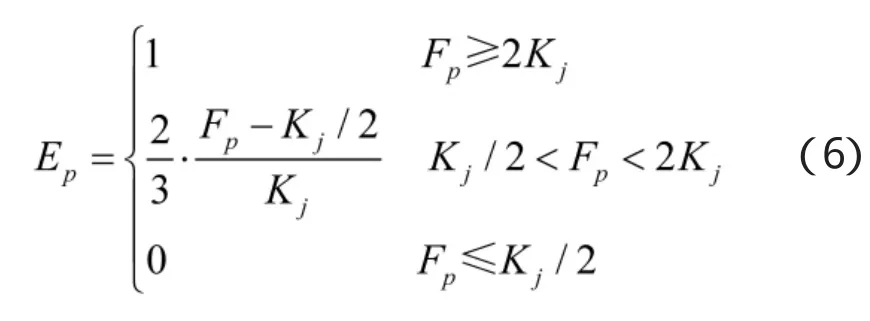
上式表明归一化因子Ep越大,干扰后的干信比越大,则干扰效果越好。
1.5有效截获时间
有效截获时间是指从导引头开始工作到真实目标被雷达系统发现的时间间隔Tc。比较干扰前后截获时间的变化,可定义截获时间的归一化指标Et为:

式中,Tc'是被干扰后导引头截获时间。同样Et在0~1之间变化,取值越大,干扰效果越好。
1.6有效跟踪概率
有效跟踪是指导弹导引头输出的测量信息结果,能够引导导弹完成正常的跟踪引导过程,而不产生较大误差的工作状态。在某种典型空战对抗下进行N次仿真,如果导引头只有M次建立了有效跟踪,则得到干扰下导引头的有效跟踪概率为:

此时P越小,干扰效果越好。为使该指标与上述评估方式统一,定义有效跟踪概率的归一化指标为:

式中,Ec介于0~1之间,且取值越大,干扰效果越好。
1.7距离(速度、角度)跟踪误差
导引头作为制导雷达,跟踪测量误差是十分重要的参数指标。对于压制性干扰而言,由噪声引起的某一跟踪误差σj与干信比具有如下关系[8]:
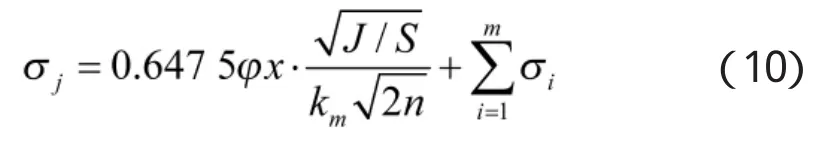
式中,φ为平滑系数,x为被测参数,km为系数,n为测量次数,J/S为干信比;σ1~σm是系统测量误差。根据受到干扰后,接收机干信比的变化情况,可以分别得到干扰前后跟踪误差的变化结果。
以误差增大倍数来衡量干扰效果,得到跟踪误差的归一化评估指标为:
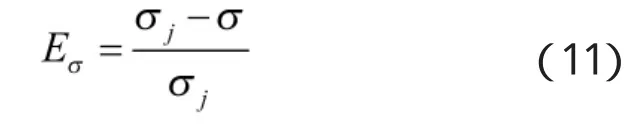
式中,Eσ介于0~1之间,取值越大,干扰效果越好。
2 建立模糊综合评判模型
对雷达导引头干扰效能进行评估,是模糊数学在工程评判上的应用。其具体的建模过程如下:首先建立影响导引头干扰效能的因素集u,在对导引头的干扰效能评估中,因素集就是评估的指标体系;其次确定评价集,用诸如“很好、好、一般、差、很差”的一组模糊语言评价干扰效果的优劣;接着确定隶属函数,计算得到各指标对应的隶属度,继而得到相对于上层元素的隶属度矩阵R。在进行上述步骤的同时,运用指数标度AHP构造层次结构以及判断矩阵,并得到各指标的权重向量w。最后利用综合评判B=W。R得出综合评判结果(。为模糊算子)。具体的模糊综合评判算法流程见图2所示。
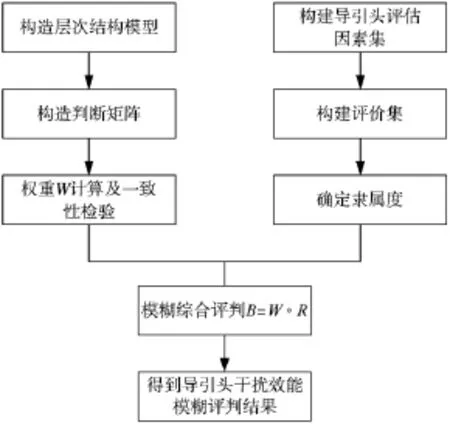
图2 模糊综合评判算法流程图
2.1建立因素集
根据图1建立的评估指标体系,可以确定因素集为u={u1,u2,u3},u1={u11,u12},u2={u21,u22,u23},u3= {u31,u32,u33,u34}。
2.2确定评价集
评价集是对评价对象可能作出的评价结果所组成的结果,可表示为V={v1,v2,…,vq},其中vp(p=1,2,…,q)是可能作出的第p个结果。本文把干扰效果划分为5个等级。评判集为V={很好,好,一般,差,很差}。
2.3确定隶属函数
隶属函数是用于表征模糊集合的数学工具。在干扰效能评估中,隶属函数的确定一般要根据产生干扰效能的原理,结合其数学表达式或作用方程,选择能够合理反映因素对干扰效能影响程度的隶属函数。常用隶属函数分布主要类型有:矩形分布、抛物型分布、梯形及半梯形分布、正态分布、柯西分布、岭形分布等。为研究规则的完备性、相容性,获取更多的评估效果,本文的隶属函数选择为正态分布型[9],即:
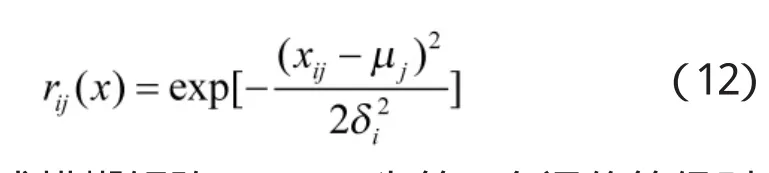
式中,rij组成模糊矩阵R,μj、σj为第j个评价等级对应的分布参数。同时对两端处的隶属函数用常数1作出修正,根据多位专家经验知识确定μj,σj取值,得到参数设置如表3所示:

表3 参数[μj,σj]取值
2.4指数标度AHP确定因素权重
权重用于描述各指标相对于上级评价指标的相对重要程度。一般情况下,各个因素在评判中具有不同的重要性,对各个因素μi对应地分配不同的权重w={w1,w2,…,wn},从而得权重集。指数标度层次分析法是采用指数标度量化判断矩阵,具有一致性好、人为主观性低等优点[10],采用这种方法对于导引头干扰效能的评估能够起到更为客观的效果。因此,本文采用指数标度AHP确定因素权重。
具体的权重标度[11]划分见表4。

表4 改进指数标度
运用层次分析法进行权重确定时,其具体构权步骤为:
①依据指数标度,构造评定指标两两判断矩阵A=(aij)n×n,aij为评定指标i与指标j重要性关系标度值,按表2取值,n为评定指标的个数。
②通过求解矩阵A的特征方程Aλ=Wλ,计算最大特征值λmax和对应的特征向量W={w1,w2,…,wn}T,即得到权重向量W。
③一致性检验。在构造两两判断矩阵时,由于客观事物的复杂性以及人类判断能力的差别,构造的判断矩阵难以达到完全一致,可能会出现A比B重要、B比C重要、C比A重要的错误结果。因此,需要对所构造的判断矩阵进行随机一致性检验[12]。具体步骤如下:
a.计算一致性指标C.I.

b.查表得平均随机一致性指标R.I.
对应不同的矩阵维数,需要用不同修正因子R. I.对C.I.进行修正。

表5 一致性指标R.I.取值
表5中,对于1维、2维矩阵,总是完全一致的,即C.R.=0,不需要一致性检验。
c.计算一致性比例C.R.

一般认为当C.R.<0.1时,矩阵A符合一致性要求;当C.R.>0.1时,矩阵A不符合一致性要求,则必须对矩阵A作出调整后,再重新进行一致性检验,直到矩阵A符合一致性要求为止。
2.5模糊综合算法
根据上述计算结果,可以得到模糊综合评判集

其中,。为模糊算子,常用的算子有极大极小型、乘积取大型、加权平均型等。
对于雷达导引头来说,对它的干扰效能是所有因素的一个综合体现,因此,采用加权平均型算子M(。,)作为计算该系统的模糊算子。
2.6评判结果处理
确定最终评判结果,本文采用最大隶属度方法[13]:取模糊综合评判集B=[b1,b2,b3,…,bn]中最大评判指标记为b0,与b0相应的评价结果为最终评判的结果。
3 实例计算
以噪声调频干扰为例,假设一种单脉冲主动雷达导引头采取了HOJ、恒虚警、MTD 3种抗干扰技术,其雷达天线发射功率300 W,增益30 dB,中频带宽4 MHz,工作比d=0.01,对RCS为5 m2的目标作用距离为20 km;机载自卫干扰机功率50 W,天线增益10dB,噪声干扰带宽40MHz,极化失配系数3dB。根据上述计算得自卫距离1 459 m,在弹目距离为10km时,噪声进入接收端的干信比为9.8dB。
采用指数标度层次分析法,综合各专家评估意见,建立判断矩阵:

进行一致性检验,最终得到各指标的权重见表6所示。
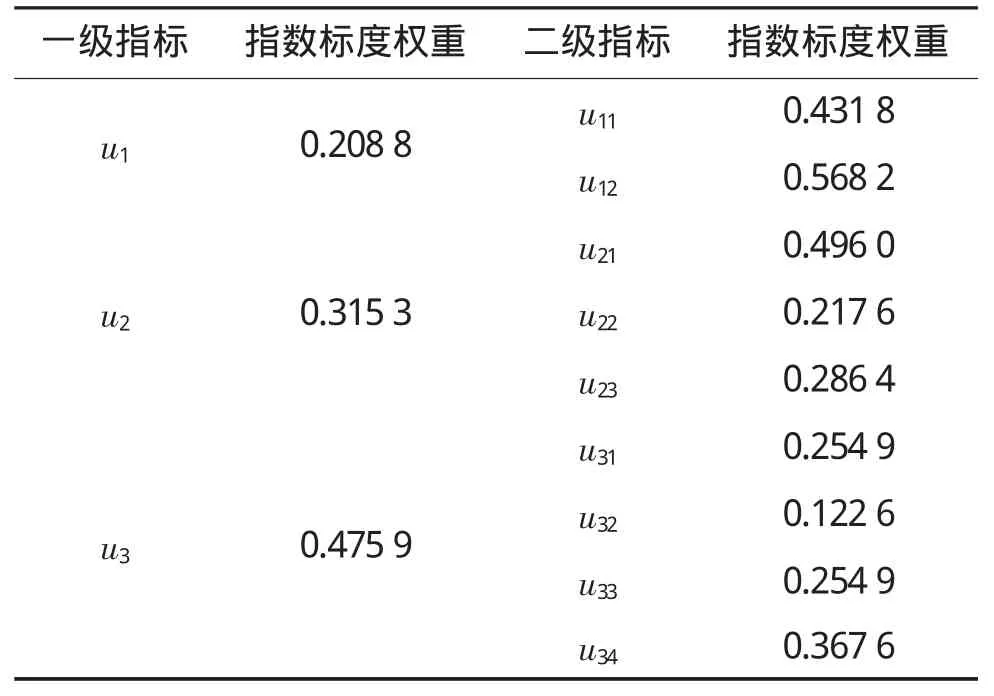
表6 各指标因素的权重
根据上述模糊评估方法中隶属函数、评价指标得到对雷达导引头干扰效能评估的一级模糊矩阵为:
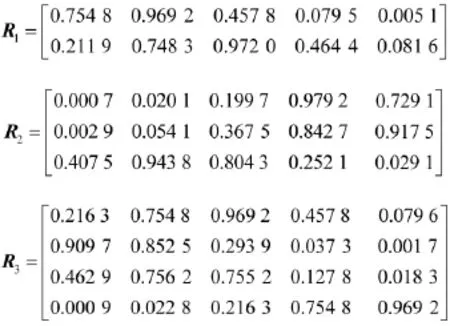
R1是对导引头固有抗干扰能力干扰效能的模糊矩阵,R2是对截获过程干扰效能模糊矩阵,R3是对跟踪过程干扰效能模糊矩阵。采用加权平均型算子进行评估计算,由综合评判模型Bi=Wi。Ri,得出一级评判结果为:

归一化结果为:

则二级模糊矩阵为:

由B=W。R,得二级评判结果为:
B={0.1195,0.2273,0.2290,0.2312,0.1729}
对评判结果的处理采用最大隶属度方法,由二级评判结果可知,对导引头固有抗干扰能力干扰效果为“好”,截获性能干扰效果为“差”,对跟踪性能干扰效果为“一般”;由一级评判结果可知,对导引头整体干扰效能为“差”。
4 结论
本文通过对雷达导引头工作特性的分析,建立了雷达导引头干扰效能评估的指标体系,并将指数标度AHP与模糊综合评判相结合,得到定量评估导引头干扰效能的模糊综合评判模型。最后以噪声调频干扰为例计算得到评估结果,验证了模型的有效性。本模型同样可以适用于其他干扰样式对导引头的干扰效能评估问题,因此,本文的干扰评估方法具有通用性。
[1]魏保华,孟晨,范书义,等.基于变权模糊综合评判的雷达抗干扰性能评估[J].现代雷达,2010,32(9):15-18.
[2]谭维锴,郭爱煌,钱业青.基于模糊层次分析的小小区性能评估[J].系统工程与电子技术,2014,36(8):1651-1655.
[3]DEHGHANIAN P,FOTUHI F M,BAGHERIi S S,et al. Critical component identification in reliability centered asset managementofpowerdistributionsystemsviafuzzy AHP[J]. IEEE SystemJournal,2012,6(4):593-602.
[4]沈继红,付肖燕,赵玉新.感觉判断矩阵的一致性改进[J].哈尔滨工程大学学报,2011,32(3):395-399.
[5]王剑钦,张伟华,马润年.基于指数标度和灰色理论的空军通信能力评估模型[J].空军工程大学学报(自然科学版),2009,10(5):64-69.
[6]杜海文,孟领坡,马洪斌.防空导弹制导雷达综合抗干扰能力评估[J].火力与指挥控制,2004,29(5):54-61.
[7]王星.航空电子对抗原理[M].北京:国防工业出版社,2008.
[8]潘超.雷达抗干扰效能评估准则与方法研究[D].成都:电子科技大学,2003.
[9]周颖,王雪松,王国玉.基于战区弹道导弹突防的雷达干扰效果模糊评估[J].系统工程与电子技术,2003,25(7):807-809.
[10]吕跃进,张维.指数标度在AHP标度系统中的重要作用[J].系统工程学报,2003,18(5):452-456.
[11]孙东生,朱懿,周水兴.基于指数标度的层次分析法在桥梁评定中的应用[J].重庆交通大学学报(自然科学版),2010,29(6):867-870.
[12]王经商,吴华,程嗣怡,等.GAHP的机载雷达射频隐身性能评估[J].空军工程大学学报(自然科学版),2016,17(2):37-41.
[13]王国玉,汪连栋.雷达电子战系统数学仿真与评估[M].北京:国防工业出版社,2002.
Jamming Effectiveness Evaluation of Radar Seeker Based on Fuzzy Analytical Hierarchy Process
YANG Yuan-zhi,WANG Xing,CHENG Si-yi,ZHOU Dong-qing
(School of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China)
In order to evaluate jamming effectiveness of radar seeker,according to the function characteristics and principle of radar seeker,using fuzzy mathematics theory,this paper builds the evaluation index system of the radar seeker and two-stage fuzzy combined evaluation model. Membership function is established with normal distribution,and the weight of the index system is set up with AHP with index scale which improves the concordance index of judgment matrix and realizes quantized evaluation of radar seeker.Finally,noise jamming is chosen as an example to verity the model,the example shows the effectiveness of the model and the evaluation results can provides reference of choosing jamming measures.
radar seeker,jamming effectiveness evaluation,index scale,fuzzy analytical hierarchy process
TN97
A
1002-0640(2016)10-0010-05
2015-08-18
2015-09-16
陕西省自然科学基金资助项目(2012JQ8019)
杨远志(1991-),男,四川绵竹人,硕士研究生。研究方向:电子对抗理论与技术。

