基于微多普勒特征的欺骗干扰识别*
杨少奇,田波,赵双,贺思三
(空军工程大学防空反导学院,西安710051)
基于微多普勒特征的欺骗干扰识别*
杨少奇,田波,赵双,贺思三
(空军工程大学防空反导学院,西安710051)
为了提高雷达的抗干扰能力,提出了一种基于微多普勒特征的欺骗干扰识别方法,为雷达选择抗干扰措施提供了先验知识。首先建立了目标回波和干扰信号的数学模型,分析了二者微多普勒频率的差异。其次利用Viterbi算法和FFT谱分析对信号的特征参数进行了提取。最后,定义了识别目标和干扰的特征因子,并根据特征因子设定阈值对目标回波和欺骗干扰进行识别。仿真结果验证了算法的正确性和稳定性,与理论分析一致,表明该方法能够在较低的信噪比环境下对欺骗干扰进行检测识别。
微多普勒,Viterbi,特征提取,干扰识别
0 引言
随着电子技术的发展和成熟,电子干扰在现代战争中日趋激烈,尤其是基于数字射频存储器(DRFM)的转发式欺骗干扰,日益成为雷达对抗的难点[1]。基于DRFM的转发式欺骗干扰能够精确模仿雷达的信号特征,使其获得与目标回波相同或近似的接收机增益,大量消耗雷达的资源并掩护真实目标。因此,欺骗干扰的识别与抑制是研究雷达抗干扰的一个重要方向。
国内外学者针对欺骗干扰的识别作了大量的研究。文献[2-3]根据DRFM相位量化位数引起的谐波效应对雷达欺骗干扰进行了识别,但量化位数大于4时,谐波效应减弱,方法失效。文献[4]利用联合点迹位置信息和速度信息,通过数据融合进行真假目标识别,但是需要对组网雷达的数据进行联合分析,所需时间较长。文献[5]针对高分辨率分时极化测量雷达,综合利用高分辨信息和极化信息的差异进行干扰识别,但是存在极化信息测量复杂的缺点。文献[6-7]利用盲分离技术对雷达欺骗干扰进行识别和抑制,其中文献[6]提出利用微多普勒特征盲分离的方法进行真假目标识别,具有一定的研究价值。
微多普勒效应是指由质心平动以外的振动、转动和加速运动等微小运动引起的目标回波信号的频率调制效应[8],主要用于目标精确识别。文献[9]利用延迟共轭相乘保留平动信息而消除微动的影响,从而实现对平动参数的估计问题,进而准确识别出目标特性。文献[10]利用海浪引起的舰船和角反射器摇摆频率的不同,提取微动特征差异,对角反射器和舰船目标进行了分类识别。
文献[11]指出机翼在飞行过程中会产生微小振动,特别是在目标进行非合作机动时(大攻角俯冲、大仰角攀升等),颤振现象会在一定的姿态角范围内对雷达的载波进行调制,产生含有周期性调制成分的雷达回波信号。而实际应用中自卫式干扰机或干扰吊舱由于位于机身中心或拖曳于机身之后,可以认为只具有与目标质心一致的平动或远小于机翼微动的微弱振动。基于这一现象,本文建立了目标回波和距离拖引欺骗干扰信号的微动模型,并利用MATLAB对回波信号进行仿真分析,提取二者之间的微动频率差异,从而完成对欺骗干扰的识别。
1 信号数学模型
为简化分析,以翼端为散射点建立模型,如图1所示,(U,V,W)为雷达坐标系,雷达静止位于坐标原点Q。(X,Y,Z)为参考坐标系,且与参考坐标系平行,其坐标原点O在雷达坐标系中的方位角和仰角分别为α和β。散射中心P在平动(平动速度为v)的同时作以点O为振动中心沿着某一定向轴的周期性振动,定向轴在参考坐标系中的方位角和俯仰角分别为α0和β0。两坐标系之间的位移矢量为R0,初始时刻P点在参考坐标系的位置矢量r0=(rX0,rY0,rZ0)T,经时间t后,目标中心O移动到O',参考坐标系作相应平移,P点运动到P'位置,在参考坐标系中对应的位置矢量r=(rX,rY,rZ)T。
由上述分析可知,雷达到散射点P'的位移标量和干扰机的位移标量分别可表示为:
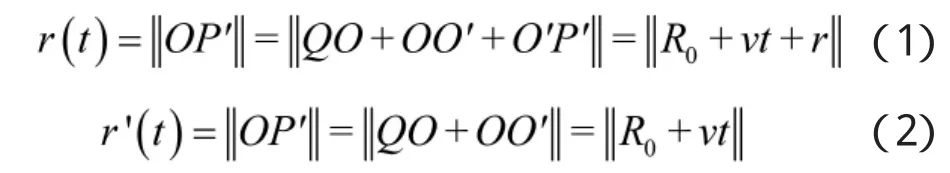
不失一般性,假设雷达发射的为正弦信号,则经过基带变换后的目标回波信号和干扰信号分别为:
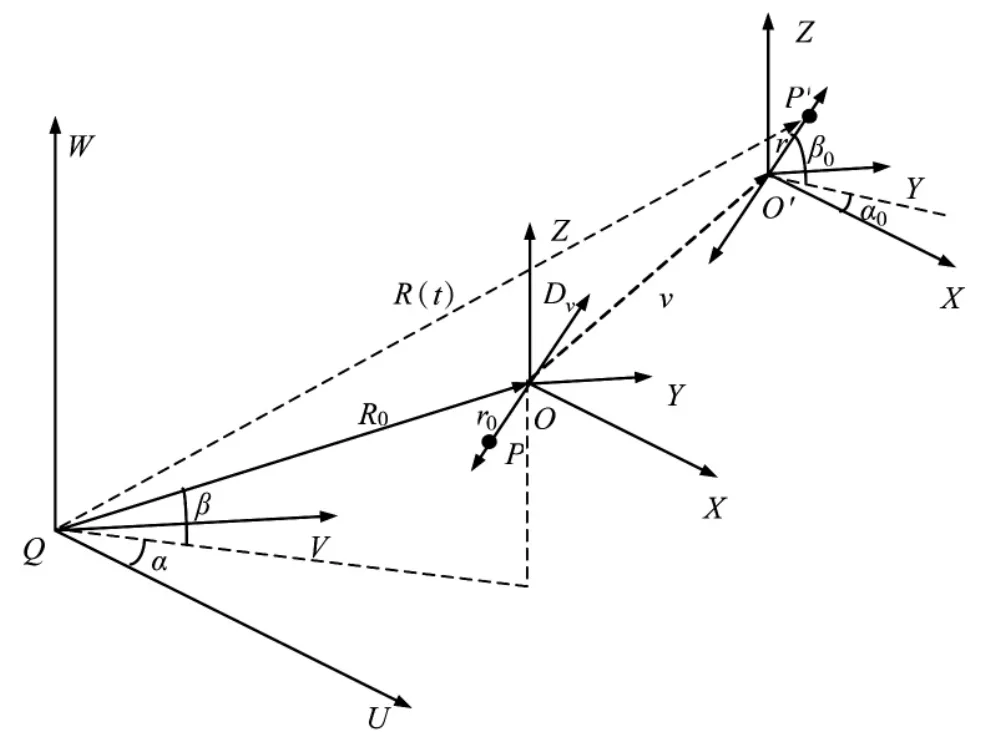
图1 振动散射点三维示意图
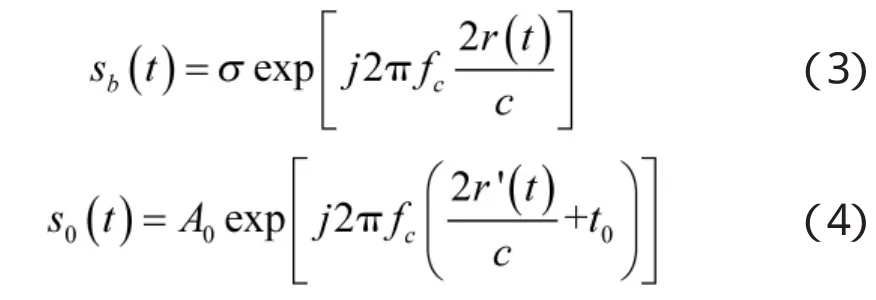
其中,σ为目标的反射率,c为电磁波的传播速度,A0为干扰信号的幅度,t0=at为距离拖引干扰时延函数。以目标回波为例,对相位求导,即可得到多普勒频率:
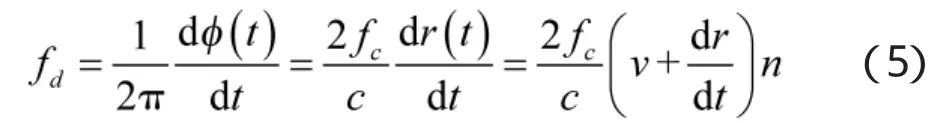
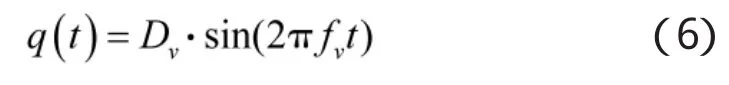
其中,q(t)是描述运动规律的时间函数,Dv是振动幅度,fv是振动频率。则P'到O'的距离变化为,即。分析式(5)可知,第1项为目标平动引起的多普勒频率,第2项为目标振动引起的微多普勒频率,对于目标回波信号而言:

同理,干扰信号经平动补偿后的多普勒频率为:
由式(7)和式(8)可知目标的微多普勒特征为周期函数,该周期等于目标的振动周期而与振幅以及雷达参数无关,而干扰信号只有拖引时延引起的固定多普勒频率,该频率只与拖引干扰的时延规律有关。因此,通过对fm-d进行谱分析可以得到接收信号的振动频率并进行目标识别。
2 信号特征提取与识别
2.1信号微多普勒仿真
由于飞机实际飞行时,机翼振动的幅度和频率都比较小,因此,在雷达分辨率较低、成像准确度较低的情况下,振动对回波调制影响不大。但是随着毫米波雷达的应用,由于其高分辨力、宽工作频带、大数值的多普勒频带响应、短波长易获得目标细节特征和清晰轮廓成像的特点[11],使其能够较为清楚地观察到翼端振动现象,因此,观测微多普勒特征需要较高的雷达频率。
对雷达接收信号进行微多普勒分析,设置仿真参数如下:参考坐标系原点到雷达的径向距离为10km,翼尖以O点为振动中心,作振幅为0.04 m的机械振动,振动角速度为ωv=8π rad/s,单频脉冲信号雷达载频fc=30GHz,脉冲重复频率为2 kHz,参考点为O,O在雷达坐标系中的方位角和仰角分别为0°和30°,翼尖在本地坐标系中的方位角和仰角分别为45°和0°,干扰机只作与质心一致的平动,距离拖引干扰时延为t0=1.6×10-8t。仿真中采用Gabor变换时频分析工具提取目标回波的时频图(TFD)信号。则利用文献[9]的平动补偿方法处理后得到的接收信号的微多普勒如图2所示。
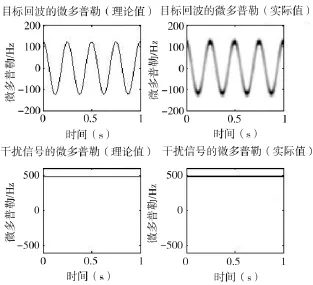
图2 雷达接收信号的理论值和实际值
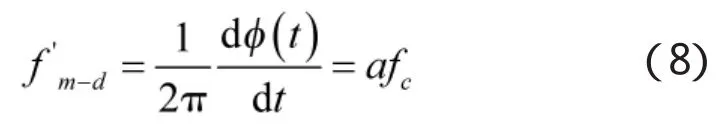
由图2可以看出经过平动补偿后接收信号的多普勒频率实际值与理论值相一致,目标回波信号的微多普勒为周期变化,且均值为零,而干扰信号的多普勒频率为恒定值,且均值远大于零,提取信号的微动频率和多普勒频率的均值能够反映目标回波和干扰信号的差异,用来识别欺骗干扰信号。
2.2欺骗干扰特征提取
文献[12]指出Viterbi算法能够在高噪声的环境下提取回波信号的微多普勒特征。Viterbi算法是一种寻找最可能隐状态的动态规划算法,该算法基于两个假设:①瞬时频率对应的时频点幅度尽可能大;②相邻时刻瞬时频率的变化范围较小。则瞬时频率的估计即为寻找TFD上代价函数之和最小的一条路径:

其中,p(k(n);n1,n2)为代价函数h(x)和g(x,y)沿着TFD上一条路径k(n)从时刻n1到时刻n2的代价之和。K是所有路径的集合,g(x,y)是的非增函数,h(x)为非减函数。因此,某一时刻某个时频点的值越大,该时频点就越有可能成为该时刻的瞬时频率点。在时刻n,将TF(t,f)排列成非增序列:
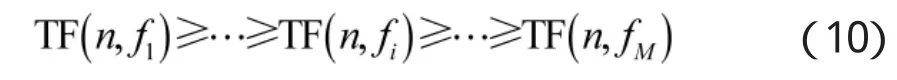
则函数h(x)和g(x,y)可以分别定义为:
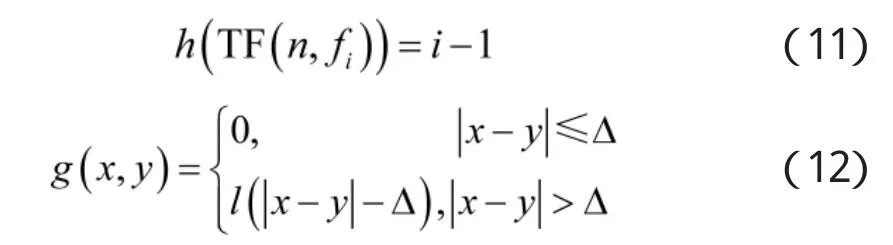
实际操作中,Δ取决于时频分布的频率分辨率,以上代价函数形式只是h(x)、g(x,y)的一种可能形式。对Viterbi算法提取的曲线依次进行Hilbert变换和FFT频谱分析即可得到信号的微动频率。设置干噪比JNR=0 dB,信噪比SNR=-6 dB,对雷达接收信号进行Viterbi提取,然后进行谱分析,结果如下页图3所示。
由图3可以看出利用Viterbi算法和谱分析能够在高噪声的环境中提取目标回波和干扰信号的微动频率和多普勒频率幅值的均值,为干扰信号的识别奠定了基础。
2.3欺骗干扰识别算法
根据所提取的特征参数多普勒频率均值可以构造特征因子α如下:
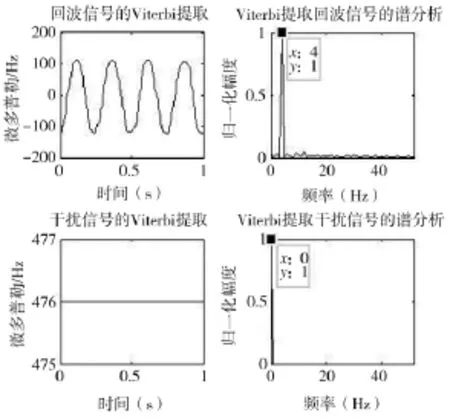
图3 Viterbi算法提取结果

根据所提取的特征参数微动频率可以构造特征因子β如下:

由于多普勒频率均值在数量上远大于微动频率,因此,构造联合特征因子γ如下:

根据联合特征因子的定义可以看出,由于干扰信号的均值远大于目标回波的均值,而目标微动周期为4,干扰微动周期为零,所以干扰信号的特征因子分布在1附近,而目标回波的特征因子分布在微动频率4的附近,从而γ能够区分目标回波和欺骗干扰。在信噪比SNR为-12dB、-6dB的情况下,分别做500次仿真实验,得到γ的分布如图4所示。

图4 联合特征因子γ的分布
由图4可以看出,在信噪比为-6 dB的情况下目标回波的联合特征因子分布在4的附近,干扰信号的联合特征因子分布在1附近,与理论分析一致。在信噪比为-12dB的情况下,目标回波的联合特征因子较为杂乱,且远离4,是因为Viterbi算法在这一信噪比下提取微多普勒特征失效;而干扰信号的联合特征因子始终保持在1附近,是因为特征因子的定义所致。
根据联合特征因子γ的分布和理论计算,设置阈值3.6和1.5对目标和干扰进行识别仿真。大于阈值3.6的为目标回波,而小于阈值1.5的为干扰信号。为消除信号幅度的影响,对雷达接收信号进行幅度归一化处理,即处理信号的干信比JSR=0 dB。信噪比变化范围为-12dB到0dB,每个信噪比下进行500次试验,得到识别概率曲线如图5所示。
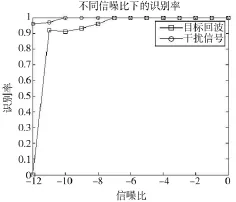
图5 不同信噪比下的识别率曲线
由图5可以看出干扰信号识别率高于目标回波信号的识别率,在信噪比为-12dB的情况下,目标回波识别率急剧下降为0。这一结果与前文理论分析一致,是由于特征因子的定义和Viterbi算法提取目标回波微动周期的失效所致。但在较高的信噪比下,目标回波和干扰信号的识别率均达到1,可见该方法能够有效地识别欺骗干扰和目标回波。
3 结论
本文针对距离欺骗干扰和目标回波信号在慢时域微多普勒频率的差异,建立了二者的数学模型,并在提取特征参数的基础上对欺骗干扰进行检测识别。仿真结果验证了算法的正确性。但本文算法所需的数据量较大,对信号观测的时间较长,下一步需要寻找能够缩短处理时间的特征提取方法。由于速度欺骗干扰与距离欺骗干扰在多普勒调制上具有一致性,因此,本文算法能够移植到速度欺骗干扰的识别中。
[1]AKHTAR J.Orthogonal block coded ECCM schemes against repeat radar jammers[J].IEEE Trans on Aerospace and ElectronicsSystems,2009,45(3):1218-1226.
[2]孙闽红,唐斌.雷达DRFM欺骗干扰的检测[J].信号处理,2010,26(5):672-676.
[3]卢云龙,李明,闫琰.利用调频率匹配的DRFM欺骗干扰检测方法[J].西安电子科技大学学报,2014,41(5):67-73.
[4]赵珊珊,张林让,周宇,等.组网雷达点迹融合抗假目标干扰方法[J].电子科技大学学报,2014,43(2):207-211.
[5]李永祯,王雪松,肖顺平,等.有源假目标的高分辨极化鉴别研究[J].兵工学报,2005,26(6):754-760.
[6]罗双才.基于盲分离的雷达有源欺骗干扰抑制方法研究[D].成都:电子科技大学,2012,5,55-60.
[7]尹洪伟,李国林,路翠华.基于盲分离的单通道LFM引信欺骗干扰抑制[J].电讯技术,2014,54(11):1475-1481.
[8]张群,罗迎,何劲.雷达目标微多普勒效应研究概述[J].空军工程大学学报(自然科学版),2011,12(2):22-26.
[9]贺思三,赵会宁,张永顺.基于延迟共轭相乘的弹道目标平动补偿[J].雷达学报,2012,3(5):505-510.
[10]黄孟俊,赵宏钟,付强,等.一种基于微多普勒特征的海面角反射器干扰鉴别方法[J].宇航学报,2012,33(10):1486-1491.
[11]徐艺萌,管桦,王国正,等.基于复数经验模式分解的空中颤振目标成像[J].光子学报,2014,43(6):21-29.
[12]关永胜,左群声,刘宏伟.高噪声环境下微动多目标分辨[J].电子与信息学报,2010,32(11):2630-2635.
[13]葛大江,周光彬,胥大川,等.GPS接收机的一种空时零陷抗欺骗式干扰方法[J].四川兵工学报,2015,36(8):41-45.
A Deception Jamming Identification Method Based on Micro-Doppler Feature
YANG Shao-qi,TIANBo,ZHAOShuang,HE Si-san
(School of Air and Missile Defense,Air Force Engineering University,Xi’an 710051,China)
In order to enhance the radar anti-jamming capability and promote the effectiveness of choosing anti-jamming measures,a novel jamming recognition method is proposed based on micro-Doppler feature.Firstly,the mathematical models of real target and jamming signal are established,and the differences of their micro-Doppler features are analyzed.Secondly,the instantaneous Doppler and micro-Doppler parameters of radar echo are extracted by the Viterbi algorithm and FFT spectral analysis.Finally,the feature factor which is less affected by the SNR is defined,according to which the target and the jamming are identified by the set threshold.Simulation results based on synthetic data show that the identification algorithm is correct and steady,which indicates the method is able to identify the deception jamming in a high noise environment.
micro-doppler,viterbi,featureextraction,jammingrecognition
TN971+.1
A
1002-0640(2016)10-0021-04
2015-08-23
2015-09-16
国家自然科学基金(61372166);航空科学基金资助项目(20130196001)
杨少奇(1992-),男,安徽阜阳人,硕士研究生。研究方向:新型电子对抗技术等。

