用于卫星干扰源定位的压缩感知DOA估计方法*
赵宏伟,刘波,刘恒
(西安空间无线电技术研究所,西安710100)
用于卫星干扰源定位的压缩感知DOA估计方法*
赵宏伟,刘波,刘恒
(西安空间无线电技术研究所,西安710100)
针对传统测向方法的实际应用性能较差,提出一种基于压缩感知(CS)的卫星干扰源定位方法。根据干扰信号方位角的空间稀疏性,建立了压缩感知波达方向(DOA)估计模型。通过协方差矩阵的高阶幂逼近信号子空间和矩阵的共轭对称特征,利用高阶幂矩阵的主对角线下左下角列向量进行波达方向估计。仿真实验验证,该方法不需要已知干扰源数,具有较高的精度和较好的分辨力,且能满足对相干干扰信号的估计。对压缩感知DOA估计在卫星干扰源定位中的应用具有一定参考意义。
卫星干扰源定位,波达方向估计,压缩感知,协方差矩阵,高阶幂
0 引言
通信卫星广泛采用的广播型通信方式使上下行链路易受干扰,从而通信质量发生恶化[1]。卫星轨道的日益拥挤、地球站数量的剧增,以及人为阻塞卫星通信,导致卫星受干扰事件屡见不鲜。如何精确定位干扰源是卫星通信领域必须要解决的关键问题。美国Milstar卫星可在检测到干扰源后,迅速将天线零点对准干扰源从而达到抑制干扰的目的。
卫星通信系统实现干扰源定位的传统技术途径主要有:到达时间差测向,需要两颗通信卫星相互配合实现[2];幅度比较式测向,灵敏度低;相位干涉仪测向,不具备同频信号或同信道信号的测向能力[3]。并且,这些技术都难以实现多个干扰源的精确定位。近年来,基于阵列信号处理的波达方向(DirectionofArrival,DOA)估计技术在卫星干扰源等多目标定位领域得到了广泛的关注[4-6]。然而,MUSIC等经典方法在高信噪比、足够大的快拍数以及非相干信号源的条件下,才可以很好地实现目标定位。
压缩感知(CompressedSensing,CS)理论是信息论和信号处理领域的一项新兴技术。基于阵列接收信号的空域稀疏性,可将CS理论应用到空域多目标测向中,其主要优势是天线阵元分布形式、接收信号的相干性都不影响测向性能,对快拍数要求比较低,并且能够较好地重构信号强度[7]。文献[8]提出了针对MIMO雷达的压缩感知DOA估计方法;文献[9]根据米波雷达的特点改进了压缩感知DOA估计算法的性能;文献[10]研究了其在声矢量阵中的应用。
查询国内外公开发表的文献,还未发现有文献将压缩感知DOA估计方法应用到卫星干扰源定位方面,并且目前文献多以一维直线阵列作为研究对象。鉴于此,在卫星干扰源定位的应用背景下,本文提出一种无需信源数的高分辨力CS DOA估计方法。在二维阵列CS DOA估计模型基础上,通过阵列协方差矩阵的高阶幂逼近信号子空间,利用高阶幂矩阵的共轭对称特征重构信号向量建立进行DOA估计。
1 基于二维阵列的CS DO A估计理论
假设K个窄带干扰信号入射到M个阵元的二维阵列,由于实际干扰目标仅占据少量的空间角度分辨单位,因此,干扰目标可以构成一个稀疏向量,构造N×L维的稀疏向量矩阵S(t)=[s1(t),s2(t),…,sN(t)]T,N(N>>K)为稀疏空间角度数量,L为快拍数量。稀疏向量矩阵S(t)的N个行向量中有K个非零向量,分别对应着实际的K个信号,其余N-K个行向量为零向量(或极小值,代表背景噪声值)。
在整个搜索空间的N个角度上进行扫描,使其包含所有可能的空间角度,扩展阵列流型矩阵构造M×N维的过完备原子库

式中,a(θi)为第i个信号的导向矢量,a(θi)=[exp(jω1),exp(jω2),…,exp(jωM)]T,ω表示信号频率,m=(dmxcosθ+dmysinθ)/c表示第m个阵元位置相对坐标原点的时延,(dmx,dmy)为第m个阵元的坐标,c为传播速度。
基于压缩感知理论的DOA估计模型为

式中,E(t)=[e1(t),e2(t),…,eM(t)]T为阵列测量噪声矢量,服从复高斯分布;假设通信功率比干扰功率低很多,将其近似为噪声;ε为正则化系数。
采用凸优化或贪婪类重构算法对S进行恢复重建,得到其估计值Sˆ,功率谱为

2 未知源数的CS DO A估计算法
传统MUSIC算法以及文献[11]中的基于奇异值分解(SVD)的CS DOA估计,都需要已知准确信源数,信源数估计错误时,性能下降严重。在卫星干扰源定位应用中,难以预知干扰源数目,符合实际应用环境的实时、稳健的源数判定方法还是目前有待解决的研究难点。因此,本文提出一种无需信源数的CS DOA估计方法。
2.1阵列协方差矩阵的高阶幂
对输入信号的相关矩阵R进行特征分解

式中,λi(i=1,…,K)为大特征值为白噪声功率,v1,v2,…,vK构成信号子空间US,vK+1,vK+2,…,vM构成噪声子空间UN,ΛS=diag{λ1,λ2,…,λK},ΛN=diag{λK+1,λK+2,…,λM}。实际应用中,数据相关矩阵R由快拍数据估计得到


实际验证,m取有限整数(如3~5)就能获得好的收敛效果。并且,为了降低幂运算的计算量,对R进行归一化处理。
2.2DOA估计模型
利用信号子空间与导向矢量的关系,式(7)改写为

G的第(p,q)个元素为

由于协方差矩阵的高阶幂Rm为共轭对称矩阵,其右上角三角形元素可由左下角三角形矩阵元素共轭表示,省略主对角线上的元素,对左下角三角形元素按列拼接形成一个新的向量

直接求解式(2)的L0范数问题是一个NP难题,为了方便求解,将其转化为L1范数问题。又考虑含有噪声,相应的CS DOA估计模型转化为最小化目标函数问题

式中,A=[b(θ1),b(θ2),…,b(θN)],b(θi)=[exp(jω(2-1)),…,exp(jω(M-1)),…,exp(jω(M-M-1))],η=[η1,η2,…,ηN]T;正则化参数ε与噪声功率有关。
2.3算法步骤
基于压缩感知的干扰信号DOA估计算法步骤总结为:
①利用接收信号数据构建协方差矩阵R,计算式(7)中高阶幂Rm;
②矩阵Rm为共轭对称结构,取其主对角线左下角三角形元素按列重排,形成式(10)中的向量g;
③对搜索空间进行等间隔取角(通常为0.1° ~1°),得到N个角度,构造过完备原子库A,如式(11);
④利用二阶锥规划法[11]求解CS DOA模型(11),对向量η进行恢复重构;
⑤根据重构向量η中的功率谱峰值获得对应的DOA目标角度值。
3 仿真实验与分析
本节通过理想阵列流型(不考虑通道不一致性和互耦等的影响)和实测方向图数据,对基于压缩感知理论的卫星干扰源DOA估计进行仿真研究分析。仿真中接收阵为7个阵元组成的六边形阵,阵元间距为半波长。假设干扰目标为窄带随机信号,信号形式不限,信号幅度服从零均值,方差为1的复高斯变量;假设通信功率远小于干扰功率,将其近似为噪声;加性复高斯噪声与干扰信号互不相关。
实验1低干噪比下的算法性能对比。假设两个独立干扰信号来自20°和30°,干噪比为0 dB,快拍数为200。比较本文子空间算法、文献[12]基于协方差矩阵算法和MUSIC算法(假设信源数已知)如图1所示。在低干噪比和有限快拍数下,MUSIC算法无法正确划分信号和噪声子空间,导致算法失效。文献[12]直接通过协方差矩阵构建信号向量,在低干噪比条件下难以去除噪声对算法的影响,估计结果容易出现伪峰。本文算法通过协方差矩阵的高阶幂提取信号子空间构建信号向量,提高算法的抗噪性,能够提供高精度的DOA估计结果。
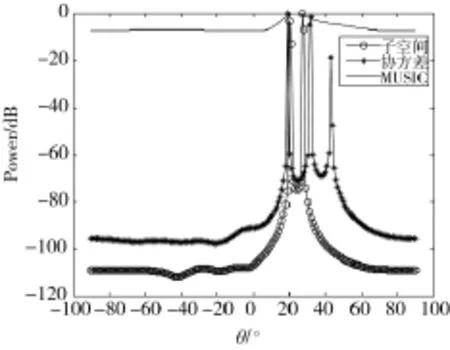
图1 低干噪比下算法性能对比
实验2算法的分辨力对比。假设两个独立干扰信号来自20°和25°,干噪比为10 dB,快拍数为200。比较本文子空间算法、文献[13]基于协方差矩阵特征向量算法和MUSIC算法(假设信源数已知)如图2所示。由于只有7个阵元可以利用且干扰信号方位间隔非常小,MUSIC算法谱峰非常模糊,难以准确分辨某一个干扰源。基于特征向量算法谱峰非常尖锐,但只能分辨一个干扰源。本文算法通过式(10)重构信号向量,增加信号向量的维数相当于将阵元数M虚拟加倍至M(M-1)/2,大大提高了算法的分辨能力,谱峰非常尖锐,能够准确分辨两个干扰源。

图2 算法分辨力对比
实验3基于实测方向图数据的相干源定位分析。考虑DOA估计算法在卫星干扰源定位应用中的两个主要问题:①系统误差的存在,如接收通道失配、阵元位置误差等,导致无法用理想阵列流型进行测向,也很难用固定函数描述方向矢量。这需要采用天线阵元的远场波束方向图代替理想阵列流型。②相干源的普遍存在,如信号传输过程中的多径现象,或者敌方有意设置的电磁干扰。
假设两个相干干扰信号来自30°和40°,干噪比分别为10dB和0dB,快拍数为200。如下页图3所示,传统MUSIC算法无法获得准确估计,而空间平滑MUSIC算法会降低算法分辨力。基于压缩感知DOA估计算法对信号相关性不敏感,无需特殊处理。除此之外,相对于MUSIC算法中谱峰的大小只用于谱峰搜索,没有物理含义,而压缩感知理论的本质是重构来波的功率强度,因此,在得到方位角度的同时,能够比较准确地重构信号强度,对抗干扰时有助于形成不同深度的零陷方向图。

图3 基于实测方向图数据的相干源估计
4 结论
本文研究了基于压缩感知理论的卫星干扰目标DOA估计方法,该方法不需要已知干扰源数目,增强了算法的鲁棒性;具有很高的估计精度和分辨率,能够适用于低信噪比和相干源等应用场合。仿真实验分别通过理想阵列流型和实测方向图数据验证算法的可行性和有效性。该方法还可扩展到二维DOA参数(方位角和仰角)的提取,对卫星干扰源定位应用具有较高的参考价值。
[1]徐烽,陈鹏.国外卫星移动通信新进展与发展趋势[J].电讯技术,2011,51(6):156-161.
[2]郝才勇,刘恒,刘宏立.基于TDOA的卫星干扰源定位方法的研究[J].重庆邮电大学学报,2012,24(4):442-446.
[3]陆安南,缪善林.星载测向定位技术研究[J].航天电子对抗,2014,30(1):13-16.
[4]JAMES H G.High-frequency direction finding in space[J]. ReviewofScientificInstruments,2003,74(7):3478-3486.
[5]程安启,王华力.基于卫星平面阵列多波束天线波束空间的自适应调零和干扰源定位技术[J].电子学报,2008,36(7):1279-1283.
[6]孙海浪,陶海红,张娟.用于星载赋形天线的基于频域多相干目标测向算法[J].宇航学报,2010,31(3):830-837.
[7]黄传禄,晁坤,毛云志.基于压缩感知的空间谱估计[J].电波科学学报,2014,29(2):150-157.
[8]MARCO R,ALEXANDER M,YONINA C.Spatial compressive sensing for MIMO radar[J].IEEE Transactions on Siganl Processing,2014,62(2):419-430.
[9]王园园,刘峥,曹运合.基于压缩感知的米波雷达低空测角算法[J].系统工程与电子技术,2014,36(4):667-671.
[10]付金山,李秀坤.声矢量阵DOA估计的稀疏分解理论研究[J].哈尔滨工程大学学报,2013,34(3):281-286.
[11]MALIOUTOV D,GETIN M,WILLSKY S A.A sparse signal reconstructionperspectiveforsourcelocalizationwith sensor arrays[J].IEEE Transaction on Signal Processing,2005,53(8):3010-3022.
[12]LIU Z,HUANG Z,ZHOU Y.Array signal processing via sparsity-inducing representation of the array covariance matrix[J].IEEE Transaction on Aerospace and Electronic systems,2013,49(3):1710-1724.
[13]李鹏飞,钟子发.未知信源数目的DOA估计方法[J].电子与信息学报,2012,34(3):576-581.
Satellite Interference Localization Method Based on the Compressed Sensing DOA Estimation
ZHAOHong-wei,LIU Bo,LIU Heng
(Xi’an Institute of Space Radio Technology,Xi’an 710100,China)
The conventional direction finding methods have poor performance in the actual application.A satellite interference localization method based on the compressed sensing theory(CS)is proposed.Based on the interference signal angle’s sparseness in angle space,the corresponding direction of arrival(DOA)model is constructed.This method approximates the signal subspace through the high-order power of the spatial covariance matrix.Then the column vector in the lower left corner of the main diagonal of the high order power matrix is extracted to do DOA estimation.The experimental results show the method is better than the MUSIC algorithm in the aspects of resolution,accuracy,and capability of estimating coherent signals without the number of signals.This promotes the application of compressed sensing in satellite interference localization.
satellite interference localization,direction of arrival estimation,compressed sensing,covariancematrix,highorderpower
TN975
A
1002-0640(2016)10-0025-04
2015-08-13
2015-09-16
国家自然科学基金资助项目(61201089)
赵宏伟(1982-),男,山东潍坊人,博士研究生。研究方向:空间谱估计技术。

