基于STAP杂波抑制的子阵优化技术

于　永，雷志勇

(南京电子技术研究所,　南京 210039)



·信号处理·

基于STAP杂波抑制的子阵优化技术

于永，雷志勇

(南京电子技术研究所,南京 210039)

新一代相控阵雷达的天线阵列规模庞大，一般含有几百乃至上万个阵元。在阵元级实现自适应波束形成抗干扰和空时自适应处理杂波抑制，会极大地增加系统开销，甚至难以实现。在实际应用中，考虑到系统成本、信号处理运算量等因素，需要将大型阵列划分为适当的子阵，以减小接收所需通道数。文中通过子阵优化划分数学建模，研究子阵划分对干扰、杂波抑制性能的影响，探索最优子阵划分的数学求解方法，为大型阵列雷达研制提供理论支撑和工程可实现算法。

自适应数字波束形成；空时自适应处理；子阵划分； 最优化方法

0　引　言

为满足信噪比、波束宽度等指标，相控阵天线一般由包含几百乃至上千个阵元的大型阵列组成。在阵元级实现自适应波束形成(ADBF)抗干扰和空时自适应处理(STAP)杂波抑制，会极大地增加系统开销，甚至难以实现。实际应用中，考虑系统成本、信号处理运算量等因素，往往将大型阵列划分为适当的子阵，以减小接收通道数。不同子阵划分方式会对信号处理中的ADBF、STAP处理产生影响，最终影响雷达检测性能。子阵优化划分问题，即按照特定的优化准则将整个天线阵面划分为若干子阵，从而在子阵级进行自适应处理以减小运算复杂度和系统成本，同时使得降维处理与全阵处理相比性能损失最小。

关于子阵优化问题，文献[1]研究了两种非均匀子阵结构，提出构成子阵的相邻子阵中心间距无公约数原则。文献[2]基于子阵级和差波束方向图性能提出了基于锥削函数的子阵优化方法。此后，文献[3]分析了等规模交叠子阵划分对STAP的影响，文献[4]将多目标遗传算法用于子阵优化划分，文献[5]利用混合染色体遗传算法对子阵和差波束进行了优化。文献[6-7]提出了等噪声功率法及等子阵加权法的子阵划分准则，并研究了子阵划分对STAP的影响。文献[8]等将遗传算法用于最优子阵划分问题并取得了一些进展。文献[9-12]等也对子阵优化划分的相关研究工作进行了总结。

从这些文献中，概括出的主要划分准则包括：

(1)从阵面方向图角度，应尽量减小栅瓣效应对子阵级杂波抑制的影响，如使副瓣电平最小化；

(2)从自适应处理角度，应尽量减少杂波自由度，同时保证子阵级系统自由度满足杂波抑制要求。

具体的指导性准则有：子阵间的间距无公约数；不同子阵的阵元数目不完全相同，子阵的规模尽量接近；子阵的结构关于阵列中心对称；均匀不交叠、均匀交叠和非均匀划分等。

本文重点考虑子阵优化划分的数学建模问题，根据不同工程应用的实际需求建立不同的优化目标函数及最优化数学模型。在最小化信杂噪比损失原则下，将改进的遗传算法应用于基于STAP杂波抑制的最优子阵划分问题中，给出了最优的天线阵面划分方式。

最后，利用实测数据分析验证了算法的有效性。

1　子阵优化划分建模

子阵划分问题模型建立如下：已知关于M、λ、d的函数F(θ)，

F(θ)=WMA，其中

(1)

WM=[w1, …, wk, …, wM]1*M,

(2)

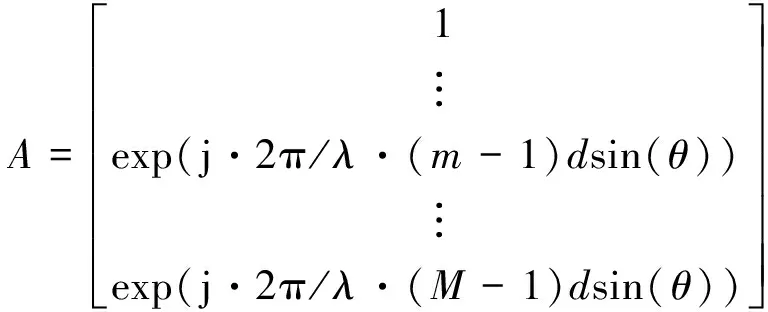
(3)

构建新函数FT(θ)

FT(θ)=ULTA

(4)

式中：d表示阵元间距；UL=[u1,…,ul,…,uL]1*L，

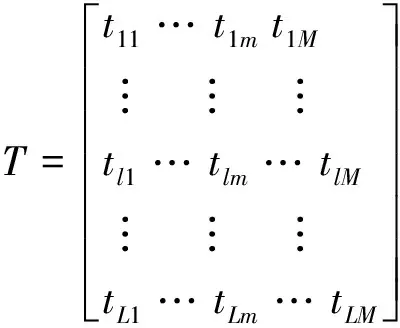
tlm∈{0,1},l=1,2,…,L；m=1,2,…, M

(5)

子阵划分优化即在阵元数和子阵数指定的前提下，将包含有M个天线阵元的大型相控阵划分为L个子阵,在子阵级进行自适应干扰/杂波抑制处理。不同的优化准则将导致不同的最优子阵划分方案。

(1)无干扰条件下方向图最优逼近准则

设F(θ)为理想的和波束方向图，在传统框架下，最优的子阵划分目标函数是

(6)

以最高副瓣电平作目标函数，则优化问题目标函数为

(7)

(2)干扰/杂波抑制性能最优准则

ADBF求最优权一般采用LCMV(线性约束最小方差)准则或者MMSE(最小均方误差)准则，其求解表达式为下述约束最优化问题

(8)

求得最优权为

(9)

对应输出SINR为

(10)

式中：Ps为期望信号功率；Ri+n为干扰与噪声的协方差矩阵。

子阵级ADBF的数学表达式为

(11)

其中，S=Ss，Ss=U⊙a(θ0)，a(θ0)=[1,exp(j·2π/λ·dsin(θ),…,exp(j·2π/λ·(M-1)dsin(θ))]T，⊙表示Hadamard乘积，aT(θ0)=Ta(θ0)，RT,i+n=THRi+nT。

杂波场景下通常采用空时自适应处理(STAP)实现杂波抑制，其原理与上述表达基本一致，只是导向矢量为空时两维形式，即S=Ss⊗St，其中

St=[1,exp(j·2πfd/fr), …,

exp(j·2πfd/fr·(K-1))]T

(12)

为时域导向矢量，⊗表示Kronecker积。

对应输出SINR为

(13)

式中：Ps为期望信号功率；RT，i+n为降维后的干扰与噪声的协方差矩阵。

此约束条件下对应的最优准则

(14)

2　基于遗传算法的子阵级STAP最优子阵划分

2.1约束准则数学建模

过于随意的划分不仅工程上不易实现，而且难以总结划分准则。结合实际工程能力，对子阵划分规则作如下限制：

(1)每个子阵包含阵元数量有一定限制；

(2)子阵间有限度交叠，即某个子阵不能完全包含另一个子阵；

(3)子阵内部阵元相互邻接；

(4)任何阵元必属于至少一个子阵。

按照设定的划分约束准则，其数学表达建模如下：

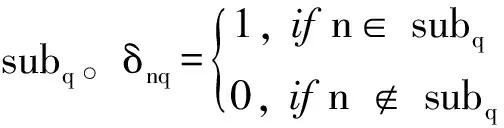
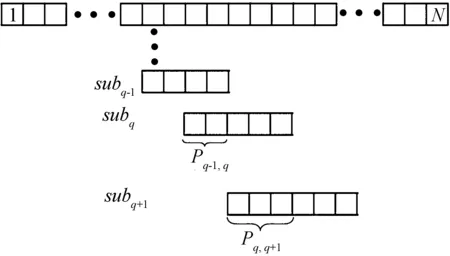
图1　子阵功分约束准则示意图

记子阵包含阵元数的最小值和最大值分别为Nmin和Nmax，子阵间交叠阵元数最小值和最大值分别为Pmin和Pmax，则划分T满足以下约束条件

(15)

通过Nmin和Nmax可调节子阵规模，Pmin和Pmax可调节子阵交叠程度，如Pmin=Pmax=0对应子阵间无交叠的情况。

2.2基于遗传算法的最优子阵化分算法设计

遗传算法其基本思想基于达尔文进化论和孟德尔的遗传学说，是一种基于自然选择和遗传变异等生物进化机制的全局性概率搜索算法。主要包括编解码方案设计，适应值函数设计，遗传操作设计等几个方面。

(1)编解码方案设计

采用十进制编码，编码长度为N+Q-1位。前N位表示子阵q(q=1,2,…,Q-1)中不与子阵q+1交叠的部分，后Q-1位表示子阵q与子阵q+1交叠程度，即交叠部分的阵元数。解码时先将前N位按照所属子阵进行解码，然后在每个子阵起始处按照交叠程度与前一个子阵进行交叠。

(2)适应值函数设计

好的编码结构具有较高的适应值，即具有较强的生存能力。由于适应值是种群中个体生存机会选择的唯一确定性指标，所以适应值函数设计至关重要，直接影响到遗传算法的收敛速度以及能否找到最优解。通常适应值函数由需要解决问题的目标函数本身或者变换得到。

(3)选择操作设计

选择策略采用线性排序结合精英选择，即生成下一代种群时，先复制当前种群中适应度较高的部分个体(如10%)，其余部分个体使用线性排序选择策略从当前种群中选取。

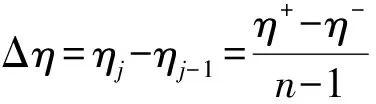
(16)

线性排序选择概率为

(17)

(4)交叉操作设计

交叉操作采用单子阵交叉，在进行交叉操作时，根据交叉概率从当前种群中选择一定数量的个体，然后对其两两配对进行交叉操作。步骤如下：

1)确定哪些子阵可交叉。找出两个体前N位中相同部分对应的子阵，只有对这些子阵进行交叉操作才不会破坏子阵的邻接性。

2)依次判断交叉操作后新个体是否满足划分要求。

3)在判定后的子阵中随机选取一个进行交叉操作。

(5)变异操作设计

根据变异概率计算个体发生变异的概率，并依据该概率从种群中选取一定数量的个体进行变异操作。考虑到子阵邻接性，选择子阵q的末尾位置进行变异操作，设子阵的变异概率为pm，则种群中个体发生变异的概率为

pm(xj)=1-(1-pm)Q, j=1,2,…,n

(18)

依此概率从当前种群中选取一定数量的个体，然后进行变异操作。

2.3仿真结果

按照2.2节设计的遗传算法，将8×40的天线阵面划分为20个子阵，优化目标为最大化样本数据中目标SNR，简记为最大样本SNR准则，其适配值函数

fitness=M+w×ΣSNRx-SNR0，

(19)

式中：M为固定常量，SNRx为某一划分方式下的目标信噪比，SNR0为参考目标信噪比，根据实际需要设置不同的权值w1和w2可调整优化目标。

初始阵面划分及优化后的阵面划分结构如图2所示。

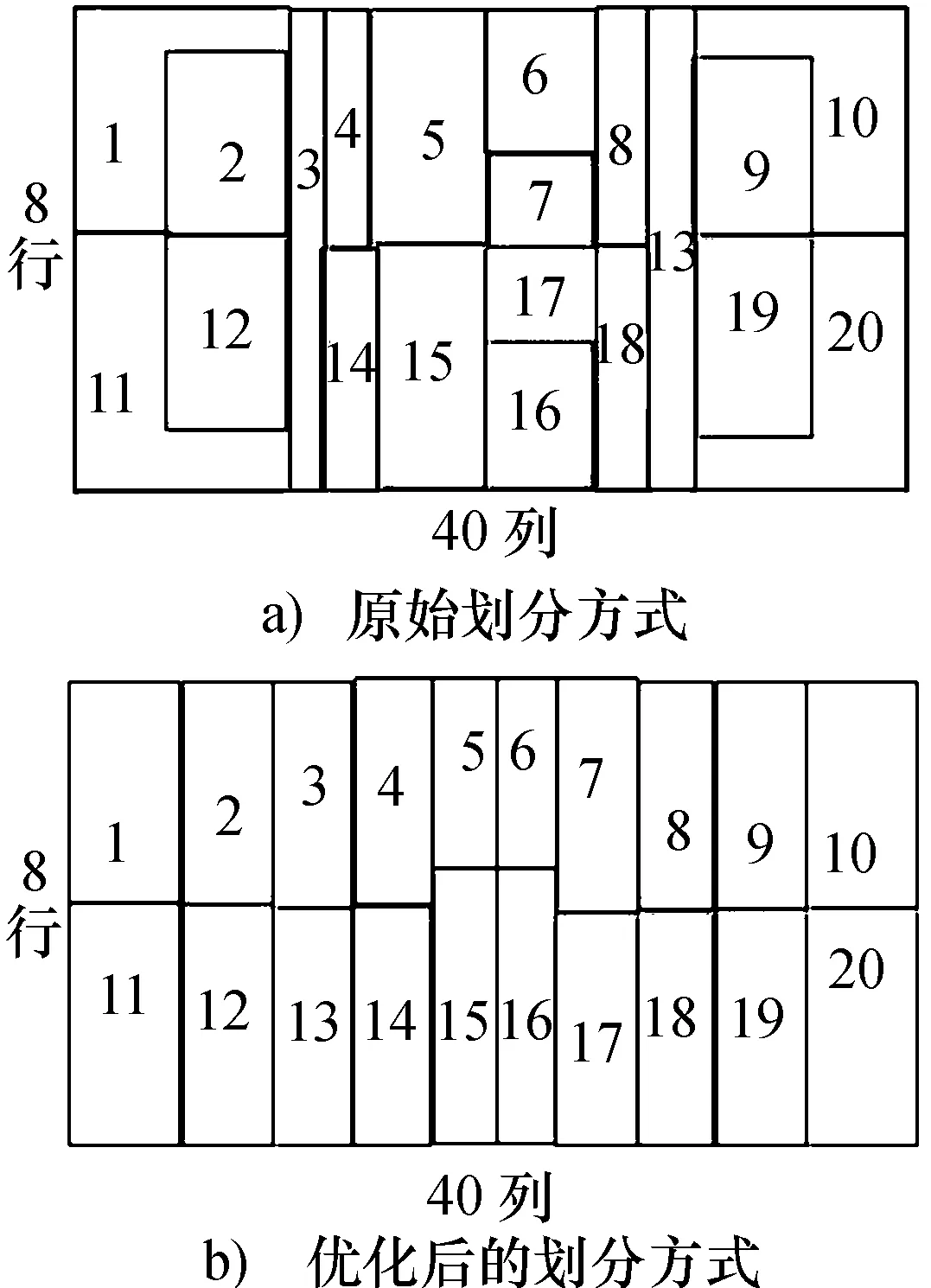
图2　20子阵原始划分与优化后划分形式

3　实测数据验证

试验共选用18组杂波回波数据，分别做原始阵面划分和优化子阵划分后的20个子阵STAP处理，统计副瓣杂波抑制剩余情况，统计时副瓣杂噪比按照相应PD处理的杂噪比做归一化。

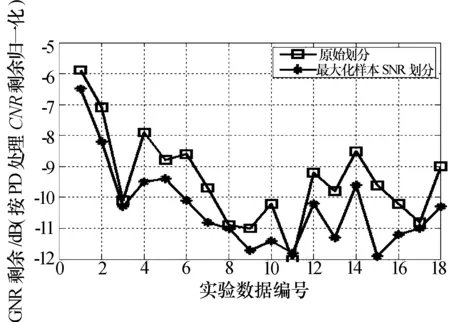
图3　18组数据不同子阵划分方式归一化副瓣CNR比较

18组数据中有14组子阵优化后比原始阵面划分的STAP副瓣杂波抑制改善大于0.5 dB，比例高达78%。其中，最大改善达2dB以上，平均性能改善 1 dB。子阵优化划分处理后子阵级STAP的杂波抑制性能得到明显提升。

4　结束语

本文研究了子阵优化划分的数学建模问题，给出了无干扰条件下方向图最优逼近准则、干扰/杂波抑制性能最优准则条件下的最优化问题数学模型。根据数学模型设计了子阵优化算法，并通过数据仿真验证了子阵优化算法的有效性。在实际工程应用中，存在着阵元位置误差、通道幅相误差、带内起伏等误差因素，算法在误差条件下的稳健性有待进一步验证。

[1]NICKEL U. Subarray configurations for interference suppression with array radar[C]// IEEE International Radar Conference.[S.l.]: IEEE Press, 1989: 82-86.

[2]NICKEL U. Subarray configurations for digital beamforming with low sidelobes and adaptive interference suppression[C]// IEEE International Radar Conference. [S.l.]: IEEE Press, 1995: 620-623.

[3]GAFFNEY J B, GUTTRICH G, BAHU B N S, et al. Performance comparison of fast-scan GMTI/STAP architectures[C]// IEEE International Radar Conference. [S.l.]: IEEE Press, 2001: 252-257.

[4]ANSELL D W, HUGHES E J. Using multi-objective genetic algorithms to optimize the subarray partitions of conformal array antennas[C]// IEEE International Conference on Antennas and Propagation. [S.l.]: IEEE Press, 2003: 151-155.

[5]MASSA A, PASTORINO M, RANDAZZO A. Optimization of the directivity of a monopulse antenna with a subarray weighting by a hybrid differential evolution method[J]. IEEE Antennas and Wireless Propagation Letters, 2006(5): 155-158.

[6]许志勇, 保铮, 廖桂生. 一种非均匀邻接子阵结构及其部分自适应处理性能分析[J]. 电子学报, 1997, 25(9): 20-24.

XU Zhiyong, BAO Zheng, LIAO Guisheng. A non-uniform contiguous subarray configuration and its performance of partially adaptive processing[J]. Acta Electronica Sinica, 1997, 25(9): 20-24.

[7]XU Z Y, BAO Z, LIAO G S. A method of designing irregular subarray architectures for partially adaptive processing[C]// CIE International Conference on Radar. [S.l.]: IEEE Press, 1996: 461-464.

[8]HU H, QIN W C. Research on subarray partitioning of planar phased array with adaptive digital beamforming[C]// IEEE 2007 International Symposium on Microwave, Antenna, Propagation, and EMC Technologies for Wireless Communications. [S.l.]: IEEE Press, 2007: 691-694.[9]张增辉, 胡卫东, 郁文贤. 遗传二进制多粒子群优化算法及其在子阵级STAP中的应用[J]. 信号处理, 2009, 25(1): 52-57.

ZHANG Zenghui, HU Weidong, YU Wenxian. Genetic binary multiple particle swarm optimization algorithm and application in subarrary STAP[J]. Signal Processing, 2009, 25(1): 52-57.

[10]熊子源, 徐振海, 张亮, 等. 基于聚类算法的最优子阵划分方法研究[J]. 电子学报, 2011, 39(11): 2615-2621.

XIONG Ziyuan, XU Zhenhai, ZHANG Liang, et al. Research on the optirmal subarry partition based on clustering algorithm[J]. Acta Electronica Sinica, 2011, 39(11): 2615-2621.

[11]VON A W H. Properties of phased arrays[J]. Proceedings of the IRE, 1960, 48(10): 1715-1727.

[12]ZHANG Q, MIKHAEL W. B., Estimation of the clutter rank in the case of subarraying for space-time adaptive processing[J]. IEEE Electronic Letters, 1997, 33(5): 419-420.

于永男，1985年生，博士，工程师。研究方向为雷达信号处理。

雷志勇男，1975年生，高级工程师。研究方向为雷达信号处理。

Optimization Technology of Subarray Division Based on STAP Clutter Suppression

YU Yong，LEI Zhiyong

(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

The antenna of phased array radar for the new generation is huge, and generally contains hundreds or even thousands of elements. Anti-interference by ADBF(Adaptive Digital Beam Forming) or clutter suppression by STAP(Space and Time Adaptive Performing) on the element level, could significantly increase the system load, and even hard to achieve. Considering the system cost and computation load of signal processing in practical, large array needs to be divided into proper subarrays, to reduce the required receiving channels. In this article, mathematical modeling of optimal subarray division, and also the influence to the performance of interference or clutter suppression are considered. In addition, the mathematical solution of optimal subarray division is also researched, which could provide theoretical and engineering algorithm to be realized on large scale array radar equipment.

adaptive digital beam-forming (ADBF)；space and time adaptive performing (STAP)；subarray division；optimization

10.16592/ j.cnki.1004-7859.2016.09.006

于永Email：yuyong6834@163.com

2016-04-20

2016-06-22

TP971.1

A

1004-7859(2016)09-0028-04