基于序列二次规划的粒子滤波算法

李　凡，毕红葵，段　敏，喻晨龙，丰　骁

(空军预警学院 a. 研究生管理大队；　b. 陆基预警监视装备系，　武汉 430019)



·数据处理·

基于序列二次规划的粒子滤波算法

李凡a，毕红葵b，段敏b，喻晨龙a，丰骁a

(空军预警学院 a. 研究生管理大队；b. 陆基预警监视装备系，武汉 430019)

针对传统粒子滤波(PF)没有引入当前信息，并存在粒子退化的问题，提出了一种基于序列二次规划(SQP)多级优化的PF算法。首先，基于残差分布特性采用置信区间剔除较大偏差粒子，调整粒子权值分布；然后，将重采样后的粒子映射到集合U，根据集合U中各粒子复制次数建立多级优化模型，通过SQP求解模型的参数值，当前后两级模型优化参数差异小于门限时，输出最后一级优化参数为滤波结果；最后，为防止过度采样导致粒子退化，利用滤波值及其协方差采样新粒子。仿真实验表明：SQP-PF算法在跟踪精度，粒子多样性方面优于传统PF算法。

粒子滤波；序列二次规划；多级优化；置信区间

0　引　言

粒子滤波(PF)算法是一种基于Monte-Carlo仿真的最优回归贝叶斯滤波算法，广泛用于机动目标以及多目标跟踪领域[1-5]，理论上适用任何噪声环境下的线性以及非线性目标跟踪问题[6]。但其概率密度没有引入当前信息导致大多粒子偏差较大，并且粒子退化问题严重。文献[7-12]通过扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)将最新观测信息引入PF的分布函数中，提出扩展卡尔曼粒子滤波、无迹粒子滤波算法，其后验概率分布更贴近真实分布，提高了跟踪精度，但对粒子退化问题改善不大。同时，由于EKF、UKF算法本身的局限性，在目标机动突变时容易出现误差尖峰。文献[13]提出一种基于有效粒子数门限判决的方法进行不完全重采样，解决了粒子退化问题，降低算法的运算负荷，但粒子耗尽问题严重。文献[14]提出一种加入混沌序列扰动粒子群优化的粒子滤波算法，混沌序列遍历性、随机性特点避免粒子群陷入局部最优，改善初始粒子质量，但低维混沌序列参数简单且对初值极为敏感。文献[15]提出一种重采样过程中基于被复制粒子与被抛弃粒子的线性组合产生新的粒子，增加粒子多样性，但算法的步长系数难以确定，且与经过线性组合的粒子相关。文献[16]提出一种分类权值局部重采样的PF，通过保留中权值粒子，大、小权值粒子组合产生新粒子抑制粒子过度采样，但权值分类较为困难。文献[17]提出使用模拟退火法通过递推更新系统模型的方式，实现重要性密度函数的在线更新，提高算法精度，但其收敛速度慢且对先验参数设置敏感。

本文针对PF算法没有引入最新观测信息并存在粒子退化的问题，提出一种基于序列次规划(SQP)多级优化的SQP-PF算法。传统PF算法粒子相异性较差，重采样导致大量小权值粒子被删除而大权值粒子多次复制，SQP-PF算法基于粒子残差统计特性分析，根据置信水平1-α选取置信区间内粒子，减小粒子权值分布跨度，并保证重采样的粒子基数；在重采样过程中，引用数学集合的概念，将重采样后粒子映射到集合U，利用U中粒子复制次数建立约束条件更新的多级优化模型，通过SQP求解引入最新观测信息模型参数，将PF滤波转化为非线性的SQP多级优化求解问题，当前后两级优化的结果差异小于门限时，输出最后一级优化参数为滤波结果；同时，利用滤波值及其协方差随机采样新粒子并入U中作为下一时刻初始粒子，改善粒子质量，保证粒子多样性，防止粒子过度采样导致跟踪失败。

1　SQP-PF算法

PF算法核心思想是用一组离散带权值的粒子表示目标状态，通过粒子预测、权值计算，经过重采样粒子的加权和作为最终的滤波输出。设系统空间状态模型为

X(k)=f(X(k-1), n(k-1))+Γ(k)n(k)

(1)

Z(k)=h(X(k),w(k))

(2)

式中：X(k)、Z(k)分别为k时刻目标状态向量与观测向量；f(·)、h(·)分别为系统状态方程与量测方程；Γ(k)为已知控制矩阵；n(k)、w(k)分别为独立的过程噪声向量、观测噪声向量。

1.1粒子筛选与重采样

在传统PF算法中，没有引入当前观测信息，其重要密度函数(IDF)所取粒子样本与实际后验分布样本偏差较大，IDF得到的大部分粒子对概率密度函数的贡献几乎为零，重采样后大权值粒子大量复制，导致下一时刻粒子相异性减弱，粒子的费效比很低[18-19]。本文基于综合残差分布特性，结合置信水平1-α确定置信区间，筛选区间内样本粒子。假定第i个粒子的预测残差为

Γ(k)n(k))]

(3)

(4)

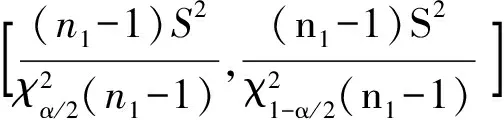
1.2基于粒子复制次数的多级优化模型

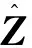
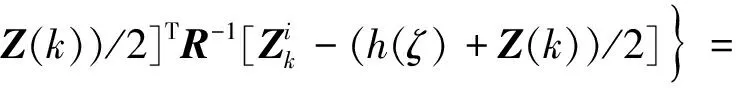
(5)

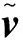
(6)

(7)

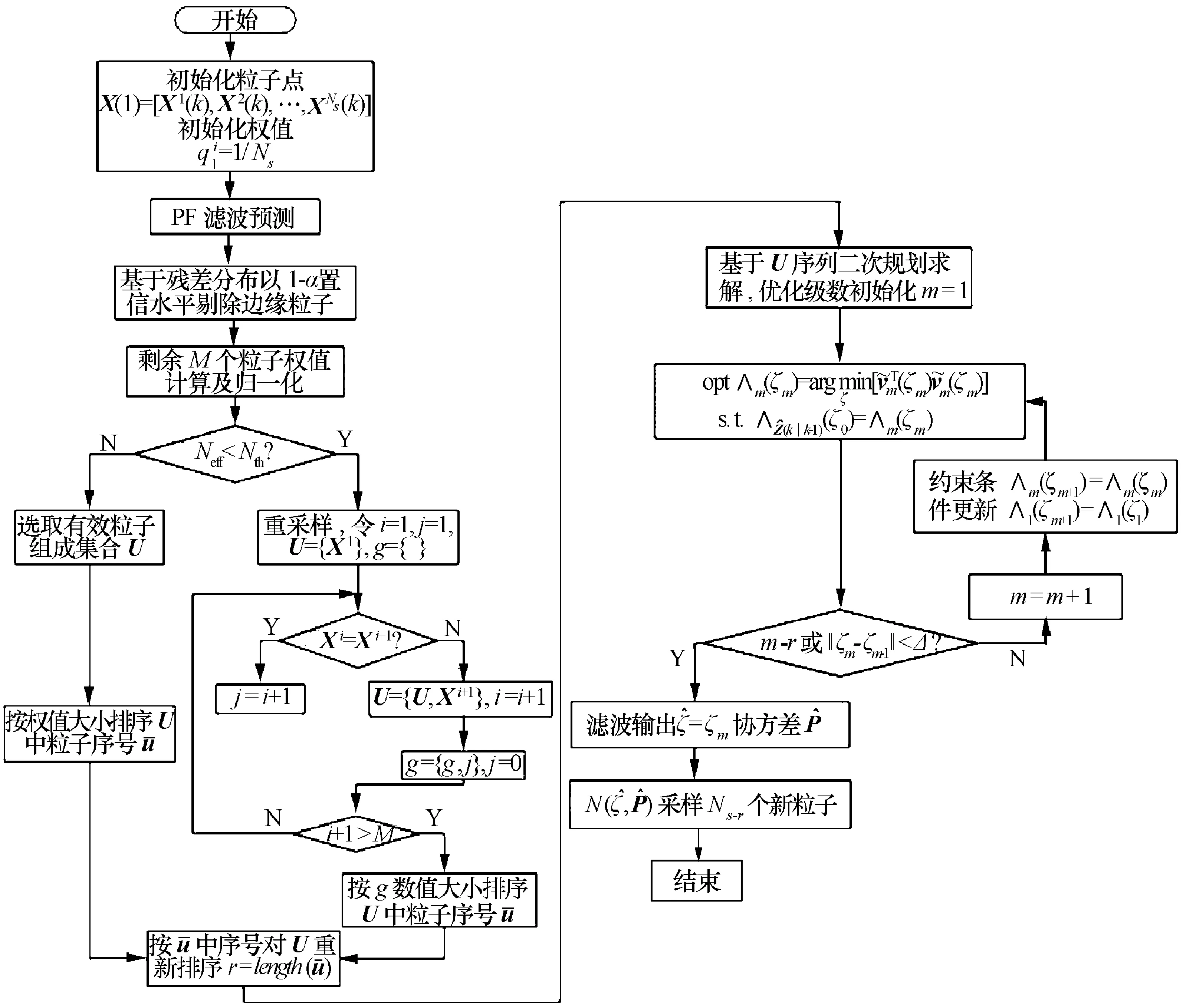
图1　SQP-PF算法流程图

算法具体步骤如下：

步骤1样本粒子及粒子权值初始化。

2　仿真分析

假定目标在15 km高空释放，巡航段有动力跳跃三次，无动力跳跃两次，最大飞行速度15.52 Ma，最大转弯速度3.14 rad/s，最大飞行高度96.93 km，全弹道射程988.97 km，飞行时间450 s。全弹道真实运动模式复杂，机动能力较强。为便于说明，选择标准粒子滤波(SIR)、辅助粒子滤波(APF)[22]以及SQP-PF算法进行对比，设状态转移矩阵为

(8)

控制矩阵为

(9)

观测噪声w(k)、过程噪声n(k)分别为服从N(0,400)分布的高斯随机噪声，采样时间间隔为1 s，取1-α=0.95，进行100次Monte-Carlo仿真，粒子数量Ns1=1 000。

2.1跟踪精度比较

图2a)给出了三种算法的滤波结果比较，SIR算法在机动较弱的上升段与APF算法以及SQP-PF算法跟踪精度相近。在机动较强的巡航段，SIR算法滤波轨迹“毛刺”较多，机动转弯时刻滤波轨迹与真实轨迹偏离程度较大，APF次之，SQP-PF偏离程度最小。

图2　滤波结果比较

从图2b)、图2c)中可以看出，SQP-PF算法位置误差均方根值比SIR与APF的小。SIR整体误差均方根值起伏较大，稳定性较差，SIR算法重采样后大权值粒子复制次数较高，其对应的粒子相异性也较差，可能导致下一时刻粒子分布过于集中，难以描述目标真实状态，进而出现跟踪误差急剧增大，APF跟踪精度有所提高但对误差突变点改善不大；SQP-PF误差水平相对较小且较为均衡，误差突变点较少。

SIR与APF在重采样过程中删除大量小权值粒子，这些粒子可能是位于下一时刻高似然区域的“潜力粒子”[10]，造成跟踪精度降低；此外，当目标机动时，可能出现样本估计无法提供足够的信息，导致APF引入当前观测方法失效。SQP-PF算法根据粒子复制次数建立约束条件更新的多级优化模型，代替SIR中基于粒子复制次数为权值的简单求和，使用SQP求解引入当前最新观测信息的优化模型，最后滤波结果采样新粒子，在提高跟踪精度的同时避免出现大量“潜力粒子”丢失的问题。

2.2粒子多样性比较

选取k=450 s重采样前三种算法的粒子权值分布进行比较，如图3所示。

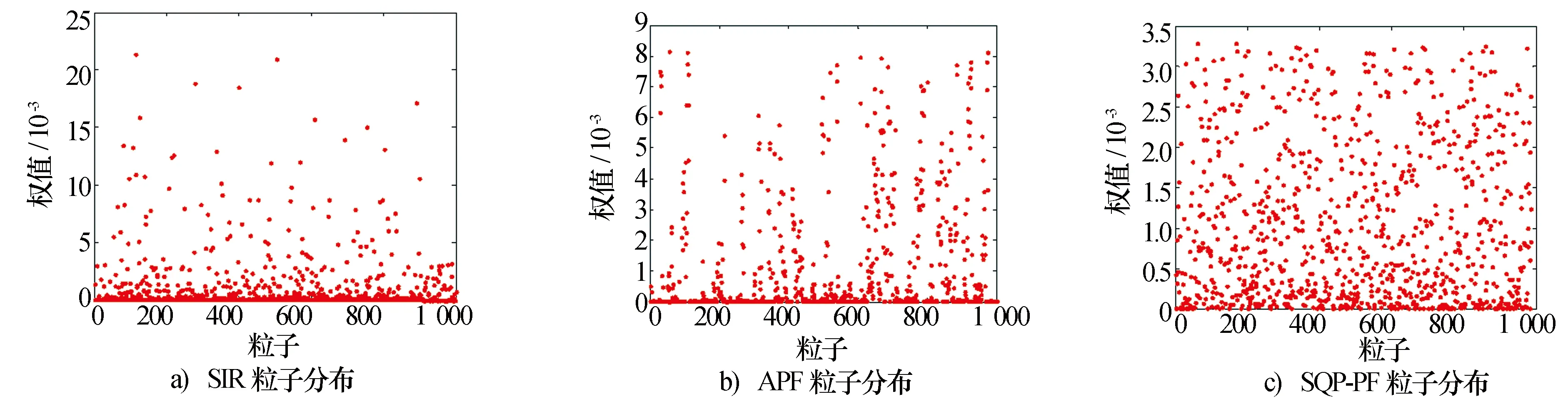
图3　粒子权值分布示意图

由图3可以看出，SIR算法大部分粒子权值趋近于零，粒子退化问题较严重，整体粒子分布差异较大，两极分化严重，极少数的几个粒子点权值很大，造成重采样过程中多次被复制，有效粒子少；APF引入当前观测信息提高了滤波精度，选择高似然性的粒子作为先验对粒子退化有一定的抑制效果，但依然存在较多粒子权值为零；SQP-PF算法在上一时刻只保留不重复的粒子集合U，同时基于滤波结果采样Ns-r新粒子，有效地解决了粒子退化的问题，保证大部分粒子为有效粒子点。

2.3粒子相异性比较

将k=450 s三种算法重采样后的粒子与当前时刻目标真实位置的分布进行比较，如图4所示。

图4　粒子分布示意图

由图4可知，SIR算法在进行450次迭代后，经过重采样粒子重复较多，少数大权值粒子被过度采样，只有少数相异粒子，粒子耗尽问题严重；APF算法粒子主要分布在{(x,y)|x∈[9.88×105, 9.9×105]，y∈[1.3×104, 1.46×104]}之间，粒子多样性有所提高，但粒子过于分散且不均匀，对粒子耗尽问题改善不大；SQP-PF算法粒子分布较为均匀，相异粒子很多，粒子多样性好，在解决粒子退化问题的同时避免出现粒子耗尽问题，粒子质量最好。

2.4总体性能分析

粒子数分别设置为Ns1=1 000，Ns2=800。取α1=0.05，α2=0.1，其他参数取值不变，使用SQP-PF算法进行仿真对比。同时，为比较算法的整体性能，定义以下性能指标：

总体均方差为

(10)

相对误差压缩比为

(11)

平均有效粒子数为

(12)

式中：Mc、Neff_i分别为滤波成功的Monte-Carlo次数、第i次Monte-Carlo仿真实验有效粒子数；ζn(k)、X(k)分别为k时刻滤波值、真实值；t为单次平均滤波时间。

表1给出了SIR、APF以及SQP-PF算法总体性能指标，SIR算法粒子退化较为严重，平均有效粒子数少，导致跟踪失败次数较多。APF使用两次加权处理，解决了SIR对当前量测信息敏感的缺陷，粒子权值变化更加稳定，粒子多样性增强，滤波失败次数减少。SQP-PF算法基于粒子复制次数建立约束条件更新的多级优化模型。引入了最新观测信息，相比SIR和APF跟踪精度更高；其次，利用滤波结果随机采样避免出现粒子溃退问题，平均有效粒子数较大，机动适应能力较强(具体体现在表1中最大误差均方根较小以及图2b)、图2c)中误差尖峰数较少)，滤波失败次数最少。由于SQP-PF算法使用多级优化模型，在SIR基础上增加了粒子排序、多级优化求解以及采样新粒子步骤，滤波耗时较大。

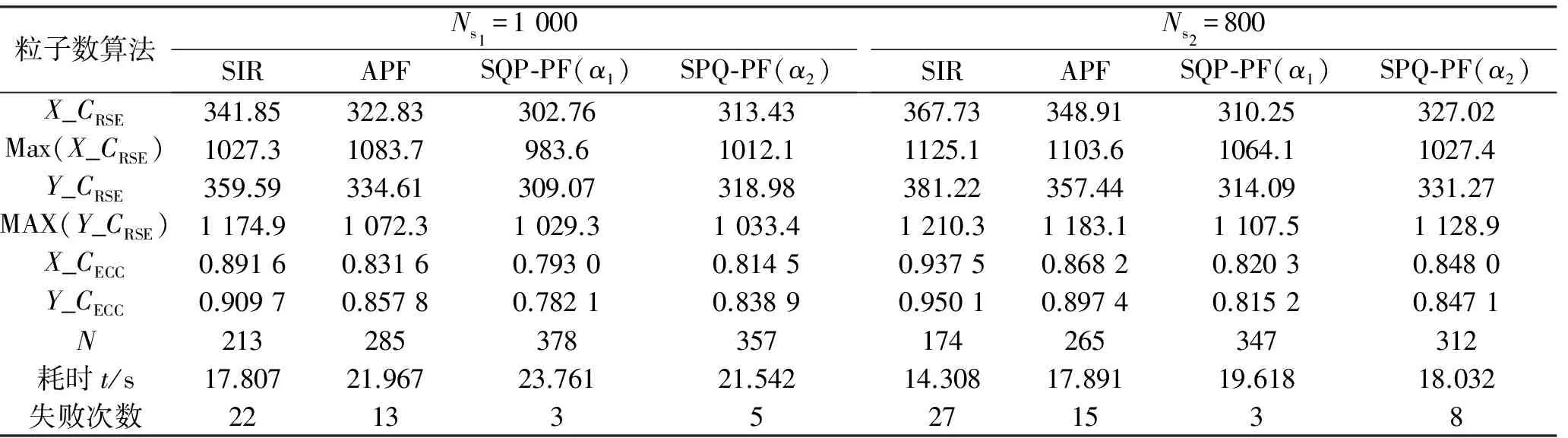
表1　算法总体性能比较

综上所述，SQP-PF算法基于置信水平1-α确定置信区间，筛选区间内粒子进行下一步权值计算，重新分配粒子权值，增加重采样的粒子基数，同时，引入最新观测信息提高了滤波精度，在相同的噪声下，相比SIR与APF算法，SQP-PF整体误差水平较为稳定，突变点少。最后，利用滤波结果采样Ns-r个新粒子，并入集合U作为下一时刻初始粒子，改善粒子质量，避免重采样过程中丢失“潜力的粒子”，根据粒子权值分布可知SQP-PF只有少部分粒子权值为零，重采样后的相异粒子多，分布较均匀，在解决粒子退化问题的同时没有造成粒子耗尽。

3　结束语

本文针对PF存在的问题，提出基于SQP的多级优化PF算法。结合置信水平筛选粒子的思路，减小粒子权值跨度，根据粒子复制次数建立多级优化模型，通过SQP求解引入当前观测信息的参数值，最后，利用滤波结果采样新粒子点，解决了粒子退化问题，此外，补偿因重采样导致小权值的“潜力粒子”被大量删除。仿真结果表明SQP-PF算法跟踪精度、有效粒子数、粒子多样性方面性能优于SIR与APF。从整体滤波时间消耗来看，三种PF算法总体较大，这是PF算法工程实现面临的主要问题之一，由PF粒子计算并行度较高的特点[23-26]，如何通过图形处理器强大的并行数据运算能力实现快速粒子将是下一步研究重点。

[1]李天成, 范红旗, 孙树栋. 粒子滤波理论、方法及其在多目标跟踪中的应用[J]. 自动化学报, 2015, 41(12): 1981-2002.LI Tiancheng, FAN Hongqi, SUN Shudong. Particle filtering:theory, approach, and application for multitarget tracking[J]. Acta Automatic Sinica,2015, 41(12): 1981-2002.

[2]郭云飞, 唐学大, 骆吉安, 等. 一种基于QMC-APF的检测前跟踪算法[J]. 现代雷达, 2015, 37(2): 33-36.

GUO Yunfei, TANG Xueda, LUO Jian, et al. Tracking before detection alogrithm based on QMC-APF[J]. Modern Radar, 2015, 37(2): 33-36.

[3]SABUNCU M, DEMIREKLER M B. IMM-PF for increased performance for maneuvering target tracking[C]// 2001 IEEE 19th Signal Processing and Communications Applications Conference. Antalya: IEEE Press, 2011: 1044-1047.

[4]MIHAYLOVA L, HEGYI A, GNING A, et al. Parallelized particle and Gaussian sum particle filters for large-scale freeway traffic systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2012,13(1): 36-48.

[5]ZHAO Y J, PEI H L. Object tracking based on particle filter with discriminative features[J]. Control Theory Application, 2013, 11(1): 42-53.

[6]LIU Z T, CAO B, SHEN X B. Improved design of proposal distribution for particle filter[J]. Journal of Harbin Institute of Technology (New Series), 2012, 19(6): 72-78.

[7]ZUO J Y, JIA Y N, GAO Q X. Simplified unscented particle filter for nonlinear/non-Gaussian Bayesian estimation[J]. Journal of Systems Engineering and Electronics, 2013, 24(3): 537-544.

[8]LIU C Y, SHUI P L, LI S. Unscented extended Kalman filter for target tracking[J]. Journal of Systems Engineering and Electronics , 2011, 22(2): 188-192.

[9]ZUO J Y, JIA Y N. Particle filter guided by iterated extended Kalman filter[C]// 13th Interational Conference on Control, Automation and Systems. [S.l.]: [s.n.], 2013: 1605-1609.

[10]于洪波, 王国宏, 孙芸, 等. 一种融合UKF和EKF的粒子滤波状态估计算法[J]. 系统工程与电子技术, 2013, 35(7): 1375-1379.

YU Hongbo, WANG Guohong, SUN Yun, et al. Particle filtering algorithm of state estimation on fusion of UKF and EKF[J]. Systems Engineering and Electronics, 2013, 35(7): 1375-1379.

[11]LIN F, WANG H, WANG W, et al. Vehicle state and parameter estimation based on dual unscented particle filter algorithm[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014, 31(5): 568-575.

[12]赵光琼, 陈绍刚, 付奎, 等. 基于变尺度变换减少Sigma点的粒子滤波算法研究[J]. 自动化学报, 2015, 41(7): 1350-1355.

ZHAO Guangqiong, CHEN Shaogang, FU Kui, et al. A particle filter algorithm based on scaled UKF with reduced Sigma points[J]. Acta Automatic Sinica, 2015, 41(7): 1350-1355.

[13]左军毅, 张怡哲, 梁彦. 自适应不完全重采样粒子滤波器[J]. 自动化学报, 2012, 38(4): 647-651.

ZUO Junyi, ZHANG Yizhe, LIANG Yan. Particle filter based on adaptive part resampling[J]. Acta Automatica Sinica, 2012,38(4): 647-651.

[14]陈志敏, 薄煜明, 吴盘龙, 等. 混沌粒子群优化粒子滤波算法[J]. 电光与控制, 2013, 20(1): 36-40.

CHEN Zhimin, BO Yuming, WU Panlong, et al. A chaos particle swarm optimization particle filter algorithm[J]. Electronic Optics & Control, 2013, 20(1): 36-40.

[15]邹国辉, 敬忠良, 胡洪涛. 基于优化组合重采样的粒子滤波算法[J]. 上海交通大学学报, 2006, 40(7): 1135-1139.

ZOU Guohui, JING Zhongliang, HU Hongtao. A particle filter algorithm based on optimizing combination resampling[J]. Journal of Shanghai Jiaotong University, 2006, 40(7): 1135-1139.

[16]常天庆, 李勇, 刘忠仁, 等. 一种改进重采样的粒子滤波算法[J]. 计算机应用研究, 2013, 30(3): 748-750.

CHANG Tianqing, LI Yong, LIU Zhongren, et al. Particle filter algorithm based on improved resampling[J]. Application Research of Computers, 2013,30(3): 748-750.

[17]ZUO J Y, JIA Y N, ZHANG Y Z, et al. Adaptive iterated particle filter[J]. Electronic Letters, 2013, 49(12): 742-744.

[18]张琪, 乔玉坤, 孔祥玉, 等. 随机摄动强跟踪粒子滤波算法[J]. 物理学报, 2014, 63(11): 110505.

ZHANG Qi, QIAO Yukun, KONG Xiangyu, et al. Study on stochastic perturbation strong tracking particle filter[J]. Acta Physica Sinica, 2014,63(11): 110505.

[19]ZHANG G Y, CHENG Y M, YANG F, et al. Design of an adaptive particle filter based on variance reduction technique[J]. Acta Automatica Sinica, 2010,36(7):1020-1024.

[20]WAN J N, SHAO Z J, WANG K X, et al. Reduced precision solution criteria for nonlinear model predictive control with the feasibility-perturbed sequential quadratic programming algorithm[J]. Journal of Zhejiang University: SCIENCE C(Computers & Electronics), 2011,12(11): 919-931.

[21]CAO B, MA C W, LIU Z T. Improved particle filter based on fine resampling algorithm[J]. The Journal of China Universities of Posts and Telecommunications, 2012,19(2): 100-106.

[22]邹卫军, 龚翔, 薄煜明. 自适应分层采样辅助粒子滤波在视频跟踪中的应用研究[J]. 光子学报, 2010, 39(3): 571-576.

ZOU Weijun, GONG Xiang, BO Yuming. Adaptive layered-sampling auxiliary particle filter′s research and application in video tracking[J]. Acta Photonica Sinica, 2010, 39(3): 571-576.

[23]XIN Z Q, SHEN X F. A new approach to accelerate IMM algorithm of maneuvering target tracking based on CUDA[C]// 2012 IEEE International Workshop on Electromagnetics, Application and Student Innovation. Chengdu, China: IEEE Press, 2012: 1-3.

[24]李建江, 张磊, 李兴钢, 等. CUDA构架下的灰度图像匹配并行算法[J]. 电子科技大学学报, 2012, 41(1): 110-113.

LI Jianjiang, ZHANG Lei, LI Xinggang, et al. Parallel grey-level image matching algorithm with CUDA[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(1): 110-113.

[25]孙伟平, 向杰, 陈加忠, 等. 基于GPU的粒子滤波并行算法[J]. 华中科技大学学报(自然科学版), 2011, 39(5): 63-66.

SUN Weiping, XIANG Jie, CHEN Jiazhong, et al. GPU-based parallel particle filter algorithm[J]. Huazhong University of Science & Technology (Natural Science Edition), 2011, 39(5): 63-66.

[26]王爱侠, 李晶皎, 王青, 等. 基于多核的并行粒子滤波运动目标跟踪[J]. 计算机科学, 2012, 39(8): 296-299.

WANG Aixia, LI Jingjiao, WANG Qing, et al. Target tracking based on multi-core parallel particle filter[J]. Computer Science, 2012, 39(8): 296-299.

李凡男，1992年生，硕士研究生。研究方向为临近空间高超声速目标跟踪。

毕红葵女，1964年生，副教授，硕士生导师。研究方向为雷达装备技术及运用。

段敏女，1979年生，讲师。研究方向雷达装备技术及运用。

Particle Filter Algorithm Based on Sequential Quadratic Programming

LI Fana，BI Hongkuib，DUAN Minb，YU Chenlonga，FENG Xiaoa

(a. Department of Graduate Management;b. Department of Land-based Early Warning,Air Force Early Warning Academy,Wuhan 430019, China)

Aiming to the problem that the traditional particle filter does not introduce the current information and the existence of particle degradation, a novel particle filter algorithm based on sequential quadratic programming (SQP) multilevel optimization is proposed. Firstly, based on the characteristic of the residual distribution, a confidence interval is given and used to eliminate the large deviation particles to adjust the particle weights distribution. Then, the re-sampling particle is mapped to set U and a multilevel optimization model is established based on the copy number of each particle, the state parameters of the model are passed out through SQP, the latter optimized value is considered to be the filtering result when the difference of model optimization parameters between before and after stages is less than the threshold. Finally, in order to prevent excessive sampling leading to particle degradation, the filter value and its covariance are used to sample new particles. Simulation results show that the SQP-PF algorithm is superior to the traditional PF algorithm in tracking precision and particle diversity.

particle filter; sequential quadratic programming; multilevel optimization; confidence interval

10.16592/ j.cnki.1004-7859.2016.09.011

国家自然科学基金青年基金资助项目(61401504)

李凡Email：1746338543@qq.com

2016-04-22

2016-06-26

TN957

A

1004-7859(2016)09-0050-07