CS-DOA估计中观测矩阵性能分析
孙晶明
(1. 中国电子科技集团公司 智能感知技术重点实验室, 南京 210039)(2. 南京电子技术研究所, 南京 210039)
·信号处理·
CS-DOA估计中观测矩阵性能分析
孙晶明1,2
(1. 中国电子科技集团公司 智能感知技术重点实验室,南京 210039)(2. 南京电子技术研究所,南京 210039)
利用压缩感知(CS)理论解决阵列信号波达方向角(DOA)估计问题,具有对快拍数据量要求低、可处理相关源等优点。CS-DOA估计中的一个关键问题是构建合适的观测矩阵。文中对比分析了均匀线阵与随机稀布阵两种阵列流形的稀疏重构性能,分析结果表明在实际应用中基于随机稀布阵构建的观测矩阵性能更优。仿真实验从三个方面比较了两种观测矩阵的DOA估计性能,验证了随机稀布阵性能的优越性,在不增加阵元数的前提下,能有效提高阵列的空间角分辨率。
压缩感知;波达方向角估计;观测矩阵;随机稀布阵
0 引 言
随着压缩感知(CS)理论的不断完善与发展,其在阵列波达方向角(DOA)估计领域中的应用也受到了学者的广泛关注,体现出比传统的空间谱估计方法更加优越的性能。CS理论是Donoho、Candès、Romberg和Tao等[1-3]在泛函分析和逼近论的理论基础上,于2004年根据信息论的研究成果建立的。CS理论指出:利用满足一定条件的随机观测矩阵,可将稀疏的高维信号投影到低维的空间,投影后的信号包含了足够的信息,通过非线性的优化方法,便能高概率地重构高维原始信号。DOA估计问题中,空间目标仅占少量空间分辨单元,因此空域目标满足稀疏性约束,结合目标空域稀疏性的DOA 估计算法进而得到了广泛研究。
Cetin和Malioutov等[4-5]最早从2002年开始将稀疏性的思想引入到阵列DOA估计中,通过对空间角度的离散化建立稀疏重构模型,然后利用均匀线阵结合L1-SVD算法对空间目标进行稀疏估计,获得了角度高分辨,但观测矩阵的有限等距性质(RIP)特性较差,且求解算法运算量较大。CS-DOA估计问题的两个要素是:观测矩阵与算法,但现有相关文献都主要侧重于算法研究[6-12],只有少量文献涉及到观测矩阵研究[13-15],且缺少对观测矩阵性能的理论分析。
针对上述问题,本文对比分析了均匀线阵与随机稀布阵两种阵列流形的稀疏重构性能,分析结果表明在实际应用中基于随机稀布阵构建的观测矩阵性能更优,其RIP特性更好,能保证DOA估计的准确性和鲁棒性。
1 CS-DOA估计原理分析
1.1CS基本原理
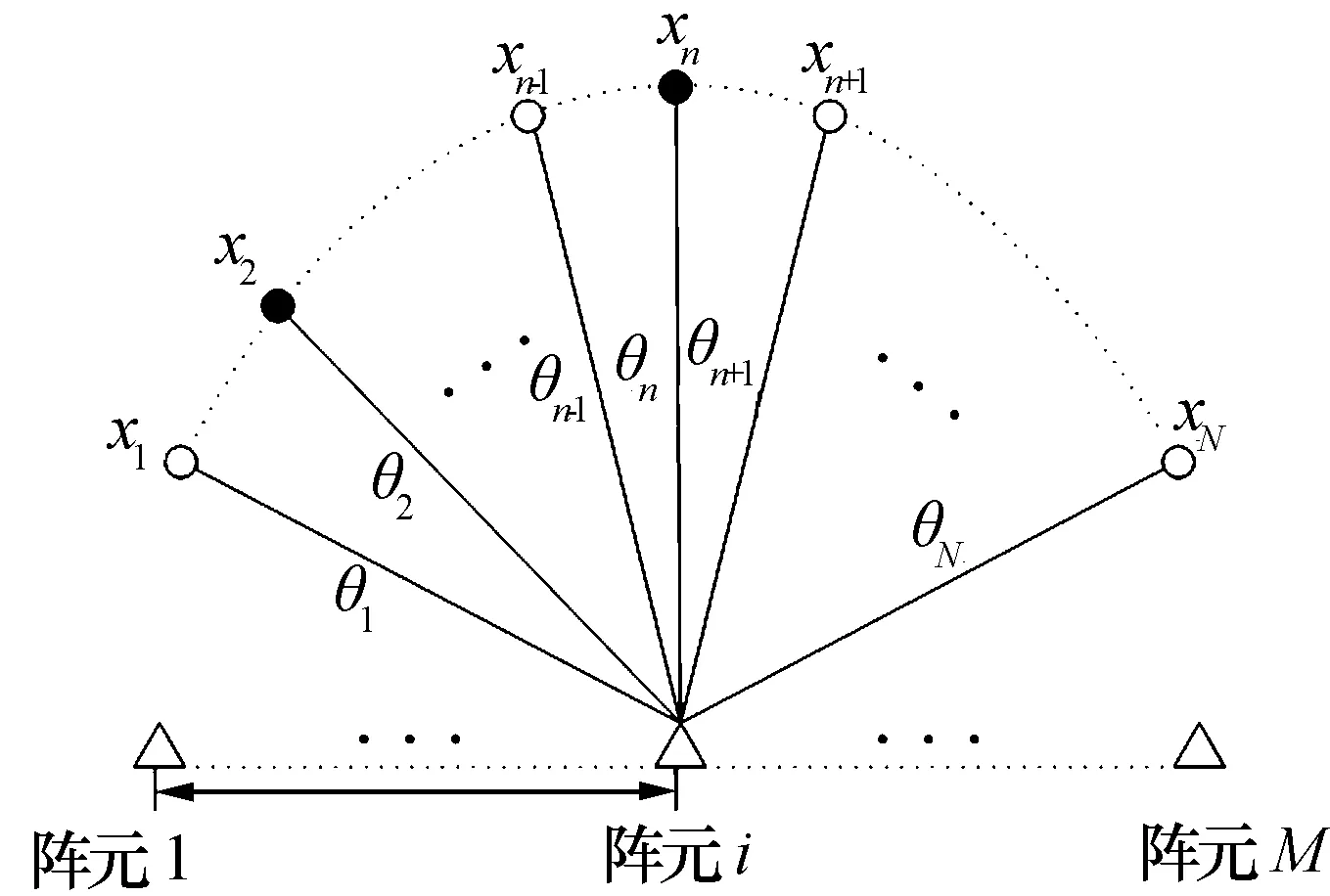
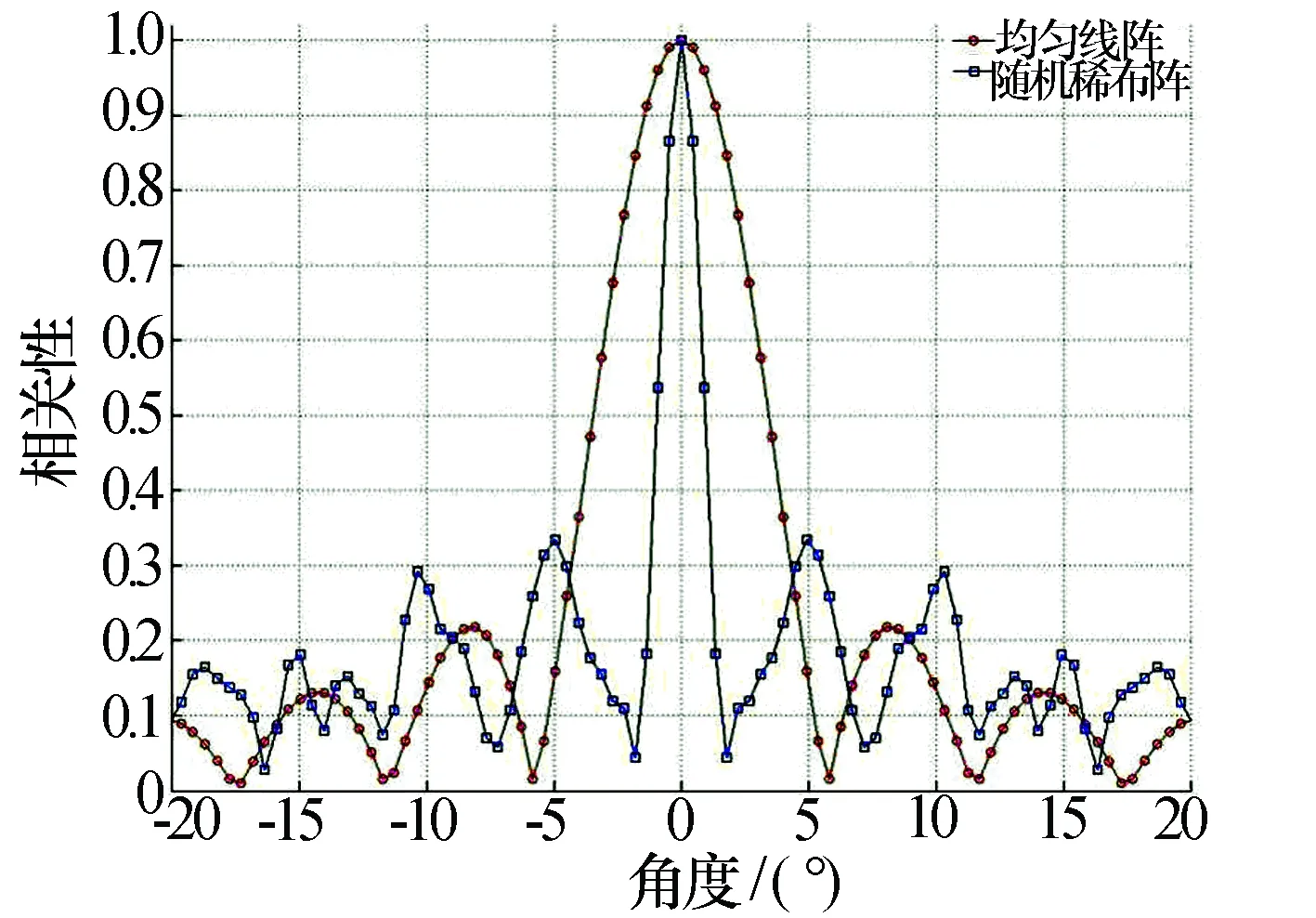
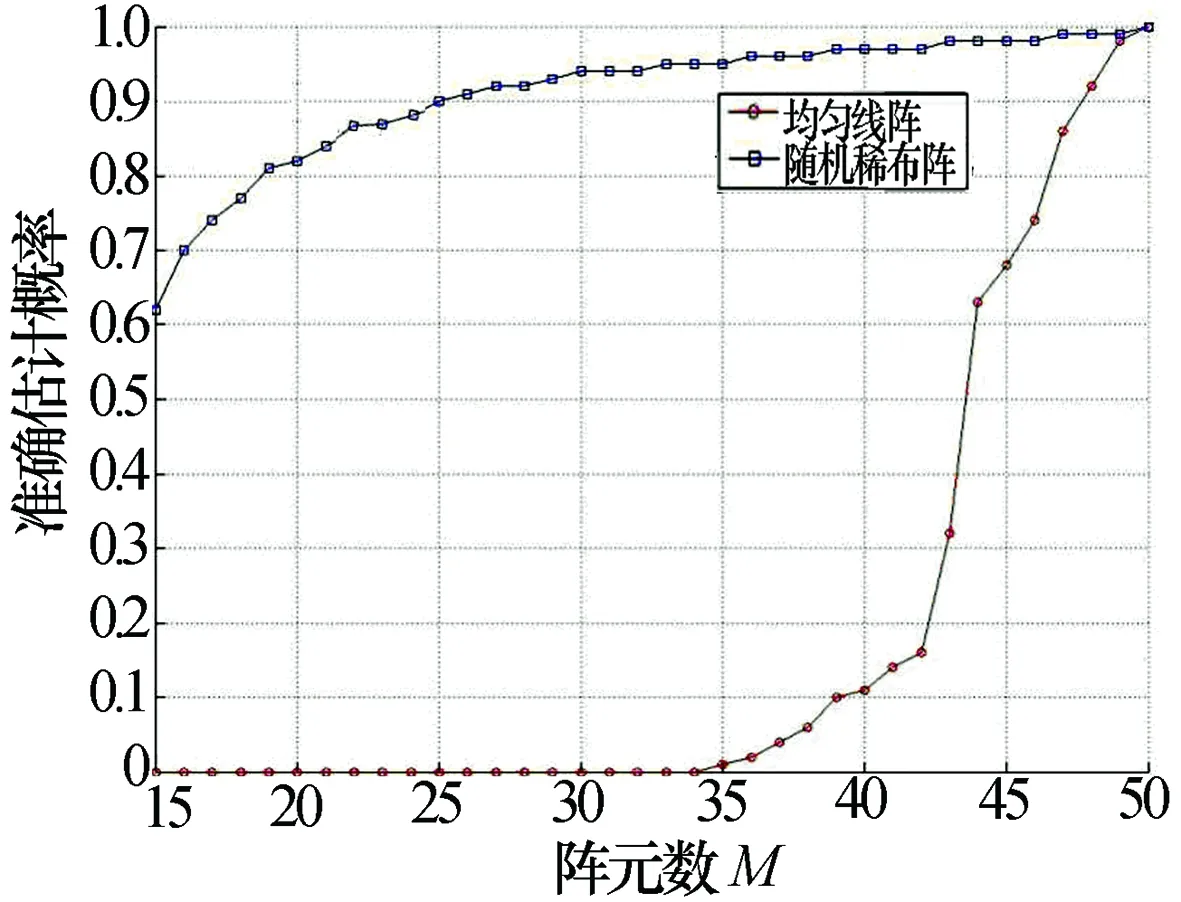
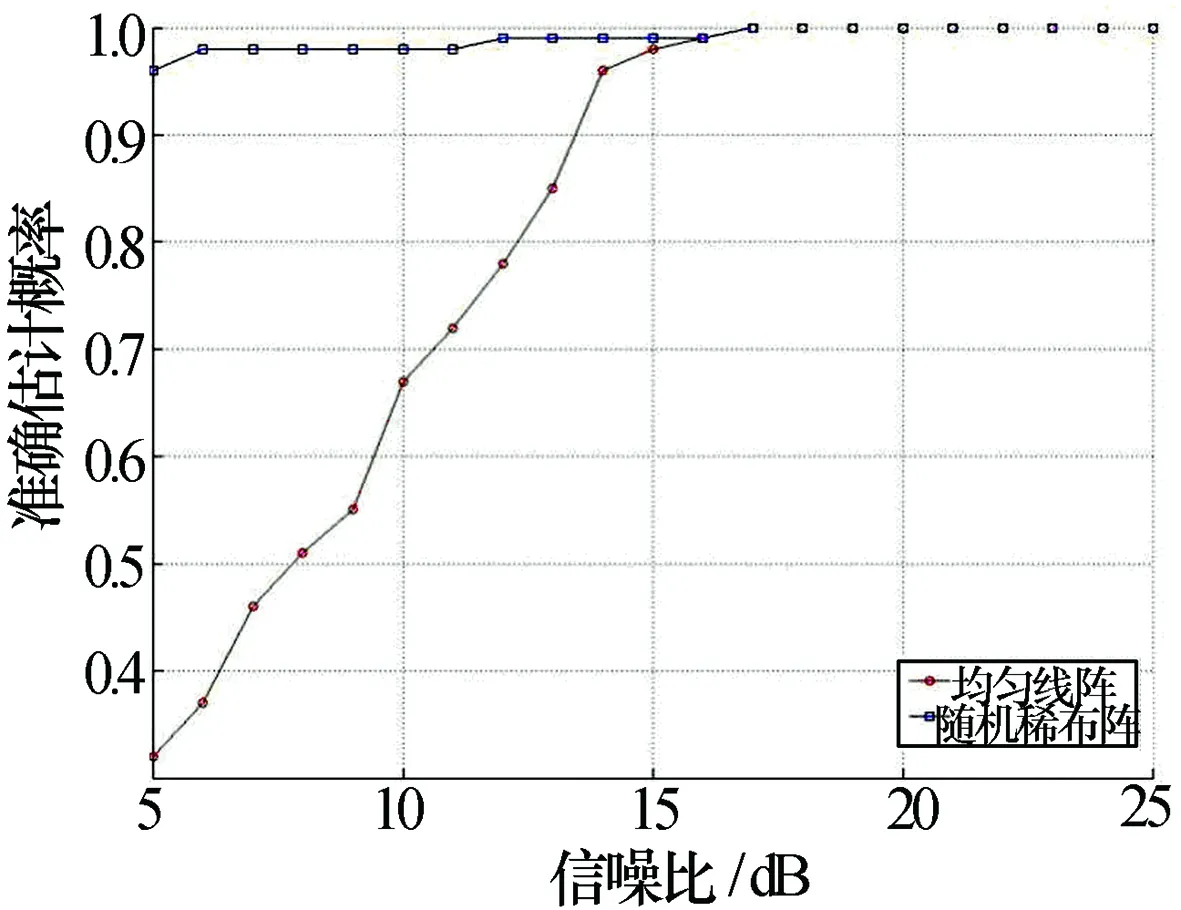
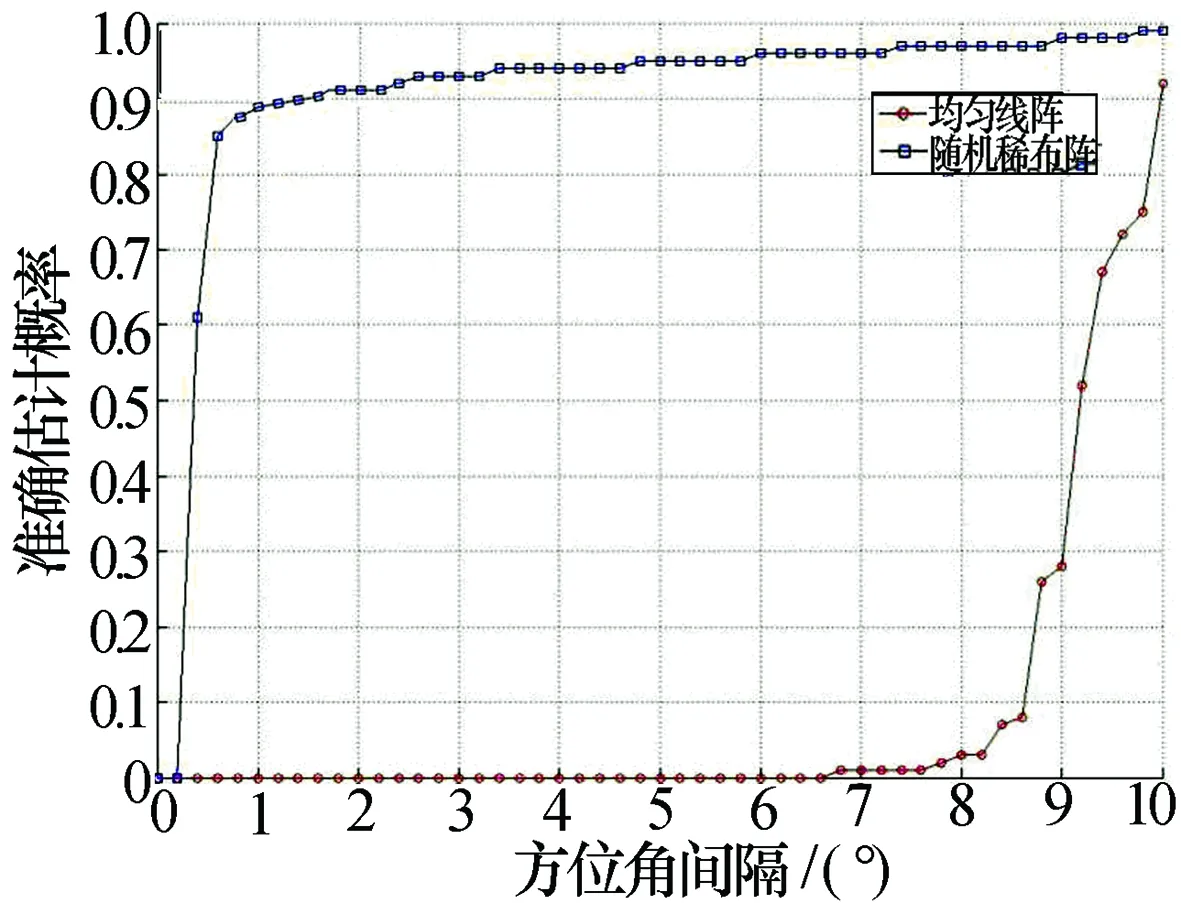
设x是长度为n的信号,稀疏度为k(即x最多含有k个非零值),Φ为m×n阶观测矩阵(m 我们需要求解如下最优化问题 (1) Candès等[2]指出,欲精确恢复k-稀疏的信号x,只要观测值个数m(即y的长度)满足m=O(k·lgn),并且矩阵Φ满足RIP[16]。 然而最小L0范数问题是一个NP难问题,通常需要对该问题加以转化,如将最小L0范数问题转化为最小L1范数问题以方便求解,即 (2) 由于一般的自然信号x本身并不是稀疏的,因此,需要在某种稀疏变换域上对它进行稀疏表示,即x=Ψa,其中,Ψ是稀疏变换矩阵,a是x的稀疏系数向量,且‖a‖0≤k。这时,CS方程为y=Φx=ΦΨa=Θa,其中,Θ=ΦΨ称为恢复矩阵。我们需要求解如下问题 (3) 在实际测量过程中,不可避免地会引入噪声,即y=Φx+n,于是优化求解问题变为 (4) 1.2CS-DOA估计模型 在CS理论框架下研究DOA估计问题,需要对辐射源信号进行稀疏化表示以满足CS理论的前提条件。显然,辐射源信号是自然的空间稀疏信号,采用某种空间网格划分可以实现其稀疏性表示,从而将信号与其空间位置实现一一对应,为从信号重构的角度实现DOA估计提供了依据。这里我们主要讨论利用阵列单快拍接收数据实现CS-DOA估计的问题模型。 设K个远场窄带信号入射到空间某均匀线性天线阵列上,其中,阵列由M个阵元组成,于是该阵列在t时刻接收信号的数学模型为 y(t)=Ax(t)+n(t) (5) 其中,M×K阶阵列流形矩阵A为 A=[a1(ω0)a2(ω0)…ak(ω0)] (6) 导向矢量aq(ω0)(q=1,2,…,K)为 (7) 由此可见,阵列流形矩阵A的每一列对应了一个辐射源信号的空间位置,即阵列流形矩阵包含了辐射源信号的方位信息。 图1 辐射源信号的空域稀疏化表示 将辐射源信号所在空间按方位角划分为{θ1,θ2,…,θN},并假设每一个方位角都对应一个潜在辐射源信号xn(n=1,2,…,N ),如图1所示。图中,“●”表示实际存在的辐射源,“○”表示实际不存在的辐射源。由辐射源信号的空域稀疏性可知,潜在的辐射源个数比实际存在的辐射源个数大得多,即N>>K。这样就构造了一个N×1阶稀疏信号x,且x中只有K个位置有非零元素。于是,DOA估计模型转化为 y=Ax+n (8) 式中:y为某时刻阵列接收的M×1阶信号;x为包含实际辐射源信号的N×1阶稀疏信号;A为信号稀疏化表示后对应的M×N阶阵列流形矩阵,其结构只与布阵规则和空域稀疏化方式有关,而n则代表阵列接收的噪声信号。 利用CS理论来解决DOA估计问题,本质上就是由已知的阵列接收信号y和阵列流形矩阵A来重构稀疏信号x,进而根据x与θ的一一对应关系就能得到辐射源信号的DOA估计。因此,CS-DOA估计问题即转化为求解如下最优化问题 (9) 式中:ε为噪声功率估计值。 至此,我们已经建立了CS-DOA估计模型。根据以上问题描述可知,阵列流形矩阵A相当于CS理论中的观测矩阵Φ。因此,为了精确重构辐射源信号并得到准确的DOA估计,矩阵A需要具备较好的RIP特性。 由于文献[15]已经证明,基于等正弦空间稀疏化方式得到的阵列流形矩阵具有比等角度划分产生的阵列流形矩阵更优越的稀疏重构性能,因此,我们后面的分析都只考虑基于等正弦空间稀疏化方式得到的阵列流形矩阵。 (10) 随机稀布阵与均匀线阵的区别在于其阵元间距不相等,因此,随机稀布阵的阵列流形矩阵可视为均匀线阵的阵列流形矩阵的行随机抽取子阵。 在CS理论框架下,观测矩阵需要满足的稀疏重构条件是RIP准则。从几何角度来讲,RIP准则的要求是待重构的稀疏信号在观测矩阵Φ的作用下必须保持几何性质相一致,即必须保证Φ不会把两个不同的k-稀疏信号投影到同一个采样集合中。然而在实际应用中,判定一个给定的矩阵是否满足RIP是一个NP难问题。因此,一般采用另一个与RIP等价的稀疏重构条件作为判定准则,即:观测矩阵任意两列之间的相关性越小,其稀疏重构性能越强。 定义1[1]:将M×N阶观测矩阵Φ表示为Φ=[Φ1,Φ2,…,ΦN],Φi为Φ的第i列,i=1,2,…,N,则矩阵Φ的相关性定义为 (11) 为便于理论分析,这里给出一定条件下均匀线阵与随机稀布阵的相关性数值对比结果,如图2所示。取M=32,N=401,根据式(10)可得均匀线阵的32×401阶阵列流形矩阵A。为了保证随机稀布阵与均匀线阵的阵列流形矩阵阶数相等,随机稀布阵的阵列流形矩阵B为200×401阶均匀线阵阵列流形矩阵的32×401阶行随机抽取子阵。 图2 两种观测矩阵的相关性对比 从图中可以获得两点信息:(1)由式(11)可知,μ(A)=0.99,μ(B)=0.83,所以μ(B)<μ(A),即随机稀布阵的相关性比均匀线阵的相关性小,反映出随机稀布阵的RIP特性优于均匀线阵;(2)对比两条曲线在0°附近的主瓣3 dB宽度可知,均匀线阵的空间角分辨率约为6°,而随机稀布阵的空间角分辨率约为1.2°。 由此我们可以得到一个结论:随机稀布阵的DOA估计性能优于均匀线阵。下面的仿真实验将验证这一点。 仿真实验将从多个方面比较随机稀布阵与均匀线阵的DOA估计性能,重构算法采用正交匹配追踪(OMP)算法。基本参数设置如下:M×N阶观测矩阵中N=401,即将角度空间按等正弦划分为401个格点;随机稀布阵构建的观测矩阵为200×401阶均匀线阵观测矩阵的M×401阶行随机抽取子阵;辐射源信号个数为3,且幅度均为1。 实验1:不同阵元数M对DOA估计性能的影响。 本实验中,设置阵元数M=15,16,…,50,辐射源信号的方位角分别为-8°, 0°, 8°,信噪比为10 dB。对于每个设定的M,分别进行100次仿真实验,并统计DOA准确估计概率。如图3所示,随着阵元数M的逐渐增加,两种观测矩阵的DOA估计性能都逐渐提高,且随机稀布阵的DOA估计性能明显优于均匀线阵。在阵元数较少(M在30左右)时,均匀线阵无法实现准确的DOA估计,而随机稀布阵仍能保持较高的DOA准确估计概率(超过90%)。 实验2:不同信噪比对DOA估计性能的影响。 本实验中,设置阵元数M=45,辐射源信号的方位角分别为-8°, 0°, 8°,信噪比为5 dB~25 dB。对于每个设定的信噪比,分别进行100次仿真实验,并统计DOA准确估计概率。如图4所示,随着信噪比的逐渐提高,两种观测矩阵的DOA估计性能都逐渐提高,且随机稀布阵的DOA估计性能明显优于均匀线阵。在信噪比较低(5 dB左右)时,均匀线阵较难实现准确的DOA估计,而随机稀布阵仍能保持较高的DOA准确估计概率(超过90%)。 图3 不同阵元数M下DOA准确估计概率 图4 不同信噪比下DOA准确估计概率 实验3:不同方位角间隔对DOA估计性能的影响。 本实验中,设置阵元数M=32,辐射源信号的方位角间隔为0°∶10°,信噪比为15 dB。对于每个设定的方位角间隔,分别进行100次仿真实验,并统计DOA准确估计概率。如图5所示,随着方位角间隔的逐渐增大,两种观测矩阵的DOA估计性能都逐渐提高,且随机稀布阵的DOA估计性能明显优于均匀线阵。在方位角间隔较小(1.2°左右)时,均匀线阵无法实现准确的DOA估计,而随机稀布阵仍能保持较高的DOA准确估计概率(超过90%)。本实验也验证了图2所示的两种观测矩阵的空间角分辨能力,且说明基于随机稀布阵的DOA估计具有更强的鲁棒性。 图5 不同方位角间隔下DOA准确估计概率 通过以上各组实验结果对比可知,基于随机稀布阵构建的观测矩阵的DOA估计性能明显优于均匀线阵,而且在阵列的设计实现上具有更大自由度,具有更加优越的抗噪性和更高的空间角分辨能力。 本文针对CS-DOA估计中的观测矩阵构建问题,从观测矩阵相关性和空间角分辨能力两方面,对比分析了均匀线阵与随机稀布阵两种阵列流形的稀疏重构性能,分析结果表明在实际应用中基于随机稀布阵构建的观测矩阵性能更优,其RIP特性更好。仿真实验从多个方面比较了两种观测矩阵的DOA估计性能,验证了随机稀布阵性能的优越性,能保证DOA估计的准确性和鲁棒性,且在不增加阵元数的前提下,能有效提高阵列的空间角分辨率。 [1]DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [4]CETIN M, MALIOUTOV D M, WILLSKY A S. A variational technique for source localization based on sparse signal reconstruction perspective[C]// Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. [S.l.]: IEEE Press, 2002. [5]MALIOUTOV D M, CETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source loca1ization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022. [6]MODEL D, ZIBULEVSKY M. Signal reconstruction in sensor arrays using sparse representation[J]. Signal Processing, 2006, 86(3): 624-638. [7]TZAGKARAKIS G, MILIORIS D, TSAKALIDES P. Multiple measurement bayesian compressed sensing using GSM priors for DOA estimation[C]// Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. [S.l.]: IEEE Press, 2010: 2610-2613. [8]JONG M K, OK K L, JONG C Y. Compressive MUSIC: revisiting the link between compressive sensing and array signal processing[J]. IEEE Transactions on Information Theory, 2012, 58(1): 278-301. [9]HYDER M M, MAHATA K. Direction-of-arrival estimation using a mixed L2,0 norm approximation[J]. IEEE Transactions on Signal Processing, 2010(58): 4646-4655.[10]WANG J, HUANG Z, ZHOU Y. Direction-of-arrival estimation based on joint sparsity[J]. Sensors, 2011(11): 9098-9108. [11]王超宇, 朱晓华, 李洪涛, 等. 一种鲁棒的压缩感知高分辨率DOA估计方法[J]. 宇航学报, 2014, 35(5): 590-596. WANG Chaoyu, ZHU Xiaohua, LI Hongtao, et al. A robust high-resolution DOA estimation algorithm based on compressive sensing[J]. Journal of Astronautics, 2014, 35(5): 590-596. [12]王秀红, 毛兴鹏, 张乃通. 基于CS的脉冲压缩雷达单快拍DOA估计[J]. 系统工程与电子技术, 2014, 36(9): 1737-1743. WANG Xiuhong, MAO Xingpeng, ZHANG Naitong. Single-snap DOA estimation based on compressed sensing in pulse compression radar system[J]. Systems Engineering and Electronics, 2014, 36(9): 1737-1743. [13]贺亚鹏, 李洪涛, 王克让, 等. 基于压缩感知的高分辨DOA估计[J]. 宇航学报, 2011, 32(6): 1344-1349. HE Yapeng, LI Hongtao, WANG Kerang, et al. Compressive sensing based high resolution DOA estimation[J]. Journal of Astronautics, 2011, 32(6): 1344-1349. [14]王桂良, 郑辉, 路友荣, 等. 基于压缩感知的新型DOA估计算法[J]. 电信技术研究, 2012(6): 7-13. WANG Guiliang, ZHENG Hui, LU Yourong, et al. A new DOA estimation algorithm based on compressed sensing[J]. Research on Telecommunication Technology, 2012(6): 7-13. [15]林波, 张增辉, 朱炬波. 基于压缩感知的DOA估计稀疏化模型与性能分析[J]. 电子与信息学报, 2014, 36(3): 589-594. LIN Bo, ZHANG Zenghui, ZHU Jubo. Sparsity model and performance analysis of DOA estimation with compressive sensing[J]. Journal of Electronics & Information Technology, 2014, 36(3): 589-594. 孙晶明男,1984年生,博士,工程师。研究方向为压缩感知,雷达成像与目标识别,雷达信号处理。 Performance Analysis of Measurement Matrices in CS-DOA Estimation SUN Jingming1,2 (1. Key Laboratory of Intelli Sense Technology, CETC, Nanjing 210039, China)(2. Nanjing Research Institute of Electronics Technology,Nanjing 210039, China) The method of direction-of-arrival (DOA) estimation of array signals based on compressed sensing (CS) theory has advantages such as fewer snapshots requirement and the capacity of dealing with the coherent sources. One of the key issues of CS-DOA estimation is to construct an appropriate measurement matrix. A comparative analysis about the sparse recovery performance of two kinds of array manifold named uniform linear arrays and random thinning arrays is provided in this paper, and the analysis result shows that the performance of measurement matrices constructed by random thinning arrays is better in practical applications. Finally, in the simulation experiments the DOA estimation performance of the two kinds of measurement matrices is compared from three respects, and the advantage of the performance of random thinning arrays is verified that without increasing the number of array elements, random thinning arrays can improve the spatial angular resolution effectively. compressed sensing; direction-of-arrival estimation; measurement matrices; random thinning arrays 10.16592/ j.cnki.1004-7859.2016.09.010 孙晶明Email:sjm@hust.edu.cn 2016-04-26 2016-06-28 TP971.1 A 1004-7859(2016)09-0046-04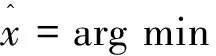
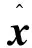
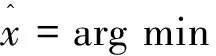


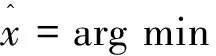
2 观测矩阵性能分析
3 仿真实验结果
4 结束语

