天气雷达降水回波信号特征研究

张振仟，胡明宝，2，孟　鑫，魏　浩

(1. 解放军理工大学 气象海洋学院,　南京 211101；　2. 南京气象雷达开放实验室，　南京 210008)



·总体工程·

天气雷达降水回波信号特征研究

张振仟1，胡明宝1，2，孟鑫1，魏浩1

(1. 解放军理工大学 气象海洋学院,南京 211101；2. 南京气象雷达开放实验室，南京 210008)

引入偏斜度、峰度、均方差等三个信号特征参数，对天气雷达获取的大量降水回波信号的多普勒频谱进行分析。初步研究结果显示：降水回波信号的多普勒频谱分布与回波谱宽大小有关，当回波速度谱宽大于3.5 m/s时，降水回波信号多普勒频谱与高斯谱偏差较大；当回波速度谱宽小于3.5 m/s时，降水回波信号多普勒频谱与高斯谱非常接近。

天气雷达；信号处理；降水回波信号多普勒频谱；非高斯谱

0　引　言

天气雷达信号处理过程中，通常将降水回波信号多普勒频谱近似为高斯谱进行处理[1]。目前，主要在以下两个信号处理环节应用高斯频谱假设：一是地物杂波滤除，2004年Siggia和Passarelli在发表的文章中系统阐述了一种基于降水回波信号满足高斯分布的地物杂波滤除算法[2]，即自适应高斯模型滤波算法(GMAP算法)，经过十余年的发展，该算法开始得到广泛应用；二是回波谱矩参数估计，主要包括平均径向速度和速度谱宽，因为脉冲对处理算法(PPP)实际应用中表现出的稳定性和高效性，它已成为现阶段天气雷达信号处理中应用最广泛的谱矩参数估计算法[3]。

然而，实际观测显示，降水信号多普勒频谱与高斯分布是有偏差的，而且在一些特殊情况下该偏差表现非常明显。1985年，Janssen和Spek[4]采用频率为5.56 GHz的相控阵雷达对气象目标进行长时间观测，经过对回波信号多普勒频谱进行统计分析后，他们发现的气象回波信号多普勒频谱25%以上与高斯谱偏差较大。2009年Yu, Rondinel和Palmer等[5]科学家对美国新一代天气雷达网中WSR-88D雷达观测的一次超级单体回波数据分析，同样发现存在很多信号多普勒频谱与高斯分布偏差较大的降水回波数据。本文对一次强对流天气过程中收集的大量降水回波数据进行研究，探求影响回波信号多普勒频谱形状的主要因素。

1　量度参数介绍

为了定量分析降水回波信号多普勒频谱形状与高斯分布的差异，本文引入三个随机变量特征参数：即偏斜度、峰度和均方差[6]。

1.1偏斜度

偏斜度，通常表示为回波信号多普勒频谱的归一化三阶中心矩。该参数用来量度多普勒频谱相对均值的偏斜程度，可以用来检验频谱是否对称，是一个无量纲的量。如果偏斜度估计值为0，则表示多普勒频谱对称；如果偏斜度估计值小于0，则表示多普勒频谱右偏；如果偏斜度估计值大于0，则表示多普勒频谱左偏。偏斜度表达式为

(1)

式中：S表示频谱的偏斜度；μ3表示频谱的三阶中心矩；σ表示频谱二阶中心矩，即信号谱宽。

(2)

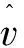
1.2峰度

峰度，通常表示为信号多普勒频谱的归一化四阶中心矩。该参数用来量度多普勒频谱在均值位置附近的峰值特性，可以反映频谱是尖峰或是平顶形状，是一个无量纲的量。对于一个理想的高斯谱，其峰度应该等于3。峰度的表达式为

(3)

式中：K表示频谱的峰度；μ4表示频谱的四阶中心矩。

(4)

1.3均方差

本文中均方差参量，是用来量度回波信号多普勒频谱与其拟合高斯曲线之间的差异程度。需要注意的是，我们通常研究天气信号功率谱高斯分布情况，都是以对数取值进行分析，即功率谱10倍的对数取值，单位为dB或dBm，因此，本文比较功率谱数据与高斯拟合曲线，其实质比较的是其对数值。均方差参量表达式为

(5)

式中：MSE表示功率谱与拟合高斯曲线的均方差；Gl表示第l个采样点的拟合高斯谱的功率值；L表示采样数据的个数。

2　数据选取及处理

本文主要对天气雷达采集的时域I/Q数据进行处理，分析单个距离库降水回波信号功率谱密度分布与其高斯拟合曲线的差异。

2.1数据选取

2013年8月26日8时44分雷达观测体扫数据中包含有强对流降水，考虑到低仰角回波数据通常受地物杂波干扰，文章选取该体扫数据的第二层(即1.5°层)部分数据进行研究。表1显示的是天气雷达主要工作参数。

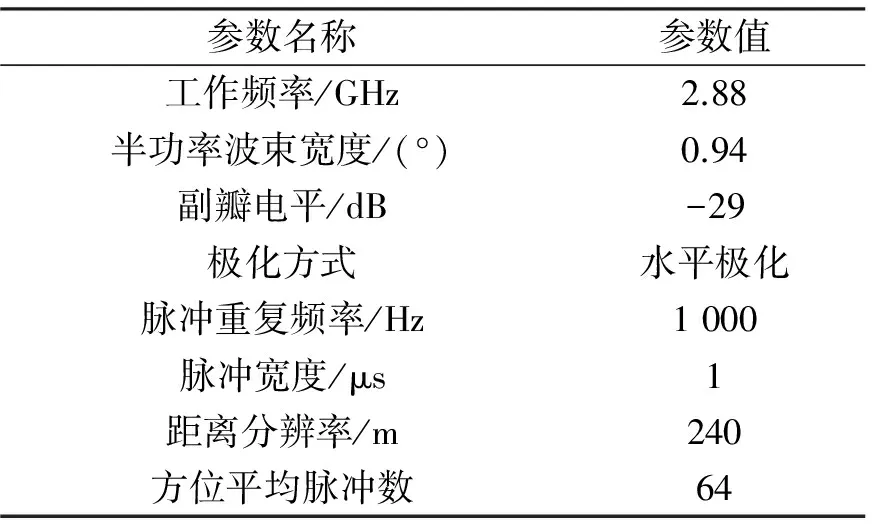
表1　天气雷达主要工作参数

图1显示的是1.5°PPI回波中方位角70°～130°，径向距离50 km～130 km区域附近的局部回波图像，其中，图1a)显示的是反射率因子数据图像，图1b)显示的是速度谱宽数据图像。

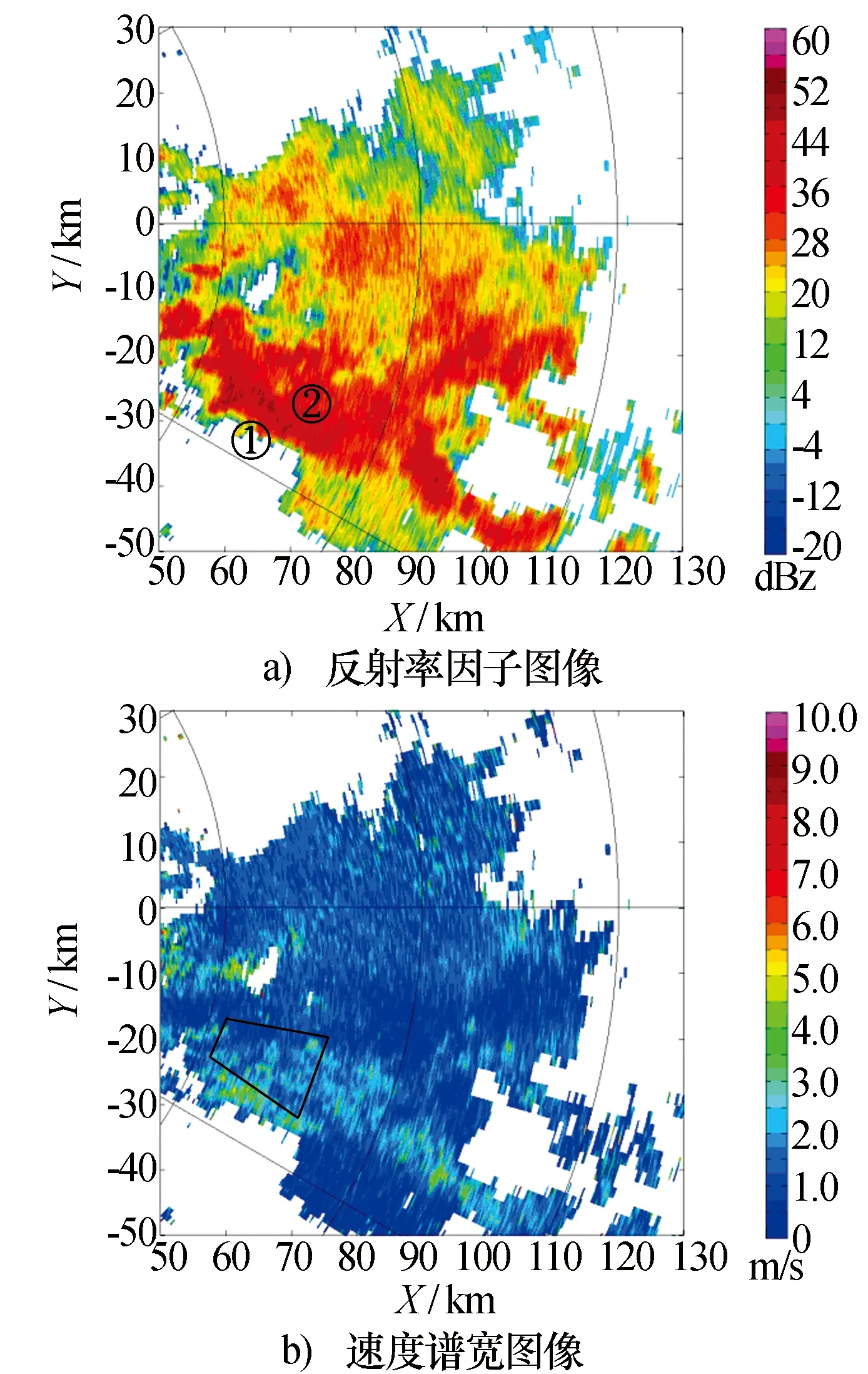
图1　1.5°PPI雷达局部回波图像

2.2数据处理

为了得到降水回波信号的多普勒频谱，本文对获取的I/Q数据直接进行计算。对采样信号sn进行离散傅里叶变换，得到回波信号功率谱密度函数P(k)

sn=In+jQnn=0, 1, 2, 3, …, M-1

(6)

k=0,2,3,…,M-1

(7)

式中：In和Qn分别代表该距离库第n个脉冲回波信号的同相和正交分量；wn表示窗函数(或加权函数)，常用的窗函数有矩形窗、海明窗、布莱克曼窗等，需要注意的是功率谱密度函数要用对数形式表示，单位：dB。

3　数据分析

经过对上述区域数据进行分析，本文发现存在大量降水回波信号功率谱密度分布与高斯分布差异较大的距离库数据，本节分别选取部分距离库非高斯型降水回波信号和高斯型降水回波信号，引入偏斜度、峰度和均方差等三个参数量度降水回波信号频谱与高斯拟合曲线的差异，并初步分析影响回波信号功率谱密度分布的原因。

3.1非高斯型降水回波信号

选取方位角113.7°，径向距离65.04 km～66.24 km六个距离库的I/Q数据(图1a)中①标示位置)进行分析，图2显示的是六个径向上连续的距离库信号的功率谱密度分布曲线及其高斯拟合曲线。需要注意的是，这里得到的高斯拟合曲线，不是对所有功率谱密度值进行拟合，考虑到距离库信号中包含有噪声，本文选取功率谱谱峰位置处的数据点(即纯净的降水回波信号)进行拟合。

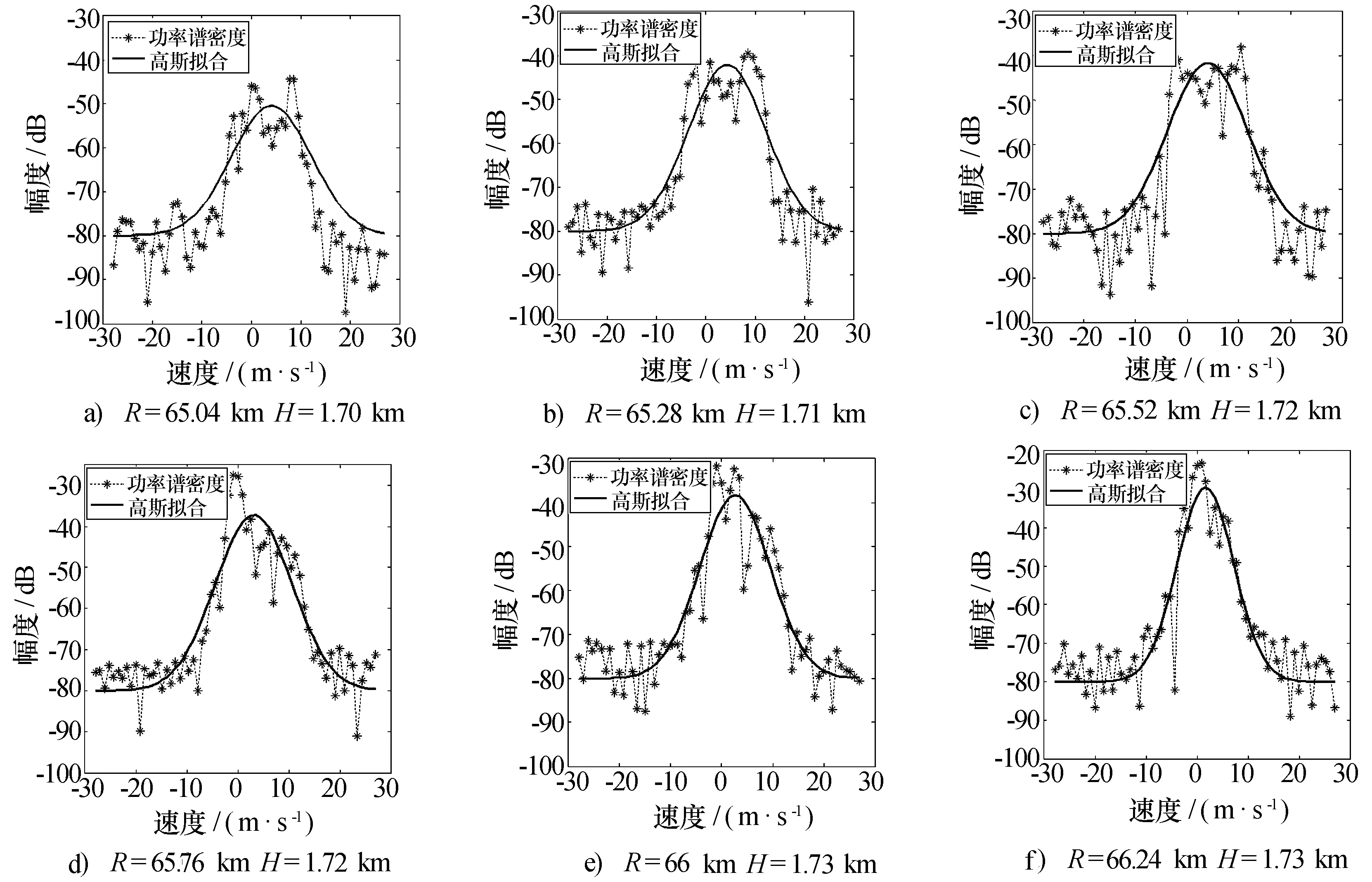
图2　非高斯型功率谱密度分布曲线及其高斯拟合曲线

图2中R表示径向距离，H表示垂直高度。比较功率谱密度曲线与高斯拟合曲线之间的差异，本文得出以下结论：图2a)～图2c)表示的三个距离库降水回波信号的功率谱密度分布曲线与高斯拟合曲线之间差异较大，尤其是谱峰位置，波动比较明显；而图2d)～图2f)三个距离库降水回波信号的功率谱密度分布曲线与高斯拟合曲线的差异相对较小，功率谱密度值基本分布在拟合曲线附近。

为定量分析各距离库降水回波功率谱密度曲线与其高斯拟合曲线之间的差异，本文分别计算出回波信号的速度谱宽、偏斜度、峰度和均方差等四个参数，见表2。

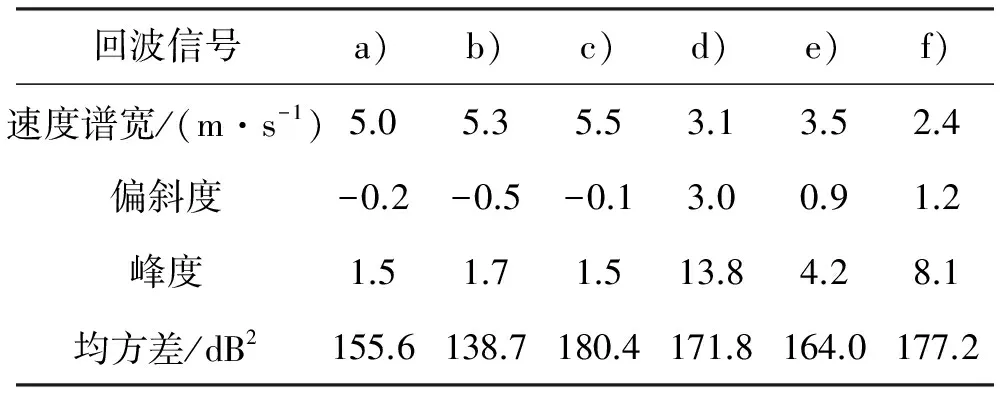
表2　降水回波信号特征参数统计

根据上述参数统计结果，本文得出以下结论：均方差参数显示，六个距离库都大于138 dB2，说明功率谱密度曲线与高斯拟合曲线的差异都比较明显；偏斜度参数显示，图2a)～图2c)三个距离库偏斜度都小于0，表明其功率谱密度曲线稍微向右倾斜，图2d)～图2f)偏斜度都大于0，说明其功率谱曲线稍微左偏；峰度参数显示，图2a)～图2c)三个距离库峰度都小于2，说明其功率谱密度曲线谱峰比较“平”，图2d)～图2f)峰度都大于4，说明其功率谱曲线谱峰比较“尖”；速度谱宽参数显示，图2a)～图2c)速度谱宽比较大，都大于5 m/s，而图2d)～图2f)速度谱宽大于2.4 m/s且小于3.5 m/s。

3.2高斯型降水回波信号

选取方位角112.1°，径向距离66 km～67.2 km六个距离库的I/Q数据(图1a)中②标示位置)进行分析，图3显示的是六个径向上连续的距离库信号的功率谱密度分布曲线及其高斯拟合曲线。R表示径向距离，H表示垂直高度。

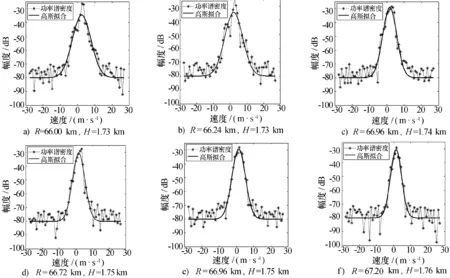
图3　高斯型功率谱密度分布曲线及其高斯拟合曲线

分析图3中距离库功率谱密度曲线与其高斯拟合曲线，本文得出以下结论：相对图2表示的距离库信号，图3表示的距离库降水回波信号的功率谱密度曲线更加接近高斯分布，尤其是图3e)、图3f)。

为定量分析各距离库降水回波功率谱密度曲线与其高斯拟合曲线之间的差异，本文分别计算回波信号的速度谱宽、偏斜度、峰度和均方差等四个参数，见表3。

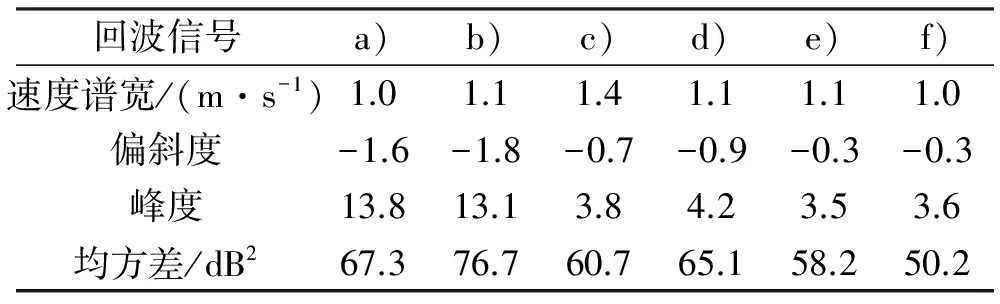
表3　降水回波信号特征参数统计

根据上述参数统计结果，本文得出以下结论：均方差参数显示，六个距离库都小于80 dB2，尤其是图3e)和图3f)，变化度参数小于60 dB2，远小于表2中计算的均方差参数，说明功率谱密度曲线与高斯拟合曲线的非常接近；偏斜度参数显示，图2表示的六个距离库偏斜度都小于0，表明其功率谱密度曲线稍微向右倾斜，其中，图3e)和图3f)偏斜度绝对值小于0.3，说明功率谱曲线对称性非常好；峰度参数显示，图2表示的六个距离库峰度都大于3.5，说明其功率谱密度曲线谱峰比较“尖”，其中图2e)和图2f)的峰度值非常接近3(高斯分布参数值)，说明其功率谱密度曲线形状非常接近高斯分布；谱宽值显示，六个距离库都小于1.4 m/s。

3.3降水回波信号统计分析

选取仰角为1.5°PPI回波中方位角为106°～114°，径向距离为60 km～90 km区间内的降水回波信号(如图1b)中黑色梯形框标记区域的回波，共包含1 250个距离库数据)，进行统计分析。本节根据回波信号的速度谱宽(W)大小，将所选降水回波信号划分为四个区间，分别是0 m/s≤W<1.5 m/s、1.5 m/s≤W<3.5 m/s、3.5 m/s≤W<5 m/s和W≥5 m/s。表4显示的是对四个不同速度谱宽区间降水回波信号的统计结果，包含每个区间包含的数据点数、平均反射率因子、区间内降水回波信号均方差参数的平均值。

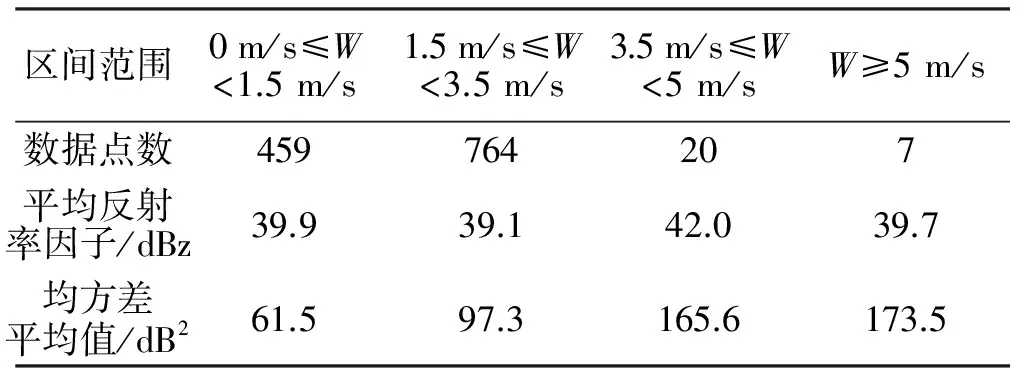
表4　降水回波信号统计结果

根据上述统计结果，本文得出以下结论：所选区域中速度谱宽小于3.5 m/s的降水回波信号占绝大多数，共包含1 223个数据点，速度谱宽大于3.5 m/s的降水回波信号只有27个数据点；四个不同速度谱宽区间降水回波信号的平均反射率因子都大于39 dBz，说明降水回波信号普遍较大，基本可以忽略噪声对均方差参数的影响；均方差参数的统计平均值显示，速度谱宽大于3.5 m/s的降水回波信号的均方差明显大于速度谱宽小于3.5 m/s的降水回波信号的均方差。

4　结束语

本文对天气雷达一次强对流天气过程中时域I/Q数据进行分析，通过引入偏斜度、峰度和均方差等三个参数，定量比较距离库回波信号的功率谱密度分布与高斯分布的差异。根据非高斯型降水回波信号与高斯型降水回波信号的速度谱宽数据，作者认为降水目标谱宽真值大小是影响其回波信号功率谱密度分布的重要因素，当谱宽值较大(大于3.5m/s)时，说明雷达照射体积内降水粒子之间相对运动比较剧烈，此时功率谱密度值分布与高斯分布差异较大，当谱宽值较小(小于3.5m/s)时，雷达照射体积内降水粒子之间相对运动较弱，此时功率谱密度分布可以近似为高斯分布。

文章证明速度谱宽值较大时，在强对流天气过程中存在大量非高斯分布形状的降水回波信号，由于目前大多数信号处理算法研究都是基于高斯分布假设的仿真信号[7-8]，因此，其研究结论对真实天气雷达回波信号不一定完全试用。接下来，我们还需要针对非高斯型降水回波信号对地物杂波滤除、谱矩参数估计等处理过程的影响进行研究。

[1]DOVIAK R J, ZRNIC D S. Doppler radar and weather observations[M]. 2nd ed. New York: Dover, 2006.

[2]SIGGIA A D, PASSARELLI R E. Gaussian model adaptive processing (GMAP) for improved ground clutter cancellation and moment calculation[C]// In Proceedings of 3rd European Conference on Radar in Meteo. [S.l.]: IEEE Press, 2004: 67-73.

[3]斯科尼克. 雷达手册[M]. 3版. 南京电子技术研究所, 译. 北京: 电子工业出版社, 2010.

SKOLNIK M. Radar handbook[M]. 3rd ed. Nanjing Research Institute of Electronics Technology. Trans. Beijing: Publishing House of Electronics Industry, 2010.

[4]JASSEN L H, VAN d S G A. The shape of Doppler spectra from precipitation[J]. IEEE Transactions on Aerospace Electronic Systems, 1985, 21 (2): 208-219.

[5]YU T Y, RONDINEL R R, PALMER R D. Investigation of non-Gaussian Doppler spectra observed by weather radar in a tornadic supercell[J]. Journal of Atmospheric & Oceanic Technology, 2009, 26 (3): 444-461.

[6]胡广书. 数字信号处理[M]. 2版. 北京：清华大学出版社, 2003.

HU Guangshu. Digital signal processing[M]. 2nd ed. Beijing: Tsinghua University Press, 2003.

[7]高志球, 肖艳姣, 袁立功, 等. 天气多普勒雷达回波信号处理的模拟试验[J]. 遥感技术与应用, 1998, 13(4): 43-49.

GAO Zhiqiu, XIAO Yanjiao, YUAN Ligong, et al. A simulation experiment for echo signals from weather Doppler radar[J]. Remote Sense Technology and Application, 1998, 13(4): 43-49.

[8]李妙英, 胡明宝, 贺宏兵. 双极化多普勒天气雷达测速精度的模拟分析[J]. 现代雷达, 2003, 25(12): 32-43. LI Miaoying, HU Mingbao, HE Hongbing. Simulation analysis of dual-polarization Doppler weather radar velocity measurement precision[J]. Modern Radar, 2003, 25(12): 32-43.

张振仟男，1990年生，硕士研究生。研究方向为现代气象雷达技术及其应用。

胡明宝男，1964年生，硕士，教授。研究方向为天气雷达应用。

A Study on Weather Radar Precipitation Echo Signal Characteristics

ZHANG Zhenqian1，HU Mingbao1,2，MENG Xin1，WEI Hao1

(1. College of Meteorolgy and Oceanography, PLA University of Science & Technology, Nangjing 211101 China)(2. Nanjing Open Laboratory of Meteorology Radar,Nanjing 210008, China)

Aiming at analyzing a large number of Doppler spectra of real precipitation signal, introduce three signal feature parameters, including of skewness, kurtosis, and mean square error, the result indicated: the precipitation signal Doppler spectral shape is associated with echo spectrum width, when the velocity spectrum width is more than 3.5 m/s, the Doppler spectra shape is not Gaussian; when the velocity spectrum width is less than 3.5 m/s, the Doppler spectra shape is close to the fitted Gaussian curve.

weather radar; signal processing; Doppler spectrum of precipitation signal; non-Gaussian spectrum

10.16592/ j.cnki.1004-7859.2016.09.003

张振仟Email：zhangzhengqian@qq.com

2016-04-18

2016-06-20

TN959.4

A

1004-7859(2016)09-0012-05