基于Bezier曲线的离心压缩机叶片设计

王友涛　孙洪玉　张磊

基于Bezier曲线的离心压缩机叶片设计

王友涛*孙洪玉张磊

（大连理工大学化工机械与安全学院）（中国特种设备检测研究院）

利用Bezier曲线将子午面型线参数化，设计出满足需要的叶轮子午面型线。在已知叶片进出口安装角和包角的情况下，给出一种基于子午面型线长度的叶片角设计方案。采用CFD方法对所设计的三种离心叶轮进行性能计算，并对比三种叶轮的优劣。通过对比可知，当轮毂叶片角分布采用前部加载式、轮缘叶片角分布采用中间加载式时，叶轮有较好的性能和较均匀的叶片载荷分布。

离心压缩机Bezier曲线叶片角叶轮性能计算

0　引言

离心压缩机叶轮的设计通常可以分为独立的两个阶段。第一阶段为初步设计阶段，利用一维流动分析理论，充分考虑压缩机内部各种损失，结合已有的设计经验，得到叶轮的基本参数。这些参数主要有叶轮进出口宽度、叶轮轴向长度、叶轮入口轮缘轮毂半径和叶片进出口叶片角等。第二阶段为详细设计阶段，给出详细的叶轮流道几何形状以及全流向范围内的叶片角分布。详细设计过程中，设计者需要不断调整叶片和流道的形状，以得到一个既满足性能需求又满足低应力要求的叶轮。

离心压缩机详细设计过程中，如何用参数曲线去表达叶片的几何形状，一直是研究的重点。早期的学者多采用圆锥曲线或圆锥曲线的改进形式去描绘叶片的形状［1-3］。这些方式都不能作为一种通用的叶片形状表达方式，直到Casey给出了一种新的叶片型线定义方法，即利用Bertein-Bezier多项式来定义叶轮流道的形状。利用Bezier曲线来设计叶轮型线有如下优势：叶片曲面是由解析方程定义的，可以系统地对子午面形状加以改进，并且解析方程是可以进行任意次的连续求导；方程的形式简单，可以方便地求得叶片和叶道上点的坐标［4］。这一新的叶片型线定义方法为离心压缩机叶片几何形状设计提供了一种简单而准确的设计方法，从此该方法广泛应用于离心压缩机叶轮的设计中。

离心压缩机叶片角的分布方式对叶轮的性能有着至关重要的影响。在叶片进口角和出口角确定的情况下，叶片角的分布直接地影响叶片表面的载荷分布，进而影响叶道内气体的流动，最终会影响叶轮的性能及其使用寿命。

对于叶片角的设计，叶片角为因变量，自变量一般是轴向相对位置或径向相对位置。当选择轴向坐标值为自变量时，叶片出口附近叶片角沿径向方向梯度变化太大；当选择径向坐标值为自变量时，叶片进口附近叶片角沿轴向方向梯度变化太大。

综上所述，本文提出一种以子午面型线相对长度为自变量的叶片角设计方法。以子午面型线相对长度作为自变量时，全范围内叶片角变化比较平缓，相对易于控制，不会引起叶片结构的突变。

1　叶轮结构设计

1.1叶轮初始参数

Eckardt叶轮是由德国宇航中心设计制造的叶轮，这是一种典型的半开式径向叶轮。德国宇航中心对该叶轮进行了一系列实验，探究了叶轮的性能，获得了叶轮流场的具体细节。由于Eckardt叶轮具有详细的实验资料，长久以来被许多科研工作者当作研究对象。在实验中该叶轮的下游是一个等面积无叶扩压器，其作用是避免叶轮下游的非稳态流动对叶轮内部流动产生影响［5］。叶轮转速最大可达到27 000 r/min，对应的压缩机的滞止压比为7。叶轮为半开式，由铝合金铣成，有20个叶片。由于受离心力作用和材料热膨胀效应的影响，其叶顶间隙是变化的。当转速为0时，叶顶间隙为0.8 mm，达到最大转速时为0.25 mm［6］。叶轮出口安装角为90°。叶轮后部无叶扩压器的径比为2（r3/r2）。表1列出了Eckardt叶轮子午面结构的基本参数。后续的子午面型线和叶片角以此为基础进行设计。1.2子午面型线设计

1.2.1Bezier曲线理论

Eckardt叶轮给出了叶轮进出口的尺寸，却没有给出叶轮子午面轮毂和轮缘的型线。为了下一步叶片角的设计，采用Bezier曲线对轮毂和轮缘型线进行参数化。

表1　Eckardt叶轮子午面结构参数

如图1所示，本文采用五点四次Bezier曲线来描述叶轮子午面型线。Bezier曲线的参数方程为：

图1　五点四次Bezier曲线

当确定了Bezier多边形上五个点（控制点）位置时，即可确定叶轮子午面型线［7］。以子午面轮毂曲线为例，其各控制点位置的求取过程归纳如下：

（1）点0和点4的位置。该两点的位置可以由叶片子午面基本参数确定。所需条件为轮毂半径r1h、叶轮轴向长度以及叶轮出口半径。

（2）点1和点3的位置。根据四次Bezier曲线的性质，多边形的边0-1和边4-3的斜率为曲线端点处的斜率，长度为端点处的ds/du值（曲线弧长s对参数u的伸缩率）的1/4。因此，给定了曲线端点处的斜率，就可给定点1和点3的方向，而给定端点处ds/du不同的值，可使点1和点3沿这两条边滑动，从而在一定程度上改变曲线的形状。实际操作过程中ds/du难以给定，一般通过给定dr/ du或dz/du来代替。

（3）点2的位置。点2的位置影响二端点处的曲率，需要给定两个端点处的曲率。

1.2.2轮毂轮缘型线设计

图2所示为用Bezier曲线设计的叶轮子午面型线。H0、H1、H2、H3和H4为子午面轮毂曲线的控制点，S0、S1、S2、S3和S4为叶轮子午面轮缘曲线的控制点。各控制点的坐标如表2所示。

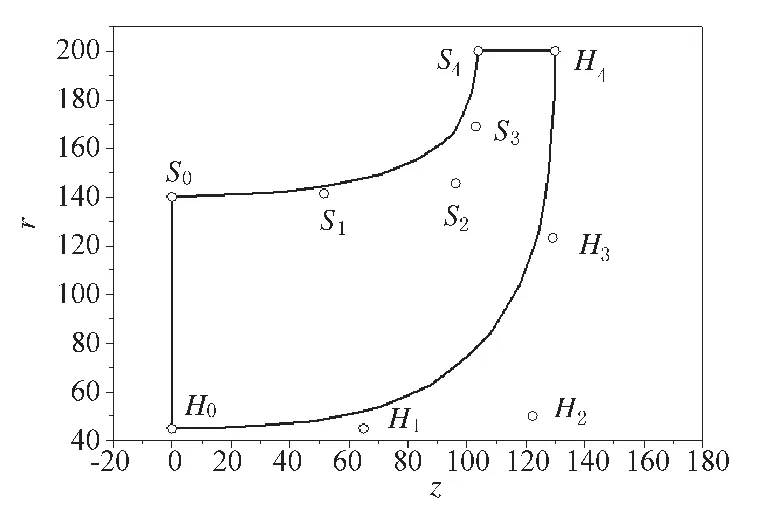
图2　叶轮子午面

表2　轮毂和轮缘型线Bezier曲线控制点坐标

1.3叶片角设计

1.3.1叶片角的定义

图3为离心压缩机叶片角定义图［8］。图3中，坐标系z轴与叶轮中心轴轴线重合。图3（a）中左侧虚线框为离心压缩机叶轮子午流面，每一个子午流面过叶轮轴心，形状尺寸完全相同，描绘了叶轮的截面形状。右侧虚线框为另一个叶轮子午流面，与叶片中型面相交，H是交线上的一个点。实线框为叶片中型面所在的位置，其前缘和初始子午面的叶片入口重合。

M位于轴z上，与H有着相同的轴向坐标。以M为原点，MH为半径作圆弧，该圆弧交叶轮初始子午面于点R，则MH和MR之间的夹角为叶片H点的周向角，记为θi。图3（a）右下角为点H附近的局部图，其中HS为过点H子午面型线的切线方向，而HL为叶片中型面型线的切线方向，HS和HL之间的夹角为叶片角，记为β。而α为HS方向与叶轮轴向（即z向）间的夹角。

图3　离心压缩机叶片角定义

根据lrel的定义方式，可知它的值域为0到1。

图3（b）中Hi和Hi+1为叶片中型面型线上的两点，其距离为dH。对应的子午面上，两点对应的子午面型线距离为dm。而dz为两点在叶轮轴向间的距离。由几何关系可知：

φi+1为Hi和Hi+1两点在周向间的夹角，而ri+1为点Hi+1处的叶轮半径。

1.3.2叶片角的设计

在叶轮基本结构参数确定的情况下，给定叶轮进口和出口安装角β1、β2，则叶轮做功量是一定的。即在此基础上，任意改变叶轮叶片角的分布，叶轮的加功量保持不变［9］。在此理论基础上给出一种叶片角加载方式。

积分叶轮子午流线表达式，可以得到流线的长度l（u）。令流线总长度为l，定义流线相对长度lrel=l（u）/l。可知lrel的值域为（0，1），0对应叶轮进口位置，1对应叶轮出口位置。给定叶轮进口和出口安装角β1、β2，叶片型线上一点对应的叶片角为β，则叶片相对角度的定义为：

由式（4）可知，相对角度βrel的值域为（0，1），叶轮入口处对应βrel=0，出口处对应βrel=1。

图4为四种典型的叶片角分布方式，分别为前部加载式、中部加载式、均匀加载式和后部加载式。不同的叶片角加载方式对应着叶轮内部不同的加功方式。例如，叶片角前部加载方式对应着叶片前部角度变化较大，相应的叶轮加功量也比较大。分别为叶片的轮毂和轮缘选择合适的叶片角加载方式，可使叶片得到良好的叶片角分布。

图4　叶片相对角度加载方式

1.3.3叶片周向角的计算

由图3可知，叶片角β和周向角θ间存在着一定的几何关系。这种关系可以用公式表述成：

由式（5）可知，如果已知叶轮子午面流线（可以是轮毂或轮缘线）上的叶片角分布，则可计算出相应叶片中型面对应的周向角。其求取的积分式为：

式（5）和式（6）中，0和1分别代表子午面流线的进口和出口。而r为叶片角为β的点所对应的叶轮半径值，例如图3中点H处叶片角为β，而线段MH的长度即为其对应的叶轮半径值。

由以上的分析可知，如给定子午面上流线的叶片角分布，可以求出其对应的叶片中型面上对应的叶片型线。其具体的操作步骤可归纳如下：

（1）采用参数化方法对叶轮子午面型线进行设计，如Bezier曲线。在子午面型线上设定若干个计算点，如在Bezier曲线上取自变量u值进行等间距取值，即可将子午面型线划分成多个线段。求取叶轮入口到每一个计算点弧长占子午面型线总长的比例，即可求出各计算点的相对弧长lrel。

（2）按某种叶片加载规律来设计叶片角的分布，得到各个计算点i的叶片角βi。按照图3（b）的几何关系可求取计算点i和计算点i+1之间的周向夹角φi+1。求取公式如下：

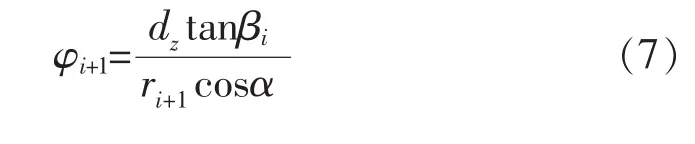
（3）求出了各计算点间周向相对角度后，通过简单的累积求和即可求出叶片型线上点的周向角：

由式（8）即可计算出型线上各离散点的周向角，即可在空间中定位叶片的型线。

1.3.4叶轮模型建立

叶片轮毂处的叶片角分布方式一般采用前部加载式，而轮缘处的加载方式则有多种。在满足轮毂处为前部加载式的条件下，根据轮缘处叶片角分布方式的不同，本文建立三个叶轮模型。这三个叶轮模型的轮缘处叶片角加载方式分别为后部加载式（Ⅰ）、中间加载式（Ⅱ）和均匀加载式（Ⅲ）。叶轮给定叶片厚度为2 mm，入口安装角设定为28°。

2　离心压缩机数值模拟

2.1单通道叶轮网格建立及独立性验证

叶轮模型的网格划分采用turbogrid软件。划分网格的过程中，建立叶轮进口区域和无叶扩压器区域的网格，以便于后续的模拟。图5为叶轮模型（叶轮Ⅰ），图6为叶轮出口处结构网格示意图。

图5　叶轮模型（叶轮Ⅰ）

图6　叶轮出口处结构性网格（叶轮Ⅰ）

计算中叶轮边界条件如图7所示。具体设计如下：（1）叶轮进口条件设置为进口总压101 330 Pa，总温288 K。（2）叶轮出口边界条件设置为流量边界。（3）叶轮部分转速为14 000 r/min，入口部分和扩压器设置为静止，动静区域交界面设置为frozen rotor。作为单叶道模型，入口部分、叶轮部分以及扩压器部分的周向边界设置为周期性边界条件Rotational Periodicity。

图7　叶轮计算模型边界条件设置

对叶轮的数值计算采用单叶道进行计算。在此需要对计算所采用的模型进行网格无关性验证，以保证网格密度不会对数值计算结果产生影响。叶轮采用前述建立的叶轮Ⅰ。根据叶轮网格密度的不同，建立了四个计算模型，分别标记为Ⅰ-Ⅰ、Ⅰ-Ⅱ、Ⅰ-Ⅲ和Ⅰ-Ⅳ。表3记录了四个计算模型不同计算区域网格数。

表3　计算模型网格数记录表

通过数值模拟得到四个计算模型的叶轮性能曲线，如图8所示。由效率曲线可知，四个叶轮的效率曲线在中等流量和小流量范围内基本重合。在大流量范围内，网格数目越多，对应得到的效率值越高。其中叶轮Ⅰ-Ⅲ和叶轮Ⅰ-Ⅳ在全流量范围内效率值相当。

由压比曲线可知，全流量范围内，叶轮总压比随着网格数目的增加而升高。其中叶轮Ⅰ-Ⅳ相对于叶轮Ⅰ-Ⅲ的压比升高的值较小。综上所述，叶轮Ⅰ-Ⅲ的网格数目能够比较准确地描绘叶轮的性能，同时能够节省计算资源。所以选择叶轮Ⅰ-Ⅲ的网格数目作为后续计算的网格划分标准。

图8　叶轮性能曲线

2.2压缩机性能对比

叶轮Ⅰ、Ⅱ、Ⅲ的性能曲线如图9所示。由等熵效率曲线可知，三个叶轮在中间流量处等熵效率基本重合。大流量工况下，叶轮Ⅱ效率略低一些。由总压比曲线可知，全流量工况下，叶轮Ⅱ能获得较大的压比。综合可知，叶轮Ⅱ的性能要优于叶轮Ⅰ和叶轮Ⅲ，特别是在中等流量工况下，叶轮Ⅱ能高效地获得高压比。

图9　叶轮性能曲线

由图10可知，叶轮Ⅱ和Eckardt叶轮在全流量工况下，压比较为接近。低流量工况下，两者非常接近。在流量4.0～6.0 kg/s范围内，压比最大差值为6.3%。

进一步的分析如表4所示，在低流量和中等流量工况下，叶轮Ⅱ和Eckardt叶轮的效率值和总压比的差值都小。大流量工况下，叶轮Ⅱ和Eckardt叶轮效率值和总压比的偏差较大，等熵效率的最大差值为10.6%，总压比的最大差值为6.4%。由以上的分析可知，叶轮Ⅱ和Eckardt叶轮在性能上非常相近，但叶轮Ⅱ的有效工作区域略小。

2．3压缩机叶片载荷对比

图11为叶轮Ⅰ、Ⅱ、Ⅲ在50%叶高处叶片表面静压分布曲线。同一组曲线，位于上方的是压力面静压曲线，下部的为吸力面静压曲线。从图中曲线的分布规律可知，叶轮Ⅰ和叶轮Ⅲ在叶轮流向全程静压分布较为一致，仅在流向后部（0.8～1.0）处吸力面静压分布略有差别。叶轮Ⅱ的静压分布和叶轮Ⅰ、Ⅲ的分布有较大区别。吸力面上，叶轮Ⅱ的静压增长更加均匀，在流向前部（0.15～0.7）其静压值略低于叶轮Ⅰ和Ⅲ，后部（0.7～1.0）其静压值略高于叶轮Ⅰ和Ⅲ。压力面上，在流向位置0.3以前，叶轮Ⅱ的静压值相对要低一些；而在流向位置0.3以后，叶轮Ⅱ的静压值呈直线状态均匀上升，高于其它叶轮；叶片尾缘区域，三个叶轮的静压相当。综合以上的分析可知，叶轮Ⅱ叶片压力面和吸力面压力分布均匀，有更好的叶片载荷分布。

图10　叶轮Ⅱ与Eckardt叶轮的压比曲线

表4　不同工况点叶轮Ⅱ和Eckardt叶轮性能比较

图1150　%叶高下叶片表面静压分布

3　结论

利用Bezier曲线建立了离心压缩机叶轮子午面轮毂和轮缘型线。基于子午面型线相对长度给定了多种叶片角分布方式。建立了三种轮缘叶片角不同分布方式的叶轮模型，对其性能和叶片载荷进行了对比。通过对比可知，当轮毂叶片角分布采用前部加载式、轮缘叶片角采用中间加载式时，得到的叶轮有着较好的性能和较均匀的叶片载荷分布。

［1］Eckardt D.Flow field analysis of radial and backswept centrifugal compressor impellerPart 1：Flow measurements using a laser velocimeter［C］.ASME Conference Publication：Performance prediction of centrifugal pumps and compressor.New Orleans，1980：77-80.

［2］Whitfield A，Atkey R C，Wallence F J.Computer aided design and testing of radial and mixed flow centrifugal impellers with straight and backward-swept blades［J］.I Mech E，1987：21，78.

［3］Krain H.A CAD method for centrifugal compressor impellers［J］.Transaction of ASME，Journal of Engineering for Gas Turbines and Power，1984，106（2）：150-157.

［4］Casey M V.A computational geometry for the blades and internal flow channels of centrifugal compressors［J］. Transaction of the ASME，Journal of Engineering for Power，1983，105：288-295.

［5］Eckardt D.Detailed flow investigations within a highspeed centrifugal compressor impeller［J］.Transactions of the ASME，Journal of Fluids Engineering，1976：390-399.

［6］Eckardt D.Instantaneous measurements in the jet-wake discharge flow of a centrifugal compressor impeller［J］. Transaction of the ASME，Journal of Engineering for Power，1975：337-345.

［7］陈宏冀.子午流道Bezier曲线造型中的几何问题［J］.工程热物理学报，1997，18（4）：445-449.

［8］汪杰.基于UG的压气机叶轮造型系统设计研究［D］.南京：南京理工大学，2013.

［9］秦玉兵，苏莫明.控制加载规律下的离心压缩机叶轮设计方法及数值计算［J］.风机技术，2007（6）：36-39.

Design of Centrifugal Compressor Blade Based on Bezier Curve

Wang YoutaoSun HongyuZhang Lei

Based on the Bezier curve，the streamline of the meridional plane is parameterized and the designed streamline of the meridional plane of the blade meets the requirements.A designing scheme of the blade angle on account of the length of the streamline of the meridional plane is provided while the setting angle of blade and the wrap angle are known.The performance computation is carried out through CFD method on the three different blades and their strengths and weaknesses are compared.The results show that the blade has better performance and more uniform loading distribution when the blade angle of the wheel hub adopts the front loading type and the blade angle of the rim adopts the middle loading type.

Centrifugal compressor；The Bezier curve；Blade angle；Blade；Performance calculation

TH 45

10.16759/j.cnki.issn.1007-7251.2016.10.002

2016-04-15）

*王友涛，男，1989年生，硕士。大连市，116024。