导弹抛底罩过程建模与分析

李慧通， 赵阳， 田浩， 黄意新

哈尔滨工业大学 航天学院， 哈尔滨　150001



导弹抛底罩过程建模与分析

李慧通， 赵阳*， 田浩， 黄意新

哈尔滨工业大学 航天学院， 哈尔滨150001

导弹冷发射采用底罩保护一级发动机，发射后需要将底罩抛离。为了防止底罩撞击地面设备，采用了铰链连接的利用弹簧作为分离能源的侧抛分离方案。对分离运动及动力学特性进行了研究，建立了底罩旋抛过程的运动学和动力学模型。对导弹底罩分离过程中受到的气动力、弹簧力和空气负压力等多种不确定性因素进行了灵敏度分析，通过仿真得到了底罩脱离角度和弹簧相关参数对分离过程的影响，并进行了参数优化。最后对考虑多个偏差影响下的分离方案进行正交仿真试验，得到了主发动机点火时底罩质心散布范围和底罩落点范围。

铰链； 动力学建模； 分离； 灵敏度分析； 仿真

导弹发射过程一般分为冷发射和热发射两种方式。冷发射有两个优点：① 由于发射气流温度低，不会破坏发射系统的结构；② 冷发射相对于热发射系统体积较小，特别适合于车辆、军舰等空间宝贵的运载设备上。其缺点是发射系统复杂程度较高。现阶段潜艇和部分军舰的垂直发射系统以及防空武器发射系统等一般采用冷发射方案。导弹在冷弹发射过程中需要安装底罩来保护主发动机喷管，以防止受到高压发射气体的损坏，弹射到一定高度后需要将底罩抛离，然后主发动机点火，这就对点火时机、点火控制装置技术和点火时弹体的姿态有较高的要求[1]。

目前国内外常用的两种底罩分离方案有：① 侧推方式，首先爆炸螺栓解锁，然后依靠分离弹簧或者推冲器使底罩与弹体远离，分离面之间的距离到达安全距离后侧推发动机开机，使底罩避开导弹的发动机喷流；② 旋抛方式，分离过程中弹体与底罩用铰链机构约束，低冲击分离机构解锁后底罩在压缩弹簧或其他分离能源作用下绕与弹体连接的铰链轴旋转，旋转到设定的角度后铰链机构解锁，底罩在惯性作用下远离弹体，同时避开导弹发动机的喷流[2]。

对于导弹分离过程国内外学者做了很多相关研究[3-10]，Oh等[11]针对采用铰链连接的整流罩分离过程进行了研究，文中采用约束力方程(CFE)法建模，对分离过程进行了仿真，得到了分离体运动结果和约束力变化情况。Tartabini等[12]对分离过程中分离体之间的约束力变化情况进行了分析，推导了两体之间用万向节连接的CFE，并针对X-43A的分离情况进行了仿真研究。Roshanian和Talebi[13]对分离过程中分离体受到的多种不确定性影响因素进行了研究，计算了在多种不确定因素作用下分离体的相对运动轨迹。华楠和阎君[14]提出了底罩整体旋抛分离方案，将底罩和导弹本体用铰链机构进行连接，建立了分离动力学仿真模型，通过仿真和结果分析，验证了尾罩分离方案的可行性。王恒等[15]对弹射出水的飞行器抛尾罩过程中的导向约束段进行了研究，对分离过程中导向销的强度进行了分析，对导向销受到的剪切力、摩擦力等建立数学模型，对比了不同工况下的分离结果。晁锐等[16]提出了一种新型的尾罩分离方案，对罩体与弹体的连接机构、约束机构和滞留机构等进行了设计和仿真验证，提高了尾罩分离的可靠性和安全性，同时降低了成本。贾如岩等[17]对导弹尾罩运动的不确定性进行了分析，采用Mirrors灵敏度分析法得到了多个干扰因素对分离的影响程度，并采用随机打靶方法得到了分离体的运动散布特性。以上研究为底罩旋抛分离方案的研究和仿真提供了参考。

现阶段对采用铰链机构连接的底罩旋抛分离过程的相关研究很少，特别是考虑多种影响因素对分离过程的综合影响情况和对底罩落区范围影响情况。本文针对底罩旋抛分离过程进行分析，研究了设计方案的可行性，采用CFE法建立了分离过程动力学模型，研究了分离方案中的分离角度、弹簧刚度系数和预紧力参数对分离过程的影响，对分离相关参数进行了灵敏度分析，对多种偏差对分离的影响进行正交试验研究。

1　分离方案设计

1.1分离方案

导弹出筒后需立即将底罩抛离弹体，底罩分离过程中必须保证以下几点：

1) 快速性。导弹出筒后必须尽快将底罩抛离，以保证一级发动机按时点火，在点火时必须保证底罩运动到安全区域，如果受发动机喷气流影响太大，则其后续运动规律很难预测。

2) 安全性。底罩落地路线不能撞击到地面或者海面设备，落地点必须在安全区域内。

3) 鲁棒性。分离前导弹姿态和速度存在偏差，分离过程中分离力有偏差，风速对分离过程影响很大，风速大小和方向都难以确定，这需要分离系统具有较高的鲁棒性，在多种偏差作用下能够快速安全分离。

4) 低扰动性。要求分离过程中对上面级弹体姿态扰动较小。

底罩旋抛分离系统主要由底罩、导弹弹体和铰链连接机构3部分组成，如图 1所示。底罩旋抛分离系统具有高可靠性、分离机构简单、分离速度快的特点，能够满足导弹出筒后或者出水后底罩分离的要求。

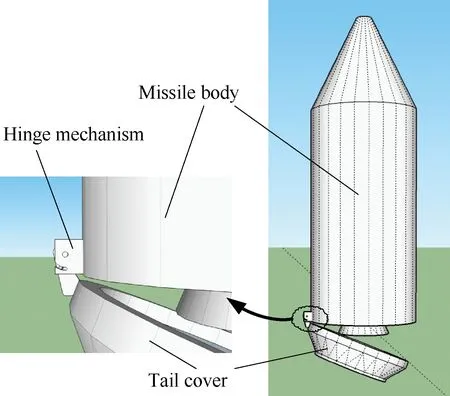
图1　底罩分离方案示意图Fig.1　Diagram of tail cover separation scheme

1.2分离时序设计

当分离命令发出后，低冲击分离机构解锁，底罩在弹簧力的作用下以铰链轴为圆心作圆周运动，此时底罩和弹体之间有铰链约束力。当底罩与弹体达到设计分离夹角时，铰链机构解锁，底罩和导弹弹体成为自由体，导弹主发动机点火继续飞行，底罩则按抛物线规律掉落地面或者海面。图2 为底罩分离过程示意图，分离各阶段可以划分如下：

第1阶段，分离指令发出，低冲击连接分离机构解锁，弹簧开始工作，推动底罩绕铰链旋转，直到弹簧工作结束。

图2　底罩分离过程示意图Fig.2　Diagram of tail cover separation process

第2阶段，弹簧工作结束后，底罩在惯性作用下继续沿铰链旋转，直到到达铰链解锁角度。

第3阶段，铰链解锁后，导弹本体和底罩分为两个自由体，各自作自由运动。

图3为抛罩时序图，导弹出发射筒后不能立即进行底罩分离，导弹出筒瞬间底部受燃气出筒效应影响较大，底部压力场复杂，必须经过t1时间的延迟后才能解锁，t1为0.3 s。连接机构解锁后经过t2时间弹簧工作结束，再经过t3时间铰链解锁，此时弹体和底罩完全分离，约束消失，t2和t3时间不固定，根据设计参数和分离角速度变化而变化。铰链解锁后经过t4时间主发动机点火，从分离开始到主发动机点火总时间为t2+t3+t4=0.7 s。主发动机点火后经过t5时间，底罩落地。

图3　抛罩过程时序图Fig.3　Sequence diagram of tail cover separation process

2　分离过程建模

2.1分离体动力学模型

首先进行模型假设，将底罩分离和分离后的坠落过程进行合理假设，以方便建立动力学仿真模型：

1) 不考虑底罩的弹性变形，将导弹弹体和底罩视为刚体。

2) 考虑分离过程中受到的气动力，特别是阵风对分离过程的影响，大气模型采用美国1976年标准大气模型。

3) 不考虑低冲击分离机构对分离体的冲击影响。

4) 分离过程中导弹姿态控制系统不工作。

5) 由于分离高度较低，不考虑地球曲率的影响。

6) 分离过程中分离体海拔高度变化较小，不考虑海拔高度变化对气动相关参数的影响。

在上述假设的基础上，对导弹底罩旋抛分离过程进行动力学建模。假设分离体在弹体坐标系下的受力为Fx、Fy和Fz，分离体质量为m，飞行速度为u、v和w，转动角速度为ωx、ωy和ωz。在弹体坐标系下平动方程[18]为

(1)

分离体受到的力矩为Mx、My和Mz，转动惯量为I，转动动力学方程为

(2)

式中：

(3)

假设分离体俯仰角为φ、偏航角为ψ、滚转角为γ，则欧拉角与角速度的关系为

(4)

分离仿真计算流程如图4所示，分离命令发出前，底罩和弹体为一个组合体，采用六自由度刚体模型对组合体进行仿真，分离命令发出后分离体解锁，直到铰链机构脱离为止，这一阶段为约束仿真阶段，采用CFE方法计算，当分离面夹角达到设定角度时，判定铰链机构脱离，底罩和弹体分成两个自由体，分别采用刚体动力学计算，合计12个自由度。

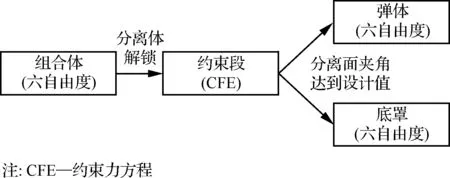
图4　分离仿真计算流程Fig.4　Flow diagram of separation simulation

2.2分离受力分析

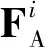
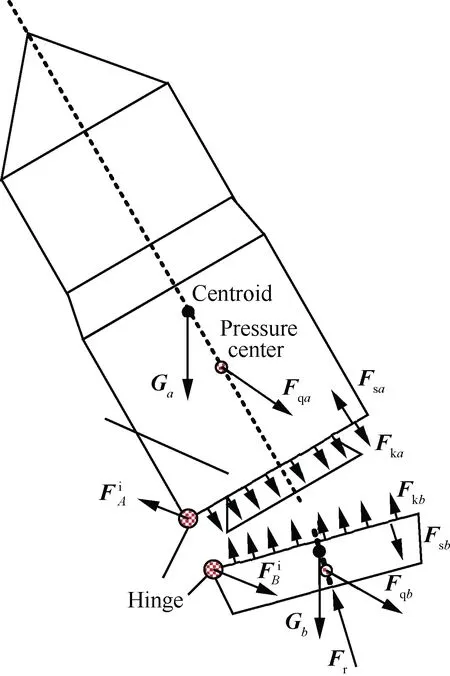
图5　分离受力示意图Fig.5　Diagram of forces during separation

1) 气动力

分离体在运动过程中所受到的空气动力与分离体速度、所在海拔高度的大气密度、分离体外形以及姿态变化有关，在速度坐标系下可以分为阻力Fqx、升力Fqy和侧力Fqz，其表达式分别为

(5)

式中：Cx为阻力系数，Cy为升力系数，Cz为侧力系数，均为无量纲的比例系数；作用在弹体和底罩的气动力与动压q和参考面积Sm成正比，参考面积取导弹的最大横截面的面积，底罩参考面积取底罩上端面面积；动压的表达式为q=ρv2/2，ρ为分离高度的大气密度，v为分离体的飞行速度。气动力矩沿弹体坐标系分解为3个分量，即滚转力矩Mqx、偏航力矩Mqy和俯仰力矩Mqz，气动力矩的计算公式为

(6)

式中：mqx为滚转力矩系数；mqy为偏航力矩系数；mqz为俯仰力矩系数；L为分离体的参考长度。气动系数在分离体外形确定的情况下由风洞试验得到，并形成插值数据表，在仿真时通过攻角α和侧滑角β对气动系数表进行插值，得到每个仿真状态的气动力和力矩系数，进而计算出气动力和力矩。某工况下底罩旋抛分离过程中气动力和气动力矩随分离时间变化情况如图 6所示。

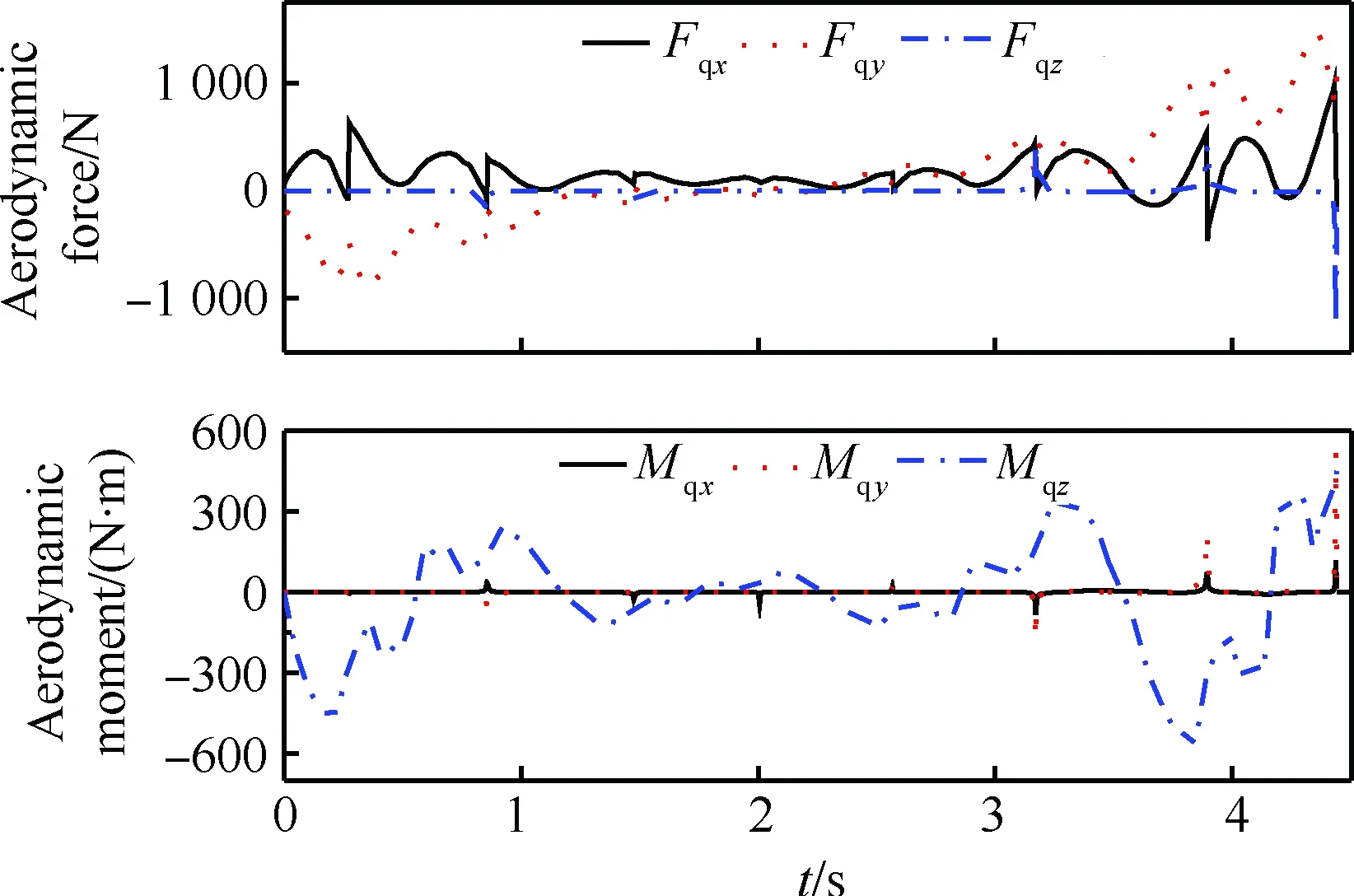
图6　气动力和力矩变化情况Fig.6　Aerodynamic force and moment

2) 风干扰

风干扰对底罩运动的影响较大，风的影响具有地区性和时间性，无法找到其影响规律。仿真过程中将风速与分离体在惯性坐标系下的速度进行整合，得到在风作用下的分离体相对于空气的速度，代入气动力方程进行求解。假设惯性系下分离体速度为V=[VxVyVz]，相对于空气的速度为Vk，风速为Vw，风向角度为δ，当风速与惯性坐标系下X轴正方向重合时风向角度设为0°，以惯性系Y轴为中心，向Z轴方向旋转360°为一周。

(7)

3) 弹簧力

分离能源由压缩弹簧提供，弹簧推力的大小与分离角度相关，弹簧预紧力为Fs0，刚度系数为Ks，阻尼系数为Cs，弹簧作用点与铰链中心点距离为ls，分离体之间夹角为θ，则弹簧的伸长量ds=lscosθ，可以得到弹簧作用于分离体的推力Fs与分离夹角θ之间的关系为

(8)

4) 空气负压与燃气后效

弹体与底罩之间存在密闭空间，分离后分离体相对远离，空间气压下降，外部空气快速进入补充，内部空间气体压强小于外部大气压强，导致产生空气负压力Fk。燃气后效推力Fr是导弹出筒时筒内燃气外泄过程中对底罩产生的残余压力。某分离工况下空气负压力与燃气后效随时间变化情况如图7所示。

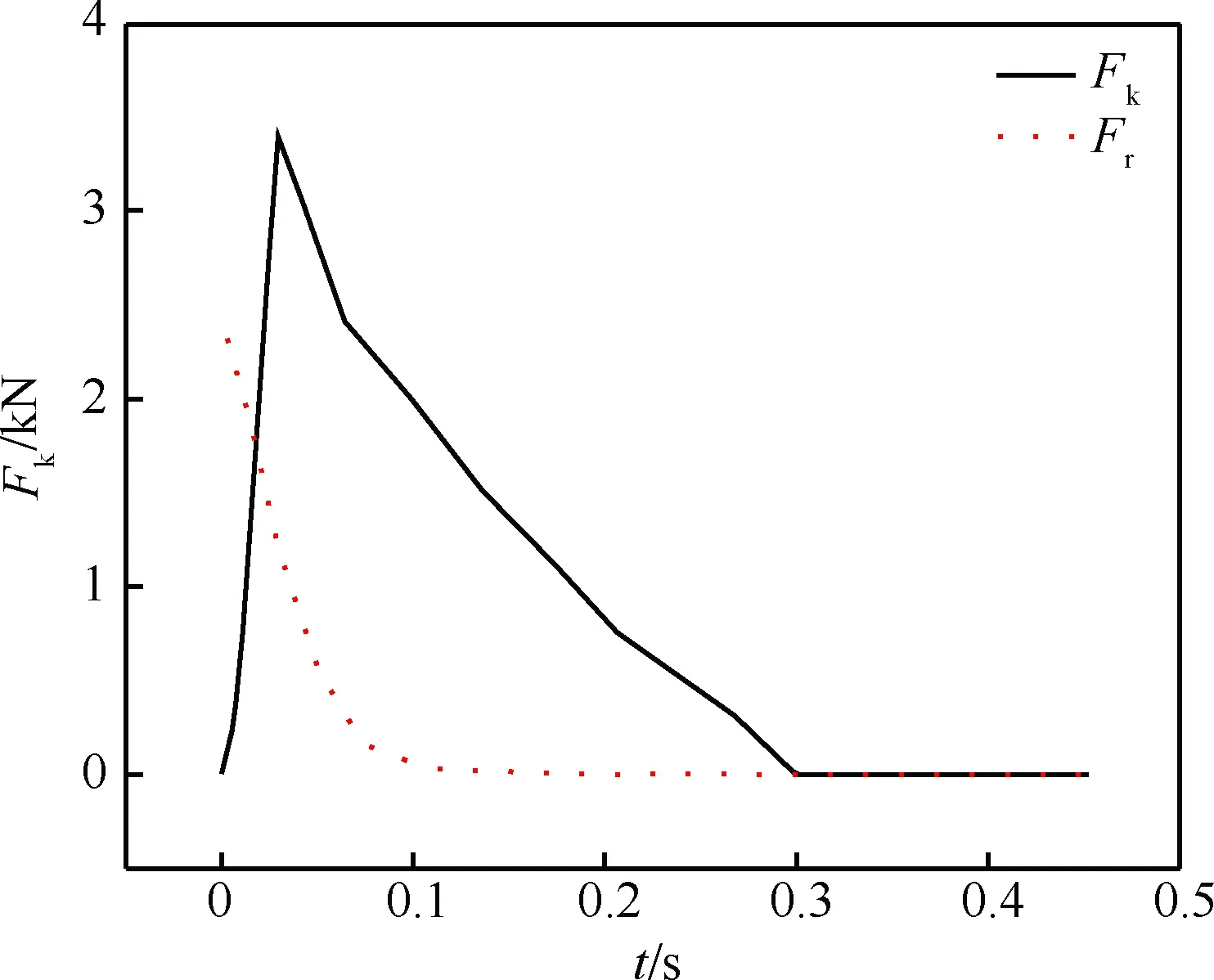
图7　空气负压力与燃气后效变化图Fig.7　Negative air pressure force and exhaust gas after effect

空气负压力作用位置为分离面中心点，作用方向垂直于分离面，力的方向与相对运动方向相反。燃气后效力作用于底罩的底端面，方向沿惯性坐标系垂直向上[19-20]。简化后分离时底罩与弹体围成的空腔压强为Pi，底罩的底端面所受空气和燃气的合压强为Po，空气负压系数为Ck、残余燃气压力系数为Cr，底罩参考面积为Sm，则对分离过程产生的阻力可以简化为

Fzu=Fk+Fr=(PoCr-PiCk)Smcosθ

(9)

3　铰链受力分析

3.1铰链模型简化

铰链机构由支架板、转动板、固定轴和移动轴组成，如图8所示。支架板固定在弹体上，固定轴固定在支架板上，转动板固定在底罩上，移动轴固定在转动板上，移动轴下缘与固定轴中心的距离为Ra。分离过程中转动板压在固定轴上，移动轴在支架板的槽内移动，使底罩绕着固定轴的轴心旋转。

在求解分离铰链系统约束过程中将铰链机构进行简化，简化为一个转轴在支架内旋转的形式，转动板简化为转轴，支架板简化为支架，转轴中心为固定轴的中心，转动轴半径为Ra。当转轴与支架之间的转动角度达到设计分离角时使铰链机构失效，底罩和弹体变成自由体。

3.2分离铰链约束模型

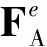
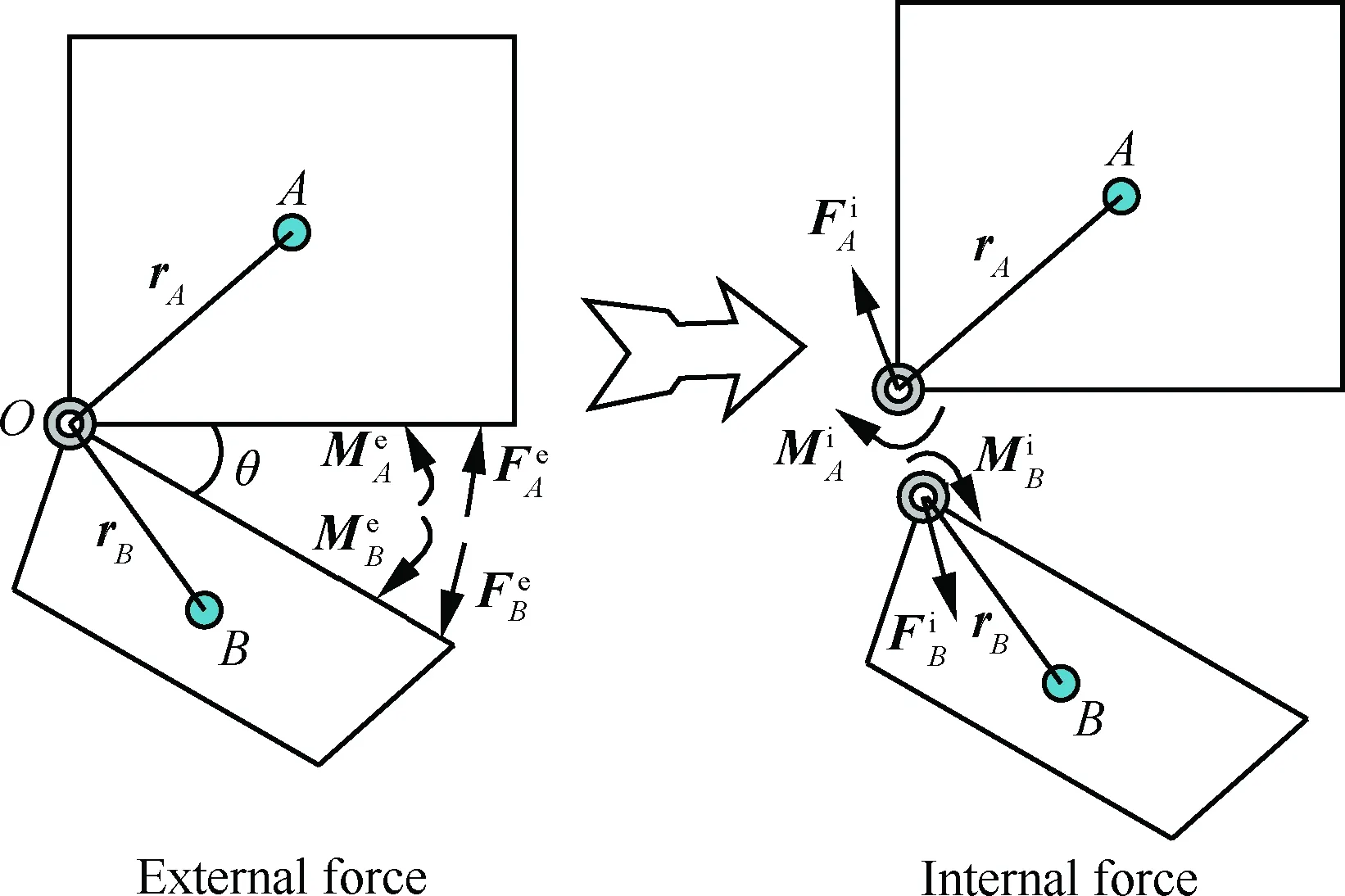
图9　分离体受力分析Fig.9　Forces analysis of separation body

弹体质量为mA，转动惯量为IA，弹体平动和转动动力学方程为

(10)

底罩质量为mB，转动惯量为IB，底罩平动和转动动力学方程为

(11)

由于只有弹体和底罩两个分离体，分离过程中铰链对弹体和底罩的约束力是等值反向的，可以得到

(12)

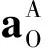
式中：an和at分别为法向和切向加速度，且

(13)

(14)

可以得到铰链连接分离约束方程为

(15)

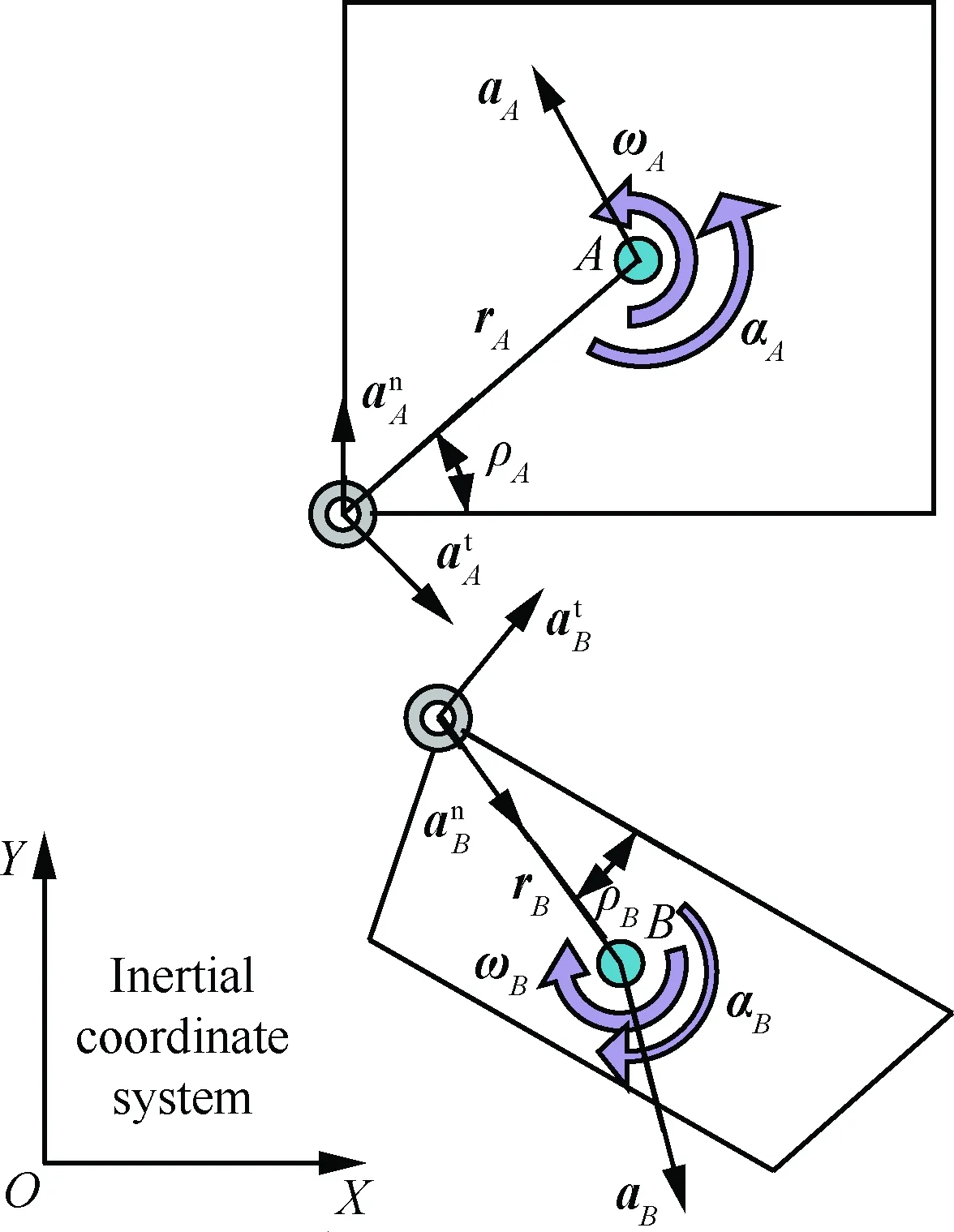
图10　分离体加速度示意图Fig.10　Diagram of separation bodies’ acceleration

联合式(12)～式(15)可得铰链机构约束力的显式表达式为

(16)

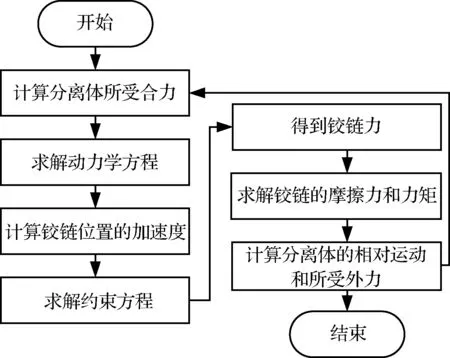
图11　CFE法流程图Fig.11　Flow diagram of CFE method

3.3铰链机构摩擦力

铰链装置产生的摩擦力由两部分组成，上部固定轴与转动板的接触为线接触，下部移动轴与支架板的接触为点接触。具体形式如图 12所示。固定轴中心距离移动轴中心距离为Rc，与移动轴上缘距离为Rb，与移动轴下缘距离为Ra。固定轴与转动板之间的作用力为Nb，移动轴与支架板之间的作用力为Na，Na与Nb通过分离动力学与约束方程解算求出。

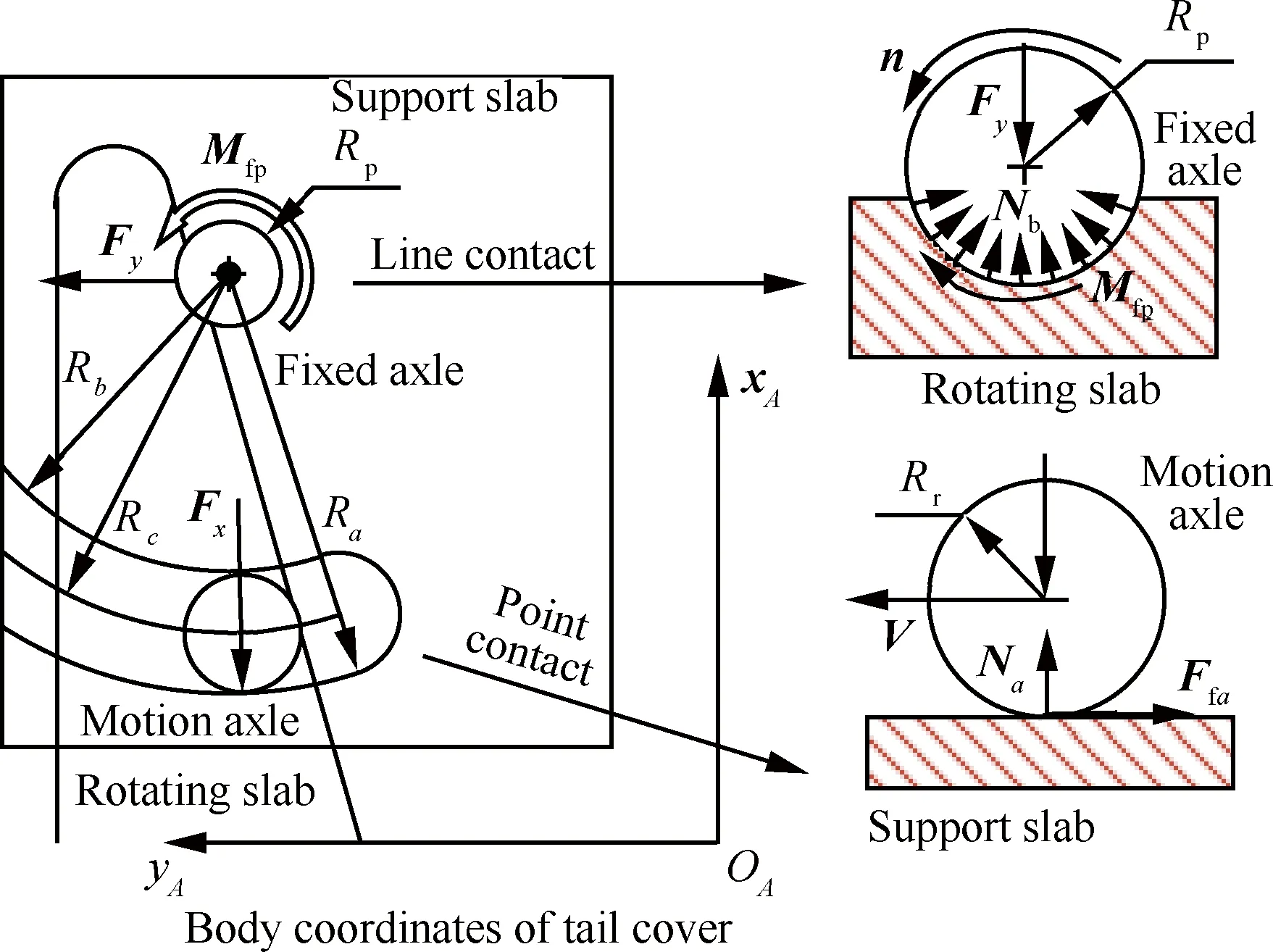
图12　铰链机构摩擦力示意图Fig.12　Diagram of frictional forces of hinge mechanism

点接触形式可以将其横切面等效为一个圆与一个平板接触的形式，fa为库伦摩擦系数，移动轴与支架板的摩擦力为Ffa，对底罩产生的摩擦阻力矩为

(17)

固定轴与移动板接触位置没有间隙，线接触摩擦可以简化为径向轴承摩擦。在跑合情况下同时考虑压力分布和偏转因素对摩擦系数的影响[21]假设固定轴与移动板之间的摩擦系数为f，所得到的当量摩擦系数为

(18)

底罩与固定轴的摩擦力矩[22]为

(19)

式中：n为旋转轴方向；Rp为固定轴的半径长度；铰链阻力矩系数Cjz，默认值为1，铰链对底罩分离产生的摩擦阻力矩为

(20)

4　底罩分离仿真

4.1分离参数设计

分离系统中可设计参数包括分离角Af、弹簧等效刚度系数Ks和弹簧预紧力Fs0这3种，根据以往的经验将设计参数设定为分离角Af=75°， Ks=2.0×107N/m以及Fs0=5.0×105N。调节设计参数的值进行多次仿真，可以得到分离各项指标随设计参数的变化情况。此时设定风速为零，其他干扰因素为理想状态。分离过程中，最重要的指标为主发动机点火时底罩的横移量ΔLa和底罩的落点距离Lb。此外要求主发动机点火时弹体的角度偏移ΔA要小，铰链机构分离时间ts要短。

图13显示了分离角度值对抛罩过程的影响，随着分离角度从40°增加到110°，落点距离先增加后减小，最大值在71°附近，主发动机点火时底罩横移量和弹体角度同样先增加后减小，分离时间则随角度增大而增大。

图14显示，随着预紧力增加，落点距离、底罩横移量和点火时弹体角度增大，分离时间则随着预紧力增加而减小，图中表明预紧力对分离过程影响很大，当预紧力由100kN增加到1 000kN时落点距离由10m增加到50m，但当预紧力增大时对弹体姿态影响也变大，姿态角变化量由0.1° 上升到0.5°，同时过大的预紧力对连接机构的强度要求也相应增加。

图15中，随着刚度系数增加底罩横移量、落点距离和弹体角度下降。分离时间则随刚度系数增加而增加。刚度系数减小时，弹簧机构对分离体作用时间增加，使底罩抛得更远，同时对弹体姿态干扰也加大，刚度系数过小会导致弹簧工作行程过长，不利于分离。

图13　分离角度值对抛罩过程的影响Fig.13　Influence of separation angle on tail cover separation process

图14　预紧力对抛罩过程的影响Fig.14　Influence of preload on tail cover separation process

图15　刚度系数对抛罩过程的影响Fig.15　Influence of stiffness coefficient on tail cover separation process　

底罩分离结果期望落点距离最大，主发动机点火时底罩横移量最大，铰链机构分离时间最小，同时要满足约束条件：主发动机点火时弹体角度与分离时刻相比变化要求小于0.5°，同时分离弹簧工作行程Lsw=Fs0/Ks小于0.2m大于0.05m。

底罩分离系统优化为多目标有约束的非线性优化问题，采用遗传算法进行优化仿真，同时考虑到方便相关器件设计与采购[23]，得到优化后的设计参数为Af=65°，Ks=6.0×106N/m，Fs0=6.0×105N。在某工况下经验计算结果和优化后计算结果对比如表1所示。

表1　设计参数优化结果对比

通过参数优化显著提高了主火箭点火时刻的底罩横移量，增加了落点距离，减小了分离时间。

4.2偏差灵敏度分析

分离过程受到的外部干扰和偏差包括风速Vw影响、风向角δ变化、空气负压系数偏差Ck、残余燃气压力系数偏差Cr、气动阻力系数Cx偏差、气动升力系数Cy偏差和气动侧力系数Cz偏差。这些偏差会导致作用在底罩上的力发生变化，特别是风干扰，其大小和方向随机变化，难以预测。

分离体内部偏差包括弹体坐标系下底罩质心位置偏移Δx和Δz，分离时刻惯性坐标系下弹体速度偏差ΔVx、ΔVy、ΔVz和弹体系下角速度偏差Δωx、Δωy、Δωz，底罩下落高度偏差Δh，弹簧阻尼系数Cs偏差和铰链阻力矩系数Cjz偏差。偏差配置及允许设计范围如表2所示。

对分离过程的各种影响因素进行灵敏度分析，得到各项因素对底罩分离的影响程度如图 16所示，图中横坐标为相关参数编号。由图可知对于底罩的落点位置影响最大的是风向角、风速、分离角度和弹簧预紧力等，对于主发动机开机时底罩横移量影响最大的因素为弹簧预紧力、弹簧刚度系数、分离角度、风速和铰链机构等效摩擦系数等。对弹体角度影响最大的因素为风向角，弹簧刚度系数，弹簧预紧力、铰链阻尼系数和风速。对分离时间影响最大的是分离角度、弹簧刚度系数和预紧力。

表2　分离仿真参数

4.3分离不确定性分析

设计参数确定以后，分离过程中底罩受多种偏差因素的影响，特别是风速和风向角，变化范围大，影响效果明显。图 17为风速对落点距离和底罩横移量的影响。在风方向角为0°时底罩处于逆风飞行状态，随着风速增加，落点距离明显减小，当风速由0 m/s增加到12 m/s时，落点距离由35 m降低到15 m以内，底罩横移距离由5.3 m 降低到4.8 m。

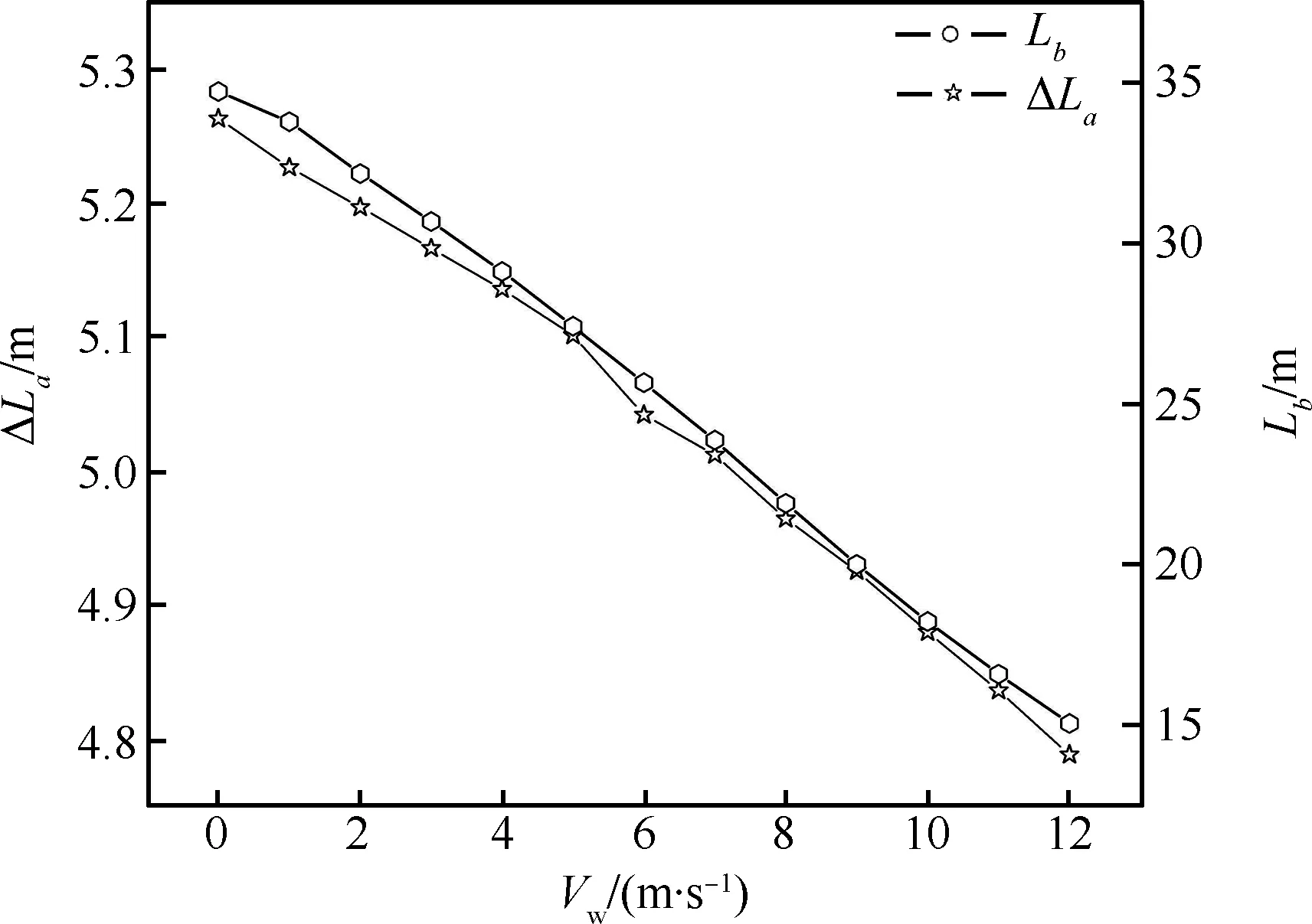
图17　阵风对分离过程的影响Fig.17　Influence of gusts on separation

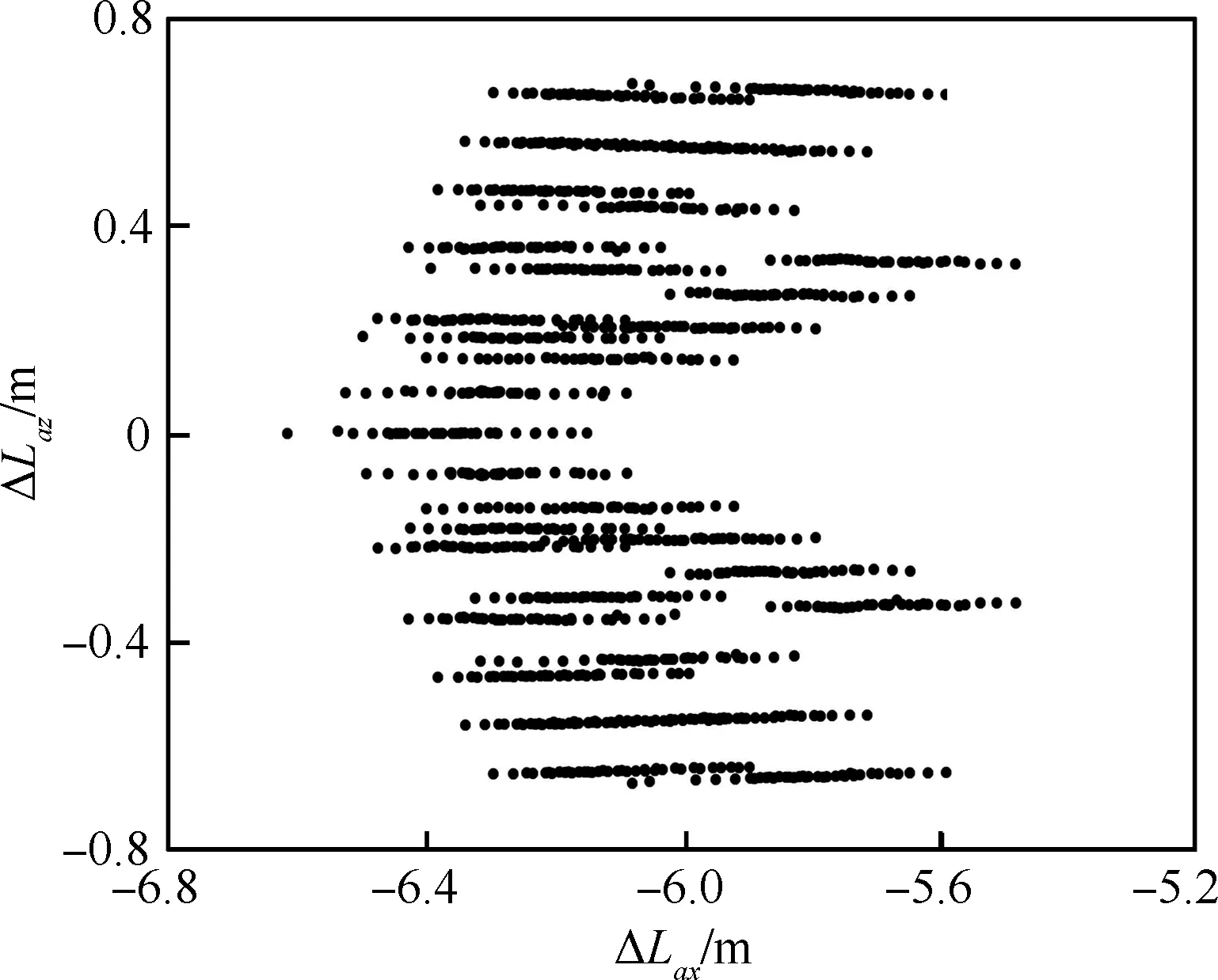
图18　底罩质心横移量结果图Fig.18　Map of lateral displacements of center of mass of tail cover

根据灵敏度分析结果找出风速、风向角、铰链摩擦系数等对分离过程影响较大的因素，进行正交试验，每个因素计算时分6个等级，得到的结果如图 18所示，其中黑色圆点为主发动机点火时质心横移位置。由于顺风时底罩落点更远，为了降低计算量，风向角设置在±90°范围内，也就是底罩运动处于逆风和侧风方向。为了分离安全，要求底罩x方向横移要大于4 m以躲开主发动机的喷气流，图中横移量均大于5.5 m，在安全范围内，说明分离方案在干扰下能够顺利进行。

底罩落点要求在发射车10 m半径圆以外，以防止砸伤相关设备和人员。底罩落点位置计算结果见图19，其中黑点为落点位置，落点位置受风速和风向角影响最大，由于每个因素划分为6个水平，并且风影响最大，导致落点成团分布，通过放大图可以看到每个落点团内的分布情况。

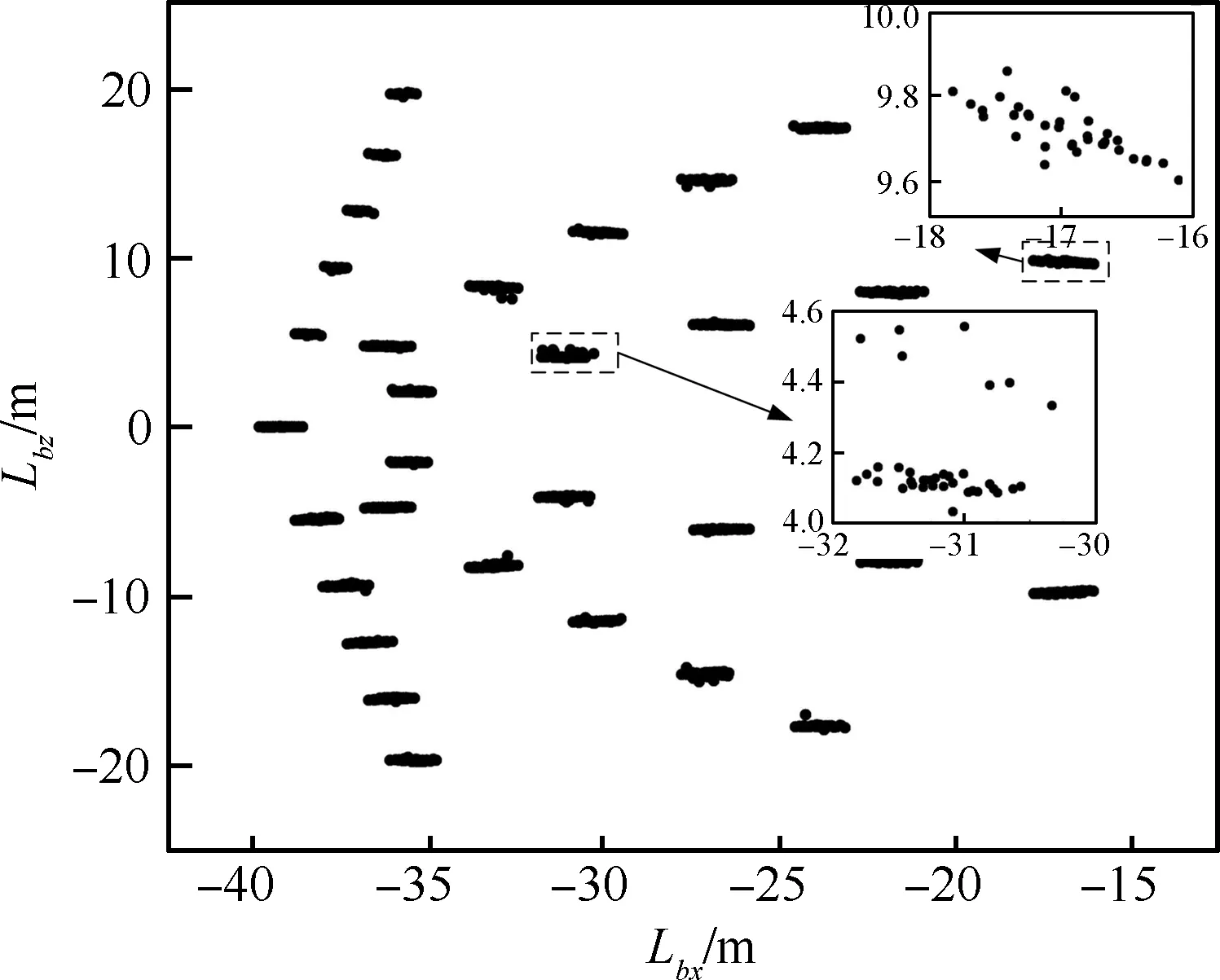
图19　底罩落点结果图Fig.19　Map of falling points of tail cover

底罩落点位置在逆风和侧风状态下x方向分布于-40～-15 m范围内，z方向落点位置在-20～20 m范围内，结果说明该分离方案能保证发射车和相关设备的安全。

5　结　论

1) 研究分析了底罩整体旋抛分离方案，该方案采用铰链机构改变尾罩运动方向，避开主发动机的喷气流，并且落地时避开地面的设备和人员。

2) 采用CFE法建立了底罩分离的动力学方程，对铰链摩擦力等多种分离力和干扰进行了建模分析，得到了分离角度、弹簧刚度系数和预紧力对分离过程的影响，并有针对性的进行了优化。本文对分离过程多种偏差进行了灵敏度分析，得到了对分离重要指标影响较大的因素。

3) 最后对分离方案中影响较大的偏差因素进行了正交仿真试验，得到了主火箭开机时刻底罩质心和底罩落地点的分布均在要求范围内，说明整体侧抛方案是可行的，能够满足底罩分离的各项要求。

4) 本文所采用的研究方法和计算方案可以协助设计人员确定分离体的落区，进行相关人员的保护和相关设备的防护工作。

[1]马溢清， 李欣. 潜射导弹水下垂直发射方式综述[J]. 战术导弹技术, 2010(3): 124-128.

MA Y Q, LI X. Review on underwater vertical-launching mode for submarine-launched missiles[J]. Tactical Missile Technology, 2010(3): 124-128 (in Chinese).

[2]侯世明. 导弹总体设计与试验[M]. 北京: 中国宇航出版社, 2009: 416.

HOU S M. Missile design and test[M]. Beijing: China Astronautic Publishing House, 2009: 416 (in Chinese).

[3]PAMADI B N, TARTABINI P V, TONIOLO M D, et al. Application of constraint force equation methodology for launch vehicle stage separation[J]. Journal of Spacecraft and Rockets, 2013, 50(1): 191-205.

[4]ROITHMAYR C M, HODGES D H. Forces associated with non-linear non-holonomic constraint equations[J]. International Journal of Non-Linear Mechanics, 2010, 45(4): 357-369.

[5]CICCI D A, QUALLS C, LANDINGHAM G. Two-body missile separation dynamics[J]. Applied Mathematics and Computation, 2008, 198(1): 44-58.

[6]HU X Z, CHEN X Q, ZHAO Y, et al. Optimization design of satellite separation systems based on multi-island genetic algorithm[J]. Advances in Space Research, 2014, 53(5): 870-876.

[7]PAMADI B N, NEIRYNCK T A, HOTCKO N J, et al. Simulation and analyses of stage separation of two-stage reusable launch vehicles[J]. Journal of Spacecraft and Rockets, 2007, 44(1): 66-80.

[8]JEYAKUMAR D, RAO B N. Dynamics of satellite separation system[J]. Journal of Sound and Vibration， 2006, 297(1): 444-455.

[9]张科南， 李鹏飞， 陈万春， 等. 某飞行器级间分离气动力/约束力/飞力综合建模与仿真[J]. 系统仿真学报, 2012, 24(10): 2227-2231.

ZHANG K N, LI P F, CHEN W C, et al. Modeling and simulation coupled aerodynamics, constraint force and flight dynamics for stage separation of aircraft[J]. Journal of System Simulation， 2012, 24(10): 2227-2231 (in Chinese).

[10]张科南， 陈万春. CFE方法在导弹发射动力学建模中的应用[J]. 北京航空航天大学学报, 2010, 36(12): 1404-1406.

ZHANG K N, CHEN W C. Application of constraint force equation method for missile launching dynamics modeling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(12): 1404-1406 (in Chinese).

[11]OH C, SUN B, PARK Y, et al. Payload fairing separation analysis using constraint force equation[C]//2010 International Conference on Control, Automation and Systems. Piscataway, NJ: IEEE, 2010: 1134-1138.

[12]TARTABINI P V, ROITHMAYR C M, TONIOLO M D, et al. Modeling multibody stage separation dynamics using constraint force equation methodology[J]. Journal of Spacecraft and Rockets, 2011, 48(4): 573-583.

[13]ROSHANIAN J, TALEBI M. Monte Carlo simulation of stage separation dynamics of a multistage launch vehicle[J]. Applied Mathematics and Mechanics, 2008, 29(11): 1411-1426.

[14]华楠， 阎君. 新型尾罩分离方案及分离过程的仿真[J]. 导弹与航天运载技术, 2005(2): 4-8.

HUA N, YAN J. A new trail cover separation concept and simulation of separation process[J]. Missiles and Space Vehicles, 2005(2): 4-8 (in Chinese).

[15]王恒， 由小川， 林崧， 等. 火箭尾罩导向段分离仿真分析[J]. 导弹与航天运载技术, 2011(5): 15-19.

WANG H, YOU X C, LIN S, et al. Numerical simulation of rocket aft dome separation[J]. Missiles and Space Vehicles, 2011(5): 15-19 (in Chinese).

[16]晁锐， 杨蓉， 赵新强， 等. 一种滞留式尾罩分离技术[J]. 导弹与航天运载技术, 2013(3): 12-14.

CHAO R, YANG R, ZHAO X Q, et al. An arrested trail cover separation technology[J]. Missiles and Space Vehicles, 2013(3): 12-14 (in Chinese).

[17]贾如岩， 王涛， 江振宇， 等. 导弹尾罩分离运动不确定性分析[J]. 国防科技大学学报， 2014, 36(6): 88-92.

JIA R Y, WANG T, JIANG Z Y, et al. Uncertainty analysis of the rocket trial cover separation[J]. Journal of National University of Defense Technology, 2014, 36(6): 88-92 (in Chinese).

[18]李慧通， 王旭刚， 赵阳. 考虑复杂因素的两体分离仿真软件设计[J]. 系统仿真学报, 2013, 25(12): 2851-2859.

LI H T, WANG X G, ZHAO Y. Design and development of simulation software for two-body separation calculation considering complicated factors[J]. Journal of System Simulation, 2013, 25(12): 2851-2859 (in Chinese).

[19]王汉平， 吴友生， 程栋， 等. 潜射模拟弹弹射后效分析[J]. 船舶力学, 2010, 14(10): 1122-1128.

WANG H P, WU Y S, CHENG D, et al. Analysis of ejection after-effect for underwater launched emulation missile[J]. Journal of Ship Mechanics, 2010, 14(10): 1122-1128 (in Chinese).

[20]胡仁海， 倪火才， 陈军峰. 燃气后效对发射体影响研究[J]. 导弹与航天运载技术, 2012(5): 11-14.

HU R H, NI H C, CHEN J F. Effect on projectile applied by aftereffect of exhaust gas[J]. Missiles and Space Vehicles, 2012(5): 11-14 (in Chinese).

[21]关士臣. 关于转动副摩擦问题的探讨[J]. 西安工业大学学报, 1986(4): 87-92.

GUAN S C. Discussion on the issue of rotation friction[J]. Journal of Xi’an Technological University, 1986(4): 87-92 (in Chinese).

[22]何竞飞， 聂荣光， 浮志强. 含转动副摩擦夹持机构精确力学建模[J]. 现代制造工程, 2008(11): 86-91.

HE J F, NIE R G, FU Z Q. The precise mechanical modeling of gripping machine including revolute joint friction[J]. Modern Manufacturing Engineering, 2008(11): 86-91 (in Chinese).

[23]王晓青， 王小军， 王国辉. 空射运载火箭多学科优化设计[J]. 导弹与航天运载技术, 2008(5): 1-5.

WANG X Q, WANG X J, WANG G H. Multidiscipline optimization design of air launched vehicle[J]. Missiles and Space Vehicles, 2008(5): 1-5 (in Chinese).

李慧通男， 博士研究生。主要研究方向： 飞行器仿真， 多体动力学。

Tel: 0451-86417756

E-mail: lihuitongyx@126.com

赵阳男， 博士， 教授， 博士生导师。主要研究方向： 飞行器仿真， 振动与冲击。

Tel: 0451-86417756

E-mail: yangzhao@hit.edu.cn

田浩男， 硕士， 副教授。主要研究方向： 飞行器仿真， 柔体动力学。

Tel: 0451-86402079

E-mail: dongda@hit.edu.cn

黄意新男， 博士研究生。主要研究方向： 航天器机构动力学， 线缆动力学。

Tel: 045-86417756

E-mail: huangyixinde@hit.edu.cn

Modeling and analysis of separation for missile tail cover

LI Huitong, ZHAO Yang*, TIAN Hao, HUANG Yixin

School of Astronautics, Harbin Institute of Technology, Harbin150001, China

Tail cover, which is used to protect the first stage engine during cold launch of missile, should be thrown after launch. In order to prevent the tail cover from hitting the ground equipment, the detailed separation scheme of lateral fling with connected hinge is adopted using spring as separation energy in the separation. The separation movements and dynamic characteristics are studied, and the kinematics and dynamics models of separation are built. The sensitivity analyses of multiple uncertain factors influencing tail cover are conducted such as aerodynamic force, spring force and negative air pressure during separation. Moreover, the impacts of separation angle of tail cover and the related coefficients of spring on separation process are obtained by simulating and optimizing the coefficients. Ultimately, centroid spreading range when the main engine gets started and landing point’s range of tail cover are achieved by the orthogonal test for separation scheme considering complex deviations.

hinge; dynamic modeling; separation; sensitivity analysis; simulation

2015-07-10； Revised： 2015-12-18； Accepted： 2016-02-26； Published online： 2016-03-0914:47

s： National Basic Research Program of China (2013CB733004); National Key Discipline Laboratory Open Foundation (HIT.KLOF.MST.201508)

. Tel.： 0451-86417756E-mail: yangzhao@hit.edu.cn

2015-07-10； 退修日期： 2015-12-18； 录用日期： 2016-02-26；

时间： 2016-03-0914:47

www.cnki.net/kcms/detail/11.1929.V.20160309.1447.004.html

国家“973”计划 (2013CB733004); 国防重点学科开放基金 (HIT.KLOF.MST.201508)

.Tel.： 0451-86417756E-mail: yangzhao@hit.edu.cn

10.7527/S1000-6893.2016.0052

V412.1

A

1000-6893(2016)06-1876-12

引用格式： 李慧通， 赵阳， 田浩， 等． 导弹抛底罩过程建模与分析[J]． 航空学报, 2016, 37(6): 1876-1887. LI H T, ZHAO Y, TIAN H, et al. Modeling and analysis of separation for missile tail cover[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1876-1887.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160309.1447.004.html