高中信息技术与数学算法教学整合的若干思考

黄求标（泰宁第一中学，福建泰宁354400）

高中信息技术与数学算法教学整合的若干思考

黄求标
（泰宁第一中学，福建泰宁354400）

高中数学算法教学普遍存在“纸上谈兵”的问题，应用计算机辅助软件制作程序框图十分简单，能编译为可执行文件运行，立即检验算法是否正确，非常适合高中师生讲解或研习算法使用。

算法教学；程序框图；程序代码；编译

在普通高中数学课程标准中，算法模块中要求学生通过模仿、操作、探索，学习设计程序框图表达解决问题的过程；体会算法的基本思想以及算法的重要性和有效性，发展有条理的思考与表达的能力，提高逻辑思维能力［1］。教育部《普通高中数学课程标准（实验）》在阐述高中数学课程的基本理念时，明确指出，当今知识经济时代，计算机技术与数学相融合，正在对数学课程内容的组织和呈现方式、数学教学的过程与方法产生深刻影响。教师应尽可能使用各种教育技术手段，加强数学教学与信息技术的融合，鼓励学生运用信息技术手段进行探索与发现学习。

一、算法教学存在的问题

算法作为具体的教学内容进入中学数学的教科书中，让一些数学教师觉得难以适应，算法教学该如何开展，学生如何学习算法，这些问题摆在了每一个高中教师的面前。信息技术作为一种现代教学手段如何更好的服务教学，提高教学效果。然而，放眼高中数学算法教学课堂，会发现存在诸多问题：

1.教师的算法水平和实现能力偏低，只会“纸上谈兵”

算法是高中数学新课改课程新增内容。许多一线高中数学教师，尤其是年龄较大的教师，求学期间没有系统学习过算法，在职培训也没有及时有效跟进，他们缺乏在计算机上验证程序的意识和能力，一般只能机械地讲讲程序框图，只会“纸上谈兵”式地模拟计算机执行程序框图，几乎从不安排学生集体上机实践，从而将本来实践性强、生动有趣的内容变成了机械呆板、枯燥乏味的说教。

2.“固化”“机械”的高考题型助长了教师的“纸上谈兵”

由于许多省市高考似乎就只考“根据程序框图写出程序运行结果”这种题型，而且往往只需照着框图模拟运行几趟（一般是3至6趟）就能直接得到结果，这种极端机械的题型，使得大部分一线数学教师和学生坚信只需“纸上谈兵”即可，从而大大削弱了算法教学。

3.算法教学存在两大“结构性”障碍，让师生止步于“纸上谈兵”

⑴分析问题时，得到了用自然语言表示的解题步骤，然后把它转化为程序框图，那么怎么实现这个“转化”？无论是在纸上还是在黑板或白板上画，无论用铅笔还是粉笔或白板笔或者用Word、Visio软件画程序框图，都费时费力！

⑵好不容易画出程序框图后，再怎么转化为程序？这个框图是给人看的，是人与人之间交流算法思想时用的，根本不能由计算机运行，只能用于纸上谈兵式的手工模拟！只有将它转换为程序，才能由计算机执行。由于学生先学程序框图，还不会写代码，因此无法写出代码验证算法。如果先学算法语句，学会编写程序代码，则又淡化了算法思想的主导作用，违背了算法教学的初衷：重在理解算法思想，不要上成程序设计课，这就是算法思想与程序实现之间的结构性矛盾：从逻辑上讲，先有算法思想，再编程实现；但从技术上讲，先要编写程序，运行程序才能实现算法检验算法——这样就陷入了类似于先有“鸡”还是先有“蛋”的“怪圈”。

离开算法的计算机实现，在纸上空谈算法是荒谬的。那么，如何激活机械呆板、死气沉沉的算法教学呢？归根到底，算法就是人们为了便于用计算机解决问题而创设的数学运算模型，由于上述诸多原因，倒在了离它被实现被实证的“最后一米”！传统数学课堂的“师-生”（或“师-演示电脑-生”）模式无法逾越这道“数字鸿沟”，必须引入“生-机（电脑）”模式，用信息技术破解本来就属于信息技术范畴的算法教学的困境，为算法思想的实现插上飞翔的翅膀。

算法最直观形象的表示方法就是流程图（即程序框图），因此，流程图就是高中算法教学的“牛鼻子”！无论用什么工具画流程图，画出来的图都是“死”图，这个图不能象真正的程序一样由计算机运行，是否正确只能在纸上模拟。一个能精确表示算法的流程图，却不能成为真正可运行的程序，从而使算法教学严重依附于程序设计，成为其附属物，甚至累赘！这导致两种后果：一是象数学上的算法课那样，算法的“实现”用纸上谈兵式的手工“模拟”代替（纯讲算法，忽视实现），二是像信息技术课程中的程序设计那样，把“鸡肋”似的算法直接忽略（讲了程序，算法就显得多余）！

二、信息技术在数学算法教学上的运用

学习算法，关键在于编写出让计算机执行的程序。看到计算机执行自己的程序并快速准确地给出问题的解答，会让学生体会到学习算法的成就感；另一方面，若执行程序未得到自己预期的答案，则可以对自己的算法和程序进行检查，

通过实践中的问题学习算法可以加深对算法及程序的认识和理解［2］。如果在算法课堂上，学生用拖拽图标的方式轻松地绘制流程图，系统自动生成程序代码，这样就使流程图成为可执行的“活”图，算法就成为可立即运行检验的“活”思想，那么学生在研究、设计算法时，就暂时不必理会程序语言代码和实现的细节，只需专注于算法思想，这样就大大降低了算法入门的门槛，算法就可以独立于程序设计，而成为程序设计的先导内容，真正成为程序的灵魂。显然，高中师生需要这样的工具平台，来辅助解决两个问题：一是快捷方便地绘制程序框图，二是自动编程实现算法验证算法。

算法是求解某一类问题所采用的一组定义明确、操作有序的步骤。通俗地说，就是计算机解题的过程。对算法进行描述，通常可以使用自然语言、程序框图、程序代码等方式。

例如，用计算机来计算圆的面积，即用自然语言描述算法［3］：

第1步：用户要把圆的半径r的值告诉计算机，即输入圆的半径r；

第2步：计算机用公式S=πr2计算圆的面积（圆周率也要明确告知计算机）；

第3步：计算机要把圆的面积S的值反馈给用户，即输出圆的面积S。

这种用自然语言描述的算法不直观，有时可能还有歧义，计算机也不明白人类的语言。于是，人们就想出了另外一种形式——用一种特定的图形把算法直观、准确地表达出来，这就是程序框图。启动软件，“流程图窗口”中会自动创建了一个“最简单”的程序框图：一个“开始”图标和一个“结束”图标，在这两个图标之间有一条“流程线”，如图1所示。用软件计算圆的面积操作如下。

第1步：输入圆的半径。点击“图标工具箱”，选择“输入”图标（平行四边形），按住鼠标左键拖拽到流程线上，至出现虚线框时释放左键，插入一个“输入”图标。输入字母r，表示圆的半径（为严谨起见，向图标内键入的内容在文章中一律加下划线表示，实际录入时则不必加下划线）。

图1 用画程软件绘制“计算圆的面积”程序框图

第2步：用公式计算圆的面积。点击“图标工具箱”，选择“处理”图标（矩形），拖拽一个“处理”图标到流程线上，在图标里面输入计算圆的面积的公式：S= 3.14159*r^2，变量S表示圆的面积，圆周率π直接给出常数3.14159，乘号用“*”号表示，r是半径，乘方符号“^”是主键盘数字6的上档键，按住Shift键不放，再按下6，这样就输入了乘方符号“^”。

第3步：输出圆的面积。点击“图标工具箱”，选择“输出”图标（平行四边形），拖拽到流程线上释放，在输出图标内键入变量S。

结果表明，这个程序框图所对应的程序代码是正确的，从而也表明程序框图是正确的。

再来分析一下复杂的数学问题——考拉兹猜想。

（一）算法设计

德国数学家考拉兹（Lothar Collatz）于1930年代提出考拉兹猜想，又名3n+1猜想或冰雹猜想，是指对于每一个正整数，如果它是奇数，则对它乘3再加1；如果它是偶数，则对它除以2，如此循环，最终都能得到1。设计算法验证考拉兹猜想（当然只能是在有限的数据范围内验证），还是先用自然语言来描述算法：

第1步输入n（正整数）；

第2步若n为偶数，则将其除以2，否则（n为奇数），将其乘以3后加上1，结果仍用n表示；

第3步如果n=1，退出到第4步，否则转回到第2步；

第4步输出“考拉兹猜想成立！”

此时，用《画程》软件绘制流程图：

第1步，拖入一个输入图标，在其内键入n；

第2步，拖入一个判断-分支图标，条件怎么写？“n是偶数”，如何用计算机的语言表达呢？n除以2所得余数为0。在VB［4］或QBX7.1中用mod表示取余运算，如5 mod 3表示5除以3所得余数（为2），所以键入条件n mod 2=0，在“是分支”里拖入一个“处理”图标，在“处理”图标里键入赋值语句n=n2。在“否分支”里拖入一个“处理”图标，键入赋值语句n=n*3+1（如图2）。

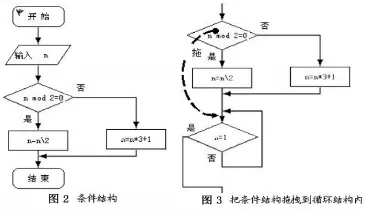
第3步，这里有一个词非常关键：“转回”！也就是说，流程线要回到上面来！要用“判断-循环”图标，拖入一个“判断-循环”图标，条件怎么写呢？键入n=1，“如果n=1则退出”，所以这个“否”与“是”要交换，只要双击“是”或“否”就改变了（如图3）。“否则，转回第2步”，要转到上面来，怎么操作呢？流程线不能拖动，可以把上面的条件结构拖拽到循环返回线的下面来（如图3），这样就实现了“转回第2步”。

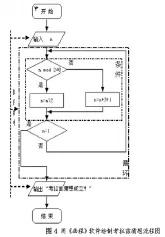
第4步，拖入一个输出图标，键入“考拉兹猜想成立！”（如图4）

（二）三种基本结构

人们已经证明：任何复杂的程序结构，都可以用三种基本结构（顺序结构、条件结构、循环结构）或它们的组合来表示。

本例的总体结构是：①输入n；②验算考拉兹猜想；③输出结论。它们构成了顺序结构，其中“验算考拉兹猜想”就是循环结构（由判断-循环图标“n=1”主导），而“n是否偶数”组成的条件结构，嵌套于上述的循环结构的循环体内，这样，本例同时包含了三种基本结构。

（三）单步运行

保存刚才所画流程图，编译、运行程序（注意n为正整数，且任何时候n不超出2147483647）。这个程序很快就输出“考拉兹猜想成立！”由于其中间运行过程看不到，是不是有点不放心？选择“单步运行”功能，可以一步一步地运行程序，用户可以“看清”每步运行的结果。单击“单步运行”工具，弹出一个提示框，单击“确定”按钮，弹出“单步运行”窗体，单击“开始”（或“下一步”）按钮将开始单步运行（若勾选“自动”复选框，则自动单步运行（如图5）。

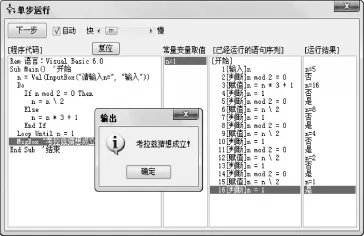
图5“单步运行”窗体展示程序每一步运行的状况

信息技术与高中数学算法教学整合能帮助学生从枯燥、深奥的算法理论上升到理解、消化知识的高度。信息技术为学生提供直观、易操作让学生所见所得的算法内函展示，使深奥的数学算法理论通过手、眼、脑等多种器官的刺激深深扎根于学生的知识体系中。

［1］数学课程标准研制组.普通高中数学课程标准（实验稿）［S］.北京：北京师范大学出版社，2000.

［2］张景中.超级画板自由行［M］.北京：科学出版社，2006.

［3］伍先军.流程图（程序框图）高考题型例解［J］.中学数学，2012（3）.

［4］张福祥.VB程序设计基础工业［M］.北京：中国电力出版社，2003.

（责任编辑：邹开煌）