一种遗传算法实现的图聚类匿名隐私保护方法
姜火文 曾国荪 胡克坤
1(同济大学计算机科学与技术系 上海 200092)2(江西科技师范大学数学与计算机科学学院 南昌 330038)3(嵌入式系统与服务计算教育部重点实验室(同济大学) 上海 200092) (hwjiang@tongji.edu.cn)
一种遗传算法实现的图聚类匿名隐私保护方法
姜火文1,2,3曾国荪1,3胡克坤1,3
1(同济大学计算机科学与技术系 上海 200092)2(江西科技师范大学数学与计算机科学学院 南昌 330038)3(嵌入式系统与服务计算教育部重点实验室(同济大学) 上海 200092) (hwjiang@tongji.edu.cn)
聚类匿名是一种典型的社交网数据发布隐私保护方案,其基础工作是图聚类.图聚类为一类NP难的组合优化问题,便于使用搜索优化算法.现有图聚类匿名方法缺少此类启发式搜索算法.为此,研究一种利用遗传算法实现的图聚类匿名方法,利用贪心法进行结点聚类预划分,以构造初始种群;依据关系拟合理论建立个体适应度函数;根据个体编码特点,分别提出一种多点错位的交叉算子和基因位交换的变异算子.图聚类模型综合考虑了结点的结构和属性信息,而遗传算法的全局化搜索优化能力保障了图聚类质量,因此,该方法具有较强的隐私保护性.实验表明了该方法在提高聚类质量和减小信息损失方面的有效性.
社交网络;图聚类;隐私保护;k-匿名;遗传算法
随着网络社交平台的迅猛发展,社交网络里积累下海量个人及其社会关系信息,构成一类具有重大潜在价值的图大数据.同时,这些图数据也蕴含了大量用户不愿意被公众获知的隐私.近年来,在维持社交网络数据可用性的同时如何保护个人隐私,成为一个严峻的问题[1].社交网络中隐私信息类型广泛,例如用户的难言性“疾患”、不愿披露的“薪酬”等属性值,用户间联系频度(一般意味着某种亲密关系或伙伴关系)等.面对恶意的隐私盗取,那种仅将用户身份信息隐去的简单匿名方法并不能防止隐私泄露.因为网络图上结点和边的属性及拓扑结构等信息都可能被用于识别用户身份[2].例如某结点的度或d-邻域结构可能导致该结点被唯一或高概率地识别出来[3-4].另外,在属性-社交网络场景中,用户即使未标记某隐私属性,但也可能被推测出较大概率地具有该隐私属性[5].例如,虽然某用户没有公开其宗教信仰,但根据其绝大多数朋友都喜欢听佛教音乐,可以较大概率地推测其信奉佛教[6].剑桥大学一项研究也表明,Facebook上“likes”某些事物将会暴露用户的智商、性取向、宗教信仰等重要信息[7].
k-匿名是一种已广泛应用于关系表数据发布的隐私保护机制,目前也多被运用到社交网络数据发布隐私保护,结点k-匿名即为一种应用机制.结点k-匿名的思想是将网络图中所有结点聚类成一些超点,每个超点至少包含k个结点,超点中结点相互之间不可区分,因此在该社交网络中,受结点再识别攻击而导致隐私泄露的概率小于1k[6].可见,结点k-匿名的实质是图聚类匿名.如图1所示,设图1(a)为社交网络模型图,图1(b)即为图1(a)的结点2-匿名图.图聚类匿名的一个关键问题是图聚类方法的选择,因为聚类方法决定聚类结果,影响匿名效果.理论上求最佳聚类结果实质是一类NP难的组合优化问题,一般使用启发式搜索算法更容易找到优质解.
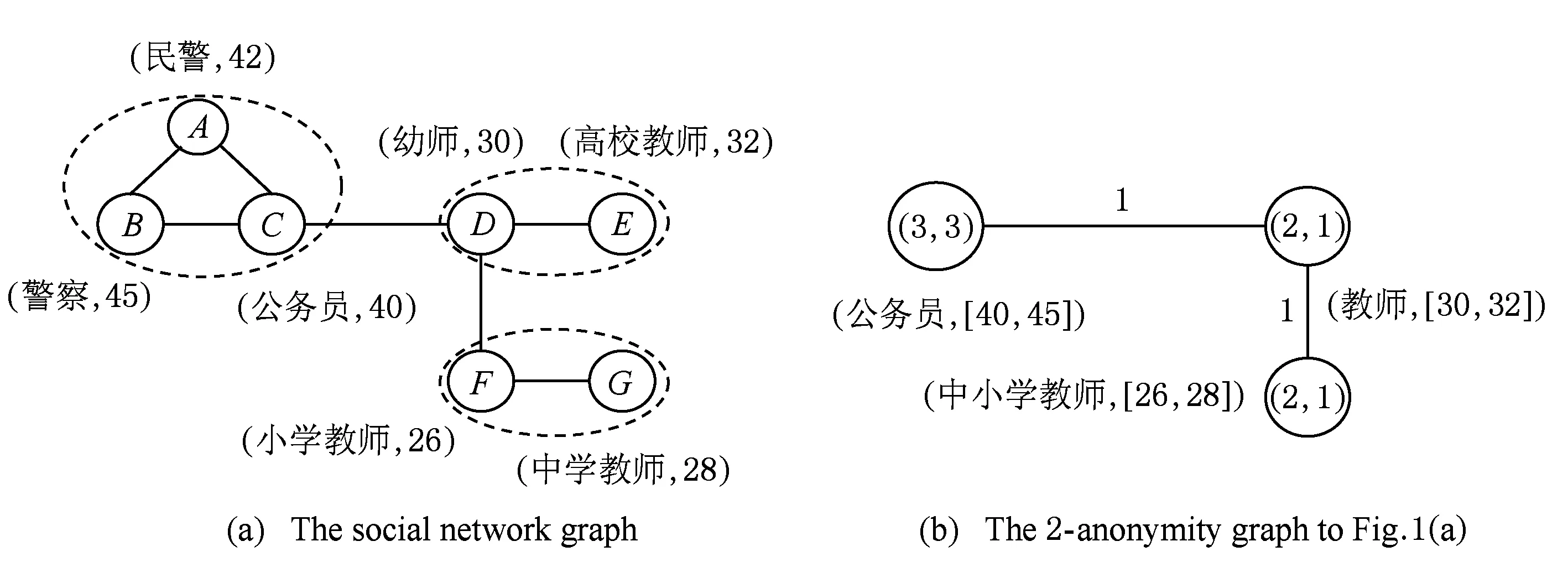
Fig. 1 The social network graph and its anonymity graph.图1 社交网络模型图及其匿名图
现有图聚类匿名方法中常见贪心聚类方法、有序聚类方法等,缺少智能搜索算法.为此,本文研究用遗传算法实现网络图聚类匿名保护,综合结构和属性的相似性,对结点进行聚类划分后匿名发布.本文的主要贡献为:
1) 引入遗传算法进行图聚类匿名隐私保护;
2) 量化结点间结构和属性的相似性,提出基于属性加权图聚类的种群初始化算法;
3) 根据机器学习中的关系拟合理论,提出个体适应度求值算法;
4) 根据个体编码特点,提出一种多点错位的交叉算法和交换基因位的变异算子.
1 相关工作
目前,k-匿名机制在社交网络数据隐私保护中占有重要地位.根据采用匿名方法的不同,k-匿名方案基本分为基于结构变换和基于超级结点的两大类[8].基于结构的变换常见基于结点的度数或邻居图等结构特征,构造k-度匿名或k-子图匿名,其采用的手段主要是边、结点的增、删修改.例如:为防范根据结点度的识别攻击,Liu等人[1]分别设计了基于分治法和最大邻差的2种度序列划分算法,并籍以构建了k-度匿名图;为抵御基于子图结构的攻击,Zou等人[9]提出一种匿名化算法,使匿名图中总能找到k个不同的同构子图;同样为抵御基于结点1-邻域子图的识别攻击, Zhou等人[3]借鉴关系数据隐私保护的(k,l)匿名模型,提出一种适用于社交网络数据,满足k-匿名和l多样性的匿名方法,并证明其为NP难问题;为保证边的匿名性,Cheng等人[10]提出一种k-同构匿名化算法,能够防止对边存在性的合理推测;为防止可能根据结构信息或共享敏感属性的双重攻击,Yuan等人[4]通过在原图中添加噪音结点的方法,构造了一种k-度-l-多样性匿名模型.基于超级结点的变换实际就是结点k-匿名方案,最早由Zheleva等人[11]提出这一模型.其后,针对不同的防范背景或性能要求等情形,研究者对这一模型进行了不同的修改完善,提出了多种结点聚类匿名方法.Campan等人[12]首次提出一种结点聚类匿名的贪心算法SaNGreeA,可以同时保护结点非标识属性和连接关系,同时针对匿名过程产生的结构信息损失给出了一种定量计算方法;Wang等人[13]提出一种贪心聚类算法MASN,对SaNGreeA算法进行了改进,使其具备保护敏感属性的功能,可以抵御同质化攻击;SaNGreeA[12]算法和MASN[13]算法都是对无权图的聚类匿名,针对带权图的匿名保护, Skarkala等人[14]提出一种与SaNGreeA近似的方法,设置超边权重为原连接边的平均权重,将超边间包含的具体边权重隐藏起来,起到保护作用,其中超点结构能将用户身份泄露概率降至1k以内.另外Tassa等人[15]提出基于有序聚类的匿名方法,可以实现集中式网络环境下的数据隐私保护,同时首次针对结点间不完全可见的分布式图数据的隐私保护,设计了有序聚类匿名算法;Yang等人[16]则提出一种基于安全协议的EM算法,针对非连接结点间互不可见的图数据实现了结点聚类.
2 问题模型与定义
社交网络表现为特定群体中多个个体及他们间相互联系组成的集合,最适合用图来表示.其中,结点表示个体;边表示个体间的联系;个体的特征信息,如职业、年龄、学历等是刻画个体的重要数据,统称为结点属性,通常以一个属性值向量表示.常见的社交网络结构模型为简单的图模型G(V,E),这只是考虑了用户结点及其连接关系,并没有考虑结点属性信息.为全面刻画社交网络数据,我们定义社交网络图如下:
定义1. 社交网络图. 对包含了用户属性数据和用户间社交关系数据的社交网络,用图模型描述,形式化表示为一个三元组,即G=(V,E,A),称这个图G为社交网络图.
在图G中,V={v1,v2,…,vn}为图中结点集;E={(vi,vj)|1≤i,j≤n,i≠j}为边集;A={a1,a2,…,as}为结点的属性集.图中任何边(vi,vj)表示结点之间的联系,为结构边.根据实际网络中实体间联系的紧密程度不同,结构边可以赋予不同的权值.本文假定各结构边具有相等的权值,均为1,则图连接的拓扑结构可以表示为邻接矩阵形式:
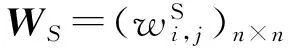

图中所有n个结点的属性值可用矩阵Attr=(αit)n×s表示,其中∀i∈{1,2,…,n},有αit∈at,t∈{1,2,…s}.属性at可能为数值型或类别型,例如,型如(职业,年龄)的二维属性集,“职业”属性为类别型,其属性值为离散型文本;“年龄”属性为数值型,其属性值为实数.属性类型差异不便于统一度量其相似度,为此分开度量.∀αit,αjt∈Attr,定义其属性相似度计算为
Asim(αit,αjt)=
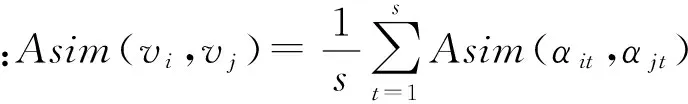
定义2. 属性加权图. 对图G中任意2个结点vi和vj,如果Asim(vi,vj)≠0 ,认为在vi和vj间存在一条权值为Asim(vi,vj)的属性边,并将其和结构边合并,合并后的边权值取为原两者权值和.由此得到的带权图,称为属性加权图,记为GSA.
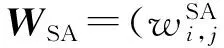
定义3. 图聚类. 根据结点间的某种相近或相似性,利用聚类方法将社交网络图的所有结点划分成一些聚类(簇),这个过程成为图聚类.
图聚类可以表示为社交网络图G上的一种映射关系φ:(v1,v2,…,vn)→(V1,V2,…,Vm),φ满足2个条件:
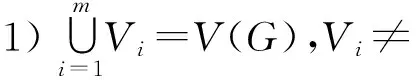
2) 1≤∀i,j≤m,i≠j,Vi∩Vj=∅.
定义4.k-聚类匿名图. 对社交网络图G进行图聚类,使每个簇内结点数不小于k.隐匿各簇内所有结点的连接结构和属性值,每一簇构成的子图用一个超点取代.子图内各结点的属性值被统一概化成一个超点的属性值;超点上标明所隐含的用户结点个数和内部边的条数;任意2个簇间,若原来共有t条边相连,则只用一条带权值t的超边取代;若原来没有任何边相连,则没有超边相连.由此得到由m个超点构成的“浓缩”了的图,称为k-聚类匿名图.
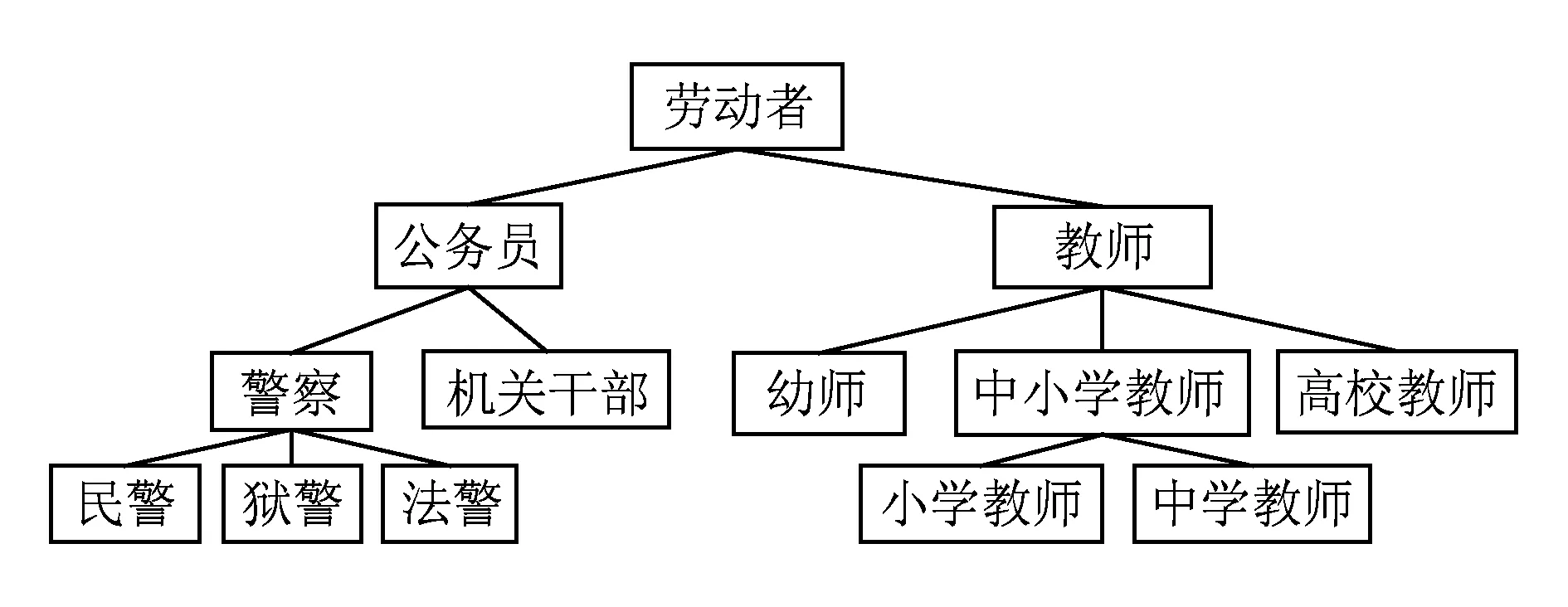
Fig. 2 The generalization hierarchy tree of “occupation” attribute.图2 “职业”属性的概化层次树
图1(b)即为图1(a)聚类匿名后得到的一个2-聚类匿名图.聚类匿名过程需要对各超点作属性概化处理,将超点内所有结点的属性值概化成一个属性值.属性类型不同其概化方法也不一样,类别型属性的属性概化需要根据概化层次树进行,为此需要预先为每一个类别型属性建立概化层次树,例如图2即为一棵概化层次树.树中叶子结点为各个用户结点的属性值,各分支结点即为以其为根结点的子树中各叶子结点的概化值,根结点表示图中所有结点在该属性上的概化值.记超点Vt中各结点在属性ai上的取值集合为ai(Vt),属性概化方法为:如果ai是数值型,则其概化值为[minai(Vt),maxai(Vt)],如果ai是类别型,则其概化值取为ai(Vt)上所有叶子结点的最小上界结点.
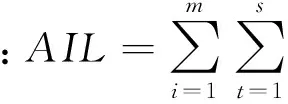
ail(Vi,t)=

图G的若干相似结点聚类为一超点,对外只发布超点的某些统计特性,表现为一个结点和属性值,隐藏了超点内的连接结构和各用户结点的属性信息,这体现为泛化技术的思想,能够防范常见的结构化攻击.可见,k-聚类匿名过程融合了隐私保护技术中的泛化技术和k-匿名技术,能够有效防范基于图结构或结点属性等背景知识的隐私推理攻击,将其攻击成功率至少降至1k以内,因而具有很强的隐私保护效果.对于大型社交网络,其k-聚类匿名只是在全局范围内作了一些微观“浓缩”,只要k不很大(一般取3~5即可保证隐私强度),原社交网络图的宏观结构与特性及蕴含的主要信息得以基本保持,故匿名后的图数据仍然具有较高的可用性.
3 图K-聚类匿名化遗传算法
遗传算法是一种模拟自然界生物进化过程的随机化搜索算法,特别适用于处理需要在复杂而庞大的搜索空间中寻找最优解的问题.图聚类匿名保护方法主要工作基础是图聚类,为一类典型的NP难问题,适合用遗传算法搜索最优解.本文研究利用遗传算法对图G进行k-聚类匿名化操作,以达到图数据隐私保护目的,方法的主要特点体现在种群初始化、适应度函数和交叉算子等3个计算部分.本节按算法流程先分节阐述各主要步骤,然后给出算法的整体描述.以下均假定图结点个数为n、每个结点包含s个属性、聚类个数为m、种群规模为q.
3.1 个体编码
种群中的每个个体都对应问题的一个解,假定对图中n个结点编号,问题的解适合用一个n维整数向量P=(p1,p2,…,pn)表示.这里,P中的任意一个pi表示结点vi所在的簇号,即:∀i∈{1,2,…,n},pi∈{1,2,…,m}.显然,∀i,j∈{1,2,…,n},i≠j,pi=pj表示结点vi和vj聚类在同一簇内.为此,我们采用这个十进制n维整数向量P作为个体编码,也称为染色体.例如,对7个结点的图,个体编码(1,2,1,3,2,1,3)表示聚类结果为{V1={v1,v3,v6},V2={v2,v5},V3={v4,v7}}.为表述方便,规定pi也记为P(i),如种群中某个染色体Px的第i个基因值,记为Px(i).
3.2 种群初始化
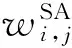
算法1. 个体初始化算法Initchrom(WSA).
输入:属性加权图邻接矩阵WSA;
输出:染色体P.
① P=(0,0,…,0);
②clus=1;*clus表示聚类编号*
③nodes=n;*nodes表示未划分的结点数*
④ ∀i∈{1,2,…,n},P(i)=clus,C={i};
⑤ Whilenodes≥2kdo*逐个划分聚类*
⑥ While |C| ⑦maxsum=0; ⑧ Fori=1 tondo*选取结点添加* then 3.3 个体适应度 适应度用于评价个体的优劣,直接影响下一代种群的产生,从而引导种群进化方向,在遗传算法中起到举足轻重的重要.给定任意一个染色体Px,Px对应图结点集V上的一种聚类划分结果,而集合V上的任意一种划分结果可以确定V上元素间的一个等价关系.设Px确定的等价关系为Rx,显然,Px对应的划分结果就是商集VRx;∀vi,vj∈V,若〈vi,vj〉∈Rx,则等价类[vi]Rx=[vj]Rx,即vi和vj在同一簇中.抽象层面看,图聚类是一个对图结点集合划分成多个簇的过程,划分的依据就是相似性,这种相似性可以被看成定义在图结点集上的一个二元关系,称为相似关系,不妨记为S.如属性加权图邻接矩阵WSA即定量反映其一种相似程度,设定一个阈值l,规定:若vi和vj的相似度大于l,即>l时,vi和vj的相似关系成立,即序偶〈vi,vj〉∈S.根据WSA的定义特点,不难理解,这个相似关系是自反的、对称的,但并非可传递的. 从机器学习角度理解,聚类是一种无监督的学习过程,S代表学习前的先验知识,Rx是学习后的后验知识.根据机器学习理论,好的聚类结果应该是最高程度拟合S的那个Rx.为此,我们定义|Rx∩S||Rx|为适应度函数,其中,Rx∩S表示关系Rx和S的交集,|Rx|表示Rx中的序偶个数.显然|Rx∩S||Rx|∈[0,1],|Rx∩S||Rx|越大,Px越好.下面给出|Rx∩S||Rx|的求解算法. 算法2. 染色体Px的适应度求解算法Fitval(WSA,l,Px). 输入:矩阵WSA、阈值l、染色体Px; 输出:适应度函数值. ①rs=0,r=0;*初始化* ② For eachc[i] do*初始化* ③c[i]=0; ④ End For ⑤ Fori=1 tondo ⑥c[Px(i)]=c[Px(i)]+1; ⑦ Forj=1 tondo*计算|Rx∩S|* ⑨rs=rs+1; ⑩ End If 算法2的计算量主要在于计算|Rx∩S|,其计算过程是一个双层循环,内层循环次数和外层循环次数均为结点个数n,故算法2的时间复杂度为O(n2). 3.4 遗传算子 3.4.1 选择 选择算子直接把优良的个体遗传到下一代,是对种群的优胜劣汰操作.选择算子需要在评估各个个体适应度的基础上进行,为此,对种群的每一个染色体Pi,先计算其适应度函数值Fitval(WSA,l,Pi).本文采用经典的赌轮选择法进行选择操作,方法是: 1) 根据式: g(i)=Fitval(WSA,l,Pi) 计算每个染色体Pi的选择概率g(i); 3) 在[0,1]区间内产生一个均匀分布的随机数rand,若rand≤prob1,则染色体P1被选中;若probi-1 以上步骤3重复执行q遍,即重新构成规模为q的种群. 3.4.2 交叉 由3.1节可知,染色体编码值只是簇的一个相对编号,不同染色体间的编码值并无必然关联,没有可比性.即同一染色体中的相同编码值可表示对应的结点在同一簇中,但不同染色体间的相同编码值可能表示不同簇.故这里交叉操作不能简单地采用2个染色体间对应基因位的一点或多点交叉,因为交叉后2个染色体间相同的编码号会产生混淆,也几乎必定会导致簇的大小不合规定. 针对本文染色体编码特点,我们提出一种多点错位交叉法:设2个交叉染色体为Px和Py,首先,分别从1到n位扫描两者的所有编码,如果聚类数m为奇数,将所有值为偶数的不同编码值按出现顺序排列,得到分别对应Px和Py的2个整数序列A=(a1,a2,…,at)和B=(b1,b2,…,bt),这里t=(m-1)2,A或B中的各整数都为互不相同的偶数;如果m为偶数,则将所有值为奇数的不同编码值按出现顺序排列,得到的整数序列A或B中都为互不相同的奇数值,且t=m2.然后,对Px和Py中从1到n位中的所有偶数值编码(如果m为奇数)或奇数值编码(若m为偶数),分别用B和A逐遍取代.下面给出该交叉算法. 算法3. 染色体交叉算法Crossover(Px,Py). 输入:2个待交叉操作的染色体Px和Py; 输出:交叉算子后的2个染色体Px和Py. ①m=nk;*初始化,m取整除后的整数商* ② A=(0,0,…,0); B=(0,0,…,0); e=0; f=0;*初始化* ③ Ifodd(m) then*m为奇数时偶数编码值交叉* ④ Fori=1 tondo*Px(Py)中相异偶数编 ⑤ If (Px(i)为偶数且不在A中) then ⑥ Px(i)放入A中;*Px中相异偶数编 ⑦ End If ⑧ If (Py(i)为偶数且不在B中) then ⑨ Py(i)放入B中;*Py中相异偶数 ⑩ End If Px(Py) 中偶数编码值* 取代Px中偶数编码值* 取代Py中偶数编码值* 类上; 算法3的计算量主要在将Px(和Py)中所有不同的偶数编码值放入A(和B)中,通过一个执行次数为n的for循环语句完成.循环体主要是判断某个Px(i)是否在A中和Py(i)是否在B中,其执行次数分别等于变化中的A和B的元素个数,其上限为m2,故算法3的时间复杂度为O(n×m).交叉算子是产生新个体的主要方法,藉由交叉算子,遗传算法的全局搜索能力得以巨大提高. 3.4.3 变异 变异操作一般是根据变异概率对染色体的某些基因值作变动,以形成一个新的个体.根据本文染色体编码特点,变异操作并不能简单地选定某些基因位作编码值改变,因为可能导致相关簇的元素个数小于k.为按变异概率(取1‰)改变个体某些基因值,又不产生错误染色体,本文提出变异算子是:从种群中任选半数(q2个)染色体,对选出的每个染色体的所有基因位,每隔1 000位(包括最后不足1 000个的基因位)选取首尾2个基因位,交换其编码值.如当n=1600时,对染色体Px,分别是Px(1)和Px(1000)交换数值、Px(1001)和Px(1600)交换数值.可以计算出变异基因位的数目为:(q2)×(n1000×2),因为q2和n1000都只能取整数值,我们取不小于其相应实数值的最小整数,故变异概率(变异基因位数总基因位数)等于或略大于1‰.变异算子是产生新个体的辅助方法,它决定了遗传算法的局部搜索能力.交叉和变异相互配合,共同完成对解空间的全局和局部搜索. 3.5 图聚类匿名隐私保护的遗传算法 遗传算法的主体包括染色体编码、种群初始化、适应度求值和遗传算子4个重要部分.基于上述3.1~3.4节的内容,本节提出一种图聚类匿名隐私保护的遗传算法(genetic algorithm for clustering-anonymity graph privacy preservation, GA-CAG).算法步骤是:1)初始化种群;2)计算各染色体的适应度;3)判断当2次迭代平均适应度值小于某个阈值λ(取0.0001)或迭代次数t大于预设值T(取200)时结束迭代,否则继续遗传迭代;4)依次执行选择-交叉-变异这3个遗传算子后返回步骤2);5)根据适应度值最大的染色体进行聚类匿名后输出结果,算法结束.GA-CAG算法描述如下: 算法4. 图聚类匿名隐私保护的遗传算法GA-CAG(G). 输入: 社交网络图G; 输出:k-聚类匿名图G′. ①t=0;*t为当前迭代次数* ②FS=0;*FS为各个体适应度和* ③dif=0;*dif为相邻两代FS值差* ④ 按θ=0.5求出属性加权图邻接矩阵WSA; ⑤ Fori=1 toqdo*初始化种群* ⑥Initchrom(WSA); ⑦ End For ⑧ Fori=1 toqdo*求个体的适应度和* ⑨FS=FS+Fitval(WSA,l,Pi); ⑩ End For 上述算法4描述表明,GA-CAG算法的主要工作在迭代搜索最优图聚类结果,而完成每次迭代的主要计算量在于求各个体适应度和执行“选择-交叉-变异”遗传算子.根据3.3节论述,算法2求各适应度的时间复杂度为O(n2);根据3.4节的论述,3种遗传算子的主要工作在于算法3的交叉算子,其时间复杂度为O(n×m).故GA-CAG算法的时间复杂度大致为T×(O(n2)+O(n×m)),由于T为预设的迭代次数常量(本文取为50),可以认为GA-CAG算法的时间复杂度仍然为O(n2). 本节通过实验分析本文所提GA-CAG算法的性能,实验过程与功能相似的SaNGreeA[12]算法和MASN[13]算法进行比较,考虑可比性更好,对其中的参数α,β和l均分别设定为0.5,0.5和2.实验数据来自UC Irvine Machine Learning Repository[12]①http://www.ics.uci.edu/~mlearn/MLRepository.html的Adult数据集,分别从中任意取500个结点和800个结点构成的社交网络,记为DS1和DS2,各组实验均分别在这2组数据集上进行.实验环境为:Intel®CoreTMi5-4210U CPU @ 1.70 GHz(2394 MHz);4.00 GB(1600 MHz)内存;希捷ST ST500LM000-SSHD-8 GB(500 GB)主硬盘;Microsoft Windows 8.1中文版 (64 b)操作系统;算法均采用Microsoft Visual C++ 7.0实现.由于算法的每次执行结果可能会略有不同,每组实验重复进行5次,结果取其平均值. 4.1 聚类质量分析 GA-CAG算法的关键工作是图聚类,为此,本节引入聚类密度和聚类熵2个评价指标[17],各自通过1组实验,以对比分析算法的聚类质量.聚类密度和聚类熵可以分别反映结构上和属性上的聚类效果[17].本节2组实验均在DS1和DS2数据集上进行.第1组实验是聚类密度的对比分析,定义聚类密度为 图3(a)和图3(b)分别给出了在两者数据集上3种算法的聚类密度对比及其随k值变化的规律.从图3可见:在两者数据集上,3种算法的聚类密度值都比较接近,总体上GA-CAG算法的density值略高.相比图3(a),在图3(b)上density值落差略大,反映出在结构上的聚类效果,当数据量不大时,3种算法非常相近,当数据规模变大,差别也有所变大,但总体差距不大.图3(a)(b)均显示随k值增大,聚类密度趋大变化,这是因为k值变大则聚类数目减少,聚类之间的联系将减少,即各超边所隐匿的外部边总数减少,相应地所有簇中的内部边总数增加,因而聚类密度变大. Fig. 3 The comparison of cluster density in datasets of DS1 and DS2.图3 在DS1和DS2数据集上的聚类密度比较 第2组实验是聚类熵的对比分析,聚类熵定义为 Fig. 4 The comparison of cluster entropy in datasets of DS1 and DS2.图4 在DS1和DS2数据集上的聚类熵比较 Fig. 5 The comparison of the information loss of attribute in datasets of DS1 and DS2.图5 在DS1和DS2数据集上的属性信息损失比较 4.2 信息损失分析 匿名带来的数据信息损失可以大致反映匿名后的数据可用性,一般信息损失越大意味着数据可用性越差.本节我们通过2组实验分别比较分析算法的属性信息损失和结构信息损失.各算法执行过程中,属性信息损失值AIL和结构信息损失值NSIL均按第2节所讨论到的计算方法求得,各类别属性的概化层次树均参照文献[12]给出. 图5给出了属性信息损失值AIL随k值变化的实验结果,从图5中可见,随着k值的变大,属性信息损失呈增大趋势.究其原因是:k值变大则每个聚类中的结点个数增多,各超点内部可能有更多的相异属性值被概化成同一个属性值,这个概化属性值对数值属性而言可能将有更广的域值范围,对类别属性而言可能将有更高的概化层次,故每个原结点的概化程度都可能变大,导致AIL值变大.图5还显示GA-CAG与MASN分别有最小和最大的AIL值,但总体差别不显著,说明GA-CAG通过遗传算法强大的搜索功能找到了更优解,而MASN在SaNGreeA的基础上通过l值使各聚类中的结点避免出现单一属性值,导致结点的概化程度可能增大,故其AIL值又比SaNGreeA算法略大.对比图5(a)和图5(b)可见,后者的属性信息损失略微增大.这个结果可以从2个方面得到解释,首先,因为AIL主要与属性个数和体现隐私保护强度的k值有关,而DS1与DS2上的属性个数相等,故两者在同等k值上的AIL值接近;其次由于后者数据规模大时,平均每个聚类中可能有更大比例的不同属性值被隐匿,以致AIL略有增大. 图6给出了结构信息损失值NSIL随k值变化的实验结果,可以发现,NSIL值随k值增大而增大,这是因为:k值增大则各超点构成的子图规模将变大,子图隐匿时将明显造成更多的边被隐藏,故导致NSIL值增大明显.另一方面,宏观上说,各聚类的规模增大而聚类数减少,意味着图结点划分更粗糙,整体图结构的局部“浓缩”程度更为显著,自然对整个图结构的损失更大.图6也可见,GA-CAG有相对最小的NSIL值,这也反映本文遗传算法能搜索到较好解;而SaNGreeA和MASN的NSIL值基本没有差别,这是因为这2种算法本身在功能上的差别对边的隐藏数目没有实质影响,即相等k值下两者匿名所造成的隐匿边的数目理论上没有差别,具有一定的随机性.比较图6(a)和图6(b)的结果,发现两者基本没有差别,考虑到聚类结果具有微小范围内的随机差异性,可以说明结点个数对整体图结构的平均信息损失没有影响. Fig. 6 The comparison of the structural information loss in datasets DS1 and DS2.图6 在DS1和DS2数据集上的结构信息损失比较 针对社交网络图数据的聚类匿名发布,考虑利用启发式优化算法搜索最优解,本文提出一种图聚类匿名遗传算法.按照遗传算法的流程框架,在依次描述了种群初始化算法、个体适应度值求解算法、赌轮法选择算子、多点错位的交叉算法和交换基因位的变异算子后,完整地给出了该GA-CAG算法.最后,多组实验验证了算法性能的优越性.当前,各类匿名保护方案以实现所有用户等程度模糊为主,缺乏考虑用户的个性化隐私保护需求.因此,下一步,我们将继续就社交网络的个性化隐私保护方案展开深入研究. [1]Liu Peng, Li Xianxian. An improved privacy preserving algorithm for publishing social network data[C] //Proc of 2013 IEEE HPCC&EUC. Los Alamitos, CA: IEEE Computer Sociaty, 2013: 888-895 [2]Peng Wei, Li Feng, Zou Xukai, et al. A two-stage deanonymization attack against anonymized social networks[J]. IEEE Trans on Computers, 2014, 63(2): 290-302 [3]Zhou Bin, Pei Jian. Thek-anonymity andl-diversity approaches for privacy preservation in social networks against neighborhood attacks[J]. Knowledge and Information System, 2011, 28(1): 47-77 [4]Yuan Mingxuan, Chen Lei, Yu P S, et al. Protecting sensitive labels in social network data anonymization[J]. IEEE Trans on Knowledge and Data Engineering, 2013, 23(3): 633-647 [5]Gong N Z, Talwalkar A, Mackey L, et al. Jointly predicting links and inferring attributes using a social-attribute network (san)[C] //Proc of the 6th SNA-KDD. New York: ACM, 2012 [6]Liu Xiangyu, Wang Bin, Yang Xiaochun. Survey on privacy preserving techniques for publishing social network data[J]. Journal of Software, 2014, 25(3): 576-590 (in Chinese)(刘向宇, 王斌, 杨晓春. 社交网络数据发布隐私保护技术综述[J]. 软件学报, 2014, 25(3): 576-590) [7]Guo Longfei. A study on the dynamic influence and behavior regularities of user’ privacy concern about social network[D]. Beijing: Beijing University of Posts and Telecommunications, 2013 (in Chinese)(郭龙飞. 社交网络用户隐私关注动态影响因素及行为规律研究[D]. 北京: 北京邮电大学, 2013) [8]Fu Yanyan, Fu Hao, Xie Xing, et al. Anonymity and privacy-protecting for social network[J]. The Communications of the China Computer Federation, 2014, 10(6): 51-58 (in Chinese)(付艳艳, 付浩, 谢幸, 等. 社交网络匿名与隐私保护[J]. 中国计算机学会通讯, 2014, 10(6): 51-58) [9]Zou Lei, Chen Lei, Özsu M T. K-automorphism: A general framework for privacy preserving network publication[J]. Proceedings of the VLDB Endowment, 2009, 2(1): 946-957 [10]Cheng J, Fu A W, Liu J. K-isomorphism: Privacy preserving network publication against structural attacks[C] //Proc of the ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2010: 459-470 [11]Zheleva E, Getoor L. Preserving the privacy of sensitive relationships in graph data[G] //Privacy, Security, and Trust in KDD. Berlin: Springer, 2008: 153-171 [12]Campan A, Truta T M. Data and structuralk-anonymity in social networks[G] //Privacy, Security, and Trust in KDD. Berlin: Springer, 2009: 33-54 [13]Wang Rong, Zhang Min, Feng Dengguo, et al. A clustering approach for privacy-preserving in social networks[C] //Proc of ISC’14. Berlin: Springer, 2014: 193-204 [14]Skarkala M E, Maragoudakis M, Gritzalis S, et al. Privacy preservation byk-anonymization of weighted social networks[C] //Proc of IEEE Int Conf on Advances in Social Networks Analysis and Mining. Los Alamitos, CA: IEEE Computer Sociaty, 2012: 423-428 [15]Tassa T, Cohen D J. Anonymization of centralized and distributed social networks by sequential clustering[J]. IEEE Trans on Knowledge and Data Engineering. 2013, 25(2): 311-324 [16]Yang Bin, Sato I, Nakagawa H. Privacy-preserving EM algorithm for clustering on social network[C] //Advances in Knowledge Discovery and Data Mining. Berlin: Springer, 2012: 542-553 [17]Han Qilong, Zhou Hongbin, Pan Haiwei, et al. Research on spatio-temporal object graph clustering algorithm based on structure and attribute[J]. Journal of Computer Research and Development. 2013, 50(增刊): 154-162 (in Chinese)(韩启龙, 赵洪斌, 潘海为, 等. 基于结构-属性的时空对象图聚类算法的研究[J].计算机研究与发展, 2013, 50(Suppl): 154-162) Jiang Huowen, born in 1974. PhD candidate. Associate professor. Student Member of China Computer Federation. His main research interests include privacy preservation and software evolution. Zeng Guosun, born in 1964. Professor and PhD supervisor. Senior Member of China Computer Federation. His main research interests include parallel computing, trusted software and information security. Hu Kekun, born in 1987. PhD candidate. His main research interests include parallel computing and graph big-data processing (5hkk@tongji.edu.cn). A Graph-Clustering Anonymity Method Implemented by Genetic Algorithm for Privacy-Preserving Jiang Huowen1,2,3, Zeng Guosun1,3, and Hu Kekun1,3 1(DepartmentofComputerScienceandTechnology,TongjiUniversity,Shanghai200092)2(CollegeofMathematics&ComputerScience,JiangxiScience&TechnologyNormalUniversity,Nanchang330038)3(KeyLaboratoryofEmbeddedSystemandServiceComputing(TongjiUniversity),MinistryofEducation,Shanghai200092) Clustering anonymity is a typical kind of privacy preservation scheme for social network data-publishing, which is based on graph-clustering. Graph-clustering is a kind of NP-hard combinatorial optimization problem and it’s appropriate to use search optimization algorithm. While, the existing graph-clustering anonymity methods are lack of heuristic search algorithm. Therefore, in this paper, a graph-clustering anonymity method implemented by genetic algorithm is proposed. Firstly, the population is initialized by pre-dividing the nodes based on greedy clustering strategy. Then the individual fitness function is defined based on the relation fitting theory. Next, the crossover operator of multi-point dislocation and the mutation operator of exchanging gene-bits are designed respectively, according to individual’s coding feature. The model we presented takes the information of both structure and attribute of nodes into consideration, and the global searching of genetic algorithm can guarantee good quality for graph-clustering. Therefore, the method can provide great privacy preservation. Experimental results also demonstrate that our method is effective in improving the clustering quality and reducing the loss of information. social network; graph-clustering; privacy preservation;k-anonymity; genetic algorithm 2016-06-16; 2016-08-12 国家自然科学基金项目(61272107,71561013);华为创新研究计划项目(IRP-2013-12-03);高效能服务器和存储技术国家重点实验室开放基金项目(2014HSSA10) 曾国荪(gszeng@tongji.edu.cn) TP309 This work was supported by the National Natural Science Foundation of China (61272107,71561013), the Huawei Innovation Research Program (IRP-2013-12-03), and the Project Funded by the State Key Laboratory of High-End Server & Storage Technology (2014HSSA10).


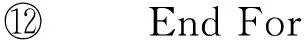





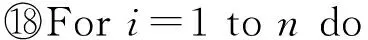
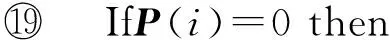
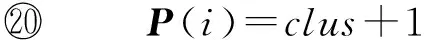



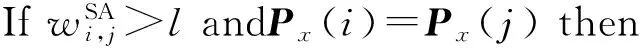


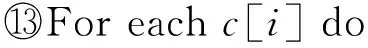
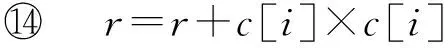










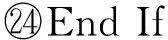



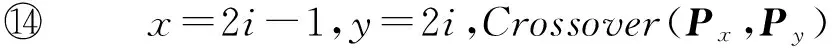
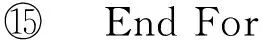


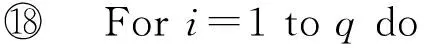
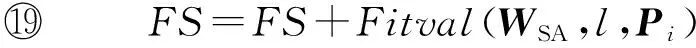





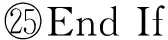

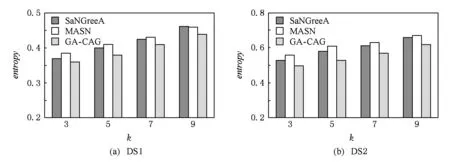
4 实验与结果分析
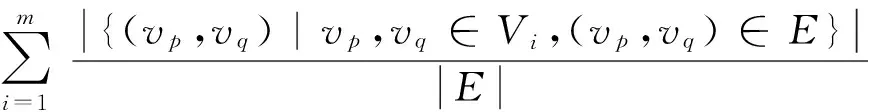
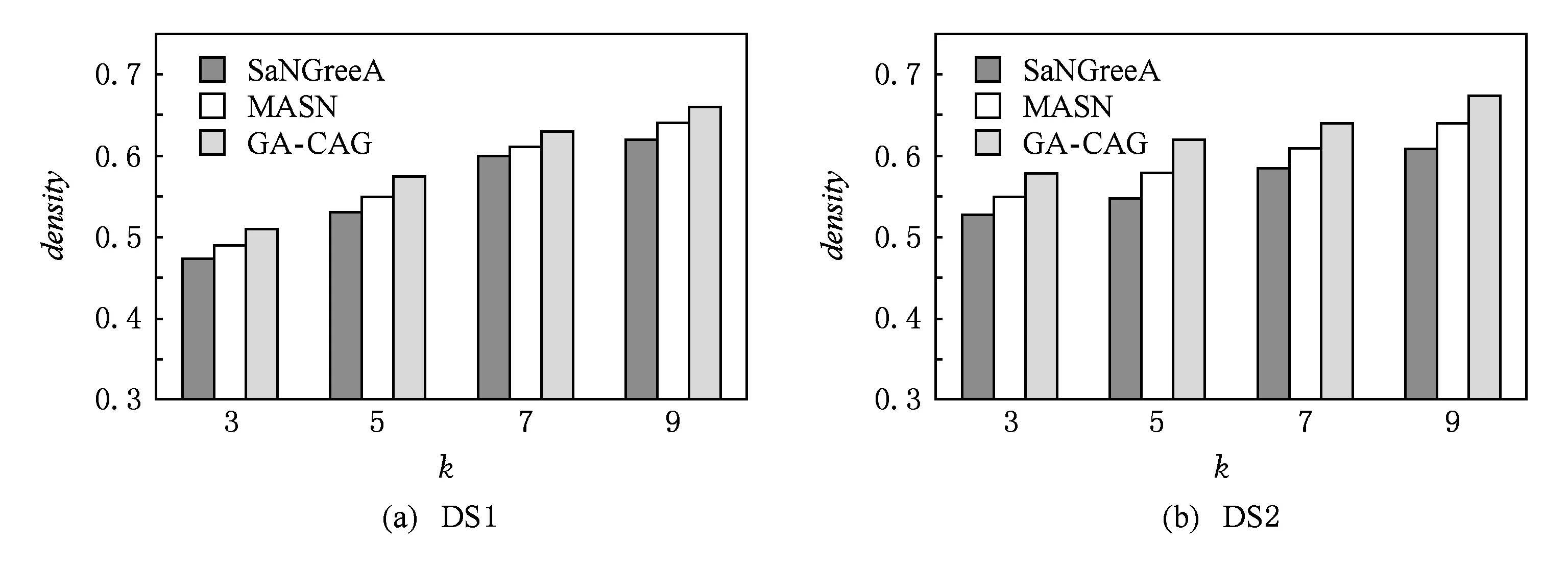
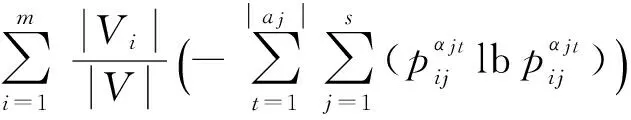



5 结束语




