基于云计算服务的安全多方计算

蒋 瀚 徐秋亮

(山东大学计算机科学与技术学院 济南 250101) (jianghan@sdu.edu.cn)



基于云计算服务的安全多方计算

蒋 瀚 徐秋亮

(山东大学计算机科学与技术学院 济南 250101) (jianghan@sdu.edu.cn)

云计算的出现及迅速发展，使得安全多方计算模型面临结构上的变化.云计算资源的引入，使得安全计算的计算任务、参与方、计算执行的外部环境变得多样和复杂.利用强大的云计算资源来设计、实施安全多方计算协议，成为安全多方计算领域一个新的研究课题.云计算环境为安全多方计算的实施提供了条件，同时但也带来新的挑战.对云环境下通用安全多方计算协议的研究进行了梳理和分析，给出一个较为清晰的发展脉络，对一些基于云的典型特定安全多方计算协议做了简要介绍，并对目前云中安全多方计算存在的问题及未来研究的方向提出了自己的见解.

安全多方计算；云计算；云辅助安全多方计算；安全外包计算

2006年3月亚马逊推出Web服务(Amazon Web services, AWS),2006年8月Google在搜索引擎大会上首次提出“云计算”的概念.之后，云计算的发展迅速形成燎原之势，并引发了第三次信息技术革命的浪潮.

美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)定义云计算是一种按使用量付费的模式，这种模式提供可用的、便捷的、按需的网络访问，进入可配置的计算资源共享池(资源包括网络、服务器、存储、应用软件、服务)，这些资源能够被快速提供，只需投入很少的管理工作，或与服务供应商进行很少的交互.从这个定义中可以看出，在云计算环境中，用户的数据和计算都被移植到一个外部的、虚拟化的“云端”，虽然这种计算模式可以简化用户对信息系统的维护工作，但同时也为信息安全带来新的挑战.

云计算面临的主要安全风险是数据的泄漏、丢失以及隐私泄漏，因此从信息安全的角度，比之传统互联网环境，我们更加需要对数据的机密性、完整性以及隐私性等进行保护.不同于传统的计算场景，云服务用户需要把数据和计算外包给云，因此将失去对资源的完全掌控权.如何利用密码技术解决这种新形势下的信息安全问题，成为云计算研究领域目前最为迫切、最被关注的问题之一.

安全多方计算(secure multi-party computation, SMPC)是解决云计算安全的关键技术之一.在安全多方计算场景中，持有秘密输入的两方或者多方，希望共同计算一个函数并得到各自的输出，在这个过程中，除了得到应得的输出(及可以由输出推导而来的信息)之外，参与方得不到任何额外信息.安全多方计算的这一特点，对于云计算的安全保障有得天独厚的优势.

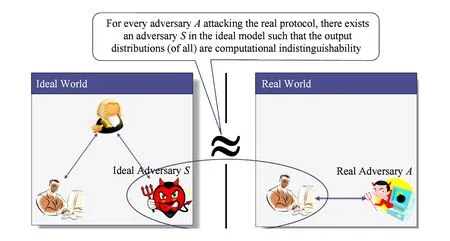
Fig. 1 IdealReal simulation paradigm.图1 理想现实模拟范例

安全多方计算自20世纪80年代由姚期智提出[1]之后，经过几十年的研究，积累了丰富的理论成果，促进了零知识证明、不经意传输、秘密共享等密码学基础原语的发展，奠定了安全协议可证明安全理论基础，极大地推动了现代密码学进展.而在当前云计算广泛应用与发展的新背景下，安全多方计算同样构成云计算环境下应用密码学的理论基础，其安全模型的定义及安全性证明的方法是各类安全协议的共用技术，对一些特定问题安全计算高效实现的研究，则具有重要应用意义.

1 基于云的通用安全多方计算

因为任意可计算的函数都存在一个与之等价的电路，因此通过对电路门的依次安全计算可以解决任意可计算函数的安全计算问题，以此为基础的安全计算协议一般称为通用的安全多方计算协议.

通用的安全多方计算协议虽然可以解决一般性的安全多方计算问题，但是计算效率很低，尽管近年来研究者努力进行实用化技术的研究，并取得一些成果，但是还不能真正实用.

安全多方计算协议的执行会受到某个外部敌手或者某些内部参与方的攻击，因此，在安全多方计算的安全模型中，定义了一个敌手，这个敌手可以控制一个腐化的参与方子集，这种定义方式涵盖了外部攻击、内部攻击及各类合谋攻击的场景.而敌手类型按照行为可以分为半诚实的、恶意的及隐蔽的等.

通用安全多方计算效率较低是由2个主要因素叠加而成的：1)为了解决通用性而将函数运算分解为电路门运算；2)为了抵抗敌手的攻击而依次对每个电路门实施安全计算.而云计算的出现改变了现有的计算模式，为提高通用安全多方计算效率提供了一些新的可能性.既然云作为一种强大的外部计算资源，那么我们完全可以将安全多方计算中的那些复杂的计算任务安全外包给云，从而极大地简化参与方的计算负载，变相提高协议的计算效率.

在云计算概念出现之前，Feige等人就基于第三方服务器，提出了对安全两方计算的一个扩展[2]：除了2个参与方Alice和Bob之外，增加了一个称为Carol的服务器，用于执行协议的相关操作.该协议的通信模式是“最小”的：Alice和Bob协商(或被给定)一个秘密的随机串，然后他们每人向Carol发送一个消息，这个消息实际是他们利用自己的秘密输入和随机值计算出来的.基于从Alice和Bob收到的消息，Carol计算函数值并宣布计算结果.注意在这种模式下，计算结果是盲化的，Carol不能得到Alice和Bob输入的任何知识.

一般来说，通用的安全多方计算协议主要有3类，基于Yao混乱电路的构造方法[1]、基于秘密分享的构造方法[3]以及基于同态加密的构造方法[4]，下面分别基于这种分类来介绍云中的通用安全多方计算协议.

1.1 云中基于Yao混乱电路的安全两方计算协议

基于Yao混乱电路的安全两方计算协议将任意的功能函数看作是一个等价的逻辑电路，由基本的与门、或门、非门组成，而协议的参与方分为电路生成方和电路计算方.最初的Yao协议[1]，对于每一个基本的逻辑电路门，电路构造方针对电路门的每一条输入输出线上的真值选择一个随机数与之对应.而对于该逻辑电路的计算真值表，将2条输入线上的输入真值对应的随机数作为密钥，利用一个对称加密算法，双重加密输出线上输出真值对应的随机数，以构造一个混乱表.随后，电路构造方将以自己实际输入对应的随机数发送给电路计算方，然后通过一个不经意传输协议，把与电路计算方实际输入真值对应的随机数发送给电路计算方.电路计算方拿到2个随机数后，作为解密密钥，双重解密混乱表里的密文，得到唯一正确的、与输出真值对应的随机数.如果该逻辑门是最终的输出门，电路计算方通过查询输出线的真值-随机数对应表，可以得到最终输出的真值.可以看到，在基于Yao混乱电路的安全两方计算协议中，电路生成和电路计算都是复杂的计算任务.

2011年Kamara等人首先研究了将基于Yao混乱电路的通用安全多方计算协议中参与方的复杂计算任务外包给服务器[5].在他们的设定中，除了要计算函数的参与方之外，还有一个不可信的服务器(云)，该服务器：1)没有函数的输入；2)得不到函数的输出；3)具备强大(但是有界)的计算资源.这种设置被称为服务器辅助的安全多方计算(或云辅助的安全多方计算).虽然这篇文章的动机不同于Feige等人[2]的工作，但他们的想法类似.

在考虑外包场景时，电路生成或计算均可以外包给云服务器，将任务外包出去的参与方即称为外包方，而其他参与方即为非外包方.Kamara定义的效率目标非常明确，就是计算任务外包之后，外包方的计算量、通信量只与他的输入输出相关，而与要计算的函数规模无关.这个目标事实上已经最小化了外包方的工作量，因为即使在理想世界中，参与方的计算量、通信量也与他的输入输出相关，因为他至少需要向可信第三方上传输入，同时要从可信第三方获得输出.

为了安全地实现这一效率目标，Kamara等人首先提出了服务器(云)辅助安全多方计算的形式化定义，在他们的定义中，云服务器被看作一个特殊的参与方，它拥有强大的计算能力，但是没有输入输出，这一点本质上没有改变安全多方计算的定义.但是不同于传统的恶意敌手攻击下的安全模型，在Kamara等人的定义安全模型上，要求普通参与方与服务器之间不存在合谋.他们这样规定的原因在于，依照安全多方计算的敌手模型，相互合谋的参与方事实上是由一个敌手刻画的，因此他们退化成一个参与方.如果允许普通参与方与服务器合谋，那将违背外包计算的效率目标.举例来说，当电路计算任务被外包给云服务器时，如果存在一个电路生成方(非外包方)可以与云服务器合谋，那么云辅助的安全多方计算协议将退化成一个安全两方计算协议，而且一方(电路计算方)的计算效率仅与他的输入输出有关.而Damgård等人在文献[6]中指出，达到该复杂度的安全两方计算协议，只能通过全同态加密实现(也就是说无法通过混乱电路实现).鉴于文献[5]的方案是基于Yao混乱电路构造的，因此为达到效率目标，Kamara等人在安全模型中引入了额外的假设：1)云服务器是恶意的但是不与其他参与方合谋，其他参与方是半诚实的；2)至少有一个参与方不是恶意的，云服务器是半诚实的.

很明显，Kamara等人的非合谋模型相对于标准恶意模型是较弱的，但是与半诚实模型相比则更强，而且也有着广泛的应用背景，在文献[5]中，基于他们定义的安全模型，Kamara等人构造了一个电路计算任务外包的服务器辅助安全多方计算协议.随后Kamara等人在工作[5]的基础上，针对安全函数计算(secure function evaluation, SFE)问题，提出云辅助的安全函数计算的概念[7]，并构造了高效的单一服务器辅助的安全函数计算协议.此外，该文还通过扩展云辅助模型，实现了安全函数计算的公平性.

Kamara等人的上述工作奠定了基于Yao混乱电路的云辅助安全多方计算协议的基础.此后，基于特定的应用背景，不同的外包计算任务、及不同服务器的数量，又出现了一些研究成果.

随着便捷移动设备的不断推广，在这些计算能力有限的设备上进行复杂运算成为一个新的广受关注的研究方向.Carter等人研究移动设备的外包安全函数计算问题[8]，事实上，他们的方案是基于Cut-and-Choose技术的Yao混乱电路两方安全计算协议的，他们将移动设备看作电路计算方，将电路计算任务安全外包给云服务器.在基于Yao混乱电路的通用两方安全计算协议中，Cut-and-Choose技术用于实现抵抗恶意敌手攻击，电路生成方需要构造多个混乱电路的副本，供电路计算方选择进行检测或计算.虽然Cut-and-Choose技术有效提高了恶意敌手下安全两方计算的效率，但协议参与方仍需要完成大量的计算任务，诸如多个电路副本的构造、输入一致性检测、混乱电路相关密钥传输、电路计算等.

文献[8]针对基于Cut-and-Choose技术的Yao混乱电路两方安全计算协议中不同的计算任务，提出了在云环境下实现数据隐私性保护的实现机制.具体地，针对混乱电路密钥传输问题，该文提出外包茫然传输机制，旨在将茫然传输过程中涉及到的复杂计算任务外包给云服务器.针对混乱电路的正确性检测以及电路生成方输入一致性检测问题，该文给出了外包的电路正确性检测和输入一致性验证机制.该验证机制完全由云服务器执行，既避免了恶意的电路生成方通过恶意构造混乱电路从而获取对方输入的恶意行为，也使得作为电路计算方的移动设备不需要耗费过多的计算量.此外，该机制也有效地阻止了云服务商的不诚实行为，迫使云服务器必须返回正确的验证结果.针对电路计算问题，在保证输出信息保密的前提下，云服务器完成所有计算电路的计算和输出一致性验证，最后参与方输出各自的输出.该文章给出了外包协议的性能测试数据，协议的运行时间和带宽分别降低了98.92%和99.95%.为了更好地说明云辅助安全计算协议的实用性，文章针对Dijkstra’s最短路径算法实现了有效的外包转换，为如何设计隐私保护的导航应用系统指明了方向.

与文献[8]中构造的场景不同，Carter等人随后将移动设备设定为混乱电路生成方，并将电路的生成任务安全外包给不可信的云服务器[9].虽然只是角色的转换，但是外包协议的设计和安全性证明都具有很多的不同.混乱电路的生成外包主要运用到2-Universal Hash Function技术，而且协议过程中也避免了外包茫然传输机制的使用，从而使得电路生成方的计算复杂度与电路大小不相关.考虑到安全性，该文首次考虑了一种不同于文献[5]中非合谋假设所预设的合谋场景，即允许电路生成方(外包方)与云服务器合谋，并形式化地证明了在该合谋场景下，所设计的外包安全两方计算协议的安全性.此外，针对某些具体的函数，该文给出了上述协议的性能评估.这些函数主要包括海明距离计算、矩阵相乘、Dijkstra算法、RSA函数等，主要思想是针对这些函数对应的电路构造，比较计算外包前后在移动设备上需要执行的时间和带宽.测试结果显示，借助于云计算的辅助，移动设备的效率得到明显的提高.

以上工作主要考虑单一云服务器辅助模型，Kerschbaum等人针对Yao混乱电路的外包计算，将计算分给2个或多个相互独立的服务器，这些服务器在计算时合作但是不共享数据[10].该文提出了茫然外包计算的概念，即一个服务器不知道其他服务器是否参与外包计算，并基于格密码构造了一个混乱电路生成外包方案，使得电路生成效率得以提高，但是并不增加电路的计算量.该文主要实现以下3种茫然性，即输入输出茫然性、函数茫然性以及外包茫然性.此外，针对Ajtai和SHA-3密码学Hash函数，秘密分享的生成和组合问题，作者给出了具体的性能测试，结果显示外包方案的效率较之于参与方本地实现，有明显的提高.

随着云存储的不断发展，在不同的应用中重复使用云中的数据也日益成为信息共享的发展趋势.Mood 等人研究了安全函数计算过程中加密数据的再次使用问题[11].因为移动设备上的操作具有连续性，所以将计算过程中的状态信息存储下来，在其他计算需要的时候重新利用，可以使得效率大大提升.该文针对基于Yao混乱电路的函数计算问题，研究如何重复使用混乱电路计算过程中的加密值，从而降低重复操作.该文提出PartialGC的概念，基本思想是将一个大的程序分割成许多小片，并在混乱电路计算过程中引入交互式IO操作，这也是在基于Cut-and-Choose技术的混乱电路安全计算问题中首次允许交互式IO操作.

1.2 云中基于秘密共享的安全多方计算协议

在基于秘密共享的安全多方计算协议中，任意的功能函数被看作是一个算法电路，由基本的加法门和乘法门构成.对于每个基本的运算门，电路的输入以一种秘密共享的方式分享于各个协议的参与方，而协议的参与方以共享份额作为输入，针对加法门和乘法门的不同，执行不同的交互协议，完成电路门的计算，而计算结果(加法和或者乘法积)，也是以一种共享份额的形式，分享于参与方.可以看到，在基于秘密共享的安全多方计算协议中，加法门和乘法门的交互计算是其中复杂的计算任务，它即需要参与方做大量的计算，又需要参与方之间多次的交互.

Jakobsen等人研究将基于秘密共享的安全多方计算协议中n个参与方之间的算法电路门计算的交互协议，外包到m个云服务器(文中称为Workers)来做[12].在他们的安全模型中，云服务器可以是不可信的，但前提是至少有一个服务器是诚实的，并且不需要文献[5]中规定的非合谋这一弱安全假设.他们的安全目标是同时满足隐私性和正确性要求，即每个参与方的输入(对其他用户和每个云服务器)是保密的，同时每个用户都能得到正确的结果，即使恶意的云服务器依然无法篡改每个用户应该得到的输出.而他们协议的效率目标是参与方的通信复杂度最小(仅上传输入和接收输出)，同时也尽可能减少所有服务器的工作量.

文献[12]分别给出了半诚实参与方和恶意参与方模型下安全的方案.具体来讲，半诚实参与方协议较为平凡，主要分为3个步骤：1)每个用户通过秘密分享方案将自己的输入和一个盲化值(其中盲化值用于盲化功能函数的输出结果，从而功能函数的输出对云服务器来说是保密的)分享给m个Workers；2)在这些Workers之间运行一个现有的安全多方计算协议，该协议的运行结果为每个用户的盲化输出(用户的真实输出加上他的盲化值);3)每个Worker将盲化输出值分享给用户，每个用户使用来自于各个Worker的份额恢复出自己的盲化输出，减去自己的盲化因子便得到各自的输出.

但是对于恶意敌手模型，上述协议有3个问题需要解决：1)恶意的Worker可能会篡改来自用户的输入，因此，需要在各个Worker拿到各自输入之后，先运行一个校验协议，来确认每个Worker输入到Worker之间的安全多方计算协议是正确的输入值;2)恶意的服务器在输出的时候，可能会输出错误的结果;3)协议的公平性未得到保障，即由于Worker或者参与方发现错误而终止协议，会导致有的用户得到了输出，有的用户没有得到输出.对于2),3)，可以通过修改Worker之间安全多方计算的功能函数使得每个Worker都得到全部用户的盲化输出，之后都向全部用户发送各自的盲化输出，这样，用户可以校验是否来自每个Worker的输出都相同.这样既可以发现Worker的恶意行为，又能保证要么所有的用户都拿到输出，要么任何一个用户都拿不到输出.

1.3 云中基于同态加密的安全多方计算协议

在传统的安全多方计算现实世界的协议中没有第三方的辅助，而在云计算环境下，云服务器可以视为一个第三方.如果把云服务器看作完全可信的，那么只要保证有一个可信信道，那就与理想世界完全相同，参与方将输入发送给云服务器，由云服务器来计算功能函数，并将计算结果返回给各参与方即可.但是云服务器，特别是公共云服务器，不是被完全信任的，云计算要求保证参与方数据对云服务器的机密性.当全同态加密方案出现之后，参与方将各自输入利用全同态密码算法加密之后，上传到云服务器，由云服务器对同态密文进行计算并返回结果，从而可以保证数据机密性.

上述平凡的思想存在一个问题，那就是全同态加密方案一般是有一对公私钥，而在安全多方计算中有多个参与方，全同态加密方案的私钥不能被任一个参与方掌握，因此，Asharov等人利用门限全同态加密方案(threshold fully homomorphic encryption, TFHE)，将同态私钥共享于所有参与方，从而构造了一个云辅助的安全多方计算协议[13].具体来说，在运算之前，各参与方运行一个密钥生成协议共同产生方案的公钥，并且保留各自关于私钥的秘密分享份额；然后各方将自己的数据加密，上传到云服务器，由云服务器对密文进行同态计算并返回结果；最后各方运行解密协议对此结果进行解密以得到最终的计算结果.

由于通用的门限全同态加密方案相对低效，Asharov等人基于文献[14-15]中的FHE方案给出了相对比较高效的TFHE方案的构造.文献[14-15]中的FHE方案为密钥加同态的，即多个私钥的和所对应的公钥即为这些私钥所对应的公钥之和；使用此公共公钥加密所得到的密文，可以使用上述每个私钥分别进行部分解密，然后利用这些部分结果解密出明文.Asharov的TFHE方案使用2轮即可产生所需要的公钥(公钥用于加密)与计算密钥(计算密钥用于对密文进行计算)：第1轮各方产生公共公钥与各自的私钥份额，第2轮各方产生公共的计算密钥；并且使用一轮即可完成解密协议.基于此TFHE方案，他们又构造了4轮的基于云服务器的安全多方计算协议.第1轮，各参与方运行TFHE密钥生成协议的第1轮并产生公共的公钥；第2轮，各方运行TFHE密钥生成协议的第2轮，产生公共的计算密钥，并利用第1轮的公共公钥将各自的输入加密，广播出去；第3轮，云服务器拿到方案的公钥、计算密钥以及所有的密文之后自行算出计算结果的密文然后将此密文广播；最后，各参与方拿到计算结果的密文后运行解密协议即可得到真正的计算结果.在上述过程中，各参与方仅需要执行与TFHE相关的计算，而真正的计算任务则在云服务器进行.因此对各参与方来说，计算量不是很大.

该协议可以被证明在半恶意模型下安全，即模型中敌手基本遵照协议进行，但是可能会根据自己的视图恶意地产生运算中使用的随机数.因此，云服务器可以仅利用简明非交互零知识论证系统(succinct non-interactive argument systems)，而不使用掷币协议来证明它在诚实地执行协议，从而将其转化为恶意敌手模型下安全的协议，转化后的协议仍然可以在4轮内完成.

在文献[13]所考虑的场景中，参与方需要在每次计算时，与参与这次运算的用户共同临时产生本次计算所需要的全同态密钥.但在实际应用中，用户更倾向于在系统建立之初就产生自己的公私钥对，并长期使用.因此，López-Alt 等人提出了动态多方计算(On-the-Fly Multiparty Computation)的概念[16].在他们所考虑的场景中，用户各自拥有长期的公私钥对，并利用自己的公钥加密自己的数据，然后将密文上传到云服务器；当有计算任务需要执行时，云服务器利用相应的密文进行计算；最后，在计算完成后云服务器与相关的用户共同执行多方解密协议，用户得到最终结果.在解密过程中，要求计算量与具体计算任务无关.

在文献[16]中，López-Alt 等人提出了多密钥全同态加密方案(multikey fully homomorphic encryption, MFHE)，并基于此构造了On-the-Fly Multiparty Computation.本质上来说，MFHE还是一个全同态加密方案，但是运算可以在利用不同公钥加密的密文之间进行；运算后的结果密文大小与运算电路以及运算中使用的密文个数无关，而仅与运算中涉及到的公钥数量相关；要解密运算得到的结果密文，需使用涉及到的公钥所对应的私钥共同运算进行解密.López-Alt 等人观察到NTRU加密方案[17-18]本身就在一定程度上满足了上述要求，因此，他们使用了文献[14-15]中的方法将NTRU转化为MFHE方案.而在他们的On-the-Fly Multiparty Computation协议中，使用到了MFHE方案的这一特性，并通过一些合适的零知识证明系统与掷币协议，将协议编译成恶意敌手下安全的.

前面的工作对于解决云环境下多方计算的安全性问题有着很大的理论意义，但是他们所构造的协议的效率却受到了全同态加密方案的制约.因此Peter等人仅利用加同态给出了一个实用的解决方案[19].Peter等人所考虑的场景与动态安全多方计算的场景类似，但是在他们的场景中，用户并不需要交互式地对结果密文进行解密，与之相反，用户仅需从云服务器将结果密文下载然后自行解密即可.为了达到这样的效果，他们的协议中使用了一个带有主私钥的加同态加密方案[20](下文称之为BCP方案，BCP方案除了用户的公私钥对之外，系统中还存在一个主私钥，主私钥可以用来解密在公开参数下使用任意公钥加密的密文)，并假设用户使用2个不合谋的云服务器，一个云服务器掌握加密方案的主私钥，可以解密所有出现的密文；另一个云服务器保存所有的用户密文.在用户将数据上传之后，二者可以运行安全多方计算协议自行计算出结果.具体来说，在系统建立阶段，其中一个服务器S产生BCP方案的主私钥与公共参数，随后它公开此公共参数并自己保留主私钥；然后用户利用此公开参数产生自己的公私钥对，利用公钥加密自己的数据，并将密文上传到另一个云服务器C；当有计算任务需要执行时，云服务器C和云服务器S共同完成此计算：1)C和S运行一个子协议，将所有用到的密文转化成在某个特定公钥下加密的密文，由于所使用的加密方案为加同态的，所以此时C和S可以利用文献[4]中的基于加同态的安全多方计算方法在密文下进行函数运算，并保证C得到运算结果在特定公钥下的密文；2)C和S执行另一个子协议，将此密文转化成参与用户所对应的公钥下的密文；3)用户仅需下载相应密文即可得到计算结果.在上述过程中，用户仅需执行上传和下载操作，并不需要进行额外的交互.

文献[19]方案是在半诚实敌手模型下安全的，所有的用户，包括云服务器，均为半诚实的.为了说明所构造的协议的高效性以及实用性，作者还在文中给出了协议各部分的实际运行时间，以及2个特定应用协议的总体运行时间(隐私保护的人脸识别以及隐私保护的智能测量).从这些实验数据可以看出，文中的协议确实有很强的实用性.

1.4 云中通用安全多方计算协议的分析比较

从现有的研究结果可以看到，基于同态加密的云辅助安全多方计算，协议结构最为简单，它对整个功能函数进行密态计算，避免了将任意功能函数转化为相应的电路，然后依次对电路门进行安全计算.事实上，它将对任意功能函数的计算能力，封装到全同态加密方案中.这类方法受到了全同态密码算法的限制，目前的全同态密码事实上也是针对电路设计的，并且效率完全无法实用.基于同态加密的云辅助安全多方计算真正实用还有待全同态加密算法进一步突破.但是，如果我们的目标不是解决所有的功能函数，对于某些特定的实际的计算任务，可能只需部分同态密码算法即可完成，这时完全可以得到真正实用的方案，但这不是通用的方案.

而基于Yao混乱电路所构造的云辅助安全多方计算协议不需要使用低效的非对称密码操作，但是也存在2点不足：1)较之于基于同态加密的方案，其安全模型有所降低.因为在标准SMPC模型下，不诚实参与方是允许合谋的；然而上述安全模型要求不诚实参与方是不能合谋的.2)基于Yao混乱电路的协议要求至少一个非服务器参与方必须做与电路大小线性相关的工作；而在基于同态加密的方案中，所有非服务器参与方只需做与输入输出相关的工作.

基于秘密分享的云辅助安全计算协议，可以完全转化为标准的安全多方计算协议，不需要在安全模型上做出进一步的改进，但是协议效率低.

2 基于云的几类特定的安全多方计算协议

通用的云辅助安全多方计算协议虽然也能用于构建特定应用的外包方案，但其效率较低.因而设计针对于特定的应用设计专用的高效协议，逐渐受到研究者的重视.比如云环境下基于安全多方计算技术的秘密集合求交(private set intersection, PSI)、隐私保护的信息检索(private information retrieval, PIR)、数据库查询和推荐系统等具体应用协议.

2.1 云辅助秘密集合求交

Freedman首先提出秘密集合求交协议[21].在秘密集合求交协议中，双方希望得到他们所持有集合的交集，同时不向对方泄漏关于自己所持有的那个集合的任何信息.秘密集合求交协议在现实世界中有广泛的应用，如数据挖掘、社交网络分析及健康数据处理中的隐私保护等.

云辅助的集合求交方案，将集合求交任务交给云服务器，同时保证隐私性.Kerschbaum提出了抗合谋的外包秘密集合求交协议[22]，即用户分别将自己的集合加密上传到服务器之后，服务器计算得到用户集合的交集并分别返回给用户，在服务器和任意一个用户合谋的情况下，该协议依然是安全的.文献[22]中提供了2个外包协议，即服务器可获得交集大小的协议，服务器无法获知任何信息的协议.随后，Kerschbaum又在文献[23]中提出另一种解决方案，在该方案中用户不是直接将集合的密文外包给云服务器，而是将集合转换成相应的布隆过滤器(Bloom filter)，之后将布隆过滤器加密后外包给服务器.云服务器利用加密的布隆过滤器进行求交操作，因而，为了获得求交结果用户不得不自己保存整个集合的副本.

在文献[24]提出的协议中，用户首先对集合中的每个元素做一次Hash之后，再加上一个随机值，以此来保证隐私性.随后将处理后的集合上传到云服务器，由云端在散列值下进行交集操作.文献[25]类似于文献[24]的方案，但提供了可验证机制.文献[24-25]都存在相同的信息泄漏量较大的问题.具体来说，服务器可获知求交结果集合的基数；并且如果2个集合都和第3个集合求过交集，那么这2个集合是否有交集这一信息也被服务器知道了.

Kamara等人提供了较为完善、多个不同安全模型下可证明安全的云辅助集合求交方案[26](半诚实的和恶意的服务器)，同时给出了保证公平性和能够隐藏交集大小的方案.具体来讲，在半诚实模型下，用户通过一个伪随机函数对集合每个元素进行盲化，再利用一个伪随机置换将集合内元素顺序打乱.随后将处理过的集合发送给云服务器，服务器只需直接在集合密文上做“求交”操作，而不需要任何的密码学操作.之后服务器将所得交集的密文返回给用户，而用户利用伪随机函数的逆过程，获得交集的明文.在恶意服务器的模型下，为了防止服务器返回错误的求交结果，在半诚实模型下安全的协议的基础上，用户将集合的每个元素复制λ份，并在每一份后面联接上相应的序号.当服务器返回求交结果后，用户只需检查每个元素的序号是否完备，便可知道服务器是否返回了错误结果.

Abadi等人提出了一个多用户外包秘密集合求交协议[27]，允许无限多个用户将自己的集合加密后，上传到云服务器，只有在得到每个用户的允许后，服务器才能够求这几个用户的交集.另外，每个用户在将他的集合外包给服务器之后，便可和其他不同集合的用户进行求交操作(即和不同用户的集合进行求交，不需要再用不同的密钥进行重加密).在安全性方面，服务器无法获得任何信息.

2.2 隐私保护的信息检索及其外包

Chor等人最先提出隐私保护的信息检索[28].隐私保护的信息检索是一种隐私增强技术，它可以使客户以一种隐私保护的方式来查询一个数据库.具体来说，它允许客户从一个数据库中检索一些项目，但是不向服务器泄漏任何客户检索项目的信息.隐私保护的信息检索的一个平凡的构造就是将数据库整个下载到客户端进行本地查询，尽管这种方式可以达到理论上的安全性，但是对大数据库来说，需要巨大通信带宽及客户端的存储和计算能力.因此，一个可行的隐私保护的信息检索方案除了需要满足正确性和隐私性需求外，还要求协议的传输量远远小于整个数据库的规模.

隐私保护的信息检索本身就是一个客户端服务器的结构，完全适合云计算的架构，但是传统的隐私保护的信息检索方案遇到云计算海量数据时，云端的计算效率急剧恶化.其原因在于，由于内存空间的限制，在运行该协议的时候需要将大量的数据从硬盘调度到内存，该调度过程(硬盘寻址与读取)造成了极大的负载.Olumofin等人的实验显示[29]，传统隐私保护的信息检模式在数据量增加到TB级别的时候，仅执行云端的计算任务就需要10 min的时间.因而，学者希望针对云计算特定的高性能软硬架构，来设计适应超大规模数据库的隐私保护的信息检方案.主要手段是利用MapReduce[30]范型将大数据库下的查询，分解成多个数据库存储上面的并行子查询，而每个服务器上面子查询，采用传统的隐私保护的信息检索方案即可达到效率要求[31-32].

上述方案都是针对公开数据的隐私保护的信息检索，Jarecki等人提出了外包隐私保护的信息检索[33]的概念：数据拥有者将自己的数据库外包给了云服务商，用户在得到数据拥有者授权后，可以获取服务器上面相应的数据，其安全性要求，只有相应权限的用户可以得到授权，而数据拥有者不知道用户获取了那些数据，同时云服务提供商既不能获知存在其上面的数据信息，也不可知用户查询的具体内容.Huang 等人同时考虑了外包数据库的茫然更新问题[34]，除需保证数据库用户访问模式的隐私性之外，还需要保证数据库本身及其更新模式不被云服务器获取.

2.3 外包数据库查询及安全多方计算

在云计算数据即服务(data as a service, DaaS)模式下，用户将数据库外包到云服务器，随后执行查询操作，并得到相应的查询结果.为了保护敏感数据的机密性，用户需要将数据库加密后，再上传到云服务器，因而，如何在加密的数据上执行检索操作是数据库安全外包中的核心问题.

为了解决在加密数据上的查询问题，一种称为可搜索加密(searchable encryption, SE)的概念被提出，并有大量的构造方案出现.在将可搜索加密方案应用到加密数据库查询协议时，安全多方计算协议是一个重要的工具.例如在Cash等人提出的支持布尔查询的大数据可搜索对称加密方案[35]中，就使用了一个安全两方计算协议，这样既利用了数据拥有者的秘密陷门，又保护了陷门数据的机密性.

从安全多方计算的角度讲，数据库安全外包与检索协议的功能函数分为2个阶段：初始化阶段与检索阶段.考虑到网络状况的限制，协议的设计希望达到最少的交互轮数和最小的通信量.Hazay等人[36]从安全多方计算的角度，在理论上系统地分析了在半诚实模型下，外包数据库查询协议的通信轮数和通信量的下界，并指出为设计出达到该下界的协议，可信的初始化阶段和随机预言机(Random Oracle)是必要的.同时给出了一个达到最小交互轮数和最小通信量的具体协议.

2.4 推荐系统

推荐系统也是一个很重要的多方应用协议.在一个推荐系统中，存在一个服务器与多个客户，服务器利用客户的个人信息为客户推荐他可能需要的内容.推荐系统被广泛的应用在电子商务、社交网络、搜索引擎等应用中，并为人们获取信息带来了极大的便利.在一个没有密码学工具保护的推荐系统中，服务器可以分析掌握用户的消费习惯等隐私信息，同时，恶意的服务器也会向用户推荐一些不正确的内容(如那些用户不需要，但产品供应方付出广告费的内容).

Veugen等人针对推荐系统这一类特殊应用构造一个云辅助的安全多方计算协议[37].同文献[19]类似，作者同样利用2个不合谋的云服务器，具体来说，他们在2个服务器之间运行一个基于秘密分享的安全多方计算协议，而用户仅需在协议执行之初向2个服务器上传秘密分享份额，并在协议完成后下载相应的数据即可.

3 结束语

云计算环境正在逐步带来一种新的资源组织、利用模式，在云计算环境下考虑各种安全协议的设计与实施已成为必然，安全多方计算协议也不例外.针对云计算环境建立新的安全多方计算协议的计算与安全模型是一个迫切的任务.

对于传统的通用安全多方计算协议，安全理论上发展已经较为成熟.而对于云中的安全多方计算，现有的安全模型只是将云服务器看成普通参与方而纳入原有的安全框架下，虽然这样也可以设计和分析云中的安全多方计算协议，但这种方式不自然，反映不出云环境的特点，最终的结果就是设计出的协议只是将计算量迁移到云中，同时为了迁移计算量又带来了相当大的额外计算负载，因此计算负载总量事实上是远高于非云环境中的协议.这种问题的根源在于传统的安全多方计算中理想现实模拟范例中，现实世界中都是平等的参与方，与云环境并不贴合.云作为无输入输出，并且具有超级计算能力的一方，与普通的参与方并不平等.而如果将云看作第三方，因为其不可信，又与理想世界不同，而且第三方与参与方的合谋会带来新的问题.如何合理定义这种介于理想和现实之间的模型来反映云计算协议的特点，是一个需要进一步解决的难点.

随着云计算的不断发展，越来越多不同领域内的应用也逐渐转移到云平台上.针对这些特性找到合适的密码学工具，包括安全多方计算工具是一个新兴的、广泛的研究领域.这些领域应用抽象成数学问题，其对应的功能函数可能有不同的特点，同时这些领域应用可能会要求不同的安全特性.对于这些问题，使用通用的安全多方计算协议效率较低，因此，针对具体问题设计特定的高效安全计算协议，具有很高的应用意义.

综上所述，云不仅仅是一个强大的外部服务器，不仅仅可以作为安全多方计算的一个辅助设施，也应该能够被利用来独立可信地完成某些安全计算任务，另一方面，云本身所需要完成的计算任务，比如保护隐私的数据处理、加密数据的处理等，也应该能够抽象成安全多方计算的任务来完成.云中的安全多方计算，从基础理论到高层的应用，都有广阔的研究空间.

[1]Yao A C C. How to generate and exchange secrets[C] //Proc of the 27th Annual Symp on Foundations of Computer Science. Piscataway, NJ: IEEE, 1986: 162-167

[2]Feige U, Kilian J, Naor M. A minimal model for secure computation (extendedabstract)[C] //Proc of the 26th ACM Symp on Theory of Computing. New York: ACM, 1994: 554-563

[3]Cramer R, Damgård I, Maurer U. General secure multi-party computation from any linear secret-sharing scheme[C] //Proc of the 19th Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2000: 316-334

[4]Cramer R, Damgård I, Nielsen J B. Multiparty computation from threshold homomorphic encryption[C] //Proc of the 20th Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2001: 280-300

[5]Kamara S, Mohassel P, Raykova M. Outsourcing multi-party computation[J/OL]. IACR Cryptology ePrint Archive, 2011 [2016-06-15]. http://eprint.iacr.org/2011/272

[6]Damgård I, Faust S, Hazay C. Secure two-party computation with low communication[C] //Proc of the 9th Theory of Cryptography Conf. Berlin: Springer, 2012: 54-74

[7]Kamara S, Mohassel P, Riva B. Salus: A system for server-aided secure function evaluation[C] //Proc of the 2012 ACM Conf on Computer and communications security. New York: ACM, 2012: 797-808

[8]Carter H, Mood B, Traynor P, et al. Secure outsourced garbled circuit evaluation for mobile devices[J]. Journal of Computer Security, 2016, 24(2): 137-180

[9]Carter H, Lever C, Traynor P. Whitewash: Outsourcing garbled circuit generation for mobile devices[C] //Proc of the 30th Annual Computer Security Applications Conf. New York: ACM, 2014: 266-275

[10]Kerschbaum F. Oblivious outsourcing of garbled circuit generation[C] //Proc of the 30th Annual ACM Symp on Applied Computing. New York: ACM, 2015: 2134-2140

[11]Mood B, Gupta D, Butler K, et al. Reuse it or lose it: More efficient secure computation through reuse of encrypted values[C] //Proc of the 2014 ACM SIGSAC Conf on Computer and Communications Security. New York: ACM, 2014: 582-596

[12]Jakobsen T P, Nielsen J B, Orlandi C. A framework for outsourcing of secure computation[C] //Proc of the 6th Edition of the ACM Workshop on Cloud Computing Security. New York: ACM, 2014: 81-92

[13]Asharov G, Jain A, López-Alt A, et al. Multiparty computation with low communication, computation and interaction via threshold FHE[C] // Proc of the 31st Annual Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2012: 483-501

[14]Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE[J]. SIAM Journal on Computing, 2014, 43(2): 831-871

[15]Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[C] //Proc of the 3rd Innovations in Theoretical Computer Science Conf. New York: ACM, 2012: 309-325

[16]López-Alt A, Tromer E, Vaikuntanathan V. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption[C] //Proc of the 44th Annual ACM Symp on Theory of Computing. New York: ACM, 2012: 1219-1234

[17]Hoffstein J, Pipher J, Silverman J H. NTRU: A ring-based public key cryptosystem[C] // Proc of the 5th Int Algorithmic Number Theory Symp. Berlin: Springer, 1998: 267-288

[18]Stehlé D, Steinfeld R. Making NTRU as secure as worst-case problems over ideal lattices[C] // Proc of the 30th Annual Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2011: 27-47

[19]Peter A, Tews E, Katzenbeisser S. Efficiently outsourcing multiparty computation under multiple keys[J]. IEEE Trans on Information Forensics and Security, 2013, 8(12): 2046-2058

[20]Bresson E, Catalano D, Pointcheval D. A simple public-key cryptosystem with a double trapdoor decryption mechanism and its applications[C] // Proc of the 2003 Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2003: 37-54

[21]Freedman M J, Nissim K, Pinkas B. Efficient private matching and set intersection[C] // Proc of the 2004 Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2004: 1-19

[22]Kerschbaum F. Collusion-resistant outsourcing of private set intersection[C] //Proc of the 27th Annual ACM Symp on Applied Computing. New York: ACM, 2012: 1451-1456

[23]Kerschbaum F. Outsourced private set intersection using homomorphic encryption[C] //Proc of the 7th ACM Symp on Information, Computer and Communications Security. New York: ACM, 2012: 85-86

[24]Liu F, Ng W K, Zhang W, et al. Encrypted set intersection protocol for outsourced datasets[C] // Proc of the 2014 IEEE Int Conf on Cloud Engineering (IC2E). Piscataway, NJ: IEEE, 2014: 135-140

[25]Zheng Q, Xu S. Verifiable delegated set intersection operations on outsourced encrypted data[C] // Proc of the 2015 IEEE Int Conf on Cloud Engineering (IC2E). Piscataway, NJ: IEEE, 2015: 175-184

[26]Kamara S, Mohassel P, Raykova M, et al. Scaling private set intersection to billion-element sets[C] // Proc of the 2014 Int Conf on Financial Cryptography and Data Security. Berlin: Springer, 2014: 195-215

[27]Abadi A, Terzis S, Dong C. O-PSI: Delegated private set intersection on outsourced datasets[C] //Proc of the 2015 IFIP Int Information Security Conf. Berlin: Springer, 2015: 3-17

[28]Chor B, Goldreich O, Kushilevitz E, et al. Private information retrieval[C] //Proc of the 36th Annual Symp on Foundations of Computer Science. Piscataway, NJ: IEEE, 1995

[29]Olumofin F, Goldberg I. Revisiting the computational practicality of private information retrieval[C] // Proc of the 2011 Int Conf on Financial Cryptography and Data Security. Berlin: Springer, 2011: 158-172

[30]Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[C] // Proc of the 6th Symp on Operating System Design and Implementation. San Francisco: USENIX Association, 2004: 107-113

[31]Blass E O, Di Pietro R, Molva R, et al. PRISM-privacy-preserving search in MapReduce[C] //Proc of the 2012 Int Symp on Privacy Enhancing Technologies Symp. Berlin: Springer, 2012: 180-200

[32]Mayberry T, Blass E O, Chan A H. PIRMAP: Efficient private information retrieval for MapReduce[C] //Proc of the 2013 Int Conf on Financial Cryptography and Data Security. Berlin: Springer, 2013: 371-385

[33]Jarecki S, Jutla C, Krawczyk H, et al. Outsourced symmetric private information retrieval[C] //Proc of the 2013 ACM SIGSAC Conf on Computer & Communications Security. New York: ACM, 2013: 875-888

[34]Huang Y, Goldberg I. Outsourced private information retrieval[C] //Proc of the 12th ACM Workshop on Privacy in the Electronic Society. New York: ACM, 2013: 119-130

[35]Cash D, Jarecki S, Jutla C, et al. Highly-scalable searchable symmetric encryption with support for boolean queries[C] // Proc of the Advances in Cryptology (CRYPTO 2013). Berlin: Springer, 2013: 353-373

[36]Hazay C, Zarosim H. The feasibility of outsourced database search in the plain model[J/OL]. IACR Cryptology ePrint Archive, 2014 [2016-06-15]. http://eprint.iacr.org/2014/706

[37]Veugen T, de Haan R, Cramer R, et al. A framework for secure computations with two non-colluding servers and multiple clients, applied to recommendations[J]. IEEE Trans on Information Forensics and Security, 2015, 10(3): 445-457

Jiang Han, born in 1974.Lecturer of Shandong University since 2009. His main research interests include cryptography and information security, especially secure multi-party computation.

Xu Qiuliang, born in 1960. Currently professor and PhD supervisor in Shandong University. His research interests include public key cryptography and multi-party secure computation.

Secure Multiparty Computation in Cloud Computing

Jiang Han and Xu Qiuliang

(SchoolofComputerScienceandTechnology,ShandongUniversity,Jinan250101)

The emergence and rapid development of cloud computing structurally change the computation models of secure multi-party computation. In cloud environment, the computation task, the participants and the external environment of secure multi-party computation are becoming diversified and complicated. Using huge cloud resources to design and implement the secure multi-party computation protocol becomes a new research area. Cloud computing provides the resources to implement secure multi-party computation protocols, meanwhile, it also brings new challenge. In this paper, a survey for generalmulti-party computation in cloud setting, as well as some specific cloud-based secure multi-party computation protocols are given. Also, our opinions of the problem in the current researches and the directions for future works on multi-party computation in cloud setting are proposed.

secure multiparty computation; cloud computing; cloud-assisted secure multiparty computation; secure outsourced computation

2016-06-16；

2016-09-08

国家自然科学基金项目(61572294)；山东大学基本科研业务费专项资金项目(2016JC029)

TP309

This work was supported by the National Natural Science Foundation of China (61572294) and the Fundamental Research Funds of Shandong University (2016JC029).