不同湍流模型在低雷诺数流动中的应用研究
陈立立,郭正
(国防科技大学航天科学与工程学院,长沙410073)
不同湍流模型在低雷诺数流动中的应用研究
陈立立,郭正†
(国防科技大学航天科学与工程学院,长沙410073)
以SD7032翼型为研究对象, 基于求解雷诺平均N-S方程的有限体积法,采用S-A、k-w、SSTk-w、realizablek-ε、transition SST和改进的γ-Reθ,t转捩模型等6种湍流模型, 对雷诺数为203 800时翼型流动进行了数值模拟,评估了不同湍流模型在低雷诺数流动中的升阻特性和收敛情况。结果表明:当不考虑流动转捩时,和其他湍流模型相比,SSTk-w湍流模型计算得到的升阻系数更接近实验值,能够较好地模拟低雷诺数流动。考虑转捩时,改进后的γ-Reθ,t转捩模型的稳定性和收敛性都有较大提升,在小攻角范围内计算结果和实验值吻合。
低雷诺数流动;SD7032翼型;湍流模型;γ-Reθ,t转捩模型
目前,低雷诺数流动是一个比较模糊的范畴,并没有明确的定义。文献[1]给出了低雷诺数翼型的雷诺数范围一般在104~105量级,文献[2]对雷诺数范围为2.5×105~5×105的翼型进行了优化设计,研究对比了低雷诺数翼型的流动特点和差异。刘沛清等通过数值方法研究了低雷诺数下的翼型层流分离泡[3]。低雷诺数有着独特的流动现象,这些现象在宏观上会影响飞机的气动力,因此,必须关注低雷诺数流动的特点。
目前, 工程上常采用雷诺平均方法(RANS)数值模拟低雷诺数流动,主要基于涡黏模型的湍流模型,比如一方程S-A模型、两方程的k-ε模型和k-ω模型等。然而,上述湍流模型是将流动进行了全湍流计算,并未考虑转捩对气动性能的影响,使得阻力计算值与实验值差别较大。为了能准确预测转捩位置,提高计算准确性,2004年,Menter等提出了一种基于动量厚度和间歇因子的γ-Reθ,t转捩模型[4-5]。该模型通过求解间歇因子和临界动量厚度雷诺数,模拟与预测流动转捩,可较好地处理自然转捩、Bypass转捩和分离转捩等现象。该模型的提出者之一Langtry于2009年公布了此模型的经验关联式[6],但该关联式并不具有普适性。Tomac等对不同关联式进行了对比分析,通过优化计算流体力学(computional fluid dynamics,CFD)计算结果和风洞试验数据得到了一组适用于航空领域计算的关联式[7]。但是由于Reθ,t的大小与当地湍流度关系很大,且低湍流度的较小波动都会引起Reθ,t发生较大增加,因此,低雷诺数翼型的湍流度一般小于0.3%。对于雷诺数约为3×105时,根据平板层流边界层理论估算其对应的最大转捩动量厚度雷诺数为500左右,如果直接采用未改进的transition SST模型,得到的转捩动量厚度雷诺数在1 000左右,不符合实际流动状态。因此,本文提出了一种改进的γ-Reθ,t转捩模型来计算低雷诺数翼型流动。
1计算方法
本文计算程序基于求解二维定常雷诺平均的N-S方程,采用空间离散的有限体积法,利用SIMPLE算法求解流场,空间离散格式采用二阶精度,边界条件采用速度入口与压力出口条件。选择采用S-A、k-w、SSTk-w、realizablek-ε、transition SST模型和改进的γ-Reθ,t转捩模型。改进的γ-Reθ,t转捩模型主要是将Michel转捩判据和原始的γ-Reθ,t结合应用,利用Michel转捩判据预估转捩动量厚度雷诺数Reθ,t。利用Tomac提出的经验关系式[7]计算Reθ,c和Flength经验关联值。Reθ,c是边界层内间歇因子开始增加处动量厚度雷诺数,Flength表示转捩区的长度。这样就可以根据不同的流动状态得到适用于该流动的一组经验关联值。
Michel转捩判据是Michel 于1951年提出的一个相当简单的纯经验公式[8],可根据当地边界层动量厚度雷诺数判定流动是否转捩,Michel给出的转捩关系式为
(1)
该公式的雷诺数适应范围为0.1×106≤Rex≤40×106。其中,Rex为基于流向位置的当地雷诺数;Reθ为基于流向位置的动量厚度雷诺数;Retr为转捩处的雷诺数。
Tomac提出的Reθ,c和Flength经验关系式为
(2)
(3)
2SD7032翼型数值分析
本文借助ANSYS Fluent 14.5平台,对雷诺数为203 800的翼型流动进行数值分析,并与Selig的实验数据进行对比[9]。分析对比了不同湍流模型的计算结果。其中,根据不同来流边界条件,将S-A模型分为S-A_MTV和S-A_TVR两种。其中,MTV表示入口边界是湍流修正黏度,TVR表示入口边界是湍流黏性比。
2.1网格划分
网格采用CH结构网格,如图1所示。总网格量控制在7×104左右,第一层网格厚度控制在弦长的1×10-5,保证y+<1,可以满足不同湍流模型的计算要求。
2.2气动特性分析
为了便于更好地与实验值进行对比,计算攻角采用文献[9]给出的角度,分别选取-4.07°,-1.98°,-0.4°,0.94°,2.6°,4.08°,5.69°,7.08°,8.62°,10.2°,11.69°。S-A_MTV入口条件的湍流修正黏度取0.001 m2·s-1,S-A_TVR入口条件的黏性系数比为10。其余湍流模型的入口出口湍流边界条件,均采用湍流强度为3.5%,湍流黏性系数比为3,计算结果如图2和图3所示。

图1SD7032翼型网格Fig.1Grid of SD7032 airfoil
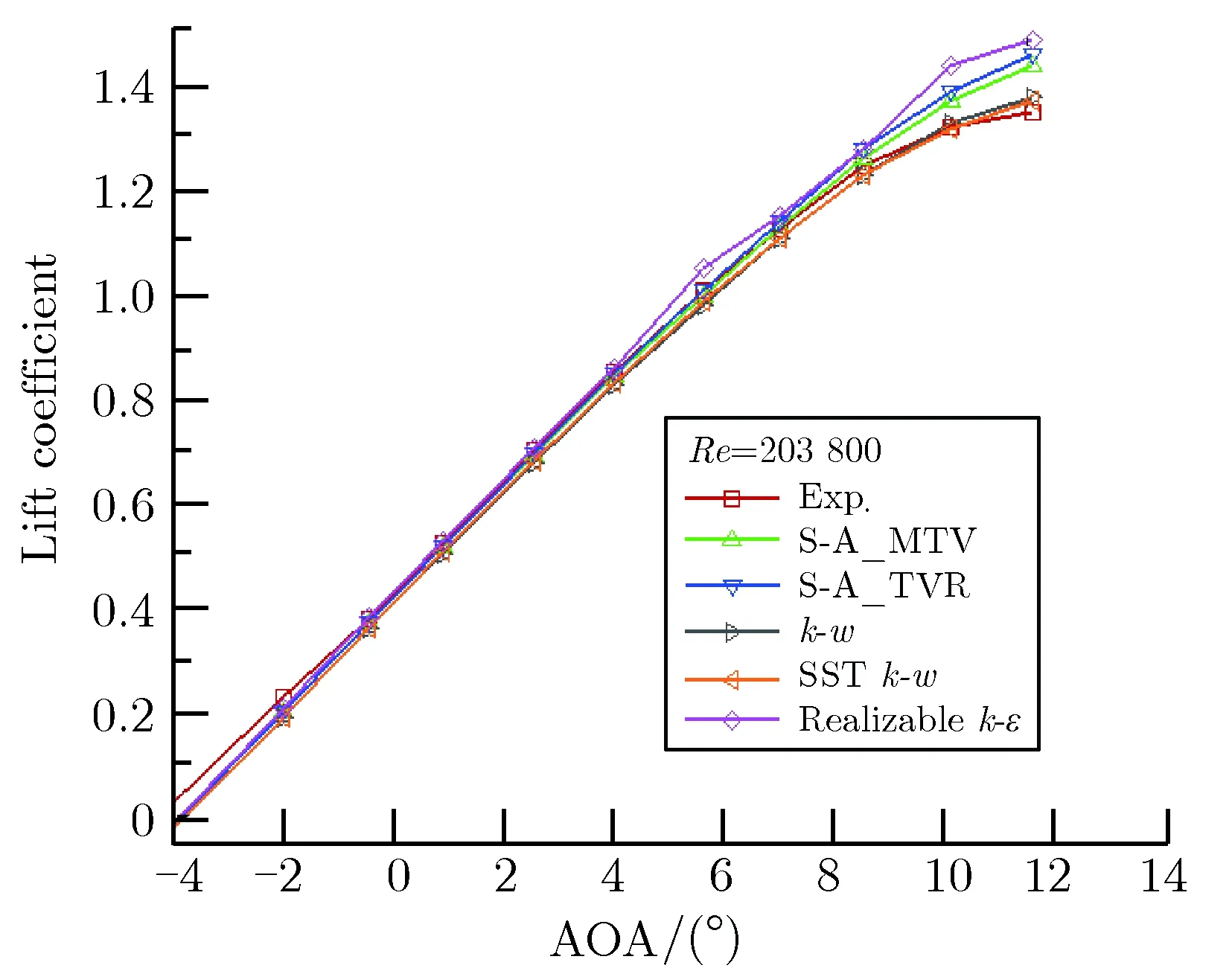
图2升力系数对比图Fig.2Comparison of different lift coefficients
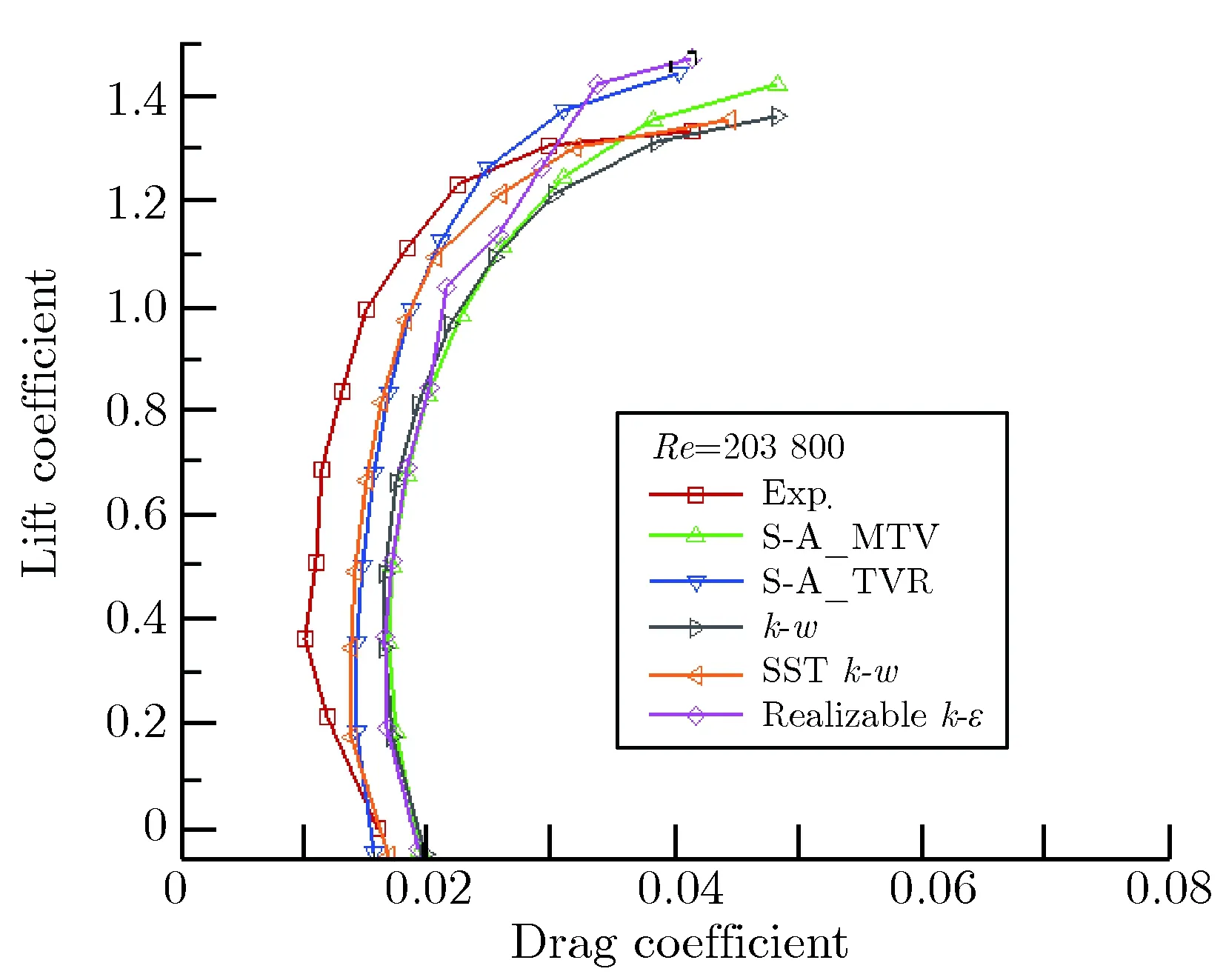
图3极曲线对比图Fig.3Comparison of polar curves
从图2可以看出,不同的湍流模型都能较好地预测升力系数,图3显示不同湍流模型对阻力系数的预测差异较大。对于S-A模型,采用不同的边界条件阻力系数也有明显差异。当攻角大于8°时,不同的湍流模型计算的升力系数差异较明显。对于S-A模型来说,采用不同的边界条件,阻力系数的预测差异也很明显,在攻角稍微大时,不同的湍流模型计算升阻系数的差异更明显。通过对比可以看出,S-A_MTV和SSTk-w计算结果与实验值比较接近,都能够较好预测升阻系数。直接采用transition SST模型计算的收敛曲线,一直无法收敛,出现了较大波动,特别是阻力系数的收敛曲线波动较大。如图4所示。

(a) Convergence of lift coefficient
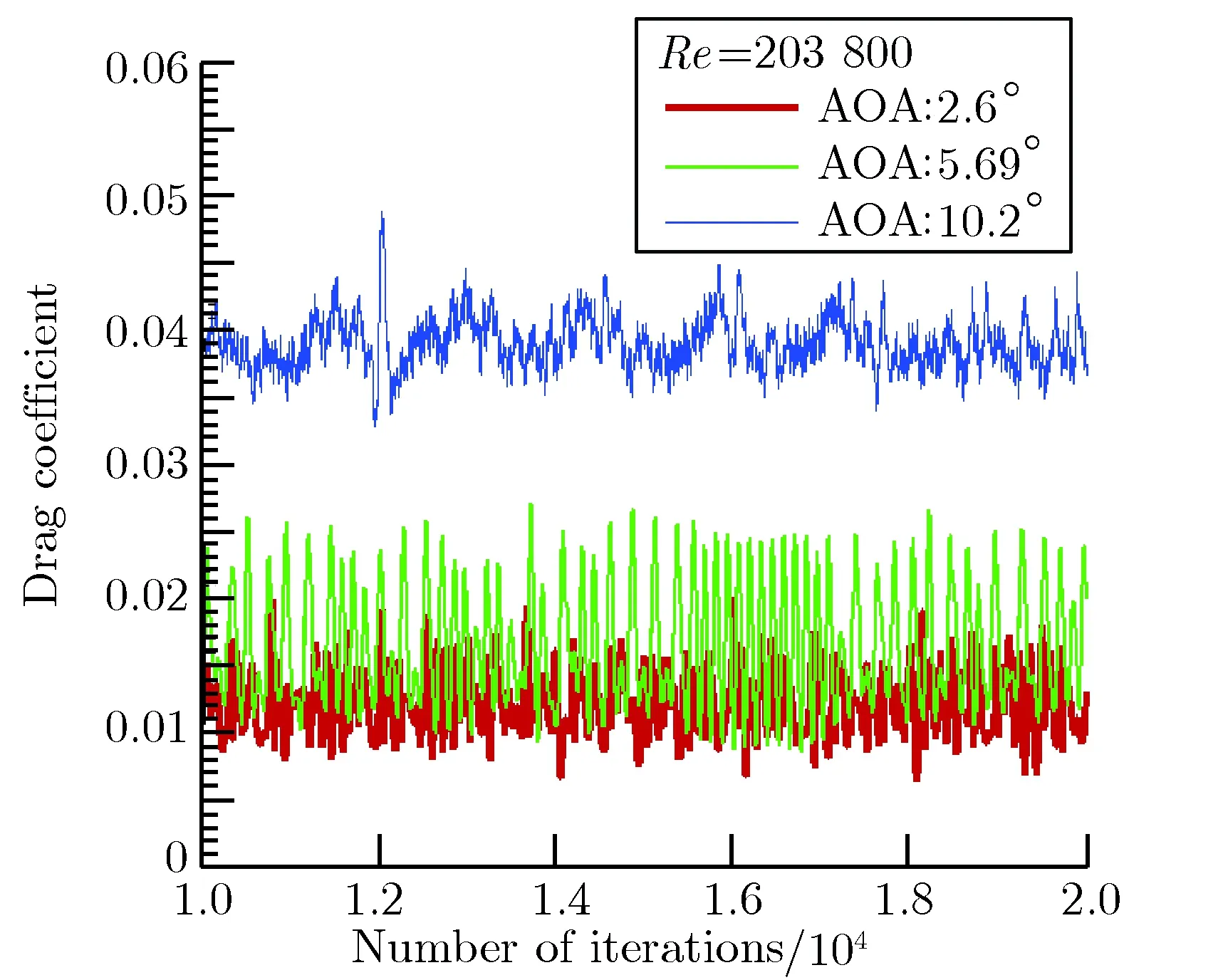
(b) Convergence of drag coefficient图4升力和阻力系数收敛曲线Fig.4Convergence curves of lift and drag coefficients
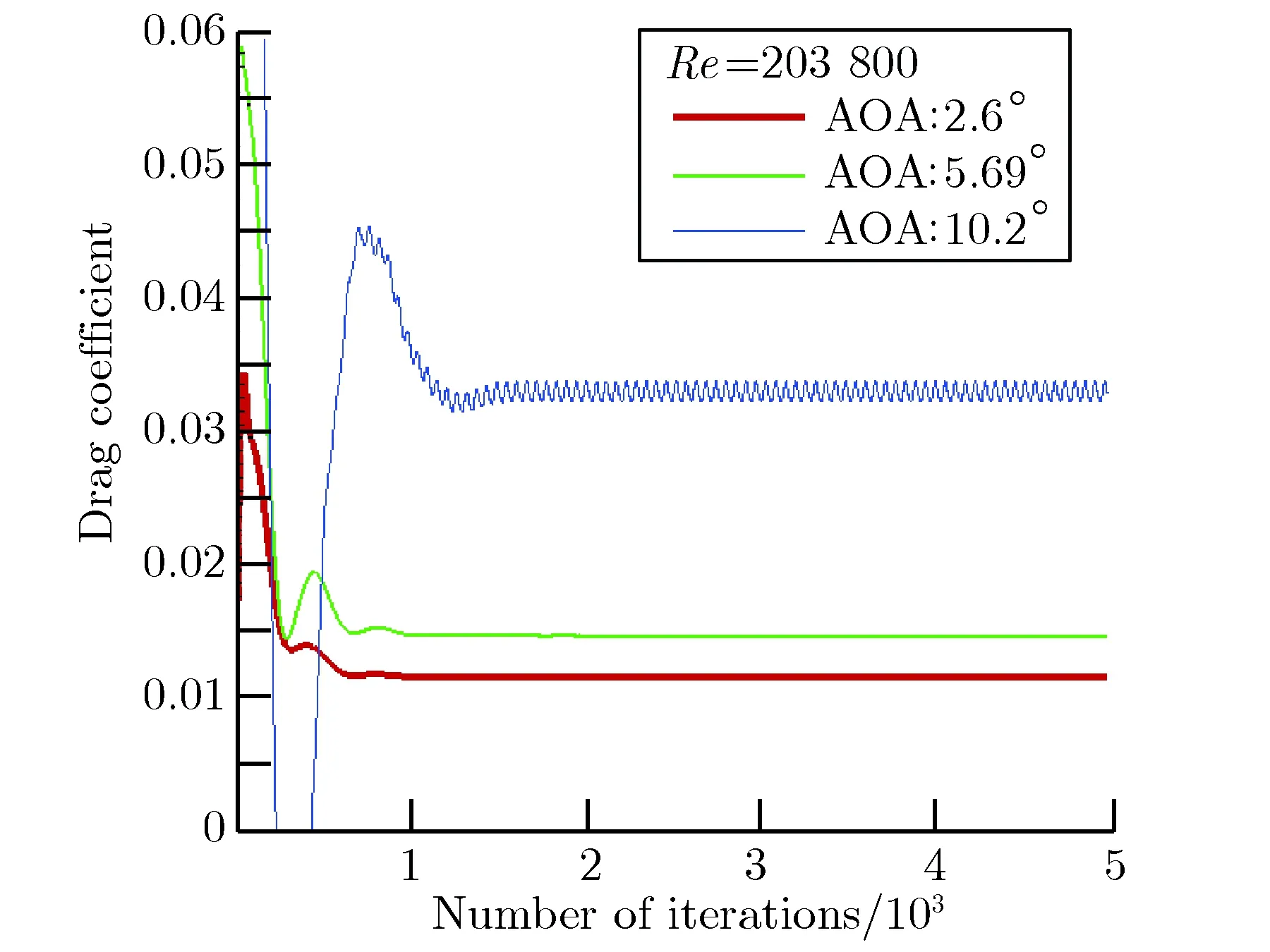
出现图4所示现象的原因可能是由于transition SST模型预测的转捩区流动产生了较大的不稳定涡,且该模型对转捩动量厚度雷诺数计算不恰当所致。根据本文的方法对transition SST模型进行改进,通过编写udf(user-defined function)控制转捩,可以得到一个稳定的收敛值,且该值与实验值更加接近,流动收敛性和稳定性都有了较大改进。结果如图5所示。
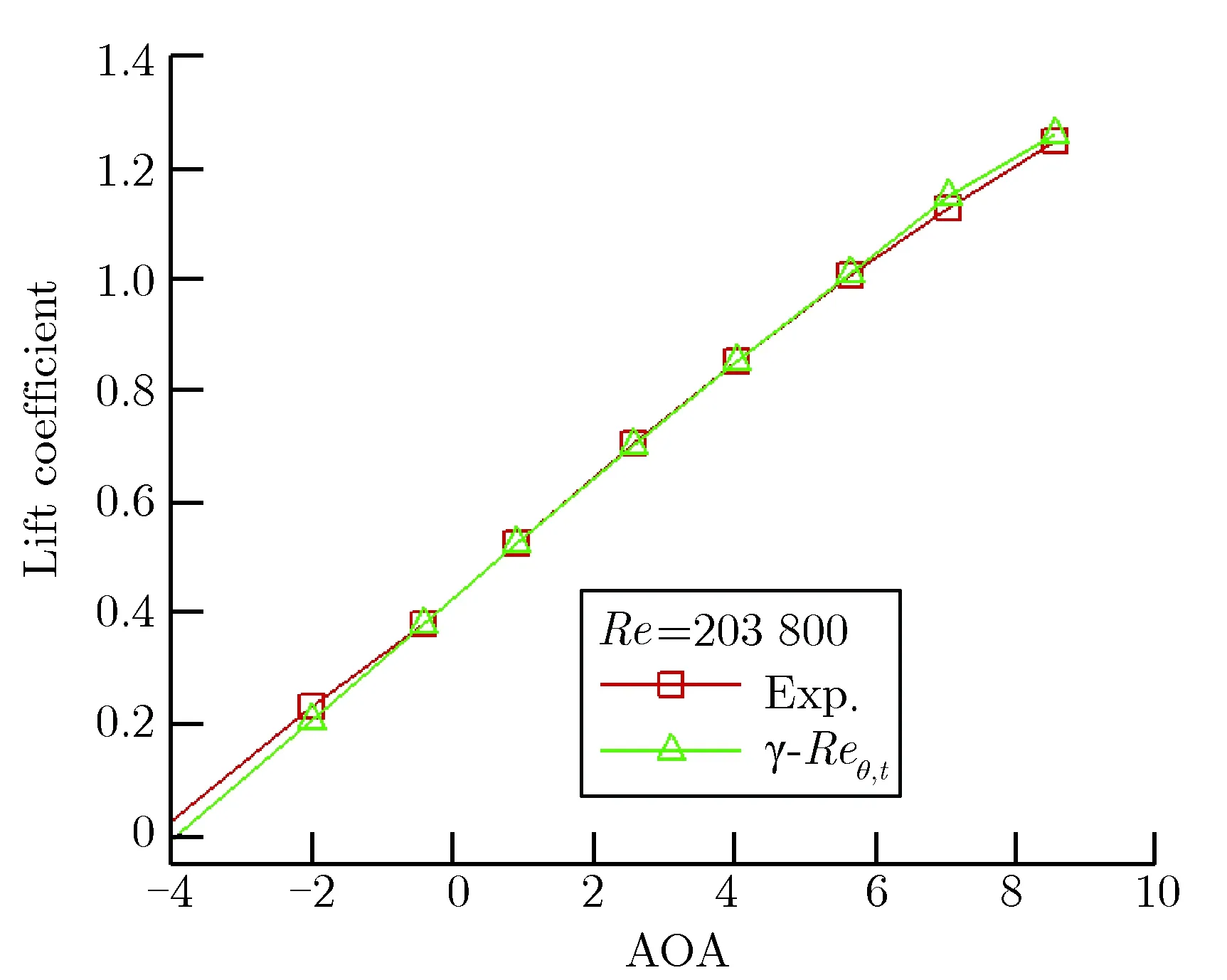
从图5可以看出,通过修正γ-Reθ,t转捩模型后,升力系数和阻力系数在小攻角下能够得到稳定值,并且收敛速度有了较大提升,在大攻角时虽然也有一定的波动,但只是在一定值附近做周期性小振幅振荡。图6给出了小攻角范围内,采用改进的γ-Reθ,t转捩模型计算的气动力参数。
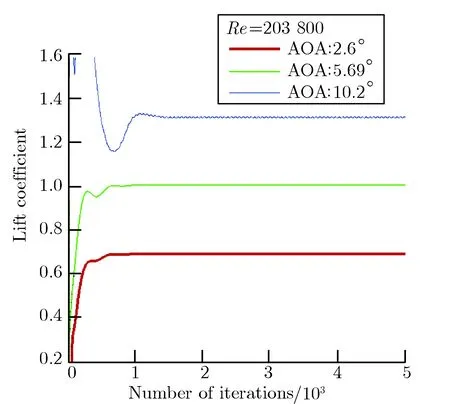
(a) Modified convergence of lift coefficient
(b) Modified convergence of drag coefficient
图5改进后的升阻系数收敛曲线
Fig.5Modified convergences of lift and drag coefficients
(a) Lift coefficient calculated by γ-Reθ,ttransition model

(b) Polar curves calculated by γ-Reθ,ttransition model
图6采用γ-Reθ,t转捩模型计算得到的升力参数及极曲线
Fig.6Lift coefficient and polar curves calculated by modified γ-Reθ,ttransition model
从图6可以看出,采用γ-Reθ,t转捩模型计算得到升力系数和极曲线都与实验值非常吻合,特别是0°~6°的攻角范围内,曲线几近重合。计算结果表明:采用转捩模型计算的阻力系数比采用全湍流模型计算的阻力系数要低,更接近实验值。因此,采用γ-Reθ,t转捩模型计算低雷诺数的升阻特性,能够得到更加准确的结果。
图7给出了transition SST模型和改进的γ-Reθ,t模型计算压力云图, 对比转捩模型计算的压力云图可以看出,采用改进的γ-Reθ,t转捩模型,流过翼型表面的不稳定降低,在翼型后缘没有明显的不稳定涡形成,更加符合低雷诺数翼型的实际流动。
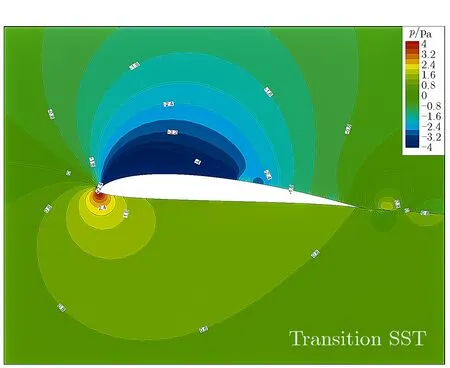
(a) Pressure coutour calculated by transition SST model

(b) Pressure coutour calculated by γ-Reθ,t transition model图7Transition SST模型和改进的γ-Reθ,t转捩模型 计算的压力云图对比Fig.7Comparison of pressure coutour calculated by transition SST and modified γ-Reθ,t transition models
3结论
不同的湍流模型和转捩模型都能较准确地估计升力系数的大小,但是对阻力系数, 计算差异较大。对于低雷诺数流动,不考虑转捩时,采用SSTk-w湍流模型能够得到与实验值比较接近的结果。考虑转捩时,采用本文提出的改进γ-Reθ,t转捩模型,与原始transition SST转捩模型比较,本文方法容易理解,求解过程简单,对湍流度等参数的敏感性降低,且能够得到更加接近实验的计算结果,适合工程上应用。本文方法具有较好的灵活性,可根据不同应用范围求出相应的参数,同时也可以作为对transition SST模型的一种对比和验证。但该方法是否适用于更大范围的流动还需进一步验证。
[1]周欣, 杨爱民, 翁培奋. 低雷诺数下翼型粘性绕流主动流动控制的数值模拟[J]. 上海大学学报: 自然科学版, 2007,13(2): 193-196.(ZHOU Xin, YANG Ai-min,WENG Pei-fen. Simulation of active flow control on viscous flow around airfoil under low Reynolds number[J]. Journal of Shanghai University: Natural Science, 2007, 13(2): 193-196.)
[2]FENNINGER W P, VEMURU C S. Design of low Reynolds number airfoils [J]. Journal of Aircraft,1990,27(3): 204-210.
[3]刘沛清, 马利川, 屈秋林, 等. 低雷诺数下翼型层流分离泡及吹吸气控制数值研究[J]. 空气动力学学报, 2013, 31(4): 518-524. (LIU Pei-qing, MA Li-chuan, QU Qiu-lin, et al. Numerical investigation of the laminar separation bubble control by blowing/suction on an airfoil at lowRenumber[J]. Acta Aerodynamica Sinica, 2013, 31(4): 518-524.
[4]MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables-Part I: model formulation[J]. ASME Journal of Turbomachinery, 2006, 128(3): 413-422.
[5]MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables-Part II: test cases and industrial applications[J]. ASME Journal of Turbomachinery, 2006,128(3): 423-434.
[6]LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2 894-2 906.
[7]TOMAC M, PETTERSSON K, RIZZI A. Calibration and verification of aγ-Reθ,ttransition prediction method for airfoil computations[C]//51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, AIAA 2013-0407, 2013.
[8]MICHEL R. Determination du point de transition et calcul de la trainee des profiles dailes en incompressible[R]. ONERA Report 1/1578A, 1951.
[9]SELIG M S, GUGLIELMO J J, BROEREN A P, et al. Summary of Low-Speed Airfoil Data[M]. Virginia: Soar Tech Publications, 1995: 211-213, 286.
Research on Turbulent Models at the Low Reynolds Number Flow
CHEN Li-li,GUO Zheng
(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha410073,China)
Numerical simulation of the flow over SD7032 airfoil was performed using the RANS method by solving the Navier-Stokes(N-S)equations with six turbulence modelsoperating at the low Reynolds number of 203 800. The lift and drag coefficients and convergences of six turbulence models at the low Reynolds number flow were evaluated. The results showed that when taking no consideration of flow transition, the lift and drag coefficients calculated by SSTk-wmodel could be approximated by the experimental value. However, when taking flow transition into consideration, stability and convergence performances of modified γ-Reθ,ttransition model got significantly improved, the calculation results agreed with the experimental values within a small attack angle.
low Reynolds number flow;SD7032 airfoil;turbulent models;γ-Reθ,ttransition model
2016-01-15;
2016-04-12 †通信
郭正(1974- ),男,河北辛集人,教授,博士,主要从事计算流体力学及飞行器气动设计研究。
E-mail:guozheng@nudt.edu.cn
V211.3
A
2095-6223(2016)031001(5)

