基于直流X射线连续能谱的平晶摇摆曲线测量方法

马戈,唐波,3，黑东炜，魏福利，周海生，罗剑辉，李斌康,夏惊涛

(1.西北核技术研究所，西安710024；2.强脉冲辐射环境模拟与效应国家重点实验室，西安710024；3.清华大学工程物理系，北京100084)



基于直流X射线连续能谱的平晶摇摆曲线测量方法

马戈1,2,唐波1,2,3，黑东炜1,2，魏福利1,2，周海生1,2，罗剑辉1,2，李斌康1,夏惊涛1,2

(1.西北核技术研究所，西安710024；2.强脉冲辐射环境模拟与效应国家重点实验室，西安710024；3.清华大学工程物理系，北京100084)

采用直流X射线连续能谱照射晶体，以极小的步进角，测量一定角度范围内，不同入射角度下的衍射能谱，通过提取各个角度衍射能谱中同一能量X射线的衍射强度，微分得到该能量的平晶摇摆曲线。与传统测量方法相比，该方法具有更大的X射线能量测量范围，可通过一次角度扫描，同时给出多个能量的摇摆曲线。利用该方法开展了16～21 keV区间内LiF(200)平晶摇摆曲线的相对强度标定，结果表明，晶体摇摆曲线的半高宽随X射线能量增加而缓慢减小，而峰值强度随X射线能量增加则缓慢增加，在入射能谱强度变化较大区间内，该方法测量结果的不确定度较大。

摇摆曲线；衍射能谱；相对强度；连续谱X射线

在脉冲X射线能谱测量领域，晶体分光法是非常重要的一种测量手段，利用晶体对X射线的衍射，将X射线能谱转换为衍射强度的空间分布，再根据不同能量的积分衍射效率反推原始能谱。积分衍射效率是X射线能谱测量过程中非常重要的参数，直接反映入射X射线与衍射X射线的强度关系，其数值由晶体摇摆曲线积分得到。通常，采用理论计算并结合部分能点的晶体摇摆曲线标定，积分得到积分衍射效率。经过数十年的发展，已建立了一些理论[1-2]，并计算得到了不同材质和结构下的晶体摇摆曲线[3-4]。但由于摇摆曲线受晶体内部微结构和缺陷的影响难以精确计算，因此，在理论计算的基础上，还需要开展摇摆曲线的实验标定工作。

现有的晶体摇摆曲线标定方法，大多基于同步辐射和衍射仪的单色化X射线展开，存在诸多问题，如在同步辐射装置上，利用双晶单色器[5-6]可以实现十几千电子伏以下连续可调的单色X射线输出，但能谱范围窄，且机时非常紧张，申请困难；利用直流X射线源阳极靶特征X射线[7-9]，或采用Ross滤片对[10]可以实现几千电子伏以上多个近似单色X射线输出，但单色性相对较差，实际可测量的能点非常少。

为了获得更多能点下的晶体摇摆曲线，本文主要基于直流X射线源和高纯锗探测器，研究十几至几十千电子伏能量范围内X射线平晶摇摆曲线的测量方法。

1测量原理

如果一束能量为E，强度为Iin的X射线以角度θ入射晶面，则在衍射方向上，衍射X射线的强度Idiff可以表示为

(1)

其中，P(E,θ)表示能量为E的X射线在θ角时衍射强度和入射强度的比值。P(E,θ)随角度θ的变化关系即为该晶面对能量E的摇摆曲线。可通过对摇摆曲线的积分得到积分衍射效率Rc：

(2)

其中，θ1和θ2分别表示X射线入射晶面的角度极小值和极大值。当入射X射线具有一定能量范围[E,E+ΔE]，且入射晶面的角度存在一定的发散[θ,θ+Δθ]时，在衍射方向上接收到的衍射X射线强度可表示为

(3)

考虑一束具有一系列不同能量的X射线以多个角度入射晶体。令X射线能量为{E1,E2,…,Em}，入射角度为{θ1,θ2,…,θn}，探测器能量分辨间隔为ΔE，入射X射线发散角为Δθ，分别对各个能量在不同角度下的衍射X射线强度进行测量，可将测量结果整理为矩阵形式：

(4)

其中，第i行元素表示同一角度θi下不同能量X射线的衍射强度，即衍射能谱；而第j列元素表示同一能量Ej的X射线在不同角度入射时的衍射强度。若忽略不同角度入射时X射线的强度变化，则有

(5)

因此，要获得能量为Ej的X射线的摇摆曲线，只需在其对应的布拉格角附近，以一定的角度间隔测量多个角度下的衍射能谱，并提取各个能谱中Ej的强度信息即可。

2实验过程

基于Unique II型荧光分析仪和高纯锗探测器，开展晶体摇摆曲线的实验测量工作。实验装置如图1所示，实验参数如表1所列。

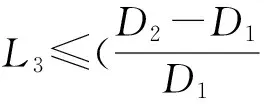
实验测量过程和衍射仪上的晶体摇摆曲线标定过程一致，只需在选定的测量角度范围内，根据设置好的测量角度间隔，逐个角度测量晶体衍射能谱即可。图2为测量得到的部分入射角度下的衍射能谱。

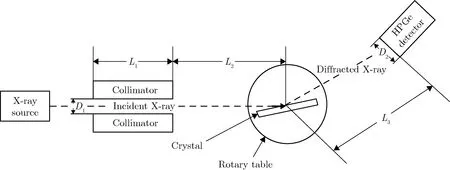
图1晶体摇摆曲线测量装置示意图Fig.1Sketch of the rocking curve measurement system 表1晶体摇摆曲线标定实验参数 Tab.1Parameters used in rocking curve calibration

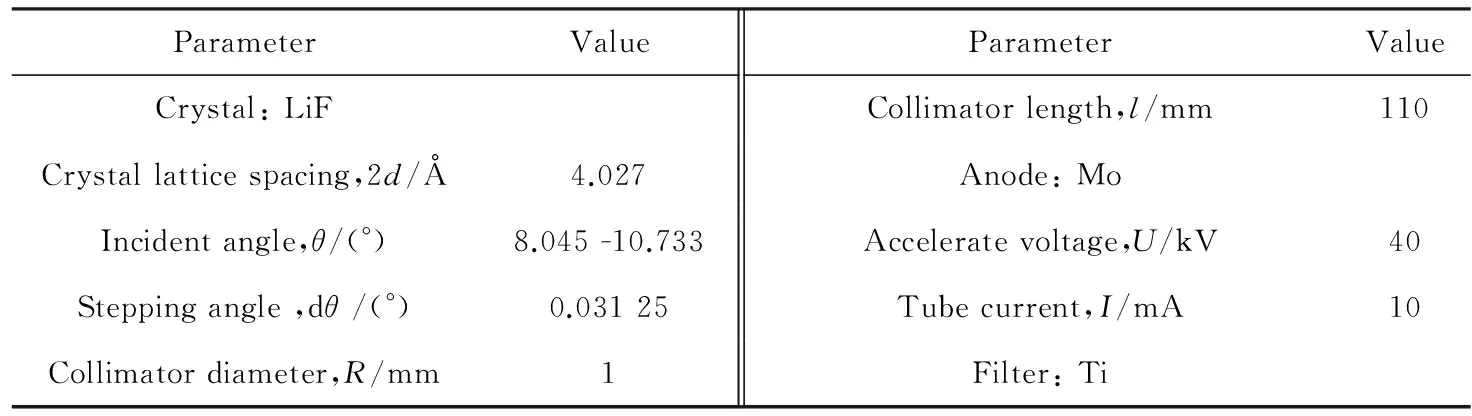
ParameterValueParameterValueCrystal:LiFCollimatorlength,l/mm110Crystallatticespacing,2d/Å4.027Anode:MoIncidentangle,θ/(°)8.045-10.733Acceleratevoltage,U/kV40Steppingangle,dθ/(°)0.03125Tubecurrent,I/mA10Collimatordiameter,R/mm1Filter:Ti

(a)θ=8.826°

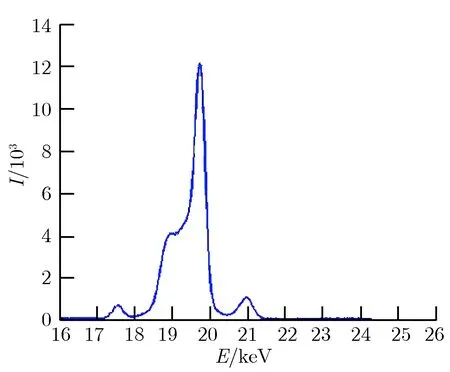
(b)θ=9.233°

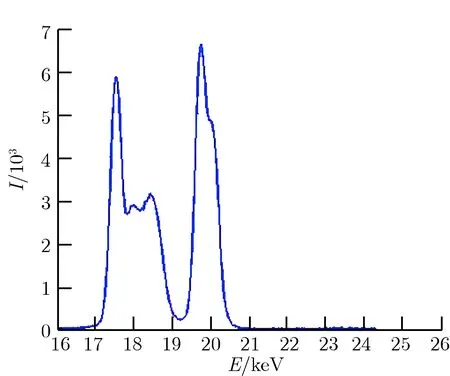
(c)θ=9.733°

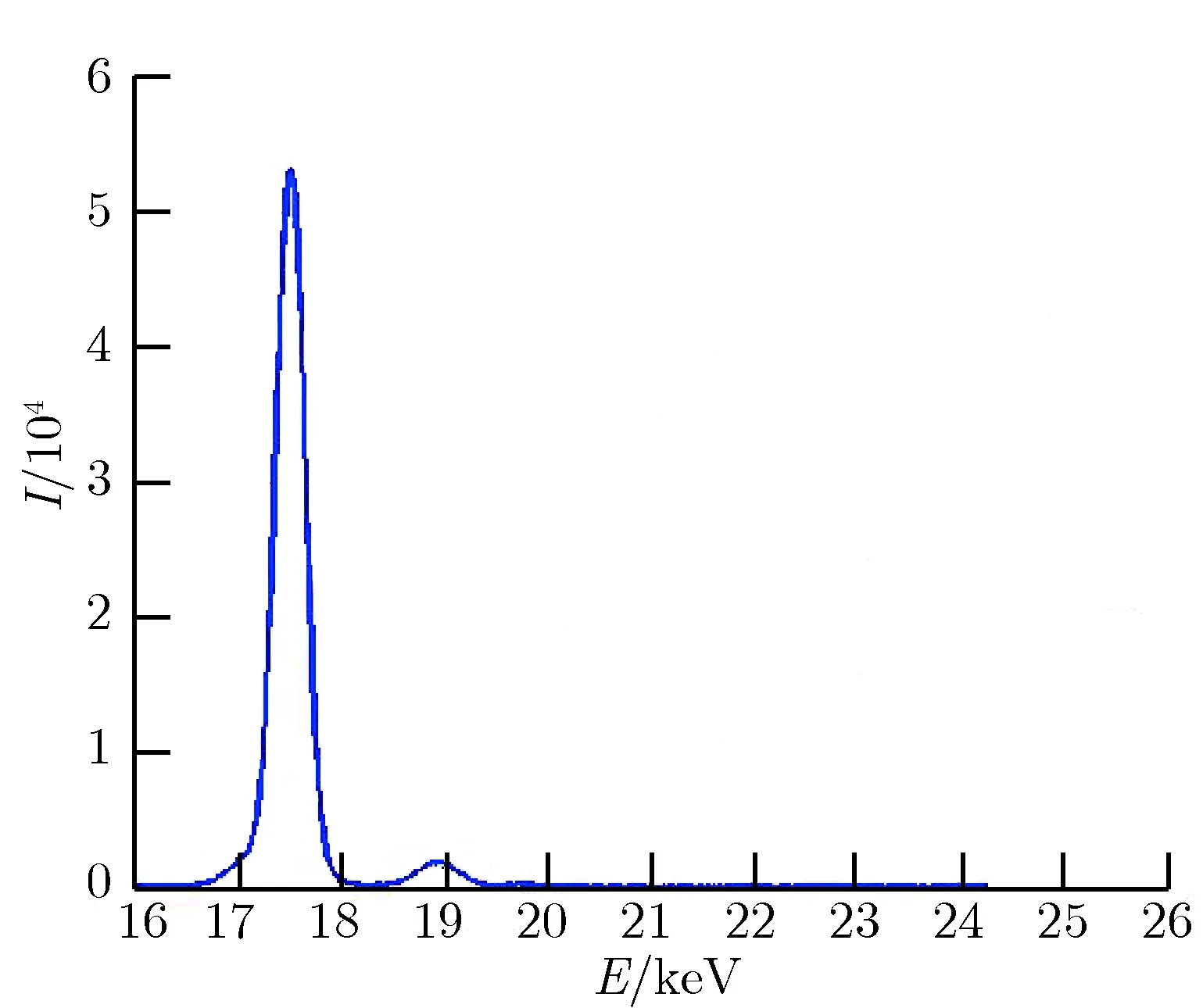
(d)θ=10.170°

图2部分入射角度下的晶体衍射能谱

Fig.2Diffraction spectra at different incident angles

3结果与分析

选取18.56 keV及18.95 keV两个能点，分别提取各个衍射能谱中这两个能量下的衍射强度，可以得到衍射强度与入射角度之间的变化关系，如图3所示。由式(3)可知，当ΔE和Δθ都趋近于0时，衍射强度随入射角度的变化曲线即为该能量对应的摇摆曲线；而该条件不满足时，测量得到的衍射强度随入射角度的变化曲线，反映的是摇摆曲线在不同角度区间积分强度的变化。当Δθ大于摇摆曲线角宽度时，通过对衍射强度随入射角度的变化曲线求微分，即可得到摇摆曲线。在实验中，Δθ约为0.52°，与预计的摇摆曲线角宽度处于同一量级，因此，图3中的衍射强度随入射角度的变化曲线在经过峰分离后，还需要进行微分处理，才能得到实际的摇摆曲线。

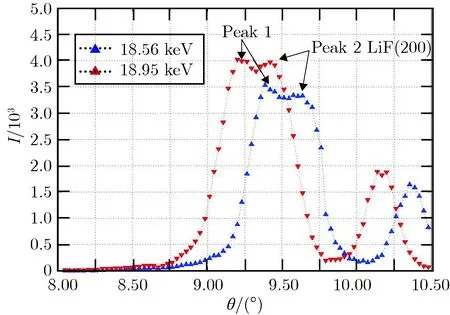
图3衍射强度与晶体入射角度的变化关系Fig.3Diffraction intensity vs. incident angle

为比较不同能量对应的摇摆曲线形态差异，根据积分强度对测量得到的摇摆曲线进行了归一化。图4为LiF(200)晶体的摇摆曲线，横坐标ΔθB表示入射角与该能量布拉格角的角度差，纵坐标表示归一化衍射强度。

(a)E=18.56 keV

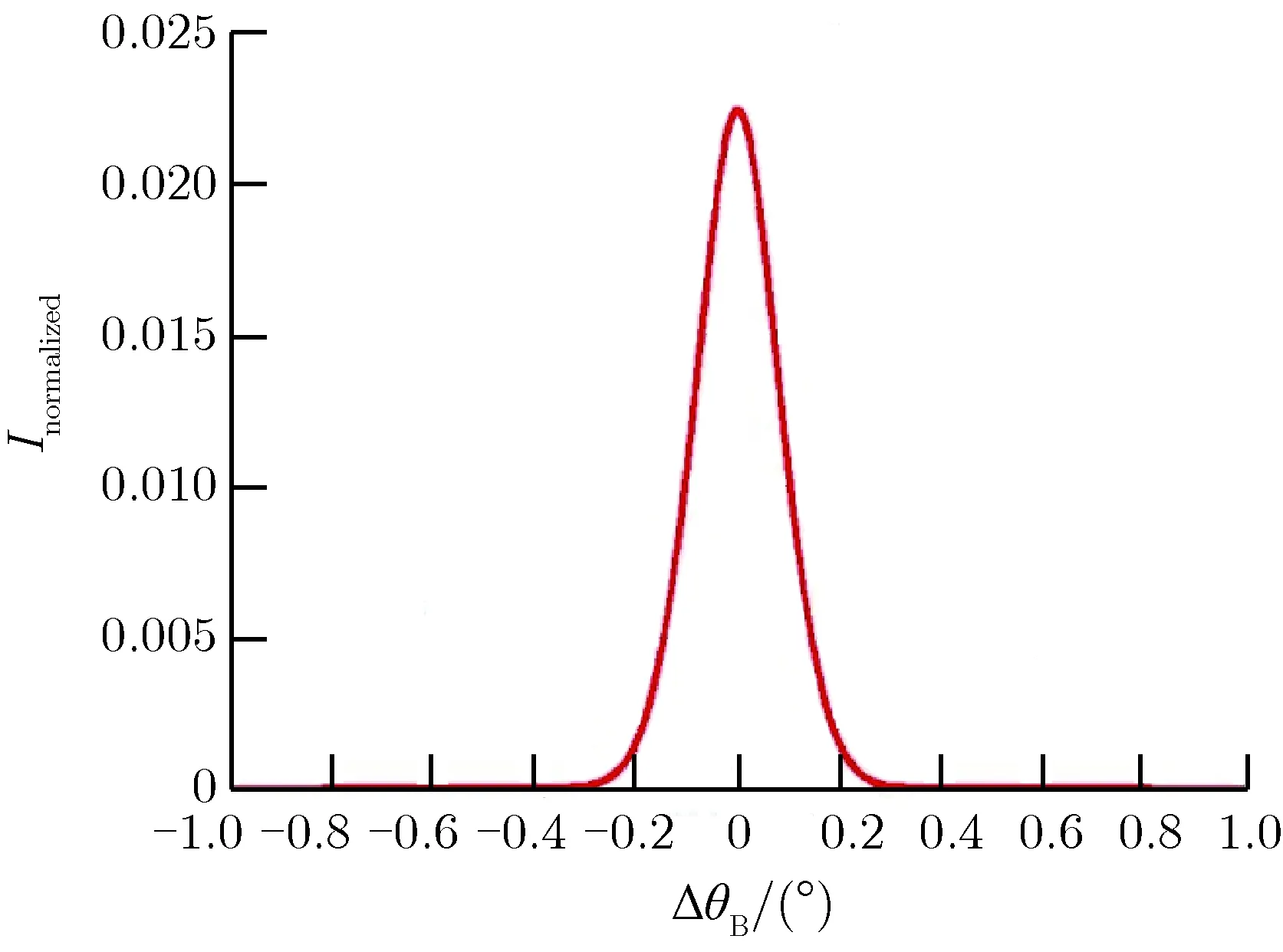
(b)E=18.95 keV图4LiF(200)晶体的摇摆曲线Fig.4X-ray rocking curve of LiF(200)

由图4可知，两条曲线形态相近，与文献[5,7]中测量得到的摇摆曲线形态也相近，均接近高斯分布，但由于入射X射线能量的差异，本文实验得到的摇摆曲线峰值强度及半高宽与文献[5,7]中的相应数据存在较大不同。图4中18.56 keV对应曲线的半高宽为0.196°，峰值强度为2.092×10-2，18.95 keV对应摇摆曲线半高宽0.190°，峰值强度为2.236×10-2。两条摇摆曲线的半高宽基本相同，但18.95 keV下的峰值强度较18.56 keV下的相应值增大约6.88%。

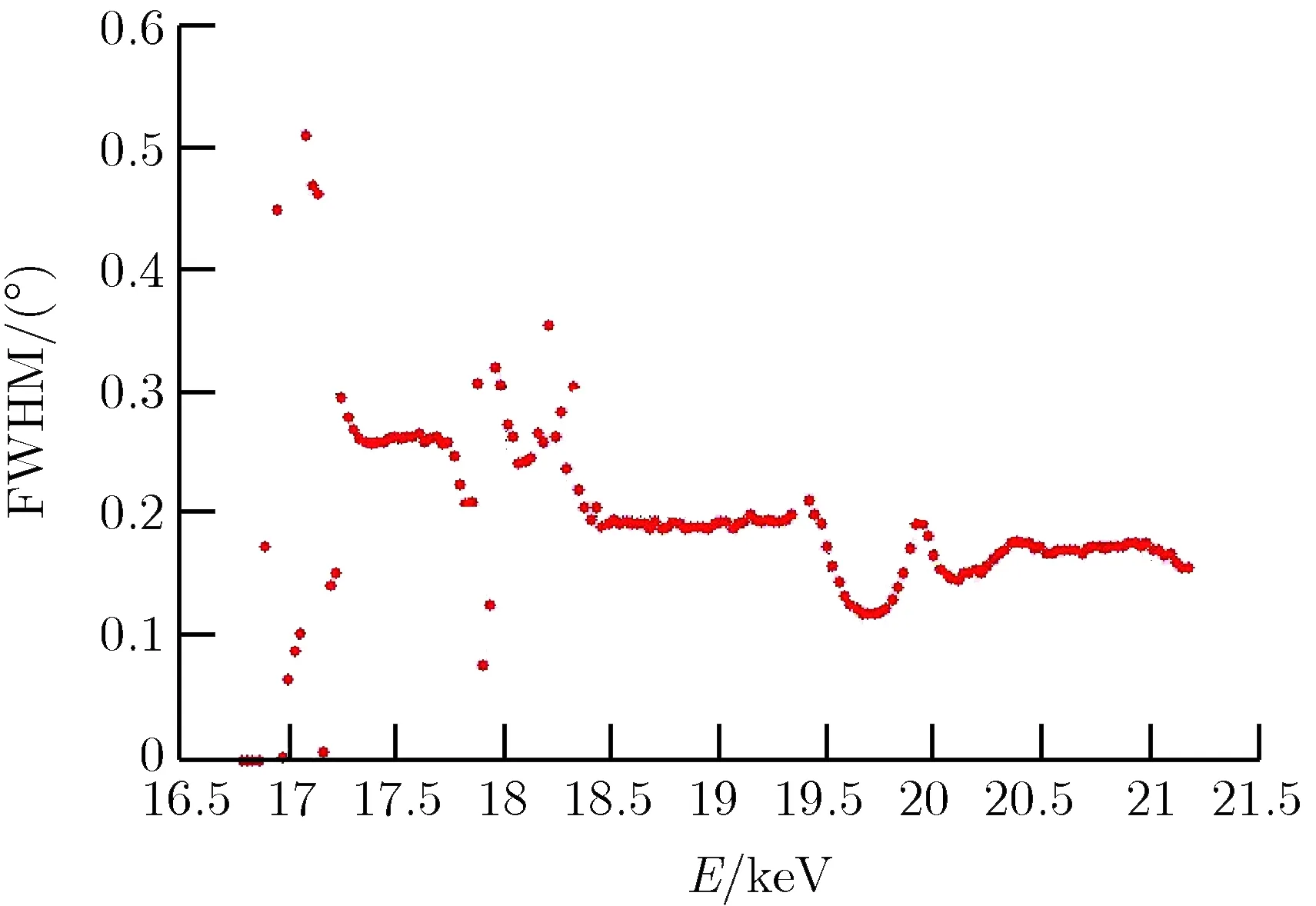
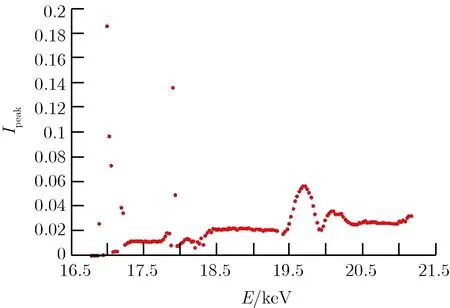
图5为LiF(200)晶体在16～21 keV能量区间内的摇摆曲线半高宽和峰值强度随X射线能量的变化关系。

(a)FWHM

(b)X-ray energy图5LiF(200)的摇摆曲线半高宽及峰值强度 随入射X射线能量的变化Fig.5FWHM and peak intensity of LiF(200) rocking curve vs. incident X-ray energy

由图5可知，总体上，随着X射线能量的上升，摇摆曲线的半高宽逐渐减小，而峰值强度逐渐增大，这与理论推导得到的变化趋势基本符合[5]；但是，在特征X射线能量及18 keV附近，测量得到的摇摆曲线形态存在较大的跳变。分析认为，产生跳变的主要原因一方面是在特征X射线能量附近，能谱强度存在极大的变化，而实验中采用的光路设计主要针对入射强度较弱的X射线，当入射强度过高时，探测器测量得到的能谱形态，会由于过大的死时间及较多的复合计数产生较大的不确定度。本实验中，在特征X射线能量的±0.25 keV能量区间内，测量的摇摆曲线不可信；另一方面，在对衍射强度随入射角度的变化曲线进行峰分离时，由于18 keV附近的两峰过于接近，分离得到的衍射峰形态与实际形态存在较大偏差。对此，在峰分离时，可以考虑将临近能量的峰分离结果作为基函数进行峰分离，并通过检查分离结果的标准偏差，判断结果是否可用。

在对18.56 keV和18.95 keV能量下摇摆曲线峰值强度的测量中，射线源强度的相对不确定度为0.5%，高纯锗探测器计数测量的相对不确定度为0.2%，旋转台定位的相对不确定度为0.02%，拟合峰值强度的相对不确定度为4%，峰值位置的相对不确定度为0.1%，总相对测量不确定度约为4%。

4结论

基于直流X射线源连续能谱，开展了晶体摇摆曲线标定研究，实现了对LiF(200)晶体16～21 keV能量区间内连续能量的晶体摇摆曲线测量，给出了摇摆曲线半高宽及峰值强度随X射线能量的变化趋势，证明了测量方法的可行性，这对实现硬X射线晶体衍射能谱的反演计算具有重要意义。但是，受实验条件限制，摇摆曲线无法直接测量，需要通过数据处理间接得到，因而引入了较大不确定度。下一步还需要优化实验条件及数据处理方法，以便提高测量精度，降低处理过程引入的不确定度。

[1]ANDRE A. Dynamical Theory of X-Ray Diffraction[M]. Oxford: Oxford University Press, 2000.

[2]HENKE B L, GULLIKSON E M, DAVIS J C. X-ray interactions: Photoabsorption, scattering, transmission, and reflection atE=50-30 000 eV,Z=1-92[J]. Atomic Data and Nuclear Data Table, 1993, 54(2): 181-342.

[3]丁国庆. X射线双晶衍射测试曲线的计算机模拟分析[J]. 半导体技术, 1998, 23(6): 50-54.(DING Guo-qing. Analysis of double crystal X-Ray diffraction by computer-modelling[J]. Semiconductor Technology, 1998, 23(6): 50-54.)

(下转第030801-7页)

Measurement of Rocking Curve of Flat Crystal with Continuous X-ray Spectrum

MA Ge1,2,TANG Bo1,2,3,HEI Dong-wei1,2,WEI Fu-li1,2,ZHOU Hai-sheng1,2,LUO Jian-hui1,2,LI Bin-kang1,XIA Jing-tao1,2

(1.Northwest Institute of Nuclear Technology，Xi’an710024,China;2.State Key Laboratory of Intense Pulsed Radiation Simulation and Effect，Xi’an710024,China;3.Department of Engineering Physics，Tsinghua University，Beijing100084，China)

A new measurement method of X-ray diffraction rocking curve was proposed. Flat crystal was irradiated by continuous X-ray at different incident angles, and energy spectra of diffracted X-ray were measured for every incident angle. X-ray diffraction rocking curves of different X-ray energy could be calculated upon diffraction intensity curves which were summarized from energy spectra of diffracted X-ray. In comparison with other rocking curve measurements, this measurement method had a wider measuring range in X-ray spectrum. Several rocking curves could be measured during one incident angle scanning. This measurement method was used to measure the rocking curves of LiF(200) in the energy range of 16 keV to 21 keV. The results showed that, with the increase of X-ray energy, the FWHM of rocking curves decreased, while the peak intensity increased. The disadvantage of this measurement method was that the relative uncertainties of the data measured in the energy range where the intensity of incident X-ray changed rapidly could be very large.

rocking curve;diffraction spectra;relative intensity;continuous X-ray

2016-05-03；

2016-06-06

马戈(1985- )，男，回族，浙江宁波人，助理研究员，学士，主要从事X射线诊断技术研究。

E-mail:mage@nint.ac.cn

TL99

A

2095-6223(2016)030201(5)