基于高斯伪谱法优化算法的火星气动刹车轨道仿真

黄峰，黄悦琛，李海阳

(国防科技大学长沙410073)



基于高斯伪谱法优化算法的火星气动刹车轨道仿真

黄峰，黄悦琛，李海阳†

(国防科技大学长沙410073)

以未来火星探测任务为背景，简要分析了通过气动刹车到达目标轨道方案的优缺点。基于给定的火星大气修正指数模型，建立了气动刹车的动力学模型。针对飞行器自身和轨道限制，设置必要的约束条件，利用高斯伪谱法求解出气动刹车方案中每个周期所需的维持近火点高度的脉冲速度增量，实现了通过气动刹车的方式到达指定轨道的目标。结果表明，利用高斯伪谱法优化计算得到的气动刹车方案可以满足要求，可为气动刹车相关的后续研究提供新的思路。

火星探测；高斯伪谱法；轨道仿真；气动刹车

aerobraking

开展火星探测对于人类探索地球起源具有重要意义[1]，美国国家航空航天局(National Aeronautics and Space Administration, NASA)和欧洲宇航局(European Space Agency, ESA)等世界主要航天机构都对火星探测提出了一系列构想。在飞抵火星及到达目标轨道的过程中，燃耗的降低会使飞船的机动性减小，从而引起总时间消耗增多。因此，需要根据飞船的运载能力和任务时间的要求对时间和燃料进行优化设计，使二者的综合性能指标满足探测任务的要求，在降低燃耗的同时使时间消耗也能满足时间要求。气动刹车方案对节省燃料有着显著效果，虽然其时间消耗略长，但对非载人探索任务而言，增加时间通常是可以接受的，且该方案已被多次应用。历史上NASA曾4次成功地采取气动刹车方案实现轨道转移，即“麦哲伦”(Magellan)号飞船[2]的金星探测任务，“火星全球测量者”(Mars global surveyor, MGS)号[3]、“奥德赛”(Odyssey号[4])和“火星勘测轨道飞行器”(Mars reconnaissance orbiter, MRO)[5]的火星探索任务等。

为了实现气动刹车准确入轨，并满足时间和燃料消耗的性能指标，需要根据目标天体的大气环境以及到达火星影响球的初始条件，优化计算在火星环绕轨道的发动机所需提供的冲量。历史上成功使用气动刹车的案例仅有4个，且对每个周期内，飞行器所需发动机提供维持近火点高度的速度增量方式，鲜有报道，因此，本文基于高斯伪谱法优化算法(Gauss pseudospectral optimization software，GPOPS)，结合历史上成功案例的技术参数，提出了一种新的计算控制量，即发动机提供的冲量，可为不同类型的火星探测飞行器提供一种新的轨道转移选择模式。

1气动刹车流程及其数学模型

1.1气动刹车流程简介

气动刹车是指借助大气阻力减速并利用主动机动实现飞行器变轨的一种方式，其整个过程如图1所示。 该过程分3个阶段， 即初始环绕调整段(walk-in phase)、 主减速段(main phase)和末态脱离火星大气段(walk-out phase)。

初始环绕调整段，飞行器进入火星影响球范围，在以目标中心天体为焦点的一个大离心率的椭圆轨道上运动，并利用自身携带的设备对火星环境进行勘测，将所测数据与数据库数据进行比对修正。为保证测量精度，飞行器通常需要环绕火星飞行4～8圈，才能充分测量火星的环境参数。

当飞行器进入主减速段时，气动减速效果明显，绕火星每旋转一周都会使远火点高度逐步降低。为保证飞行器不因气动减速导致轨道高度急速下降，当飞行器每旋转一周，抵达轨道的远火点附近时，需要发动机工作进行轨道修正，以确保近火点轨道高度在合理范围内。

在末态脱离火星大气段，为了实现长时间环绕火星飞行，飞行器的环绕轨道需尽量消除大气影响，避免在每个环绕周期内多次施加机动维持轨道高度。此阶段主要依靠每个周期的单次机动，将近火点高度提高到火星大气层外，最终实现长期环绕火星飞行。

1.2火星大气模型

近火星大气密度指数模型中，将密度看作随高度分段变化的函数[6]。设高度为h，m；温度为T，℃；大气压强为p，Pa; 大气密度为ρ，(kg·m-3)；则温度T表示为

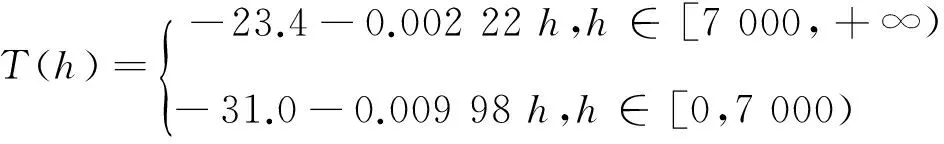
(1)

大气压强p为

p(h)=0.699×exp(-0.000 09 h)

(2)

大气密度ρ为

(3)

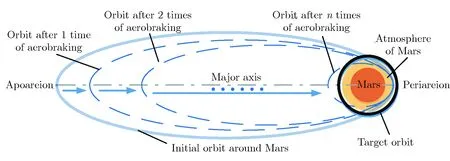
图1气动刹车过程示意图Fig.1Diagram of the process of aerobraking

该模型是NASA的格伦研发中心(Glenn Research Center)根据1996年发射的“火星全球测量者号”的观测数据建立的。尽管未考虑大气随时间变化的因素，但在概念研究中，仍可选取此模型作为切入点，继续开展工作。但是，大气密度在大于100 km的某个区间内出现强烈震荡，这与事实明显不符，原因在于:该密度模型计算的温度，在这个区间内跨越0 K，导致密度表达式的分母为0，出现了不连续现象。考虑到气动刹车过程中飞行器的防热能力有限，轨道高度过低可能会导致飞船烧毁，因此，现阶段探测任务中，轨道高度不会低于7 km，因此主要关注轨道高度在7 km以上的火星大气模型。为了解决跨越0 K引起的大气密度模型的震荡问题，需要对此模型进行适当改进。

将实际的火星大气密度看作关于高度的连续函数，进行多项式拟合，估计可以保证连续性，但会出现局部不够光滑，需要进一步优化。用一个函数替代高阶多项式，得到改进的大气密度公式为

(4)

改进的大气模型式(4)与原模型式(3)的对比结果，如图2所示。

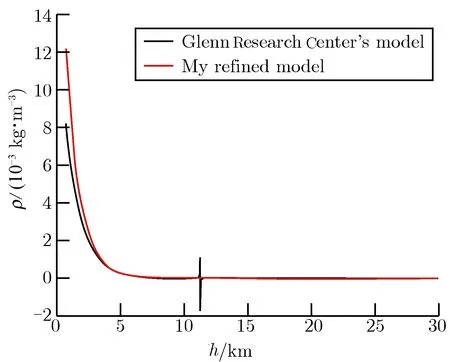
图2两种火星大气模型密度对比图Fig.2Comparison of two Mars atmosphere models

1.3动力学和运动学模型

在火星大气层内，飞行器受引力和气动力的影响。气动力分为升力和阻力，该阶段飞行器的6个状态量分别为飞行器与火星中心距离r、火心经度θ、火心纬度φ、速度V、速度倾角γ和航向角Ψ。航向角定义为正北方向与飞行器前进方向的夹角，沿顺时针转动为正。速度倾角为进入点速度方向与当地火星表面的水平面所成的夹角，当速度方向指向火星角度为负值，反之为正。在不考虑风、科里奥利力(Coriolis force)和离心力的影响时，运动方程[7-8]可由式(5)-式(8)表示：

(5)

(6)

(7)

(8)

其中，FD为阻力；FL为升力；g(r)为重力加速度；σ为倾侧角；m为飞行器质量；S为飞行器参考面积；CL和CD分别为升力系数和阻力系数；μMars为火星重力参数。

2基于高斯伪谱法的轨道优化设计

为了确保在气动刹车过程中满足进入走廊的要求，需要在远火点附近实施机动，采用脉冲方式，施加一个速度增量。

GPOPS的目标函数为

(9)

其中，Δva为在远火点施加脉冲时速度的变化量；x为6维状态向量，包含火心经度、火心纬度、与火星中心的距离、速度、速度倾角和航向角等信息。

利用优化算法求解速度冲量时，需要设置高度约束、过载约束和速度约束等。设计最低高度hmin不低于70 km，最大过载为3g(g为地球重力加速度)，飞行器速度v至少满足椭圆轨道的能量公式要求，则约束条件Φ可以表示为

(10)

3仿真分析

目前关于气动刹车的研究报道还不多，无法得到有关火星探测器所需的详尽数据，这里仅根据NASA提供的一些已成功实现气动刹车的火星探测飞船的部分基本数据，并结合有关技术手册，在理论论证阶段，设计一个合理的仿真场景，通过计算机仿真，验证本文提出的采用优化算法解决气动刹车问题的可行性。仿真参数及初值如表1所列。

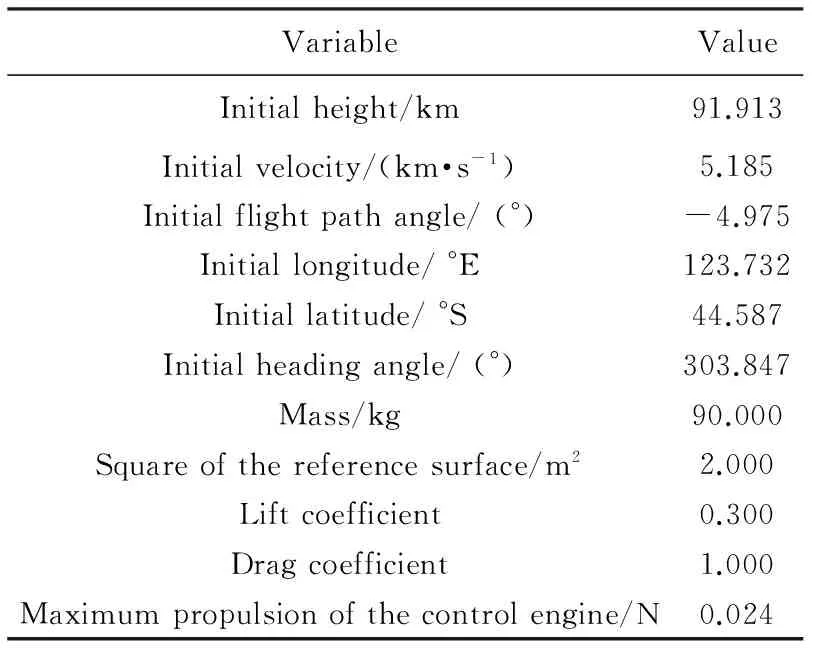
表1仿真参数及初值表

整个仿真过程耗时较长，且每一圈远拱点高度的变化规律相似。为了得到清晰的图像，故重点模拟仿真飞行器从初次进入火星大气实现气动刹车后的37个周期内的情况，仿真结果如图3所示。其中，3个坐标轴的坐标分别满足x=rcosφcosθ,y=rcosφsinθ和z=rsinφ。气动刹车过程中及气动刹车结束后目标轨道高度随时间变化情况，分别如图4和图5所示。过载随时间的变化情况，如图6所示。其中，过载为加速度a与地球海平面高度下重力加速度g的比值。由于相邻的两个周期内轨道变化不是十分明显，所以图3中会有类似曲线形成的两个椭圆之间的重叠区域，实际上是从偏心率较大的椭圆轨道逐渐变为偏心率小的椭圆轨道。

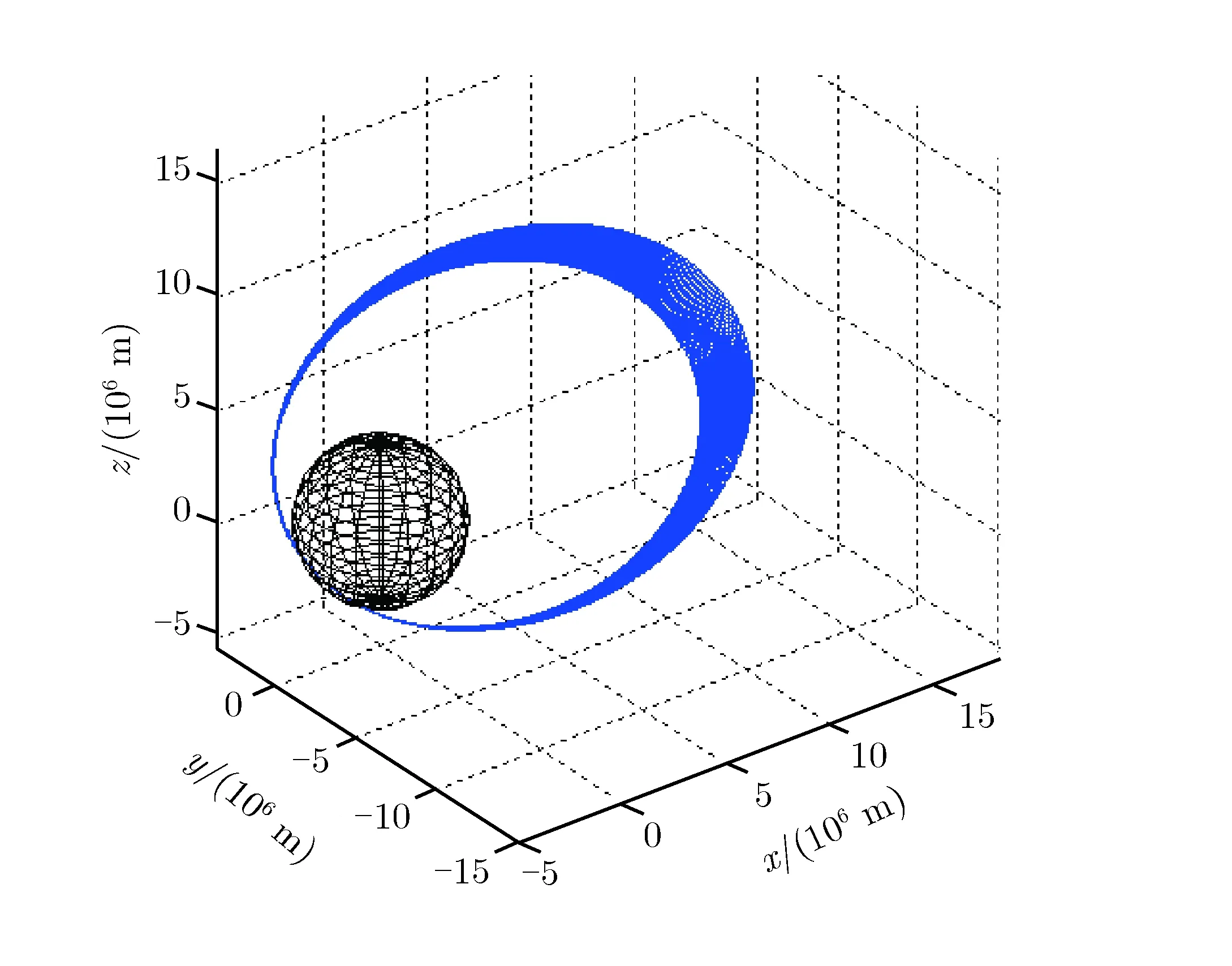
图3初始阶段轨道仿真结果Fig.3Simulation result of the trajectory of the initial stage

图4气动刹车过程中目标轨道高度随时间的变化Fig.4 Height of the target orbit vs.time during aerobraking

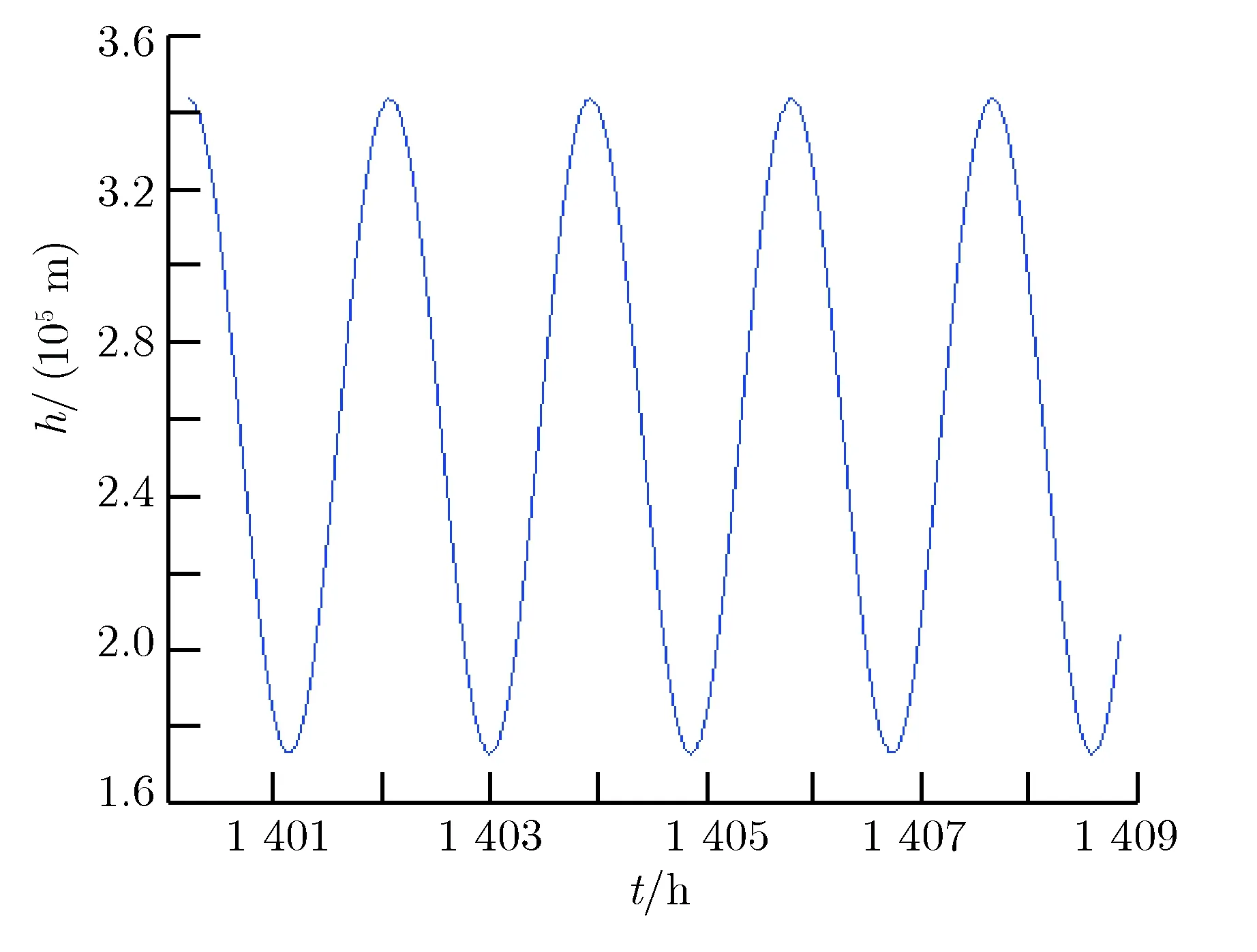
图5气动刹车结束后目标轨道高度随时间的变化Fig.5Height of the target orbit vs. time after aerobraking

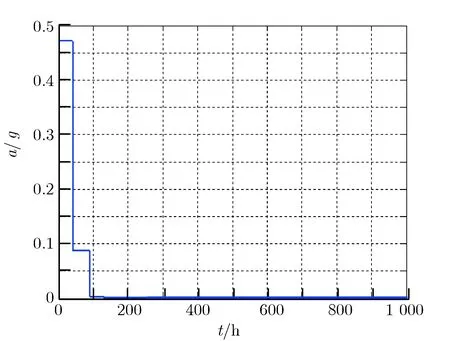
图6过载随时间的变化曲线Fig.6Overload vs. time

从图4至图6可以发现，在气动刹车过程中，椭圆轨道远火点的高度逐步缓慢下降，而近火点高度则在优化得到的脉冲机动下基本保持不变。最后几圈的结果表明，飞行器轨道已保持在某一相对固定的椭圆目标轨道上，由于初始时刻飞行器以一个较高速度通过火星大气比较稠密的底层，所受过载较大，经过几个周期变轨调整，飞行器通过的是火星上层十分稀薄的大气，所受过载值很小，整个气动刹车过程，过载均小于3g，满足设定要求。

4结论与展望

虽然通过气动刹车方式实现变轨耗时较长，但可以在很大程度上节约燃料，在非载人火星探测任务中应用前景可期。基于GPOPS优化算法，本文设置速度增量为优化变量，并限定约束条件，计算每

个周期实现气动刹车后维持近火点轨道高度所需的速度增量，通过仿真实验，证明该方法可以完成气动刹车变轨的功能，并满足过载等约束条件要求。所以，基于GPOPS优化设计的气动刹车方案合理可行，为气动刹车领域的研究提供了一种新的思路。在未来可以进一步研究利用GPOPS算法使用小推力发动机连续工作的方式实现气动刹车的方案，从而使气动刹车的方案更好地适应实际任务的需求。

[1]CARR M H, GARVIN J. Mars exploration [J]. Nature, 2001, 412(6 843): 250-253.

[2]SAUNDERS R, SPEAR A, ALLIN P, et al. Magellan mission summary [J]. Journal of Geophysical Research: Planets, 1992, 97(E8): 13 067-13 090.

[3]LYONS D T, BEERER J G, ESPOSITO P, et al. Mars global surveyor: Aerobraking mission overview [J]. Journal of Spacecraft and Rockets, 1999, 36(3): 307-313.

[4]SAUNDERS R, ARVIDSON R, BADHWAR G, et al. 2001 Mars Odyssey mission summary[J]. Space Science Reviews, 2004, 110(1/2): 1-36.

[5]GRAF J, ZUREK R, JONES R, et al. An overview of the Mars reconnaissance orbiter mission[C]//2002 IEEE Aerospace Conference Proceedings, Big city, MT, 2002.

[6]HALL N. Mars Atmosphere Model-Meric Units [EB/OL] [2016-6-18]. http://www.grc.nasa.gov/ WWW/k-12 /airplane/atmosmrm.html.

[7]KUMAR M, TEWARI A. Trajectory and attitude simulation for aerocapture and aerobraking[J]. Journal of Spacecraft and Rockets, 2005, 42(4): 684-693.

[8]ZHANG W P, HAN B, ZHANG C Y. Spacecraft aerodynamics and trajectory simulation during aerobraking [J]. Appl Math Mech, Engl Ed, 2010, 31(9): 1 063-1 072.

Aerobraking Trajectory Design for Mars Mission Using Gauss Pseudospectral Optimization Software

HUANG Feng,HUANG Yue-chen,LI Hai-yang

(National University of Defense Technology,Changsha410073,China)

Based on the background of future Mars exploration, merits and demerits of the trajectory transfer method of aerobraking are discussed. An improved exponential Martian atmospheric model is chosen. Then a dynamic model of aerobraking is established. Constraint conditions are set according to the restrictions of the spacecraft and the orbit. Change in velocity of each circle of aerobraking to maintain the altitude of the periapsis is obtained by GPOPS. Thus, the goal of entering the target orbit by using aerobraking method is achieved. The results indicate that the scheme of aerobraking obtained by the optimal calculation of GPOPS is available and it provides a new way for future study of aerobraking.

Mars exploration;Gauss pseudospectral method;trajectory simulation；

2016-01-15；

2016-06-24 基金项目：国家自然科学基金资助项目(11372345) †通信

李海阳(1972- )，男，河北大城人，教授，博士，主要从事载人航天系统分析与仿真研究。

E-mail:neilblue2011@hotmail.com

V412.4

A

2095-6223(2016)031003(5)