主成分分析与线性判别分析两种数据降维算法的对比研究

董虎胜

（苏州经贸学院，苏州　215009）

主成分分析与线性判别分析两种数据降维算法的对比研究

董虎胜

（苏州经贸学院，苏州215009）

在模式识别与机器学习中，为了降低高维数据带来的巨大运算量，通常需要对数据进行降维预处理。在常用的数据降维算法中，主成分分析（PCA）与线性判别分析（LDA）是两种最常用的降维方法。由于这两种算法具有较强的内在联系而不易理解，对这两种算法的工作原理与实现进行对比分析，并对两者的应用与扩展进行讨论。

机器学习；数据降维；PCA；LDA

苏州经贸学院科研项目（No.KY-ZR1407）

0　引言

在模式识别与机器学习的研究与应用中，经常需要面对高维的数据，例如计算机视觉中进行人脸识别与行人检测、生物信息学中对蛋白质结构预测时，为了获得关于目标对象更为丰富的信息，所提取的样本通常达到上千或上万维度。另外，为了能够统计分析出数据内在的模式，在研究中我们希望数据量越多越好。而且在很多应用中，数据样本是每时每刻都在增加的，例如视频监控所记录的画面、天气预报系统所记录的气候资料、网络购物平台的交易数据等。如此大量、高维的数据在分析研究时给运算处理带来了相当高的难度。尽管目前硬件设备的运算能力已经得到大幅提升，但在处理海量高维数据时仍然力不从心。大数据的存储传输、“维数灾”等困扰也由此而来。

为了应对这种挑战，人们在处理大量的高维数据时已经提出一些解决方案，例如基于分布式运算的Hadoop、MapReduce，基于稀疏表达的压缩感知等。另一类更为广泛应用的处理手段即为数据降维，其思想是从原始数据中抽取最具有判别力的维度，或者是通过变换的手段将样本由原始空间投影到低维空间，但尽可能地保持原有数据在某方面的结构或性质。在高维样本中一些维上可能有强相关性，而且会存在大量的噪声，通过降维不仅可以带来运算量上的降低，还可以实现降噪与去相关。因此，目前数据降维技术广泛地应用于数据样本的预处理中。

在数据降维处理中，比较常用且有效的方法为线性变换技术，即通过线性投影将原样本数据投影到低维子空间中，其中典型的有PCA与LDA。本文对这两种技术的实现原理与应用进行了对比分析研究，并对两者的扩展也进行了讨论。

1　主成分分析PCA

PCA是一种无标签的数据降维种方法，其目标是通过线性投影将高维数据映射到低维空间中表示，但同时满足在所投影的子空间中，各维度上数据的方差保持最大化。由此实现使用较少的维度表示原始数据，但保留原始数据各维度的分布特性。由于方差信息的保留，也使得PCA是数据降维技术中对于原始数据信息丢失最少的一种线性降方法。

设原始样本为X∈Rd×n，其中d为样本维度，n为样本数，第i个样本表示为xi。根据PCA的最大方差的目标，我们需要求得一个投影矩阵W∈Rd×d'，其中d'≤d，为了求得W，设W=［w1，w2，…wk，…，wd'］，其中wk∈Rd为一单位投影向量，即由于投影后的新样本为在新的d'维度子空间的表达，因此WT即为过渡矩阵，亦即d'空间的基，这里我们要求各个基为标准正交基，即＜wk，wl>=0（k≠l）。由此可以建立下面的目标函数：

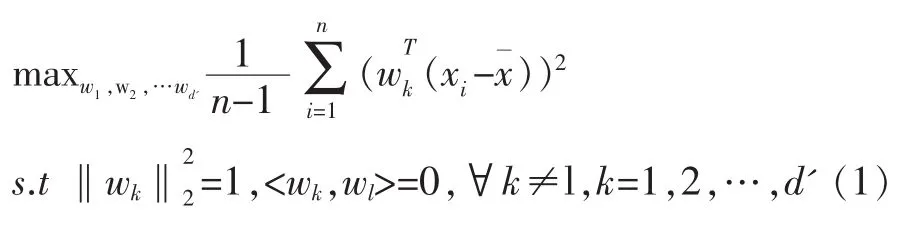
其中C为样本的协方差矩阵，即：

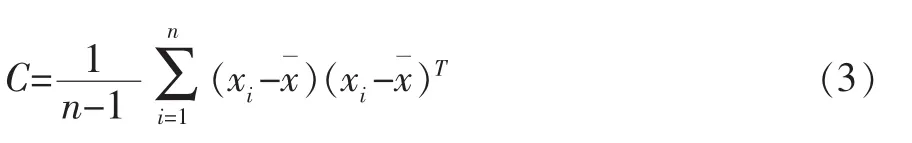
式（3）为一等式约束的最优化问题，可以采用Lagrange乘子法进行求解。我们可以建立如下的Lagrange方程：

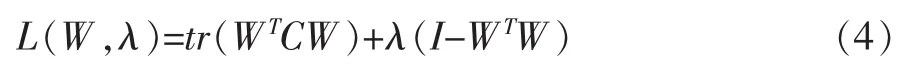
对式（4）求关于W的导数有：

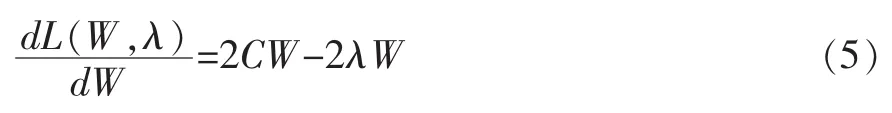
并令其为0，可得CW=λW。考虑W的第k列wk，可以发现Cwk=λwk为一特征值求解问题，若将C的各特征值按由大到小排序，wk即为第k个特征值所对应的特征向量。所以只需对C作特征值分解后，将特征值按降序排序后，取前d'个特征向量拼合后即获得W。由于数值求解中，使用奇异值（SVD）分解可以获得更好的数值稳定性，因此也可以对协方差矩阵C采用SVD分解：

其中U为由左特征向量组成的矩阵，∑为一对角矩阵，其对角线元素为各奇异值，V为由右特征矩阵。采用SVD分解的另一个优势在于分解后∑中各奇异值已经按降序排序，我们可以直接取左特征值矩阵U的前d'列即为W。

由上述求解过程可知，若要对样本矩阵作PCA降维处理，可以采用如下的步骤：

（2）计算样本的协方差矩阵；

（3）对协方差矩阵作特征值分解，将特征值按降序排序，并取前d'个特征值所对应的特征向量组成投影矩阵W，当然，也可以采用上面介绍的SVD分解方法；

（4）计算X'=WTX，X'∈Rd'×n即为投影后的新样本矩阵。

在实际应用中，对于新维度d'的设定上，可以根据需要手工指定，也可以根据所截取的特征值之和占所有特征值和的比率来确定，这种确定特征值的方法也被称为能量（或贡献率）确定法。若取能量保留100%，即为完全能量的PCA投影，此时投影后样本的维度为min（n，d）-1。

2　线性判别分析LDA

LDA的出发点与PCA类似，同样是将样本由高维空间投影到低维空间，但其在保留原有数据的特性上与PCA存在差异。LDA要求投影后的样本点能够实现属于同一类别的样本之间的距离更小，而不同类别的样本点在投影后的空间中距离更远，从而实现在低维子空间中将不同的类别样本区分开的目标。因此LDA是一种带有标签的降维技术。

设样本矩阵X∈Rd×n中有c个类别，其中属于第i类ωi的样本有ni个各类别样本的中心点为所有样本的中心点为若投影矩阵为W∈Rd×d'，则投影后的样本为Z=WTX，投影后的第i类Ωi中心点为所有样本的中心点为

根据LDA的类内紧致、类间疏远的思想，定义投影后新样本空间中类间离散度JB为：

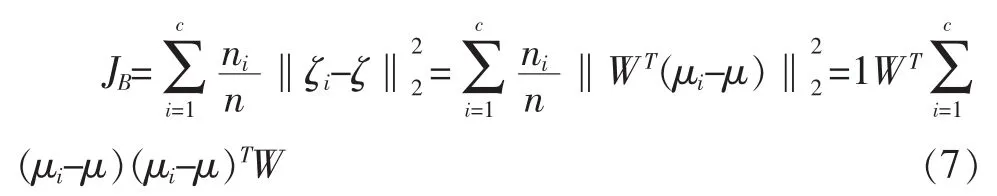
定义投影后的样本的类内紧致度JW为：

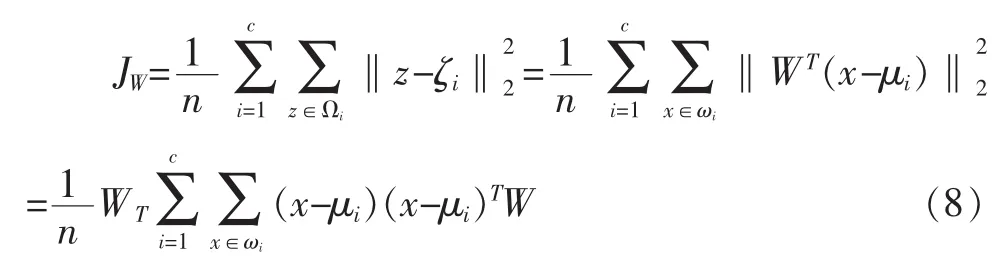
其中JB度量了各个类别的中心点到所有样本中心间的距离且由对各个类进行了加权，JW则度量了所有类别样本距离自己所在类的中心点的距离。为了便于表达，可定义类间散布矩阵SB与类内散布矩阵SW为：

从而可将JB与JW简化为：

根据Fisher判别准则可建立目标函数为：

与PCA类似，考虑W的第k列wk，此时上式转化为：

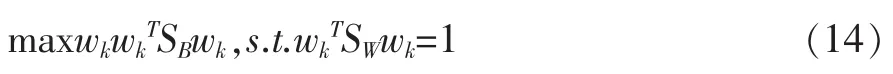
建立Lagrange方程：

对wk求导并令导数为0，可解得SW-1SB=λwk，即wk为S与S的广义特征向量。为了使得BW取值最大，只需取SW-1SB前k个最大特征值所对应的特征向量即可拼得W。但是由于SB的秩最大为c-1，因此k≤c-1，即LDA最多只能投影到c-1维的子空间中。

由上述的LDA的推导可以归纳出使用LDA进行数据降维及分类的过程为：

（1）根据给定样本矩阵计算各类样本的中心点与所有样本的中心点；

（2）计算各样本内类散布矩阵SW与内间散布矩阵SB；

（3）对SW-1SB作特征值分解，将特征值按降序排序，并取前k个特征值所对应的特征向量组成投影矩阵W，当然，也可以采用SVD分解方法；

（4）计算X'=WTX，X'Rd'×n即为投影后的新样本矩阵。

3　PCA与LDA的差异与联系

从整体上说PCA与LDA同属于降维方法，而且两者在求解投影矩阵时均转化为求解特征值问题，两者具有比较强的相似性。在应用中，PCA与LDA也常结合使用，即首先使用PCA进行无监督降维，再使用LDA进行有监督的降维及分类。为了取得比较好的效果，在应用这两者之前最好进行去数据规范化处理。但PCA在工作中无需样本的类别信息，因此属于无监督的降维，而LDA在工作中需要利用样本的类别标签，所以其属于有监督的降维。此外，两者的差异主要有：

（1）PCA的目的是使投影后的样本在各个维度上方差保持最大，而LDA在投影后则是要求各个类别之间尽可能分得开。

（2）在使用PCA时，降维后的维度可以根据需要指定，但对于LDA降维后最大不能超出c-1维。

（3）从上面的推导还可以看出PCA的投影矩阵在求解中是要求各个列（即新空间中的各个基向量）都是单位正交的，但对于LDA却没有施加此约束。也就是LDA仅考虑投影后样本类别间的差异而不考虑是否坐标系为正交。

图1给出了PCA与LDA对于2维示例样本的投影结果比较。由图中可以看出PCA的投影方向与LDA的投影方向明显不同。PCA投影后的样本的方差信息得了最大程度的保留。而对于LDA来说，选择的是能够把两类样本更区分开的方向。

4　PCA与LDA的扩展方法

从对PCA与LDA的推导中可以看出，两者本质上均为将原始样本线性投影到低维子空间中，但这对于一些存在非线性结构的数据处理上却存在不足，为了对这类数据的降维，研究人员提出了基于核方法的KernelPCA［4］与KernelLDA［5］。另外，虽然PCA能够降噪与去相关，但对于大的噪声与严重的异常点，PCA却不能良好应对，而RobustPCA［6］则可以较好地处理，因为它假设噪声是稀疏的而不考虑噪声的强弱。对于LDA来说，其对于服从高斯分布的数据具有比较好的降维效果，但在样本不服从高斯分布时效果则不够理想，但此时可以将局部信息引入从而发展出带局部信息的LDA（Local Fisher Discriminant Analysis，LFDA）［7］或考虑边缘样本关系的MFA（Marginal Fisher Analysis）［8］。

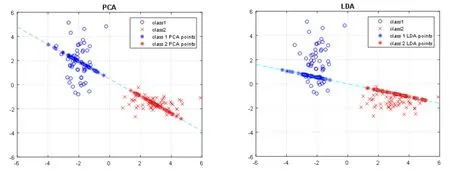
图1　PCA与LDA对2维数据的降维对比

5　结语

PCA与本文对PCA与LDA两种常用的线性变换降维技术进行了对比分析研究，并根据实验对两者的联系与区别进行了详细的讨论。此外，本文还对这两种方法的扩展进行了简要的阐述。作为数据分析中重要的降维技术，基于PCA与LDA思想的数据降维方法也还在不断发展之中。

［1］杨淑莹.模式识别与智能计算：MATLAB技术实现（第2版）.北京：电子工业出版社，2011.8.

［2］R.O.Duda，P.E.Hart，李宏东等译.模式分类（第2版）.北京：机械工业出版社，2003.9.

［3］C.M.Bishop.Pattern Recognition and Machine Learning，Springer，2006.

［4］Sch lkopf B，Smola A，Müller K R.Kernel Principal Component Analysis［J］.Advance in Kernel Methods-Support Vector Learning，2009，27（4）：555-559.

［5］Ye Fei，Z.Shi，and Z.Shi.A Comparative Study of PCA，LDA and Kernel LDA for Image Classification.IEEE International Symposium on Ubiquitous Virtual Reality，2009：51-54.

［6］Candès E J，Li X，Ma Y，et al.Robust Principal Component Analysis［J］.Journal of the ACM，2011，58（3）：1-73.

［7］Sugiyama M.Dimensionality Reduction of Multimodal Labeled Data by Local Fisher Discriminant Analysis［J］.Journal of Machine Learning Research，2007，8（1）：1027-1061.

［8］Yan，Shuicheng，et al.Graph Embedding and Extensions：A General Framework for Dimensionality Reduction.IEEE Transaction on Pattern Analysis and Machine Intelligence，2007，29（1）：40-51.

Machine Learning；Dimension Reduction；PCA；LDA

Comparative Analysis of Two Dimension Reduction Algorithms of PCA and LDA

DONG Hu-sheng
（Suzhou Institute of Trade and Commerce，Suzhou 215009）

To lower the heavy computation induced by high dimensional data in pattern analysis and machine learning，the data is often preprocessed by dimension reduction methods.In the dimension reduction algorithms，Principle Component Analysis（PCA）and Linear Discriminative Analysis（LDA）are two most important and widely used methods.However，they are easily to be confused for the inherent relationship.Presents a detailed comparative analysis of their working principle and implementation，furthermore，discusses their application and extension.

1007-1423（2016）29-0036-05

10.3969/j.issn.1007-1423.2016.29.008

董虎胜（1981-），男，讲师，研究方向为机器学习与计算机视觉

2016-08-11

2016-10-20