基于模糊自适应差分进化算法的机器人手臂运动控制研究

李荣，王华君，徐燕华，孟德建

基于模糊自适应差分进化算法的机器人手臂运动控制研究

李荣，王华君，徐燕华，孟德建

现实应用中机器人机械手需要精确的运动控制来操作目标，针对机械手运动的高度非线性和复杂的运动模型，提出了一种基于模糊自适应差分进化（FADE）算法的机器人手臂运动控制方案。利用进化过程来获取运动模型的最优解，利用模糊逻辑控制器自适应调节突变因子（F）和交叉率（CR），避免进化过程过早收敛陷入局部最优解。以CRS A456机械手为实验对象，实验结果表明，与最小二乘法和传统差分进化方法相比，FADE方案具有最优的估计性能。

机械手臂；机器人；模糊自适应控制；差分进化算法；参数估计；运动控制

0　引言

最近，机器人技术已经应用到临床医学领域，这就需要足够准确的机器人动态参数来设计控制系统[1]。研究已表明，差分进化（DE）算法收敛速度比遗传算法、粒子群优化快，然而，DE的参数仍然对控制参数敏感，如突变因子（F）和交叉率（CR）[2]。

本文以CRS A456机器人机械手为研究对象，提出一种基于模糊自适应差分进化（Fuzzy Adaptive Differential Evolution，FADE）算法的控制方案，利用模糊逻辑控制器自动调节变异参数（F和CR），根据种群的多样性计算模糊系统的输入信号，实现较高的计算效率和自适应优化性能。

2　CRS A456　机械手动态模型

CRS A456机器人机械手的简单结构如图1所示：

机械手需要能够拿起外科手术钻孔工具，需要5个自由度，因此，考虑机械手臂前5个关节的建模。

本文利用L-E方程推导机器人机械手运动方程。L-E是一种非递归算法，以此可以得出，作用在任何关节轴的扭矩为公式（1）：

式中，τi为第i个关节的扭矩，i=1,2,...,N。N为自由度数量，q,,分别为机器人关节的位置、速度和加速度，X为模型参数，Dij为惯性耦合，Hijk为向心力和科氏力，Gi为重力负载，τfi为关节摩擦力。

文献[3]通过式（1）描述了系数Dij和Hijk，证明了机器人运动方程是线性的。每个节点的质量、重心和惯性乘积如图2所示：

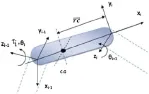
图2　单节点CRS A465坐标结构

式（1）描述了当运动方程参数X为质量、重心位置和节点惯性时，方程具有线性特征。因此，该方程可以变形为公式（2）：

为了对不同估计模型的性能进行比较，本文仅考虑CRS 456单关节手臂参数估计问题。CRS 456单关节手臂仅定义4个参数ai,i=1,...,4；它们分别为惯性、粘滞摩擦系数、正库伦摩擦和负库伦摩擦。因此，系统运动方程可变形为公式（3）：

式中，τ为扭矩，X为已减少到4个参数的质心参数，它们分别为角加速度x1，角速度x2，正值速度x3（如果x2为正，则x3=1，否则x3=0）和负值速度x4（如果x2为负，x4=1，否则x4=0）。

2　自适应运动控制

文献[5]采用模糊逻辑控制（FLC）来控制DE的变异因子F和交叉率CR，利用基于模糊知识的系统在线更新控制参数。该算法提出首先要解决DE中两个问题：过早收敛和停滞[6]。提出的FADE解决了上述问题，其步骤如下：

2.1初始化

使用标准函数的候选解决方案初始化种族数量如公式（4）：

式中，Xmax,j和Xmin,j为参数值的上界和下界，该值可以定义来自的特定区域；在初始化种群数量时，选择每个NP向量的j∈｛1,...,D｝。αi,j为一个随机数生成器，它返回[0,1)之间均匀分布的实数。

2.2突变

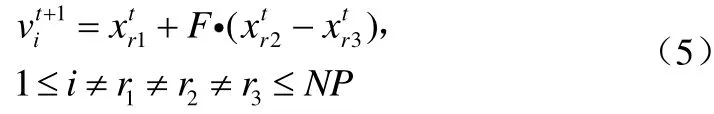
2.3交叉

式中，βi,j为[0,1]之间的均匀实数。jrand为[1,D]之间随机生成的整数，且确保实验向量Ui(t)与其对应的目标向量Xi(t)至少有一个组件不同。

2.4选择

使用一对一的贪婪算法决定实验向量Ui(t)是否战胜其对应的目标向量Xi(t)。赢家将为下一代种群Xi(t+1)的成员。该竞争通常是根据两个独立的适应度函数决定如公式（7）：

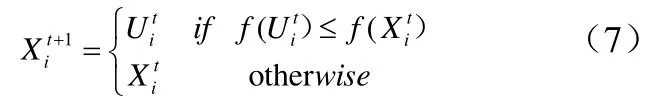
2.5自适应模糊控制

FADE控制参数对应于种群信息，即函数值或种群多样性（FC），参数向量（PC）和第 t代以后它们的更新值。两个FLC系统用于作为模糊控制机制的基础。FADE算法的自适应步骤如下：

Step 1 （初始化）：计算FC和PC的值且作为式（8）和（9）中FLCs的输入值，控制参数（F和CR）的值为输出值如公式（8）、（9）：

公式中，PC参数向量，缩放到[0,1]之间作为D1，缩放到[0,2]之间作为D3；FC为函数值，缩放到[0,1]为D2，缩放到[0,2]为D4；为第 t代函数值向量的第 i组件，i=1,2,...,NP；为第t代参数矩阵XNP×D的第i行第j列组件，i=1,2,...,NP，j=1,2,...,D；t为代的序列号；NP和D分别表示种群大小和问题的维数如表1所示：

表1　隶属度函数（fg 为高斯隶属度函数）

Step 2 （模糊化）：F和CR的值被分配给模糊隶属度函数，如图3所示：

图3　输入和输出变量D1，D2，D3，D4，F，CR的隶属度函数

图 3（a-d）表示针对D1，D2，D3和D4的模糊隶属度函数。图3（e和f）表示输出变量F和CR的隶属度函数。

Step 3（规则库）：IF-THEN模糊规则用于制定由模糊逻辑组成的条件状态。每个变量（D1，D2，D3，D4，F，CR）拥有对应的带有3个模糊子集的模糊隶属度函数，其中S为“small”，M为“middle”，B为“big”，如表2所示：

表2　模糊规则（S=small; M=medium; B=big）

所有输入和输出的模糊决策面如图4所示：

图4　联合输入输出的模糊决策曲面

该表面是非线性的且单一的，表示给定输入的模糊决策表面。

Step 4 （模糊推理机）：本文采用文献[8]的模糊推理方法作为模糊控制策略。该方法的模糊策略通过规则将给定输入映射到输出（模糊集）。

Step 5 （去模糊化）：去模糊过程是一种将模糊输出空间映射到真实输出的过程，模糊集中的输入和输出为单一值[9]。FADE将几何中心去模糊化技术（CDT）作为去模糊化策略。

3　实验结果及分析

将CRS A465单关节臂模型作为实验对象，CRS 465单关节手臂需要估计A=4个参数。仿真实验中，a1为惯性，a2为粘性摩擦参数，a3为正库伦摩擦，a4为负库伦摩擦。

在开发新型基于FADE的动态参数识别框架过程中，必须注意以下几点。

（1）个体（解决方案的编码）和种群的表示：包含popsize(NP=30)个体的种群是指每代个体的数量。首先，将个体结构中需要参数估计的必要信息进行编码，每个个体表示一个完整的解决方案，拥有4个实数编码参数。

（2）参数控制：控制参数为突变率F和交叉率CR。在标准DE/rand/1/bin中，这两个参数分别为0.5和0.9。在FADE中，这些参数通过模糊自适应系统进化，将较优参数生成较优的个体，从而产生后代，且将较优的参数值传播给后代。

（3）个体进化（验证解决方案）：适应度函数。根据估计模型的均方误差（MSE）来估计每个个体的适应度如公式（10）：

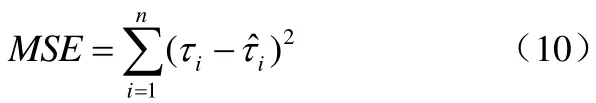
（4）停止判则：最常见的停止条件为最大迭代次数。当搜索空间较大时，较小的迭代次数可能不能获取最优解；另一方面，较大的迭代次数也会浪费计算资源。标准DE和FADE迭代次数设为100.

最小二乘法（OLS）识别方法通过最小化实际扭矩τ和预测扭矩ΦXOLS的均方误差来估计未知参数XOLS，方程如公式（11）：

使用上述方法估计其对应的CRS 465单关节质心参数。3种估计方法的实验结果，这些结果为30个个体的平均值如表3所示：

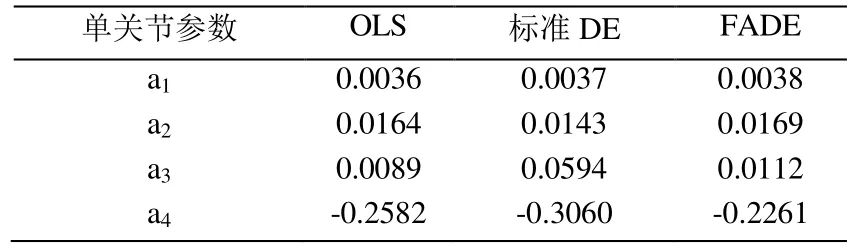
表3　单关节CRS A465机器人手臂的质心参数估计

在均方根误差和方差方面几种算法的实验结果比较如表4所示：

表4　不同估计模型的均方根误差和标准偏差

从表中可以看出，FADE性能优于OLS和标准DE算法。这是因为FADE更新了每代控制参数值，有效的处理了噪声等问题。

100代中的F和CR值如图5所示：

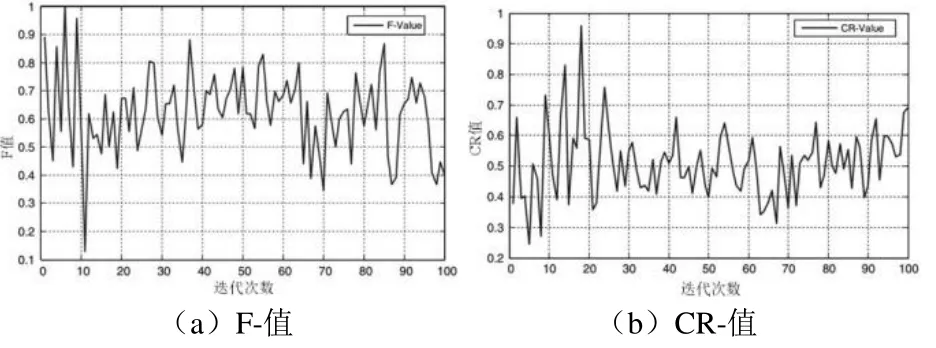
图5　100次迭代的FADE算法的F和CR值

从图中曲线可以看出，开始阶段存在明显的波动，然后开始趋于稳定。F和CR值的改变有助于避免FADE陷入局部最优。

4　总结

本文利用模糊自适应差分进化算法（FADE）估计单关节CRS A465机器人手臂动态模型的质心参数，使用模糊逻辑控制调节参数F和CR的值，实现较高的计算效率和自适应优化性能。实验中，分别使用本文方法、OLS和标准DE方法估计单节点CRS A465机器人的质心参数，结果表明，FADE性能最优。

为了进一步研究FADE的性能，未来会考虑增加机器人手臂的关节，同时增加预测模型的参数数量。

[1] 赵明炬. 模糊控制运用于轮型机器人的目标追踪[J].计算机测量与控制,2014,22(2): 614-616.

[2] 刘正雄,鹿振宇,黄攀峰. 基于递推差分进化算法的空间机器人参数辨识[J]. 宇航学报,2014,35(10): 1127-1134

[3] Kumar V,Mittal A P,Singh R. Stability analysis of parallel fuzzy P+ fuzzy I+ fuzzy D control systems[J]. International Journal of Automation and Computing,2013,10(2): 91-98.

[4] Al-Dabbagh R D,Kinsheel A,Mekhilef S,et al. System identification and control of robot manipulator based on fuzzy adaptive differential evolution algorithm[J]. Advances in Engineering Software,2014,78(3): 60-66.

[5] Islam S M,Das S,Ghosh S,et al. An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization[J]. Systems,Man,and Cybernetics,Part B: Cybernetics,IEEE Transactions on,2012,42(2): 482-500.

[6] 毕晓君,刘国安,肖 婧. 基于新变异策略的动态自适应差分进化算法[J]. 计算机研究与发展,2012,49(6): 1288-1297.

[7] 郑亚青,江晓玲. 基于最小二乘支持矢量机的四绳牵引 6 自由度欠约束并联机器人的静刚度分析及优化[J]. 机械工程学报,2013,48(13): 49-55.

[8] Cazarez-Castro N R,Aguilar L T,Castillo O. Designing type-1 and type-2 fuzzy logic controllers via fuzzy Lyapunov synthesis for nonsmooth mechanical systems[J]. Engineering Applications of Artificial Intelligence,2012,25(5): 971-979.

[9] 钱夔,宋爱国,章华涛,等. 基于自适应模糊神经网络的机器人路径规划方法[J]. 东南大学学报: 自然科学版,2012,42(4): 637-642.

Adaptive Motion Control Scheme of Robot Manipulator Using FADE Algorithm

Li Rong,Wang Huajun,Xu Yanhua,Meng Dejian
(School of Engineering,Taihu University of Wuxi,Wuxi 214064,China)

The robot manipulator needs precision motion control to operate target in practical application. For the issues that the movement of manipulator is a highly nonlinear and complex motion model,a robot manipulator adaptive control scheme based on fuzzy adaptive differential evolution (FADE) algorithm is proposed to estimate the dynamic parameters of robot arm. It uses evolutionary process to obtain the optimal solution of motion model,and uses adaptive fuzzy logic controller to adjust the mutation factor (F) and crossover (CR) adaptively so as to avoid the premature convergence of evolution into a local optimal solution. By using CRS A456 manipulator as the experimental object,the experimental results show that,compared with the least square method and traditional differential evolution method,the estimation performance of FADE scheme is the best.

Robot Manipulator; Fuzzy Adaptive Control; Differential Evolution Algorithm; Parameter Estimation; Motion Control

TN241

A

1007-757X(2016)03-0027-03

江苏省高校自然科学研究项目（14KJB520036）

李 荣（1978-），女（汉）淮安人，无锡太湖学院，工学院，讲师，硕士，研究方向：机器人控制、模式识别等，无锡，214064

王华君（1979-），男（汉），宜兴人，无锡太湖学院，工学院，讲师，硕士，研究方向：机器人控制、模式识别等，无锡，214064

徐燕华（1979-），女（汉），无锡人，无锡太湖学院，工学院，讲师，硕士，研究方向：机器人、模式识别等，无锡，214064

孟德建（1979-），男（汉），扬州人，无锡太湖学院，工学院，讲师，博士，研究方向：机器人、移动互联感知、视频处理等，无锡，214064

（2015.08.11）