一种利用Duffing-VanderPol振子估计弱信号相位的方法*
孙文军,芮国胜,王 林,田文飚
一种利用Duffing-VanderPol振子估计弱信号相位的方法*
孙文军**,芮国胜,王 林,田文飚
(海军航空工程学院电子信息工程系,山东烟台264001)
根据Duffing-VanderPol振子大周期态时的最大LYaPunov指数与系统策动力的关系,提出了一种基于该振子检测微弱信号相位参量的方法。该方法利用系统策动力与待测信号初始相位有关的特性,得到待测信号的初始相位,并将相位检测过程中噪声对系统的影响作为影响因子加以考虑。理论分析及数值仿真结果表明,该方法工程实现简单,抗噪性能好。当待测信号信噪比为-30 dB时,均方误差仅为0.1,具有较高的估计精度。
微弱信号检测;相位检测;Duffing-VanderPol振子;LYaPunov指数
1 引 言
随着现代数字通信技术的发展和各种应用领域的需要,强噪声背景下微弱信号的检测已成为研究的重点。由于混沌振子对小信号的极端敏感性和对噪声的免疫力,混沌理论在微弱信号检测中得到了广泛应用[1-4]。在不同背景噪声下,出现了各种基于混沌振子的微弱信号检测理论和方法[5-6],由于混沌振子检测具有灵敏度高、抗噪声能力强、设备成本低的特点,因而受到人们的广泛关注。
许多研究者对这一领域进行了深入研究。文献[7]利用混沌振子法实现了对低信噪比环境下频移键控信号解调;文献[8]将多混沌振子阵列应用于信号的检测,实现了信号在不同初始相位下的检测。近年来,弱信号检测领域利用混沌振子的参数敏感特性取得了一些新的研究成果:文献[9]通过对水声信号的非线性特征进行分析并对其进行系统建模,将微弱水下目标信号的检测能力提升了约10 dB;文献[10]将自相关和混沌理论相结合,进一步增强了混沌振子的弱信号频域检测能力;文献[11-12]基于主动控制策略,通过设计比例微分控制器消除误差系统中的非线性项,以获得混沌系统的准确同步。这些研究成果展示了混沌振子在弱信号检测领域尤其是参数辨识等方面具有巨大的潜在研究价值,但仍存在一些问题:一方面,大多数文献更多关注的是弱信号是否存在的物理检测,而未对信号的相位检测进行论述;另一方面,基于数值分析理论的控制类方法需要设计复杂的代价函数,实现难度大,无法实现快速判决。
微弱信号的相位检测一直是弱信号检测领域一个非常重要的问题。本文通过对Duffing-Vander_ Pol振子在大周期态时的LYaPunov指数进行研究,得到其与系统策动力的关系,为了能够在较低信噪比条件下获得较好的检测性能,考虑了信号噪声的影响,得到信号等效策动力与信号相位的关系,最终得到LYaPunov指数与待检测信号相位的关系。仿真实验结果表明,该方法具有较高的检测精度,并且有较好的抗噪声性能。
2 Duffing-Vanderpol系统信号检测原理
考虑如下Duffing-VanderPol方程的弱信号检测基本形式:

式中:ω为待检测周期信号的频率;k为阻尼比;-x(t)+x3(t)为非线性恢复力;fcos(ωt)为内置周期策动力;rcos(ωt+Δφ)是待测周期弱信号;n(t)为噪声信号。传统的信号检测方式以Duffing-Vander_ Pol系统对噪声免疫[13]为前提,将待测信号作为混沌系统周期策动力的摄动,在噪声强烈的情况下,对系统状态的改变影响很小,而一旦有特定频率的待测信号,由于混沌系统对周期小信号的敏感性,即使幅值较小,也会使系统发生相变,在相位差满足如下条件时,即π-arccos(r/(2f))≤Δφ≤π+arccos(r/(2f)),通过判断系统是否发生了相变来判定信号是否存在,从而达到在强背景噪声下对微弱周期小信号进行检测的目的。上述信号检测方法对信号相位只考虑了一定的检测范围,没有具体的相位差值。可应用多个内置不同初始相位策动力的混沌振子组成的阵列,对未知相位正弦信号进行并行检测,其检测原理如图1所示。

图1 Duffing-VanderPol振子阵列检测原理图Fig.1 The detection sYstem comPosed of multiPle Duffing-VanderPol oscillators arraY
图1 中,通过n个不同初始相位的振子检测,对每个振子是否相变进行判断,综合振子的状态可以将待检测信号的相位确定在一个较小范围内,从而达到弱信号相位检测的目的。这种检测方法使用的Duffing-VanderPol方程数量越多,检测出的信号相位范围越小,系统的灵敏度也越高,但是随着方程数量的增多,检测复杂度会大大增加,降低了检测效率,并且此方法也没有考虑到噪声对系统相变判断的影响。
3 本文相位检测方法
本文综合考虑Duffing-VanderPol系统LYaPunov指数与周期策动力的关系以及周期策动力与相位检测的关系,提出基于Duffing-VanderPol振子的正弦信号相位检测方法。
3.1 待检测信号相位与幅值关系
由式(1)等号的右端可知,对混沌振子起相变作用的总周期驱动信号为

式中:

由于待测信号的幅值r远远小于策动力临界值f,由式(4)可知,Δθ很小,所以对系统状态的影响可以忽略不计,因此系统状态是否改变的关键在于Fs与噪声干扰n(t)的大小。由式(3)可知,系统是否会发生相变与待检测信号和内部驱动信号的相位差有关,由于式(3)中cosΔφ与Fs存在非线性关系,不便于对相位进行估计,所以对其进行线性化可得
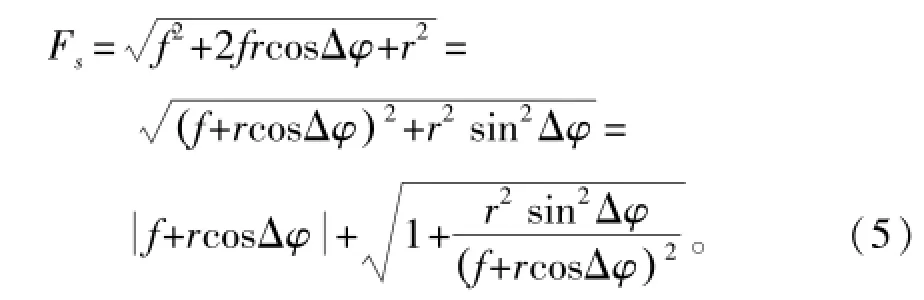
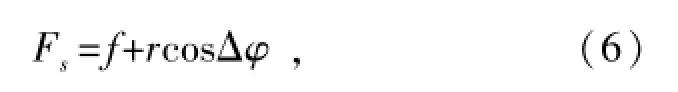
进一步可得

通过上式可知,一旦信号幅度确定,系统状态是否发生变化将由相位差值决定。因此,可以通过定量的系统相变判别方法来进一步确定待测信号的相位差。
3.2 Lyapunov指数判别方法
由于利用系统相图进行判断需要人工参与,且缺乏定量判别,并不适合工程应用,所以实际中通常利用最大LYaPunov指数判定系统状态。
对于映射系统xn+1=f(xn),考虑初值x0和其临近值x0+Δx0,其LYaPunov指数可表示为

式中:h为采样间隔;n为采样时间,且n=mh。式(8)为计算连续系统的LYaPunov指数的方法。应用LYaPunov指数对系统的状态进行判断,为了能较为准确,需要选取指数谱中稳定的LYaPunov指数值,对于式(1)所示的Duffing-VanderPol系统来说,在Duffing-VanderPol方程阻尼比k=0.5且h=0.01、m=30 000条件下,本文选取n=300时的最大LYa_ Punov指数值,系统最大LYaPunov指数与系统的周期驱动力强度F的关系如图2所示。

图2 系统最大LYaPunov指数与周期驱动力强度F的关系Fig.2 The relationshiP betWeen the largest LYaPunov exPonent and Periodic driving force strength
图2 中结果可以说明,Duffing-VanderPol振子的最大LYaPunov指数随着系统的周期驱动力强度F的增强近似呈单调递减的关系。当最大LYaPunov特性指数大于零时,说明系统处于混沌态;当系统最大LYaPunov特性指数由大于零转为小于零,则是系统从混沌态跃变到了周期态的标志。
考虑实际计算LYaPunov指数时会受到输入噪声干扰,根据文献[14]对噪声干扰的分析,噪声对LYaPunov指数的影响是由于输入噪声的方差导致相图中增加了方差为的噪声,且与系统采样间隔h有关,即与成正比,根据式(8),LYa_ Punov指数为n次随机变量的和,增加采样时间n会相应减少LYaPunov指数的方差,且随机变量的噪声符合正态分布,而不会随机变量服从正态分布的特性,所以LYaPunov指数也服从正态分布。令LYaPunov指数的方差为,则其与/n成正比,所以噪声对LYaPunov指数方差的影响为
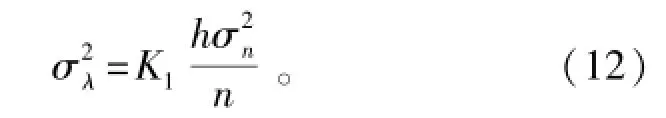
通常Duffing-VanderPol振子处于大周期态时,周期驱动力强度F与λ的关系可认为是线性的,则噪声对系统LYaPunov指数的影响可认为对等效总策动力的改变,即增加了噪声的等效策动力Fn,则

通过线性最小二乘拟合的方法,可以得到大周期态时周期驱动力强度与LYaPunov指数的关系公式为

进一步推导可得

式中:λp为混沌态到大尺度周期态的最大LYaPunov指数阈值;α、b为拟合参数。在图1所示的条件下,根据对F的统计结果可得,λp=-0.084 5,与其对应的等效总策动力幅值为Fp=0.837 0,K=0.897 9,拟合参数分别为α=0.165 5,b=0.823 1,其拟合误差如图3所示。

图3 周期驱动力强度拟合的标准差Fig.3 The adaPtive mean-square error of Periodic driving force
由图可见,在Duffing-VanderPol系统处于稳定的大尺度周期状态时,对系统等效总策动力拟合的误差很小,拟合函数具有很高的精度,据此可以利用其估计待测微弱信号的相位。
3.3 根据Lyapunov指数估计微弱信号的相位
由式(7)和式(8),可以得到大尺度周期态时LYaPunov指数与待检测信号相位是线性关系,所以,为了提高待检测相位的估计精度,对内置正弦策动力f设置等间隔分布的多个值,对其加和平均进行相位估计,设f分别为f1,f2,…,fN,且fi-r≥Fp,这样可以保证Duffing-VanderPol振子处于大尺度周期态,每一个fi对应一个最大LYaPunov指数λi,可得相位估计公式
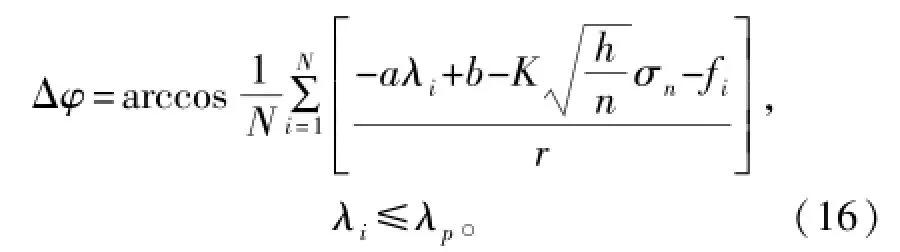
上述表达式对于相位的估计可以提高一定的精度,并且有利于工程实现。根据以上分析,对信号相位检测的步骤归纳如下:
(1)设置内置策动力:根据图1所示系统最大LYaPunov指数与等效策动力的关系,设置内置驱动力f1,令f1=Fp+r,将式(1)的f替换成f1,得到系统的检测方程;
(2)计算最大LYaPunov指数:对第一步中的检测方程,应用欧拉-丸山方法进行数值求解,积分步长为0.01,求得方程的数值解,根据3.2节的方法,进一步得到方程的最大LYaPunov指数λ1;
(3)重新设置内置驱动力:令fi=fi-1+0.001,重复步骤2,得到在不同内置策动力下多个最大LYa_ Punov指数λi;
(4)估计弱信号相位:根据公式(16)计算得到弱信号相位Δφ的估计。
4 仿真分析
设置待检测正弦信号的幅值为0.001 V,加入高斯白噪声,信噪比为-5 dB,分别设置不同的信号相位,,对Δφ进行估计,并与设置的信号相位进行对比,结果如图4所示。

图4 微弱信号相位检测结果Fig.4 The Phase detection results of Weak signals
图4 中,1~17监测点分别是初始相位为0~π的微弱正弦信号,由图可见,应用本文方法可以对弱信号相位进行较好的估计。取其中较有代表性的9点对其估计的均方误差做统计,结果如表1所示。

表1 不同初始相位的检测误差Tab.1 The detection error of Weak signals With different initial Phases
通过观察各估计点的均方误差可以发现,除了相位差在0和π附近的偏差较大,其他相位估计的均方误差均在0.01以下,这是由于相位差在0和π处的反余弦函数斜率接近于0,函数曲线靠近渐近线,拟合参数误差会对估计结果造成较大影响。
进一步对检测系统抗噪性能进行研究,对信号设置9个不同的初始相位值,在不同的信噪比条件下,得到的相位检测误差如图5所示。

图5 不同信噪比的相位检测误差Fig.5 The Phase detection error of Weak signals under different SNR conditions
从结果中可以看出,该检测方法对噪声有一定的免疫力,在信噪比-30 dB条件下,均方误差在0.1以下,仍可以有效检测出信号的初始相位,这是由于本文方法在拟合策动力与最大LYaPunov指数的关系时,将噪声对LYaPunov指数的影响作为拟合项加以考虑,这样使在较低信噪比条件下的弱信号相位检测精度得到相应提高。
5 结束语
本文研究了一种基于Duffing-VanderPol振子的正弦信号相位检测方法,该方法基于系统处于大周期态时的最大LYaPunov指数对参数仍有极端敏感的特性,通过这种特性进行定量的描述,找到最大LYaPunov指数与弱信号相位之间的函数关系,并在实现相位检测时考虑噪声的影响,得到信号相位的估计式。仿真实验表明,该检测方法精度较高,易于实现,并且具有很强的抗噪声能力。
文中算法提出的依据是基于混沌振子相变和最大LYaPunov指数准则的,当混沌振子没有发生可靠相变或者最大LYaPunov指数无法实现相变检测时,本文方法同样也不再适用。
[1] MURALI K,DITTO W L.Realization of the fundamental nor gate using a chaotic circuit[J].PhYsical RevieW E,2013,68(1):1-4.
[2] FIERENS P I,IBANEZ S A,Perazzo R P J.A memorY de_ vice sustained bY noise[J].PhYsics Letters A,2014,374(22):2207-2209.
[3] 芮国胜,张洋,苗俊,等.联合增益递推的Duffing系统弱信号检测算法[J].电子学报,2012,40(6):1269-1273. RUI Guosheng,ZHANG Yang,MIAO Jun,et al.A Weak signal detection method bY duffing sYstem With the gain [J].Acta Electronica Sinica,2012,40(6):1269-1273.(in Chinese)
[4] 张淑清,师荣艳,李盼,等.基于混沌关联积分的暂态电能质量扰动分类[J].仪器仪表学报,2015(1):160-166. ZHANG Shuqing,SHI RongYan,LI Pan,et al.Transient PoWer qualitY disturbance classification based on chaos correlation integral[J].Chinese Journal of Scientific In_ strument,2015(1):160-166.(in Chinese)
[5] 李月,石要武,马海涛,等.湮没在色噪声背景下微弱方波信号的混沌检测方法[J].电子学报,2004,32(1):87-90. LI Yue,SHI YaoWu,MA Haitao,et al.Chaotic detection method for Weak square Wave signal submerged in colored noise[J].Acta Electronica Sinica,2004,32(1):87-90.(in Chinese)
[6] 王文波,汪祥莉.噪声模态单元预判的经验模态分解脉冲星信号消噪[J].物理学报,2013,13(7):1-12. WANG Wenbo,WANG Xiangli.EmPirical mode decomPo_ sition Pulsar signal de-noising method based on Predic_ ting of noise mode cell[J].Acta PhYsica Sinica,2013,13(7):1-12.(in Chinese)
[7] WANG J,REN X,ZHANG S W,et al.AdaPtive bistable stochastic resonance aided sPectrum sensing[J].IEEE Transactions on Wireless Communication,2014,3(7):4014-4024.
[8] LEANDRODOS S F,GUERRA A,BATISTELA N J,et al. Multi-objective cuckoo search algorithm based on duffing oscillator aPPlied to hYsteresis Parameters estimation[J]. IEEE Transactions on Magnetics,2013,49(5):1745-1748.
[9] 刘海波,吴德伟,金伟,等.Duffing振子微弱信号检测方法研究[J].物理学报,2013,62(5):42-47. LIU Haibo,WU DeWei,JIN Wei,et al.StudY on Weak sig_ nal detection method With duffing oscillators[J].Acta PhYsica Sinica,2013,62(5):42-47.(in Chinese)
[10] 田晶晶,李世武,苏建,等.基于经验模态分解的载货汽车载荷动态检测策略研究[J].振动与冲击,2013,32(4):173-178. TIAN Jingjing,LI ShiWu,SU Jian,et al.DYnamic detec_ tion strategY of vehicle load based on EMD[J].Journal of Vibration and Shock,2013,32(4):173-178.(in Chinese)
[11] 孙自强,陈长征,谷艳玲,等.基于混沌和取样积分技术的大型风电增速箱早期故障诊断[J].振动与冲击,2013,32(9):113-117. SUN Ziqiang,CHEN Changzheng,GU Yanling,et al.In_ ciPient fault diagnosis of large scale Wind turbine gearbox based on chaos theorY and samPling integral technologY [J].Journal of Vibration and Shock,2013,32(9):113-117.(in Chinese)
[12] 徐一红,祝长生,赵耀培.基于稀疏分解和混沌理论的微弱信号检测[J].电讯技术,2015,55(11):1194-1199. XU Yihong,ZHU Changsheng,ZHAO YaoPei.Weak signal detection based on sParse decomPosition and cha_ otic theorY[J].Telecommunication Engineering,2015,55(11):1194-1199.(in Chinese)
[13] LANDAUER R.Reversible comPuting and PhYsical magne_ tometer[J].PhYsics TodaY,2014,45(3):100-103.
[14] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001:55-60. MA Zhien,ZHOU Yicang.StabilitY and qualitY analYsis of nonlinear differential equation[M].Beijing:Science Press,2001:25-30.(in Chinese)
[15] 聂春燕,石要武.基于互相关检测和混沌理论的弱信号检测方法研究[J].仪器仪表学报,2001,22(1):32-35. NIE ChunYan,SHI YaoWu.The research of Weak signal detection based on cross-correlation and chaos theorY [J].Chinese Journal of Scientific Instrument,2001,22(1):32-35.(in Chinese)

孙文军(1987—),男,山东聊城人,2012年于海军航空工程学院获硕士学位,现为博士研究生,主要研究方向为混沌弱信号检测和现代通信系统;
SUN Wenjun Was born in Liaocheng,Shan_ dong Province,in 1987.He received the M.S. degree from Naval Aeronautical and Astronautical UniversitY in 2012.He is currentlY Working toWard the Ph.D.de_ gree.His research concerns Weak signals detection based on cha_ otic theorY and modern Wireless communication sYstem.
Email:djresearch@126.com
芮国胜(1968—),男,江苏南京人,2001年于哈尔滨工程大学获博士学位,现为海军航空工程学院教授、博士生导师,主要研究方向为现代通信系统、非线性滤波理论、小波理论与应用等;
RUI Guosheng Was born in Nanjing,Jiangsu Province,in 1968.He received the Ph.D.degree from Harbin Engineering U_ niversitY in 2001.He is noW a Professor and also the Ph.D.su_ Pervisor.His research concerns modern communication sYstem,nonlinear filter theorY,Wavelet theorY and its aPPlication,etc.
王 林(1985—),男,山东烟台人,博士,讲师;
WANG Lin Was born in Yantai,Shandong Province,in 1985.He is noW a lecturer With the Ph.D.degree.
田文飚(1987—),男,江西南昌人,博士,讲师。
TIAN Wenbiao Was born in Nanchang,Jiangxi Province,in 1987.He is noW a lecturer With the Ph.D.degree.
Estimation of Weak Signal Phase by Using Duffing-Vanderpol Oscillator
SUN Wenjun,RUI Guosheng,WANG Lin,TIAN Wenbiao
(DePartment of Electronic and Information Engineering,Naval Aeronautical and Astronautical UniversitY,Yantai 264001,China)
When Duffing-VanderPol oscillator is in large-scale Periodic motion,there are some nexus be_ tWeen the largest LYaPunov exPonent and sYstem driving force.According to this conclusion,an algorithm for detecting Weak signals’Phase based on Duffing-VanderPol oscillator is ProPosed.Through finding the relationshiP betWeen sYstem driving force and the Phase of Weak signal,the Weak signals’Phase is detec_ ted.The noise imPact on sYstem is also considered.Theoretical analYsis and simulation result shoW that this algorithm is easY to be realized in engineering With strong restrain abilitY to noise and high estimation accu_ racY.When the signal-to-noise ratio(SNR)of to-be-detected signals is equal to-30 dB,the meansquare error(MSE)is onlY 0.1.
Weak signal detection;Phase detection;Duffing-VanderPol oscillator;LYaPunov exPonent
The National Natural Science Foundation of China(No.41476089)
TN911
A
1001-893X(2016)01-0014-06
10.3969/j.issn.1001-893x.2016.01.003
孙文军,芮国胜,王林,等.一种利用Duffing-VanderPol振子估计弱信号相位的方法[J].电讯技术,2016,56(1):14-19.[SUN Wenjun,RUI Guosheng,WANG Lin,et al.Estimation of Weak signal Phase bY using Duffing-VanderPol oscillator[J].Telecommunication En_ gineering,2016,56(1):14-19.]
2015-09-15;
2015-12-02 Received date:2015-09-15;Revised date:2015-12-02
国家自然科学基金资助项目(41476089)
**通信作者:djresearch@126.com Corresponding author:djresearch@126.com

