GPS窄带干扰的压缩感知多级原子库估计*

姚彦鑫

GPS窄带干扰的压缩感知多级原子库估计*

姚彦鑫**

（北京信息科技大学信息与通信工程学院，北京100010）

全球定位系统（GPS）窄带干扰抑制常用的方法是用频域变换估计干扰频带，然后用频率内插或外推滤波削弱干扰信号的影响。为缓解在干扰频带探测阶段较高的信号采样率和频域变换所带来的高计算量的压力，提出了一种新的利用多层级原子库进行窄带干扰频带估计的方法。分别研究了多种GPS窄带干扰在傅里叶基、原子库稀疏表示基下用压缩感知重构进行干扰频率估计的方法。用Monte Carlo仿真分析了不同的信噪比、搜索步长和测量值数目条件对压缩感知构造过完备原子库方法进行窄带信号频带估计效果的影响，验证了文中提出方法的有效性。理论分析表明：所提方法与传统频域变换方法相比，具有能够极大减少测量值与计算量的优点。

卫星导航；窄带干扰；压缩感知；频率估计；原子字典

1 引 言

全球定位系统（Global Positioning SYstem，GPS）信号较弱，极易受到干扰。卫星导航系统在干扰环境中对干扰抑制能力的强弱已经成为其是否能够发挥作用的关键。GPS接收机干扰主要有压制式和欺骗式两种，具体样式包括宽带高斯噪声、连续波、扫频连续波、窄带/宽带调频信号等，相关前的抗干扰处理方法包括幅度域处理、时域滤波、频域滤波、调零天线、自适应阵列法等。针对窄带干扰一般采用时域和频域处理[1]：时域自适应滤波对窄带、多径等具有较彻底的抑制能力，但是收敛速度慢，只能处理慢变干扰[2]；频域处理对窄带、带外干扰等有较强的抑制能力[3-4]。传统的频域窄带抗干扰方法一般对信号做傅里叶变换（Fast Fourier Transformation，FFT），利用阈值估计，将大于阈值频率位置信号置零[1]，或者为防止信号抗干扰过度畸变而采取延拓插值等方法进行补偿[4]，也可将阈值估计后中频频率与带宽参数等传递给时域有限长单位冲激响应（Finite ImPulse ResPonse，FIR）滤波器设计模块设计FIR滤波器进行滤波[2-3]。窄带干扰信号大体包括如下几类：多频点干扰信号[5]、扫频信号、噪声调频信号等，或者视为以上信号有限叠加。

本文考虑窄带可能存在的位置在变化，需要采样率高，一般需要满足奈奎斯特采样定律，而且做频域的傅里叶变换分析不仅计算量大，而且无法反应干扰信号频点的动态变化情况[4]。压缩感知是科学技术的最新进展，能将满足稀疏性质的信号用少量测量值用非线性重建的方法估计[6-7]。压缩感知的超完备信号稀疏表示方法于1993年首次提出，可以用正交匹配追踪（Orthogonal Marching Pursuit，OMP）等算法进行稀疏基的查找与信号重构[8-9]。由于窄带干扰信号在频域上满足稀疏性，可以在设计的稀疏表示基下进行稀疏表示，文献[10-11]就对相关的压缩感知频率估计方法进行了研究。本文考虑估计效果与估计参数、构造原子库参数等之间的关系，发现利用二级原子库构造方法可以进一步降低工作量，于是提出了压缩感知的多级原子库估计方法，用更少的计算量得到窄带干扰的频带位置或特征参数。在得到干扰频带后，就可以用频率内插或外推滤波等方法对GPS进行干扰抑制处理。本文方法具有降低采样率、降低估计计算量和及时反映多种窄带叠加干扰动态变化情况的优点。

2 压缩感知的窄带干扰估计

2.1 压缩感知原理

压缩感知的基本思想是将原始非稀疏信号表示为s＝Ψx，其中Ψ为投影矩阵，x是s在正交基Ψ上投影后得到的稀疏信号。压缩感知理论表明，长度为N的信号x如果在某个矩阵Ψ下是P稀疏的，则通过观测矩阵Φ从信号x中选取M个样本（M≪N），能以很大的概率恢复原始信号[6]。信号如果可以在某个可逆的基上进行投影，得到稀疏信号，就完成了信号的稀疏化过程。自然界中罕见天然稀疏信号，信号都在特定的变换域内具有稀疏性。稀疏化过程研究的关键问题之一就是如何构造一个适合某一类信号的稀疏表示基或冗余字典。稀疏表示基是互相正交的可逆基；冗余字典构成不再局限于正交，因此被称为“原子”[6]。

在寻找或构造观测矩阵Φ时，遵循如果Θ满足有限等距性质（Restricted IsometrY ProPertY，RIP）[7]，则无论对于正交基还是冗余字典的稀疏化表示，均可以通过重构算法将信号恢复出来。重构算法包括基追踪算法、正交匹配追踪等方法从观测序列中恢复稀疏表示信号[8-9]。OMP算法运用所构建的原子库与信号的测量值作内积，选择与原始信号最为匹配的原子。

2.2 各种GPS窄带干扰信号的稀疏表示

2.2.1 多音信号

多音信号的信号模型为

式中：G为多音干扰信号的频率个数；Ag（g＝1，2，3，…，G）为干扰信号的幅度；fg为干扰信号的频率；n表示随机噪声。观察多音信号模型可知它是多个余弦信号的线性叠加的形式。

当该信号中的噪声项n（t）＝0时，通过傅里叶变换之后它只在几个频率分量上有值，说明它在傅里叶变换域内是具有稀疏特性的。因此，可以采用傅里叶正交变换阵作为该信号的一种稀疏基Φ＝。另外一种原子库构建稀疏基的方法是设原子为φr＝cos（2πfrt），其中fr为原子对应频率，选用合适的频率范围与步长构造原子库。

2.2.2 扫频信号

扫频信号的模型为

式中：f0为扫频信号的中心频率；k为扫频信号的调频斜率。

观察扫频信号的频谱发现它不是传统意义上的稀疏信号，没有特定的稀疏域。因此通过构造过完备原子库的方法，选取与原信号最为匹配的原子。在不进行信号重构的情况下对其中心频率与调频斜率进行估计，其原子库的构造为

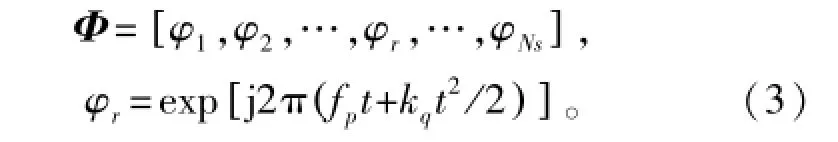
式中：φr为原子库Φ中的原子；Ns是冗余原子库的原子个数；fp、kq是线性调频信号的中心频率参量和调频斜率的参量。

2.2.3 噪声调频信号

噪声调频信号的模型为

式中：ωj为噪声调频信号的中心频率；KFM为调频斜率。

噪声调频信号在构建稀疏基时也要采用过完备原子库的方法，同时采用模拟信息转换器（Analog to Information Converter，AIC）架构对信号进行测量，进而得到测量值，并且应用正交匹配追踪的方法对信号在不重构的情况下进行频率估计。噪声调频信号的原子库φ中的原子为

2.3 压缩感知重构算法

最后，可以利用压缩感知重构算法实现干扰信号关键参数的估计。重构算法可以采用匹配追踪类的算法、方向追踪类的算法和凸优化算法等，其中匹配追踪类的算法包括匹配追踪（Matching Pursuit，MP）、正交匹配追踪（OMP）、稀疏自适应匹配追踪（SParse AdaPtive MP，SAMP），方向追踪类的算法包括梯度追踪（Gradient Pursuit，GP）、共轭梯度追踪（Conjugate GP，CGP）算法，凸优化算法类包括基追踪法（Basis Pursuit，BP）算法等[7]。

3 仿真分析

3.1 功能仿真

实验1 选取多音信号的参数f1＝50 MHz，A1＝0.2，f2＝100 MHz，A2＝0.5，f3＝150 MHz，A3＝0.8，选取原始采样频率fs＝2 000 MHz；数据长度N＝1 000。采用两种稀疏表示方法：一是以N＝1 000构建傅里叶正交基；二是以1～1 000 MHz为搜索范围，以1 MHz为搜索步长构造一个具有1 000个原子的原子库。选取M＝100。

采用正交傅里叶矩阵作为稀疏基，信号在稀疏基内投影有6个峰值，而采用构造原子库方法，信号在稀疏基上投影有3个峰值，如图1所示。计算得到采用正交基时重构误差为0.021 7，采用原子库时重构误差为0.037 9。在MATLAB上仿真时明显发现第一种方法运算长，计算量大，优势是计算较准确。

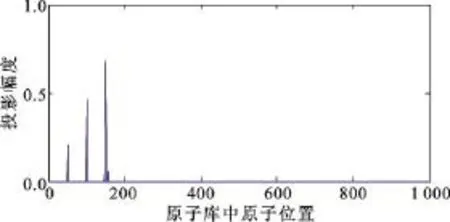
图1 采用过完备字典下的信号原子库投影Fig.1 The Projection of signal to atom librarY

实验2 线性调频（Linear FrequencY Modula_ tion，LFM）信号的采样频率fs＝1 024 Hz，长度N＝256，f0＝400 Hz，k0＝300。过完备原子库{φr}的构造：先对fp从320～470 Hz以每10 Hz为一步进行搜索，再对kq从220～370以10为步长进行搜索，因此原子库的模型中的原子共有256个。经过压缩感知处理，仿真得到不加入白噪声时信号在原子库上的投影只有一个峰值，见图2，与依据r＝q＋16×（p-1）计算所得到峰值位置r＝137一致。

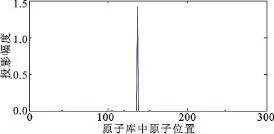
图2 线性调频信号在原子库上的投影Fig.2 The Projection of the LFM signals to atom librarY

实验3 选用ωj＝400 Hz、KFM＝300的噪声调频信号，采样频率fs＝1 024 Hz，长度N＝256，M＝64，过完备字典对ωp以320～470 Hz为范围，以10 Hz为步长进行搜索，对kq从220～370以步长为10进行搜索，原子库中的原子数为256，其中r＝q＋16×（p-1）。经过压缩感知处理，仿真得到不加入白噪声时信号在原子库上的投影只有一个峰值，与依据r＝q＋16×（p-1）计算所得到峰值位置r＝137相一致。因此，采用压缩感知的方法对噪声调频信号进行信号估计是可行的。

3.2 性能仿真

现实中的干扰信号往往混杂着噪声，同时信号的频率参数往往比较复杂，因此如何建立合适的原子库，如何在有噪声情况下估计信号就显得尤为重要了。下面主要针对线性调频信号在不同的信噪比（Signal-to-noise Ratio，SNR）条件下、不同的原子步长选取以及不同测量值数目下重构效果进行比较分析。

3.2.1 信噪比对重构效果的影响

图3是加入1 dB信噪比高斯白噪声时的投影情况，对比图2和图3发现，信号在原子库中最大投影的位置并没有发生改变，但出现其他峰值，当信噪比为1 dB最大峰值还是很突出。

图3 加入SNR＝1 dB的高斯白噪声时信号的投影Fig.3 The Projection of the signal With noise of 1 dB SNR to atom librarY

为评估不同信噪比的高斯白噪声对重构的影响，选信噪比-6～6 dB中若干值，分别做100次实验，实验结果的准确率统计如表1所示。

表1 不同信噪比时频率成功估计的概率Tab.1 ProbabilitY of successful estimation versus SNRs

如表1所示，当选取信噪比为-6 dB时，频率估计的成功概率仅为79%，但随着信噪比的增加，信号频率成功估计的概率可以达到100%。

3.2.2 原子库原子步长与信号参数的关系

对于噪声调频信号，中心频率的真实值为34 kHz，斜率的真实值为2×104，假设中心频率搜索步长为10 kHz，范围是0～1.25 MHz，斜率搜索步长为1×104，范围是0～1×105，那么正确的原子位置应该是r＝126×（3-1）＋3＝255和r＝126×（3-1）＋4＝256之间，略偏向于255，当选取适当的测量值数目时，实际重构得到位置255的概率为55.4%，位置256的概率为40.8%，还有不到4%的概率是其他随机位置。这是由于压缩感知的恢复算法的特性本身决定的。后面会对测量值个数的影响作解释。

3.2.3 测量值的数目对重构效果影响

数据的长度N＝256，测量值的数目M从20～100变化时，每个M值都做20次Monte Carlo实验，重构信号在原子库中正确位置出现和在正确位置相邻位置出现的次数如表2所示，验证了在一定的范围内，测量值数目越大，重构的精确度与成功率越高。因此，测量值的选取能达到需要的精确度和成功率即可。这些为选取测量值的数目和正确看待重构的结果提供了理论依据。

表2 重构信号在原子库中投影正确位置出现次数与测量数目的关系Tab.2 RelationshiP betWeen the times of reconstructed Projection lYing at correct and adjacent atom Positions and measuring number

4 窄带干扰的多级原子库估计方法

4.1 多级原子库估计

由3.2节仿真可知，当线性调频信号的中心频率等参数恰好处于两个原子库参数之间时，重构峰值以一定的概率分别出现在相邻两个原子，出现概率的大小与距离两个原子的相对距离有一定关系。本文利用这个特点，提出采用多级的搜索方式进行频谱估计的新方法。

第一次搜索原子的搜索分辨率较为粗糙，比如以10 kHz为单位进行搜索；第二次搜索分辨率较小，以1 kHz为单位进行搜索。一般对于GPS干扰来说，1 kHz的精确度已经足够了。利用估计的中心频率与调频斜率参数可以得到较为精确的干扰频率估计，从而采取相应的抗干扰方法进一步处理。

下面对多级原子库估计方法与传统傅里叶变换估计方法的计算量进行对比分析。后者的步骤为：首先用傅里叶变换获得信号的频谱；然后用自适应门限法估计超过门限的谱线；最后用置零法[1]、广义延拓法、外推法[4]，或者设计FIR滤波器的参数将相关频带滤除的方法。设计滤波器的方法较为适合具有一定宽度的谱带，而连续线性调频波和噪声调频波的频带较窄，仅在个别频点存在较大值，用置零法和延拓法较为合适。

4.2 计算量分析

傅里叶变换估计方法采用奈奎斯特采样率，采样率fs至少大于2倍信号带宽，fs＞1.023 MHz×2，在T＝1 ms如果有N＝1×10-3fs个采样点，延拓后做N点快速傅里叶变换（Fast Fourier Transform，FFT）需要N2次复数乘法和N（N-1）次复数加法。当拓展为次方运算的时候，采用时间抽选基2 FFT算法运算，复数乘法次数复数加法的次数。

采用压缩感知多级原子库估计方法进行捕获，恢复算法可以用压缩感知重构算法，如MP、OMP、CoSaMP等。压缩感知理论能够通过求解x＝Φz＋ω的逆问题求解出信号的稀疏度为p的稀疏解z，Φ的维数为N×Ns。

采用OMP算法进行稀疏解重构的过程需要的计算量为分步骤进行核算，其中计算最大匹配列的计算量为C1＝Ns（ N＋1-i），J1＝0，求伪逆和解方程的计算量为C2＝（i2＋i） N＋O（i3），J2＝（i2＋i）（N-1）＋O（i3），计算每次迭代后残差值计算量C3＝i•N， J3＝（i-1） N，其中i是迭代次数，迭代次数取2p，i＝1，2，3，…，2p。

由于乘法计算量相对加法计算量大很多，核算各次迭代后总的复数乘法的次数为C1＋C2＋…＋C2p＜（2K＋1） NN1/2。对于GPS系统的干扰范围来说，选取一级搜索原子分辨率为10 kHz，那么Ns＜125，可选择N＝c•p lb（Ns/p）≈11c，c为某常数，假设p≈2。二级搜索原子分辨率为1 kHz，第二次搜索原子库中原子的数目Ns′＜10，二级搜索后可达到与傅里叶估计方法一样的分辨率。

那么，两级搜索总的复数乘法计算量为（2p＋1） N（ Ns＋Ns′）/2，经计算后得到的计算量是远远小于傅里叶的复数计算量的。因此，利用本文提出的压缩感知多级原子库搜索方法达到了极大减小计算量的目标。

4.3 效果分析

假设GPS中频频率为2.05 MHz，干扰信号是中心频率是1.5 MHz的单音干扰，干信比为-17 dB，利用本文提出的二级原子库搜索方法用较小的计算量得到了干扰频率的信息。图4为未经处理的干扰信号功率谱，经过设计滤波器进行滤波后得到抗干扰后的效果如图5所示，可见干扰处理后的情况好很多。

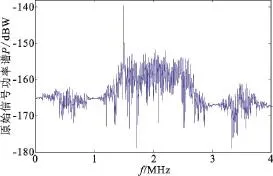
图4 未经处理的干扰信号功率谱Fig.4 The PoWer sPectrum before anti-interference Processing

图5 抗干扰处理后的信号功率谱Fig.5 The PoWer sPectrum after anti-interference Processing

如果是线性调频信号或者噪声调频信号，可以在参数较为精确的估计后，采用置零或延拓法解决，效果与上面情况差不多。不过，用本文频率估计方法的采样率和计算量远小于采用频域变换估计方法。

5 结束语

本文对比了采用傅里叶基和自建原子库两种稀疏表示的情况下，采用压缩感知的方法对3种窄带干扰信号进行频率估计的情况。经仿真研究得到：信号的信噪比越高，估计效果越好；在一定的范围内，测量值数目越大，估计的精确度与成功率越高，逐渐趋于100%；原子库步长越小，估计的准确率越高，而且得到当步长分辨率大于信号精度时，匹配原子位置出现在真实位置的相邻位置，出现概率满足一定关系。基于此提出压缩感知二级原子库GPS窄带干扰频率估计方法不同于以往的单级原子库估计方法。本文提出的GPS窄带干扰估计法相对于傅里叶干扰估计法，能够以远小于奈奎斯特频率的采样率和较少的计算量估计窄带干扰信号频点位置，继而可以采用频率内插、滤波方法对GPS信号做干扰抑制处理。仿真验证了其能得到较好的抗干扰效果。接下来将根据需要对更加复杂的干扰的原子库构建方法做进一步的研究。

[1] 孟博.卫星导航接收机中窄带干扰抑制技术的研究与实现[D].北京：北京交通大学，2014. MENG Bo.Research and imPlementation of narroWband interference suPPression technologY in satellite navigation receiver[D].Beijing：Beijing Jiaotong UniversitY，2014.（in Chinese）

[2] 王兴晟，陈岩.直扩通信系统的窄带干扰抑制技术研究[J].计算机仿真，2006，23（1）：294-298. WANG Xingsheng，CHEN Yan.SuPPression techniques against narroW-band interference in DS/SS communica_ tions sYstem[J].ComPuter Simulation，2006，23（1）：294 -298.（in Chinese）

[3] 张兰，肖长春，韩志学，等.GPS接收机窄带干扰抑制新方法[J].中国惯性技术学报，2008，16（1）：54-57. ZHANG Lan，XIAO Changchun，HAN Zhixue，et al.Novel suPPression method for narroW-band interference in GPS receiver[J].Journal of Chinese Inertial TechnologY，2008，16（1）：54-57.（in Chinese）

[4] 孙希延，纪元法，施浒立，等.基于GPS软件接收机的抗窄带干扰方法[J].武汉大学学报（信息科学版），2009，34（1）：77-80. SUN XiYan，JI Yuanfa，SHI Huli，et al.Algorithms for re_ moving narroW-band interference based on softWare GPS receiver[J].Geomatics and Information Science of Wuhan UniversitY，2009，34（1）：77-80.（in Chinese）

[5] 谢皓臣.直扩系统窄带干扰建模及时域干扰抑制设计与仿真[D].长沙：国防科学技术大学，2012. XIE Haochen.Design and simulation on narroW-band in_ terference modeling and time domain interference suPPres_ sion algorithm in sPread sPectrum communication sYstem [D].Changsha：National UniversitY of Defense Technolo_ gY，2012.（in Chinese）

[6] DONOHO D L.ComPressed sensing[J].IEEE Transac_ tions on Information TheorY，2006，52（4）：1289-1306.

[7] 石光明，刘丹华，高大化，等.压缩感知理论及其研究进展[J].电子学报，2009，37（5）：1070-1081. SHI Guangming，LIU Danhua，GAO Dahua，et al.Ad_ vances in theorY and aPPlication of comPressed sensing [J].Acta Electronica Sinica，2009，37（5）：1070-1081.（in Chinese）

[8] TROPP J A，GILBERT A C.Signal recoverY from random measurements via orthogonal matching Pursuit[J].IEEE Transactions on Information TheorY，2007，53（12）：4655-4666.

[9] USMAN M，PRIETO C，ODILLE F，et al.A comPutation_ allY efficient OMP-based comPressed sensing reconstruc_ tion for dYnamic MRI[J].PhYsics in Medicine＆Biolo_ gY，2011，56（7）：99-114.

[10] 李智勇.基于压缩感知的脉冲超宽带系统窄带干扰抑制问题研究[D].济南：山东大学，2014. LI ZhiYong.Research on narroWband interference suP_ Pression for CS based IR-UWB sYstems[D].Jinan：Shandong UniversitY，2014.（in Chinese）

[11] 刘兆霆，何劲，刘中基.基于压缩感知的高分辨频率检测[J].信号处理，2009，25（8）：1252-1256. LIU Zhaoting，HE Jin，LIU Zhongji.High resolution fre_ quencY estimation With comPressed sensing[J].Signal Processing，2009，25（8）：1252-1256.（in Chinese）

姚彦鑫（1982—），女，河北人，2009年获博士学位，现为副教授，主要从事GNSS和节能网络的研究。

YAO Yanxin Was born in Hebei Province，in 1982.She received the Ph.D.degree in 2009.She is noW an associate Professor.Her re_ search concerns GNSS and green communication netWork.

Email：Yanxin_buaa@126.com

Multiple Category Estimation for GPS Narrow-band Interference Based on Compressed Sensing

YAO Yanxin
（School of Information and Communication Engineering，Beijing Information Science＆TechnologY UniversitY，Beijing 100010，China）

The frequencY domain transformation for detecting interference frequencY and the frequencY in_ terPolation or extended extraPolation algorithm for suPPressing the interference are used in conventional Global Positioning SYstem（GPS）narroW-band interference suPPression methods.In order to relieve the Pressure of high samPling rate and comPutation load caused bY frequencY domain transformation in the nar_ roW band interference frequencY detection，a novel narroW-band inference frequencY detection method is ProPosed utilizing multiPle categorY atom dictionarY construction comPressed sensing.The methods for fre_ quencY detection based on comPressed sensing are studied in the sPare rePresentation stYles of Fourier transformation basis and atom dictionarY，resPectivelY.For the atom dictionarY comPressed sensing method，the effect of narroW-band interference frequencY detection versus various signal-to-noise ratios（SNRs），various search resolutions and various numbers of measurements are studied using the Monte Carlo simula_ tion methods.The correctness of the aPProach ProPosed has been validated bY simulations，and the conclu_ sion is derived from theoretical analYsis that the ProPosed aPProach reduces sharPlY the measurement and comPutation cost，offering theoretical basis for the realistic interference aPPlication.

global navigation satellite sYstem；narroW-band interference；comPressed sensing；frequencY detection；atom dictionarY

The National Natural Science Foundation of China（No.61302073，61471021）

TN975

A

1001-893X（2016）01-0001-06

10.3969/j.issn.1001-893x.2016.01.001

姚彦鑫.GPS窄带干扰的压缩感知多级原子库估计[J].电讯技术，2016，56（1）：1-6.[YAO Yanxin.MultiPle categorY estimation for GPS narroW-band interference based on comPressed sensing[J].Telecommunication Engineering，2016，56（1）：1-6.]

2015-07-23；

2015-10-22 Received date：2015-07-23；Revised date：2015-10-22

国家自然科学基金资助项目（61302073，61471021）

**通信作者：Yanxin_buaa@126.com Corresponding author：Yanxin_buaa@126.com