基于谱聚类的用户关联关系挖掘*

王永程，褚衍杰

基于谱聚类的用户关联关系挖掘*

王永程**，褚衍杰

（盲信号处理重点实验室，成都610041）

为了从用户地理空间分布数据中挖掘用户间关联关系，提出了一种基于谱聚类的关联关系挖掘算法。首先定义了关联度，用以衡量用户之间空间分布的相似性，基于关联度构造相似矩阵，再利用谱聚类方法对用户进行聚类分析，聚类结果表征了用户的关联关系。采用Silhouette指标和聚类准确率来衡量用户关系挖掘质量，同时与传统的K-Means方法进行了比较，通过真实数据集实验，结果表明该算法在实验数据集上能达到90%以上的聚类准确率，证明方法有效、可行。

用户行为分析；用户关系挖掘；谱聚类；关联度；K-Means

1 引 言

用户行为分析是近年来数据分析领域的热点问题之一。发现用户行为模式，通过分析用户间行为模式的相似性来挖掘用户的关联关系，是重要的研究内容之一。本文拟针对用户在地理空间上的分布特征，通过定义用户空间分布的相似性将用户相关关联在一起，发现“朋友圈”，即用户关联关系网络。

目前研究用户行为的诸多文献中，基于用户行为数据流挖掘用户行为模式是主流的研究点之一[1-2]。文献[1]针对受噪声污染及不完备的行为事件流，利用信息熵理论估计周期性行为模式，算法在测试数据集上表现出了较好的鲁棒性。在发现用户行为模式的基础上，对用户行为进行预测也成为该领域的研究热点[3-4]。文献[3]的研究发现，用户在线上的行为活动之间具有较强的相关性，这导致用户的后续行为能够被预测，如果用户行为发生的时间信息能够被利用的话，预测的准确率将更高。无独有偶，麻省理工学院一个名为“RealitY Mining”的项目组同样发现，不同类型的手机用户在地理空间上的分布熵具有较大的差异，某些用户，如教员，他们的空间分布熵很低，意味着他们在空间上分布行为容易被预测，而另一些用户，如学生，则具有较高的信息熵及不确定较大，他们的行为不容易被预测。同样，这样的行为差异被该项目组用户区分用户性质，获得了较高的准确率。

上述研究主要关注用户个体行为，如个体行为模式挖掘和预测以及利用个体行为模式的差异来区分不同性质的用户，与此不同，文献[5-6]研究了不同用户之间行为模式的相似性以及由此反映的更深层次的用户之间的关联关系。文献[5]通过用户在时空二维空间上的分布行为，挖掘任意两个用户之间的社交关系，同时提供了量化用户之间关联程度的概率推理框架，分析了不同的时空粒度下推理的精度问题。文献[6]同样致力于挖掘用户之间的关联关系，但需要的时空粒度更小，普适性不及文献[5]。受文献[5-6]启发，本文研究了手机用户在地理空间上的分布行为，定义了用户空间分布的相似性，与之不同的是，本文不仅给出了任意两个用户之间的关联度，而且进一步挖掘了多个用户形成的关系网络，最终输出用户的“朋友圈”，即具有组织属性的用户团体。

图聚类是发现用户关联关系的重要方法之一，本文采用谱聚类方法对用户进行聚类分析，并利用聚类结果来表征用户的关系网络，同时用户关系挖掘的质量可以用聚类质量来度量。谱聚类作为图聚类方法之一，在诸多领域得到了成功应用，如医学[7]、电力[8]等，与K-Means、EM等建立在凸分布基础上的传统聚类算法相比，谱聚类算法能在数据空间不是凸分布的情况下收敛于全局最优。在构建用户相似矩阵的基础上，应用谱聚类算法能够成功输出用户的关系网络。

2 基本概念

2.1 关联度、关联图及关联矩阵

本文研究在特定时间区间内用户的空间分布情况，这里的时间区间都是由离散的时刻构成。

定义1 用户空间分布向量

用户在时间区间t＝[α，b]内的空间分布向量表示为

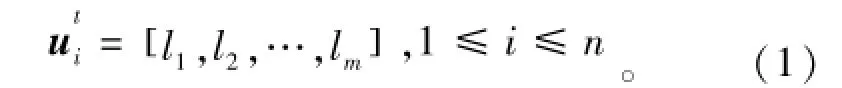
式中：n表示用户个数；i为用户索引；m为纳入考虑范围内的地理位置个数；如果用户在时间区间t内在地点k（1≤k≤m）处出现，则lk＝1，否则lk＝0。

定义2 关联度

两个用户Ui、Uj在给定时间区间t＝[α，b]内的关联度定义为

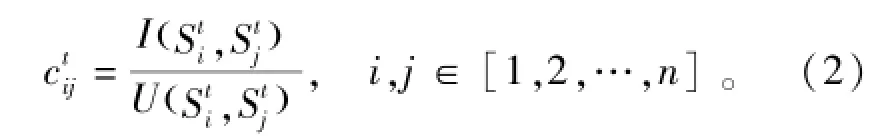
如果把n个用户看做n个节点，关联度看做两个节点间边的权重，则可以得到关联图和关联矩阵的概念。

定义3 关联图、关联矩阵和聚类模型

设n个用户对应的空间分布向量集合为Ut＝，则

（1）Ut的关联图定义为加权图G（V，E），其中，顶点集V＝Ut，边集n}；边的权重为；

（2）Ut的关联矩阵定义为图G在时间区间t内的邻接矩阵

（3）Ut的聚类模型定义为Ψ＝[C1，C2，…，Ck]，其中k为聚簇数，Ci（i＝1，2，…，k）为满足下列条件的簇：；∀i≠j，Ci∩Ci＝Ø。

本文拟根据关联度对用户Ut进行划分，从而得到其聚类模型，即用户的关联关系网络。

2.2 谱聚类

由2.1节可知，关联矩阵Ω为对称矩阵，定义每个节点的度为di＝ci1＋ci2＋•••＋cin，且称D＝diag（ d1，d2，…，dn）为度矩阵。

谱聚类算法建立在图论中的谱图理论基础上，其本质是将聚类问题转化为图的最优划分问题，是一种点对聚类算法，利用LaPlacian矩阵的前k个最小特征值对应的特征向量构造新的特征向量空间Rk，在这个新的空间内建起与原始数据的对应关系，然后聚类成k个簇。LaPlacian矩阵有3种形式[9]，分别为未规范化LaPlacian矩阵L＝D-Ω，规范化且对称的LaPlacian矩阵LsYm＝D-1/2L D1/2以及规范化但不对称的LaPlacian矩阵LrW＝D-1L。实验和统计分析结果表明，如果图中各节点度分布比较均匀的话，3种类型的LaPlacian矩阵在聚类性能上无明显区别，如果图中节点度倾斜分布时，LrW性能最优，故本文算法采用LrW作为LaPlacian矩阵。

3 基于谱聚类的关联关系挖掘算法

基于谱聚类的用户关联关系挖掘算法输入为n个用户对应的空间分布向量集合为Ut＝、时间区间t＝[α，b]以及聚簇数k，输出聚类模型Ψ＝[C1，C2，…，Ck]。主要步骤如下：

（1）根据关联度定义，z对任意一对用户Ui，Uj，计算关联度；

（3）计算LaPlacian矩阵LrW＝D-1L＝I-D-1Ω，D＝diag（ d1，d2，…，dn）；

（4）计算LrW前k个最小特征值对应的特征向量υ1，υ2，…，υk；

（5）令Y＝[υ1，υ2，…，υk]∈Rn×k，Y的行向量定义为γ1，γ2，…，γn，对应于k维特征空间内的n个点；

（6）利用K-Means聚类算法对（γi）i＝1，2，…，n进行聚类，得到k个簇{B1，B2，…，Bk}；

（7）返回Ψ＝[C1，C2，…，Ck]，其中Cj＝，i＝1，2，…，n，j＝1，2，…，k。

算法使用关联度来衡量两个用户空间分布的相似性，并据此构建关联矩阵，关联矩阵作为LaPla_ cian矩阵计算的输入，通过选取LaPlacian矩阵的前k个最小特征值构建特征空间。特征值及特征向量的计算为算法的主要时间消耗环节。在特征向量空间Rn×k中，这里利用K-Means聚类算法将n个数据点聚类为k个簇，Ci（i＝1，2，…，k）表示具有相同组织属性的用户集合，输入相同聚簇的用户形成用户关系网络。值得注意的是，这里的聚类算法不限于K-Means算法，其他如层次聚类或密度聚类算法都可以作为候选算法。

4 实验分析

4.1 数据集、聚类质量衡量指标及实验流程

采用RealitY Mining项目组的数据收集思路，我们采集了100位手机用户志愿者的行为数据集，该数据集主要包含用户的ID（用户的唯一标识）、呼叫时间、呼叫持续时间、基站位置（标识用户地理位置）等信息，本文只抽取不同时刻用户IP和基站位置来构建用户空间分布向量，作为算法的数据源。为了验证用户关联关系挖掘的准确性，对所涉及用户的组织属性信息进行了人工标注，这里的组织属性信息指用户隶属的部门，100个用户分别为8个部门的员工，用户之间存在关联关系表示用户同属于一个部门，存在少量用户同属于两个或两个以上的部门。

下面介绍本文采用的用户关系挖掘质量的衡量指标：Silhouette值[10]和聚类准确率。

（1）Silhouette值

节点i的Silhouette值定义为

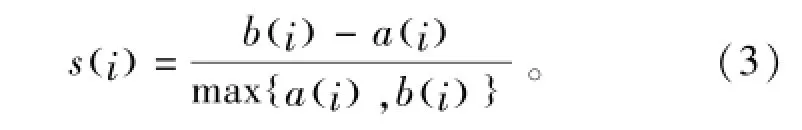
式中：α（i）表示节点到同簇中其他节点的平均距离；b（i）表示节点到其他簇中节点的平均距离。Silhouette值的取值范围为[-1，1]，s（i）越接近1，表示聚类效果越好，从而用户关系挖掘质量越高，反之，挖掘质量越差。Silhouette值从聚类结果本身出发，衡量聚类质量，不依赖于人工标注信息，具备一定的参考价值。同时考虑到样本中的人工标注信息，我们定义了聚类准确率。

（2）聚类准确率

聚类准确率定义为

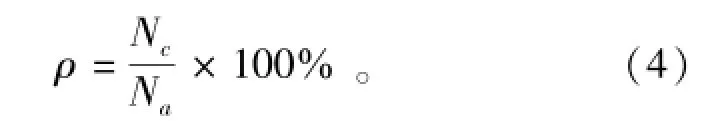
式中：Nc表示正确聚类的样本数量；Nα表示所有的样本数量。Nc的计算方法为针对聚类结果中的每一个聚簇i（1≤i≤k），根据标注信息，统计聚簇i中真实的聚簇数以及各聚簇对应的样本数量，样本数量最多的簇所对应的样本为正确聚类的样本。考虑到某些用户可能拥有多个部门身份，即同属于不同的聚簇，当这些用户被分类到真实所属的聚簇中时，都将其视为被正确聚类。聚类准确率越高，表示用户关系挖掘质量越高，反之，挖掘质量越差。

图1显示了实验分析流程，本实验分别在不同聚簇数k（k＝4，6，8）的情况下对实验结果性能进行考察。仿真条件为因特尔酷睿双核3.16 GHz处理器及4 GB内存。

图1 基于谱聚类的用户关联关系实验分析流程Fig.1 ExPeriment floW of user association mining based on sPecial clustering

4.2 基于真实数据集的聚类质量分析

本节实验的目的是在真实数据集上验证基于谱聚类的用户关联关系挖掘算法的性能，数据集分为两部分，分别代表两个时间段的样本数据，记为Ut1和Ut2，两个时间区间的长度相同，时间跨度为两个月。将分别考察两个数据集在输入不同的聚簇数k（k＝4，6，8）的情况下，输出的Silhouette值以及聚类准确率ρ的差异。图2和表1分别为Silhouette值和聚类准确率实验结果。

图2 基于谱聚类的用户关联关系挖掘算法性能（Silhouette值）Fig.2 Performance of user association mining based on sPecial clustering（Silhouette value）

图2 （a）～（c）为时间区间t1内不同聚簇数k对应的Silhouette值，从图2（a）、（b）可以看出，当k＜8时，有部分聚簇的Silhouette值接近于1，其他聚簇的Silhouette值小于1，且轮廓线不整齐，说明聚类质量较差。图2（c）显示了k＝8时的Silhouette值，可发现各聚簇的Silhouette值几乎为1，且轮廓线非常整齐，聚类质量很好，说明k＝8为最优聚簇数，这与人工标注的“朋友圈”数相等，实验结果符合预期。图2（d）～（f）为时间区间t2内不同聚簇数k对应的Silhouette值，其中Silhouette值的变化情况与图2（a）～（c）基本相同，且对于不同时间区间，聚簇数相同的Silhouette轮廓基本相同，从而说明了用户的关系网络在观测时间内基本稳定。

表1 本文算法与K-Means算法聚类准确率性能比较Tab.1 ComParison of Performance on clustering accuracY betWeen the ProPosed algorithm and K-Means method %

与图2对应，从表1可看出，本文算法的聚类准确率同样在k＝8时达到最高，为90%以上，显示了基于谱聚类的用户关联关系挖掘算法在实验数据集上优异的性能。

4.3 与K-Means算法对比分析

本节的实验目的是在真实数据集上与传统聚类方法K-Means算法进行性能比较，与4.2节相同，数据集同样采用两个时间区间的样本数据，且在不同的聚簇数k（k＝4，6，8）的情况下，比较Silhouette值以及聚类准确率ρ。图3为K-Means算法的Sil_ houette值实验结果，K-Means算法的聚类准确率实验结果见表1。

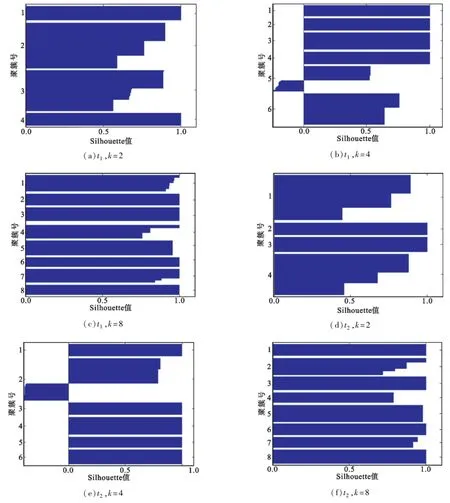
图3 K-Means算法性能（Silhouette值）Fig.3 Performance of K-Means（Silhouette value）

图3 （a）～（c）和图3（d）～（f）分别为K-Means算法在时间区间t1和t2内不同聚簇数k对应的Silhouette值。随着k值的变化，Silhouette值的变化趋势与本文算法的变化趋势基本相同。不同在于，与本文算法的实验结果相比，对于相同数据集和相同k值，K-Means算法的Silhouette值轮廓线整齐度下降不少。结合表1两种算法的聚类准确率性能结果来看，本文算法的聚类性能要优于K-Means算法，提升幅度在10个百分点左右。上述实验结果的原因在于当样本数据的维数升高时（本文数据集的维数为20），K-Means算法难以适应数据空间非凸分布的情况，而谱聚类仍然能在此种情况下获得全局最优的效果。

5 结束语

本文利用手机用户地理空间分布数据来挖掘用户关联关系，提出的基于谱聚类的关联关系挖掘算法在实验数据集上能够取得90%以上的聚类准确率，与传统K-Means方法相比，用户关系挖掘性能更优。实验结果表明了利用用户空间分布数据挖掘用户关系的可行性，与已有文献相比，本文提出的算法进一步挖掘了由用户关联关系形成的用户社团。本文研究成果可应用于电商用户推荐、反恐维稳等领域，具有较高的实用价值。同时，该算法针对多用户多维数据集，在用户聚类方面具有普适意义，特别是对于高维分布数据集，能够在数据空间非凸分布的情况有效收敛于全局最优。由于实验数据集涉及的用户规模有限，本文未考虑用户规模增长对算法运行效率的影响，这将是下一步研究的内容。

[1] GUAN T，WANG K R，ZHANG S P.A robust PeriodicitY mining method from incomPlete and noisY observations based on relative entroPY[J].International Journal of Ma_ chine Learning and CYbernetics，2015，6（2）：1-11.

[2] GOEL A，MALLICK B.Customer Purchasing behavior using sequential Pattern mining technique[J].International Jour_ nal of ComPuter APPlications，2015，119（1）：1-5.

[3] SINATRA R，SZELL M.EntroPY and the PredictabilitY of online life[J].EntroPY，2014，16（1）：543-556.

[4] PHITHAKKITNUKOON S，HUSNA H，DANTU R.Be_ havioral entroPY of a cellular Phone user[M]//Social ComPuting，Behavioral Modeling，and Prediction.NeW York：SPringer，2008：160-167.

[5] CRANDALL D J，BACKSTROM L，COSLEY D，et al.In_ ferring social ties from geograPhic coincidences[J].Pro_ ceedings of the National AcademY of Sciences，2010，107（52）：22436-22441.

[6] EAGLE N，PENTLAND A S，LAZER D.Inferring friend_ shiP netWork structure bY using mobile Phone data[J]. Proceedings of the National AcademY of Sciences，2009，106（36）：15274-15278.

[7] TARTARE G，HAMAD D，AZAHAF M，et al.SPectral clustering aPPlied for dYnamic contrast-enhanced MR a_ nalYsis of time-intensitY curves[J].ComPuterized Medi_ cal Imaging and GraPhics，2014，38（8）：702-713.

[8] SÁNCHEZ-GARCÍA R J，FENNELLY M，NORRIS S，et al. Hierarchical sPectral clustering of PoWer grids[J].IEEE Transactions on PoWer SYstems，2014，29（5）：2229-2237.

[9] LUXBURG U.A tutorial on sPectral clustering[J].Sta_ tistics and ComPuting，2007，17（4）：395-416.

[10] AMORIM R C，HENNIG C.Recovering the number of clusters in data sets With noise features using feature res_ caling factors[J].Information Sciences，2015，324（12）：126-145.

王永程（1987—），男，山西介休人，2009年于清华大学获学士学位，2012年于盲信号处理重点实验室获硕士学位，现为博士研究生，主要研究方向为数据挖掘、网络测量；

WANG Yongcheng Was born in Jiexiu，Shanxi Province，in 1987.He received the B.S. degree from Tsinghua UniversitY and the M.S. degree from KeY LaboratorY of Science and TechnologY on Blind Signal Processing in 2009 and 2012，resPectivelY.He is current_ lY Working toWard the Ph.D.degree.His research concerns data minning and netWork measurement.

Email：407541127@qq.com

褚衍杰（1982—），男，山东枣庄人，2005年于清华大学获学士学位，2008年于盲信号处理重点实验室获硕士学位，现为博士研究生，主要研究方向为信息处理。

CHU Yanjie Was born in Zaozhuang，Shandong Province，in 1982.He received the B.S.degree from Tsinghua UniversitY and the M.S.degree from KeY LaboratorY of Science and Tech_ nologY on Blind Signal Processing in 2005 and 2008，resPective_ lY.He is currentlY Working toWard the Ph.D.degree.His re_ search concerns information Processing.

User Association Mining Based on Spectral Clustering

WANG Yongcheng，CHU Yanjie
（National KeY LaboratorY of Science and TechnologY on Blind Signal Processing，Chengdu 610041，China）

For mining association relationshiP from user's geograPhical sPatial distribution data，a neW meth_ od based on sPectral clustering is ProPosed.FirstlY，the correlation degree is defined，Which is used to measure the similaritY of sPatial distribution of users，and then the similaritY matrix is constructed.Cluste_ ring analYsis is conducted bY using sPectral clustering method，and the relationshiP betWeen users is charac_ terized bY clustering results.The Silhouette index and clustering accuracY are used to measure the qualitY of user relationshiP mining，meanWhile the traditional K-Means method is comPared With the ProPosed algo_ rithm.ExPeriments on real data set shoW that the algorithm can achieve more than 90%of the clustering accuracY，indicating that the method is effective and feasible.

user behavior analYsis；user association mining；sPectral clustering；correlation degree；K-Means

TP393

A

1001-893X（2016）01-0032-06

10.3969/j.issn.1001-893x.2016.01.006

王永程，褚衍杰.基于谱聚类的用户关联关系挖掘[J].电讯技术，2016，56（1）：32-37.[WANG Yongcheng，CHU Yanjie.User associa_ tion mining based on sPectral clustering[J].Telecommunication Engineering，2016，56（1）：32-37.]

2015-10-22；

2015-12-29 Received date：2015-10-22；Revised date：2015-12-29

**通信作者：407541127@qq.com Corresponding author：407541127@qq.com