AA-CAES系统建模与储能阶段的热力特性
贾 祥,崔 凝
(华北电力大学 能源动力与机械工程学院,河北保定071003)
AA-CAES系统建模与储能阶段的热力特性
贾 祥,崔 凝
(华北电力大学 能源动力与机械工程学院,河北保定071003)
为了研究AA-CAES系统的热力特性,在500 kW-TICC系统的基础上设计了20 MW先进绝热压缩空气储能系统的热力模型,采用集中参数法建立了系统的动态数学模型,再以理论建模和数字仿真的方法研究了先进绝热压缩空气储能系统储能阶段动态特性。分析了压气机环节、换热器环节、储气罐环节和储热罐环节的动态特性,以及压气机进口流量变化导致系统各个设备参数变化的特性。仿真结果表明,第一级压气机比较稳定,二三级压气机波动较大,进气流量对各级换热器的出口冷工质和压气机的耗功影响较大,储气室内气体的温度变化比较平缓。
压缩空气储能系统;数学模型;仿真;动态特性
0 引言
电力储能系统是大规模利用可再生能源迫切需要,可以很好的改善甚至是弥补可再生能源的不稳定和间歇性,是智能电网和分布式能源系统的关键技术[1-3]。目前已在商业系统中大规模(如100 MW以上)运行的储能系统只有抽水电站和压缩空气两种[2-4]。压缩空气储能系统可适用于大型系统、并且工作时间长、储能周期不受限制、系统成本低、寿命长、安全性和可靠性高等优点。
德国1978年建成了世界上第一个商业性的CAES电厂——Huntorf电站,电站能量转化效率43%[5]。美国在Alabama州1991年建成了世界上第二个商业性的CAES电厂—McIntosh电站,此电站是在德国Huntorf电站基础上增加了回热器用来回收余热,使系统的热效率提高了25%[6]。美国Ohio州从2001年起开始建一座 2700 MW 的大型 CAES 商业电站,该电站由9台300 MW机组组成[7]。日本国内的新能源基金会和电力开发公司等单位从90年代开始,研究建造一座35 MW验电站,试验装置规模是未来商业化设备的1/10[8]。
另外国家电网公司牵头设立重大科技专项,由清华大学牵头,中国科学院理化技术研究、中国电力科学研究院所合作开展大规模压缩空气储能发电系统关键技术研究,已建成500 kW非补燃式压缩空气储能示范系统[9],文献[10]对此系统进行了详细介绍。年越对先进压缩空气储能系统热力性能进行了模拟研究[11]。韩中合刘士名等对AA-CAES电站进行了热经济性分析[12],很少有人研究AA-CAES系统的动态特性。本文以华北电力大学 STAR-90 仿真支撑系统为平台,在500 kW先进绝热压缩空气储能系统的基础上设计了20 MW先进绝热压缩空气储能系统,并且对系统储能阶段进行建模与仿真,对其热力特性和动态特性进行了研究。
1 系统介绍
AA-CAES系统称为先进绝热压缩空气储能系统,此系统主要设备有压气机、空气透平、换热器、储热器、泵、储气室、阀门;此系统的创新点有:(1)压缩热回收使得综合利用效率高;(2)低碳效益显著;(3)高能量密度;图1为系统图。
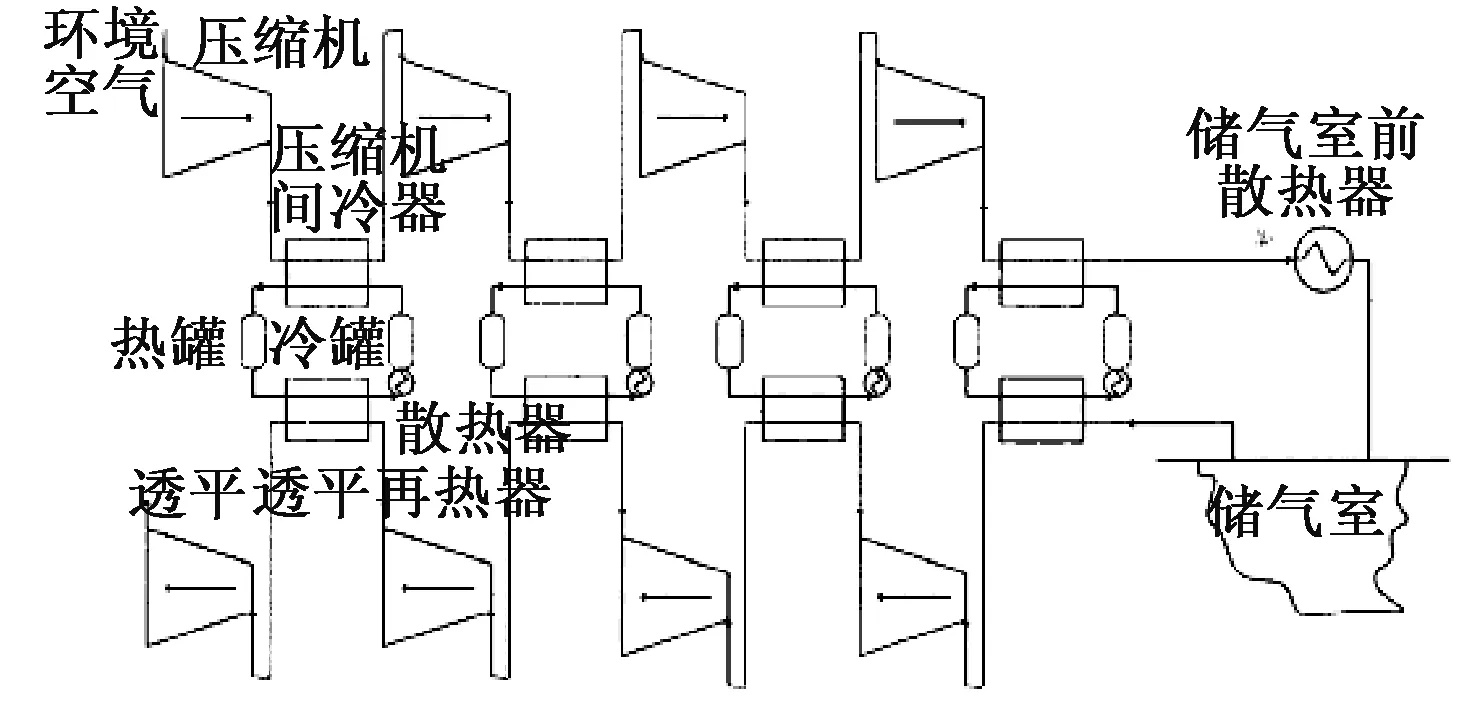
图1 AA-CAES系统
2 系统设计
2.1 压气机压比
(1)
(2)
式中:To,j为压气机出口空气温度,K;Ti,j为压气机入口空气温度,K;pi,j为上一级压气机入口空气压力,Pa;pi,j+1为下一级压气机入口空气压力,Pa;n为多变指数;Z为压气机级数;εt为压缩级总压比;ε1为每一级压气机压比。
压气机压缩的实际中不可避免的存在于外界换热,属于不可逆过程,因此压气机环节按多变过程处理[13],四级压气机实际总耗功:
(3)
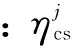
假设压缩过程中管道中没有压力损失,则上一级压气机出口空气压力等于下一级压气机入口空气压力[14],即有po,j=pi,j+1,对pi,2求偏导得:
(4)
(5)
结合式(4)与式(5)可得各级压比:
由等熵关系,各级排气温度均为139 ℃。为防止储气罐压力波动引起末级压缩机压比突升,使气缸温度过高,需要将末级压比取的较低[15],根据文献[16]有:
(6)
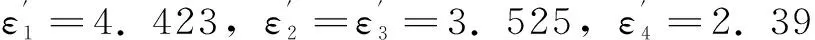
2.2 储气室参数
储气室采用定容储气室,以储气罐作为储气容器,系统输入功率为20 MW,设定充气时间为8 h,则理论上存储的能量为:
E=Pt
(7)
储气罐容积为:
(8)
式中:E为储气罐内存储的能量,kJ;P0为大气压力,Pa。
3 模块数学模型
3.1 压气机
质量平衡方程:
(9)
能量平衡方程
(10)
压气机流量方程:
(11)
压气机耗功功率方程:
(12)
式中:m1、m2为进出口压气机的流量,kg/s;在仿真计算中,认为进出口压气机的流量相等时为m,kg/s;Δp为某工况压强降,MPa;Δpr为设计工况压强降,MPa;mo为压气机额定流量,kg/s;ρ为压气机内空气密度,kg/m3;h1,h2分别为压气机进出口空气比焓,kJ/kg;Q为压气机内空气对外放热,kJ,η为压气机绝热效率。
3.2 换热器
空气侧能量平衡方程:
(13)
金属蓄热方程:
(14)
冷却工质出口温度:
(15)
式中:Ms为换热器内的工质质量,kg;ms为换热器内工质流量,kg/s;Cpw为换热器内水定压比热,kJ/(kg·K);Mw为换热器内水的质量,kg;Dw为换热器内水的流量,kg/s;Hs1,Hs2为工质入口、出口焓值,kJ;Q1为热流体释放的热量,kJ;Q2为冷流体吸收的热量,kJ;Mm为金属管子的质量,kg;Cm为金属管子的比热,kJ/(kg·K);Tm为金属管子温度,K;Ts1,Ts2为冷流体入口、出口温度,K;Tw1,Tw2为冷流体入口、出口温度,K。
传热方程:
(16)
(17)
式中:α1,α2为热冷流体换热系数。
采用隐式欧拉公式:
(18)
(19)

(20)
(21)
3.3 流体网络数学模型
流体的流动是一个连续的过程,各个设备的参数是相互联系的。各个设备或者系统压力,流量关系可以概括为一个流体网络模型。
根据质量守恒方程:
(22)
式中:M为压力节点P0内的流体质量,kg;G1,G2,G4为流入压力节点的流量,kg/s;G3为流出压力节点的流量,kg/s。
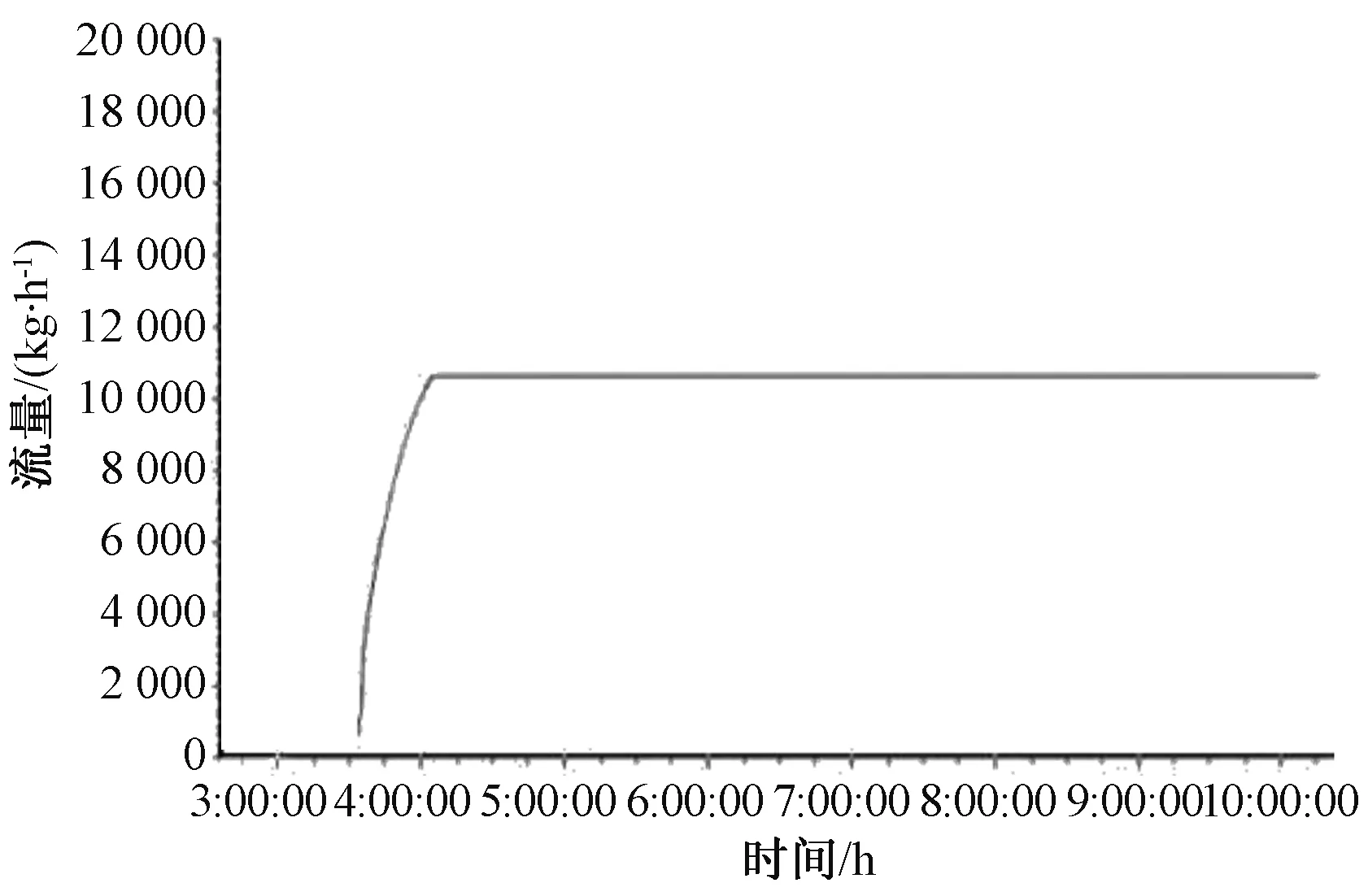
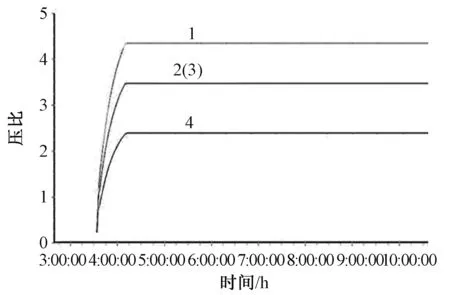
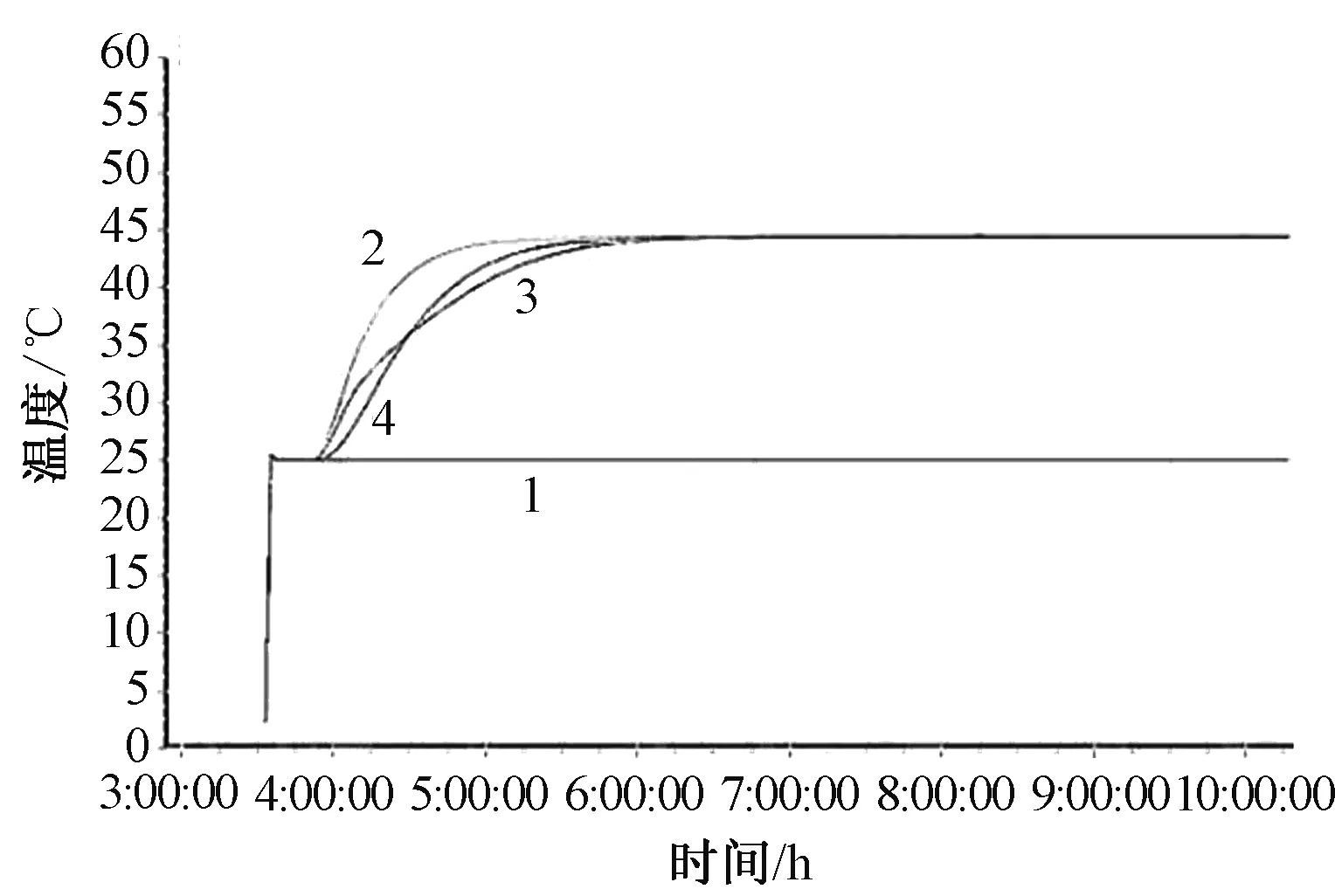
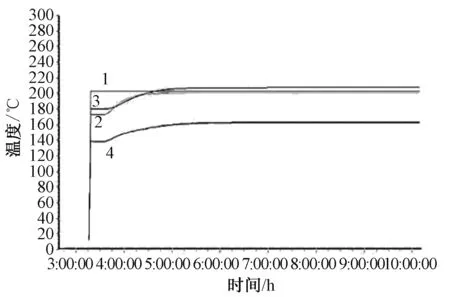
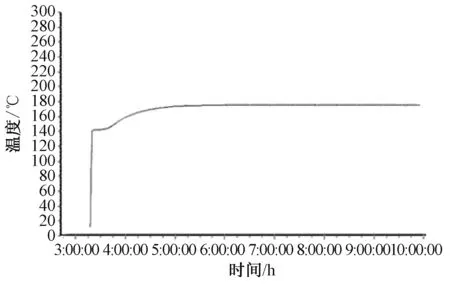
在图2所示的流体网络模型中,假设压力节点P1,P2,P3已知,假设P1,P2>P0,P3 (23) 式中:B1,B2,B3为线性导纳。 图2 流体网络节点 采用隐式欧拉公式转化为差分方程整理得: (24) 3.4 联箱数学模型 联箱在NF-CAES系统中,起到合流和分流的作用。在储能阶段,冷水罐内的冷水通过联箱分流,进入换热器降低压气机入口空气温度。在释能阶段,热水罐内的热水通过联箱分流,进入换热器提高透平机入口空气温度。 进入联箱的总流量满足: (25) 联箱内流体温总计算: (26) 联箱内流体焓总计算: (27) 联箱流体出口温度计算: (28) 联箱流体出口焓值计算: (29) 式中:G1in,G2in,G3in,G4in为联箱各个入口流体流量,kg/s;h1in,h2in,h3in,h4in,hout为联箱各路入口流体焓值及出口焓值,kJ/kg;T1in,T2in,T3in,T4in,Tout为联箱各路入口流体温度及出口温度,℃;Q为联箱与外界的热交换量,kJ;M为联箱内积存的流体质量,kg。 以华北电力大学 STAR-90 仿真支撑系统为平台,对系统储能阶段进行仿真,对其热力特性和动态特性进行了研究。每个图横坐标都是时间为6 h,纵坐标代表对应的变量,有的图中标有1、2、3、4分别代表第一、二、三、四级。通过仿真值和设计值相比较误差范围满足精度要求。 从图3可以看出,流量以很快的速度增大到压气机最大设计流量113 400 kg/h,流量达到平衡所需要的时间相对于整个系统的仿真时间很短,流量稳定时间为30 min。 图3 流量变化 由图4和图5可以看出,各级压气机压比以很快的速度增加到额定压比,第一级的增加速度最大,下来依次是二到四级,然后趋于稳定。由于各级压气机的压比逐渐增加到额定值,导致各级压气机的出口压力也随着压气机压比的变化上升到最大值,由图中可以看到三条线,那是因为第二级和第三级压气机的额定压比相等,两条趋势线重合,各级压气机出口压力的变化速度和压比相对应。 图4 压气机压比 图5 压气机出口压力 由图6中可以观察到第一级压气机的入口温度保持环境温度25 ℃不变,其它三级的入口空气温度逐渐增大到设计入口温度45 ℃,并且温度增大速度最快为第二级,第四级的增加速率刚开始大于第三级,后来被第三级赶上。 图6 压气机入口空气温度 由图7看出第一级压气机出口空气的温度不变,第二三四级的出口空气温度刚开始有一段时间也处于不变状态,随后处于上升状态再趋于平衡,最后第二三级出口空气温度基本一致,焓值是温度的函数,因此各级压气机出口空气焓值变化趋势和温度的一致。 图7 压气机出口空气温度 由图8看出四级压气机总耗功刚开始以相对快的速度增加,后来增加速度减慢最终达到平衡,总耗功达到平衡的时间为90 min。 图8 压气机总耗功功率 由图9可以看出刚开始各级换热器出口空气有一小段时间保持不变且相等,后来第四级保持不变的时间比较短,出口空气温度以最快的速度上升,经过一段时间后第三级出口空气温度以一定的速度上升,最终达到平衡,其中第二级和第三级的增加速度不稳定,刚开始第二级大于第三级,后来小于第三级。 图9 换热器出口空气温度 由图10可以看出各级压气机的出口空气温度有一小段时间保持不变,后来处于上升状态最后趋于平衡状态,其中第四级保持不变的时间段最短,并且温度上升的速率都大于一二三级的出口工质温度,下来依次是第一级、第三级的增加速度刚开始大于第四级,后来小于第四级。 图10 换热器冷工质出口温度 仿真过程中设定热罐环境压力为0.4 MPa,这样是为了使热罐的水温可以升的更高,由图11可以看出热罐水温刚开始变化缓慢,后来变化速度增大,最后以缓慢的速度达到平衡。 图11 热罐水温变化趋势 储气室压力(图12)逐渐由大气压力增加到储气室的额定压力,增加的速度接近线性函数。图13可以看出储气室气体温度由一开始到仿真结束都一直以缓慢的速度上升,这是由于往储气室内充气相当于压缩过程,会产生压缩热,因此会导致气体温度升高,温度变化速率越来越慢,最后阶段几乎接近不变。 图12 储气室气体压力 图13 储气室气体温度 (1)储能阶段第四级压气机压力增加速度最快;各级压气机的压比和出口压力受流量变化影响较大。 (2)储能阶段第一级压气机入口温度稳定性比后几级好,第二级的压气机入口温度变化最大;压气机出口空气温度第二三级变化速度最快。 (3)第三级换热器冷工质出口温度最大,并且随着各压气机出口温度增大而增大,入口空气流量对换热器出口水温也有很大的影响,综合起来影响各级换热器出口水温的因素有进口空气流量、压气机压比、各级换热器进气温度。 (4)压气机进气温度和流量同时影响系统耗功,当流量达到平衡以后,压气机耗功的变化相对平缓,流量变化对压气机耗功的影响大于压气机进口空气温度造成的影响。 (5)储气罐的压力变化接近线性变化,储气罐内气体温度变化平缓,储气罐气体焓值在高压状态下主要受气体压力的影响。 [1]JENSEN J. Energy storage[M]. London:Newnes-Butterworths,1980. [2]MCLARNON F R,CAIRNS E J. Energy storage[J]. Annual Review of Energy,1989,14(13):241-271. [3]CHEN H,CONG T N,YANG W,et al. Progress in electrical energy storage system:A critical review[J]. Progress in Natural Science,2009,19(3): 291-312. [4]RIBEIRO P F, JOHNSON B K, CROW M L,et al. Energy storage systems for advanced power applications [J].Proceedings of the IEEE,2001,89(12):1744-1756. [5]TER-GAZARIAN A. Energy storage for power systems[M]. London:Peter Peregrinus Ltd,1994. [6]张新敬,陈海生,刘金超,等.压缩空气储能技研究与进展[J].储能科学与技术,2012, 1(1):26-40. [7]SEPTIMUS V D L. The case for CAES [J].Modern Power Systems,2002,7(24):19-21. [8]GIRAMONTI A J,SADALA R L.Concept screening of coal gasification CAES systems[R]. Final Report ,1979:3-7. [9]陈来军,梅生伟,王俊杰,等. 面向智能电网的大规模压缩空气储能技术[J]. 电工电能新技术,2014, 33(6):1-6. [10]MEI S W,WANG J J,TIAN F,et al. Design and engineering implementation of non-supplementary fired compressed air energy storage system : TICC-500 [J]. Science China(Technological Sciences),2015,58(4):600-611. [11]年越.先进压缩空气储能系统热力性能模拟研究[D].北京:华北电力大学, 2015:16-19. [12]韩中合,刘士名,周权,等.蓄热式 AA-CAES 电站性能计算及经济性分析[J].华北电力大学学报(自然科学版),2015,42(5):87-93. [13]HARTMAN N, VOHRINGER O,KRUCK C,et al.Simulation and analysis of different adiabatic compressed air energy storage plant configurations[J].Applied Energy,2012,93(1):541-548. [14]张学林,王思贤,季伟,等. 500kW绝热CAES空压机优化设计[J]. 压缩机技术,2015 (1):16-19. [15]周佃民.压缩空气系统节能技术综述[J]. 上海节能,2010,10(8):36-41. [16]宋敏. 天然气压缩机组配置优化设计[J]. 天然气工业,2008,28(1):122-124. JIA Xiang, CUI Ning(College of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China) AA-CAES System Modeling and Thermal Properties of Energy Storage Phase In order to study the thermal characteristics of the advanced adiabatic compressed air energy storage system, an advanced model of 20 MW for the adiabatic compressed air energy storage system based on the 500 kW filling system of compressed air energy storage is designed. Using the lumped-parameter method to establish the dynamic mathematical model of the system, theoretical modelling and numerical simulation method to study the phase dynamic characteristics of the advanced adiabatic energy storage for the compressed air energy storage system, this paper analyzess the dynamic characteristics of the different links, such as the compressor, heat exchanger, storage tanks and heat storage tank, and the characteristics of the device parameters changing with the compressor inlet flow are also studied . The simulation results show that the first stage compressor is stable, while the compressors in second and third stages become volatile. The inlet flow rate for the export of all levels of the heat exchanger and cold working medium have a greater influence on the compressor power consumption; on the other hand, the indoor gas temperature changes more gently. compressed air energy storage system; mathematical model; the simulation; the dynamic characteristics 2016-07-05。 贾祥(1990-),男,硕士研究生,研究方向为先进绝热压缩空气储能系统热力特性研究,E-mail:934137684@qq.com。 TM73 A DOI:10.3969/j.issn.1672-0792.2016.09.012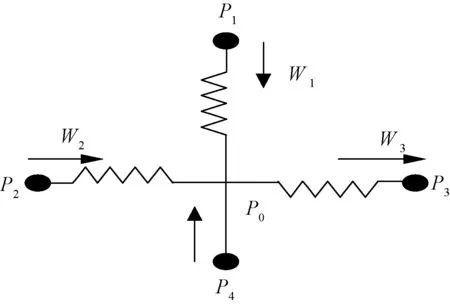
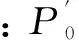
4 系统储能阶段仿真






5 结论

