改进形态滤波器在电力系统信号检测中的应用

王佳琦，盛四清

(华北电力大学 电气与电子工程学院，河北保定071003)



改进形态滤波器在电力系统信号检测中的应用

王佳琦，盛四清

(华北电力大学 电气与电子工程学院，河北保定071003)

由于传统广义自适应形态滤波器难以应对电力信号采集现场噪声复杂多变的情况，结合前人的研究提出了一种改进滤波方法，采用多组结构元素，并使用变步长的自适应算法集中加权，构建了一种新的多结构元素自适应形态滤波器。相比较传统的形态滤波器，改进滤波器用处更广，使用更加灵活。仿真结果表明，改进的形态滤波器能有效抑制电力采样信号中的复杂噪声，滤波效果优于传统广义自适应形态滤波器，使用更加灵活，并且当噪声发生变化时可以保证输出结果稳定，具有较强的适应能力。

数学形态学；自适应滤波；多结构元素；信号检测

0 引言

为确保电力系统稳定运行，需要对电力运行数据进行实时监测。但是电力数据的现场采集过程中，由于输配电环境的复杂，对信号产生干扰的因素非常多，采集到的信号包含了复杂多变的噪声，使测量的精度难以保证，不利于分析系统的运行状态。随着智能电网建设的深入，传感器、测量仪器、通讯设备的大量使用加剧了这一问题的严重性，而迅速准确地获取电力数据又是实现智能电网的重要环节。这考验了滤波器的消噪能力，现有的滤波器仍有不少改进的空间[1-4]。

数学形态学广泛应用于计算机视觉、模式识别和图像降噪等技术，近年来也被引入到电力系统数据的现场采样当中[5-7]。数学形态学仅在时域运算，不需要变换到频域，计算结果无相位移动与幅度衰减，具有简单快速的特点，很多性能均优于小波分析理论，因此得到越来越多的关注和应用。数学形态滤波主要通过合理的结构元素对待处理信号进行形态开-闭和闭-开运算，达到消噪的目的，其中结构元素的选取是影响滤波效果的关键因素[8，9]。

传统数学形态滤波器只根据某一特定的噪声，选择单一形状和尺寸的结构元素，难以达到滤波要求[10，11]。实际的电力信号中的噪声繁杂多变，当信号噪声种类变化时，通过选定的结构元素种类很难有效消除新的噪声。为了解决这一问题，本文结合多尺度全方位滤波的思想，构建了一种改进的基于多结构元素的自适应形态滤波器，并进行了仿真分析，通过与传统形态滤波器对比，证明了改进滤波器有更好的滤波效果，并能很好地适应噪声的变化。

1 数学形态学滤波原理

1.1 基本运算

数学形态学以积分几何和集合论为基础，其结构有易于并行实现的特点，处理速度具有天然优势。数学形态学的运算思想是利用一个人为设定的结构元素对目标信号进行“探测”，结构元素在信号中不断移动的同时收集信号各个部分的信息，直至提取信号全部的有用特征[12]。

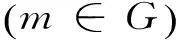
(1)

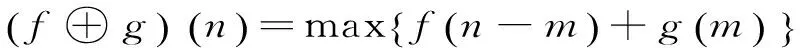
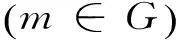
(2)

腐蚀和膨胀只涉及加减运算，计算简便，快速灵活。由腐蚀和膨胀进行不同的组合可以得到开运算和闭运算，公式分别为：

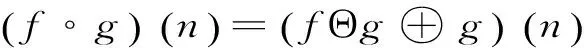
(3)

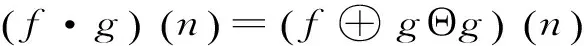
(4)

数学形态学滤波当中，结构元素作用就相当于滤波窗口，其形状和尺寸严重影响了滤波的效果。一般来说，结构元素越复杂，降噪效果越好，抗干扰能力越强，但是运算速度也越慢。

在一维数学形态学滤波中，结构元素有直角、三角、圆形、半圆、余弦、扁平、多次曲线、多边形及其组合等各种形状。大量的实验表明，处理不同的信号，需要选择匹配程度高的结构元素形状才能得到较好的效果。另外，结构元素的尺寸选择也很重要，尺寸太小会使滤波不完整，噪声会有残留；反之，若尺寸太大则可能会消除信号中的有用信息，造成信号失真，而且运算量加大，耗时过长。

1.2 广义形态滤波器

以此为基础，P.Maragos 用同一结构元素，构建了形态开-闭滤波器和形态闭-开滤波器[13,14]，其定义分别为：

(5)

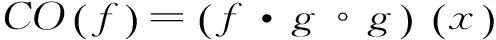
(6)

开-闭滤波器与闭-开滤波器二者单独使用时均易造成信号幅值的失真。为了提高滤波效果，尽量减少信号幅值的失真，通常使用二者的组合：

(7)

这种运算可以抑制信号中的正负脉冲噪声，但是形态开的收缩性和形态闭的扩展性，造成滤波信号存在偏倚现象，不利于实际应用。首先进行的运算会增加后级运算要消除的噪声，如果两次运算采用相同尺寸的结构元素，就不能有效滤除全部噪声。文献[13]选择不同尺寸的结构元素g1和g2，且g1≤g2，构成了一种广义开-闭和闭-开滤波器：

(8)

(9)

其中g1⊆g2。

1.3 自适应形态滤波器

(10)

(11)

则输出信号为：

(12)

输出信号与理想信号的均方差为

(13)

结合最小均值算法(LMS)，得出权系数的迭代公式如下：

(14)

其中μ为步长因子，可控制算法的收敛速度。原理如图1所示。

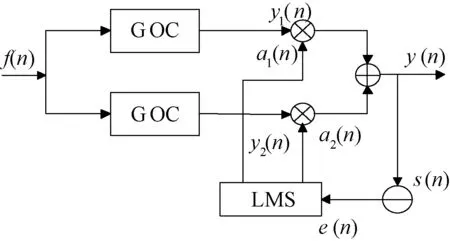
图1 传统自适应形态滤波器原理图

传统自适应广义形态滤波器只改变了两个结构元素的尺寸而采用相同的形状，然而信号经第一个结构元素进行开或闭运算后，几何特征会发生改变，必然导致同一形状的结构元素与信号匹配度下降，文献[16]尝试使用形状不同的结构元素g1和g2，优化滤波效果。

1.4 改进的形态滤波器

实际测量中，噪声有着多样的种类和尺度，成分复杂多变，难以选出一组结构元素应对各种噪声。尤其当信号噪声性质发生变化时，传统单组结构元素形态滤波器的滤波效果会有所下降。为了提高形态滤波器的抗干扰能力，本文从多尺度全方位滤波和模糊多变量控制算法的思想出发，尝试使用多组不同形状和尺度的结构元素对信号进行纵向并行处理，经过自适应算法进行加权组合，希望达到更好的去噪效果，以适应实际电力信号采集时噪声复杂多变的环境。

本文提出的多结构元素广义形态学滤波器原理如下：

(15)

用改进的多结构元素形态滤波器构造自适应形态滤波器，对于采用l组结构元素的滤波器，将2l个并行运算后的输出量进行自适应算法，确定每个输出的加权系数，然后得到最终输出结果为：

(16)

经由多组结构元素进行开-闭和闭-开运算后，得到的输出量滤波效果越好，采用自适应算法后，其在最终的输出结果中占有的比例越大。

使用自适应算法对步长因子μ很高的要求，合适的步长因子可以在算法达到很高精度的同时保证快速收敛。由于多结构元素形态滤波器的运算量较传统滤波器要大，所以要慎重选择合适的步长μ。

(17)

经由传统广义形态滤波器改进而成的多结构元素广义形态学滤波器，选择多种形状和尺度的结构元素进行组合，如g11，g12均为余弦结构元素，g21，g22均为半圆形结构元素；也可以令g11，g12形状不同，g11为余弦结构元素，而g12为三角结构元素，由于不同的噪声适合由不同的结构元素来处理，因此将可能取得较好滤波效果的各种形状和尺度的结构元素组合均考虑在内，组建成的多结构广义形态滤波器结构图如图2所示。

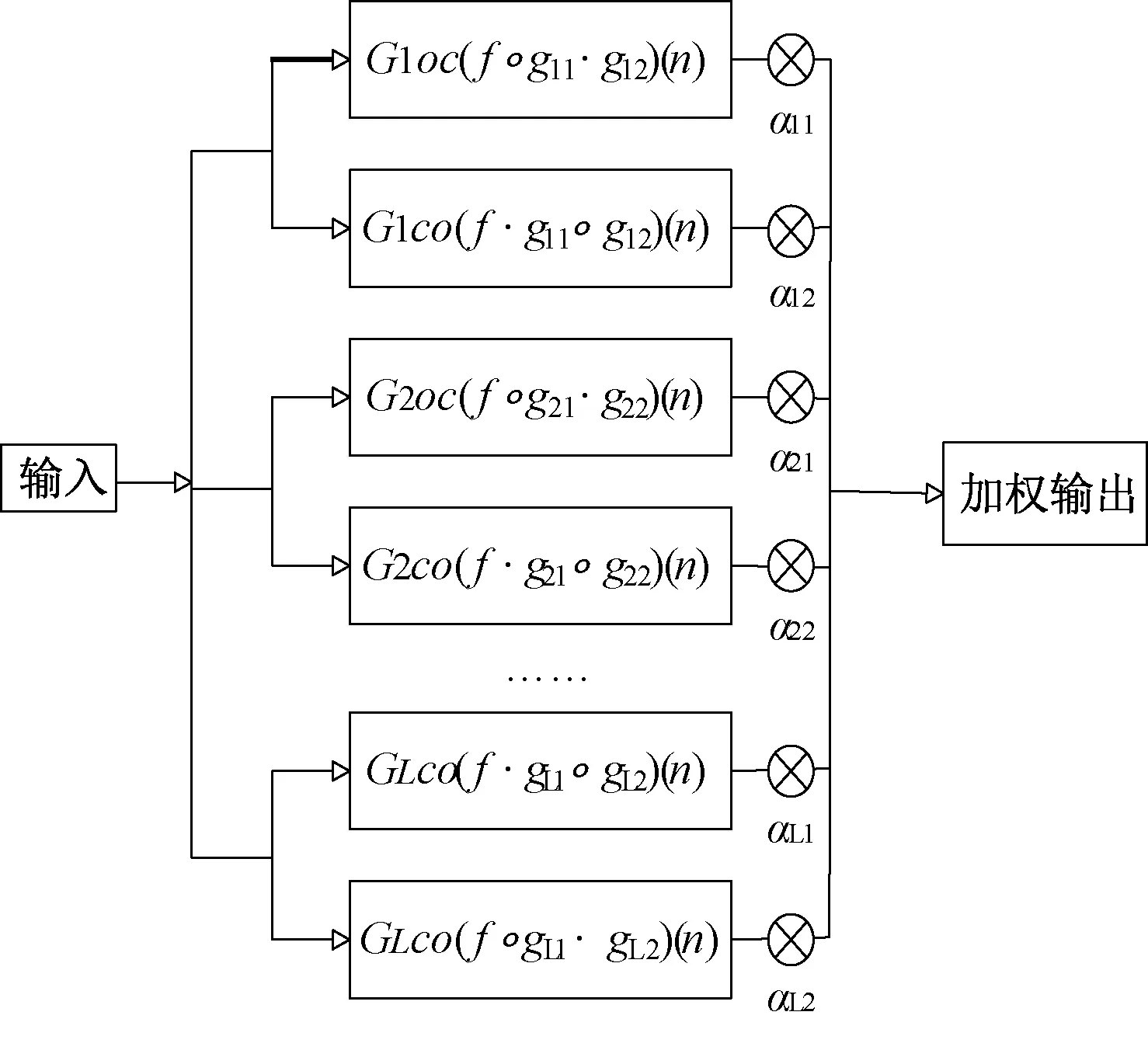
图2 改进多机构元素自适应形态滤波器

多结构元素的广义形态滤波器应用了多种形状和尺度的结构元素，特别适合处理采集到的噪声类型复杂多变的电力信号。设计时，尽可能采用滤波效果好的结构元素组合，相比较传统的形态滤波器，用处更广，使用更加灵活，适应环境变化能力更强。

2 仿真分析

2.1 概述

电力系统数据的现场采集中，较为常见的几种噪声为高频连续噪声、随机噪声和突发性脉冲噪声。本文在 50 Hz 的工频信号中混入这几种噪声作为原始含噪信号，然后通过改进的形态滤波器进行滤波分析，并与传统的形态滤波器进行比较。然后改变信号的噪声种类，检验改进滤波器对变化环境的适应能力。

数据对比时，采用信噪比(QSNR)和均方根误差(ERMSE)作为评价标准对滤波效果进行衡量，计算公式为：

(18)

(19)

2.2 初始噪声仿真结果分析

待处理信号的基波为幅值取1 V，频率取50 Hz的正弦信号，在此基础上先叠加了三种噪声：(1)10 kHz连续高频噪声，幅值为0.1 V；(2)均值为0，功率为0.01的随机白噪声；(3)幅值为0.8的突发性脉冲噪声。

首先使用传统自适应滤波器进行仿真，在满足g1⊆g2的条件下，选择不同形状、长度和幅值的结构元素进行处理，经过大量实验记录，比较信噪比(SNR)和均方根误差(RMSE)，选出三组滤波效果最优的结构元素，其尺寸、形状、幅值和滤波效果记入表1。图3和图4给出了原始含噪信号与分别采用以上三种结构元素的传统滤波器处理后的信号。

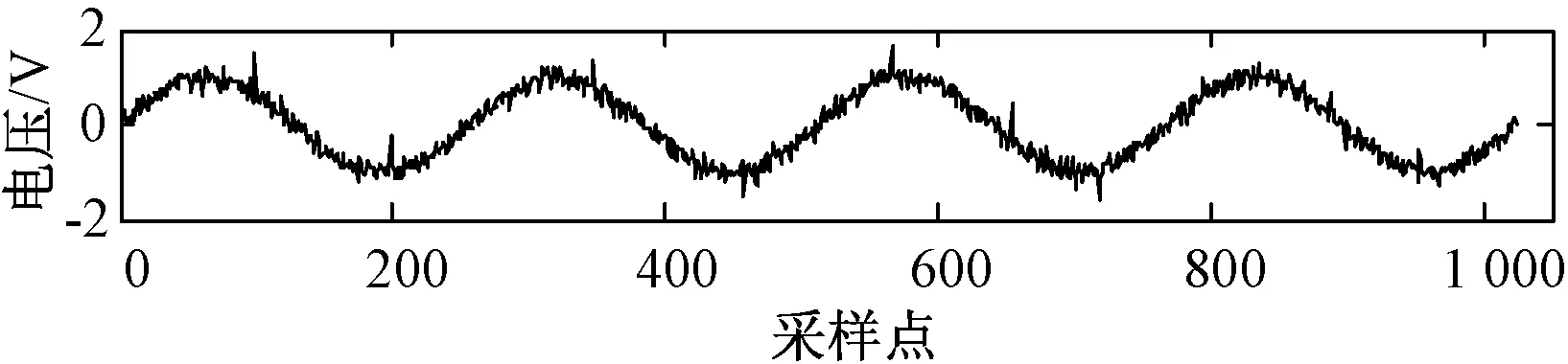
图3 初始含噪信号

改进的自适应形态滤波器使用这三组结构元素的组合：滤波器一使用两组结构元素(g11，g12)和(g21，g22)；滤波器二使用(g21，g22)和(g31，g32)；滤波器三使用(g11，g12)和(g31，g32)；滤波器四中使用这三组结构元素。改进滤波器自适应算法的步长初值μ0=0.1，根据调试，当选取α=2，β=1时，算法收敛速度和精度达到最优。在与之前相同的噪声条件下，仿真得出四种改进的多结构元素形态滤波器滤波效果如图5和表2所示。

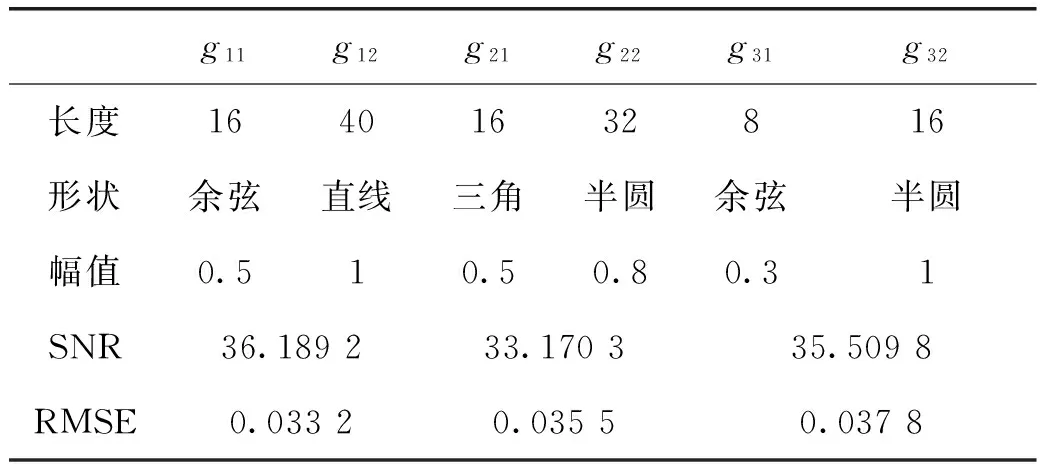
表1 三组传统形态滤波器处理结果

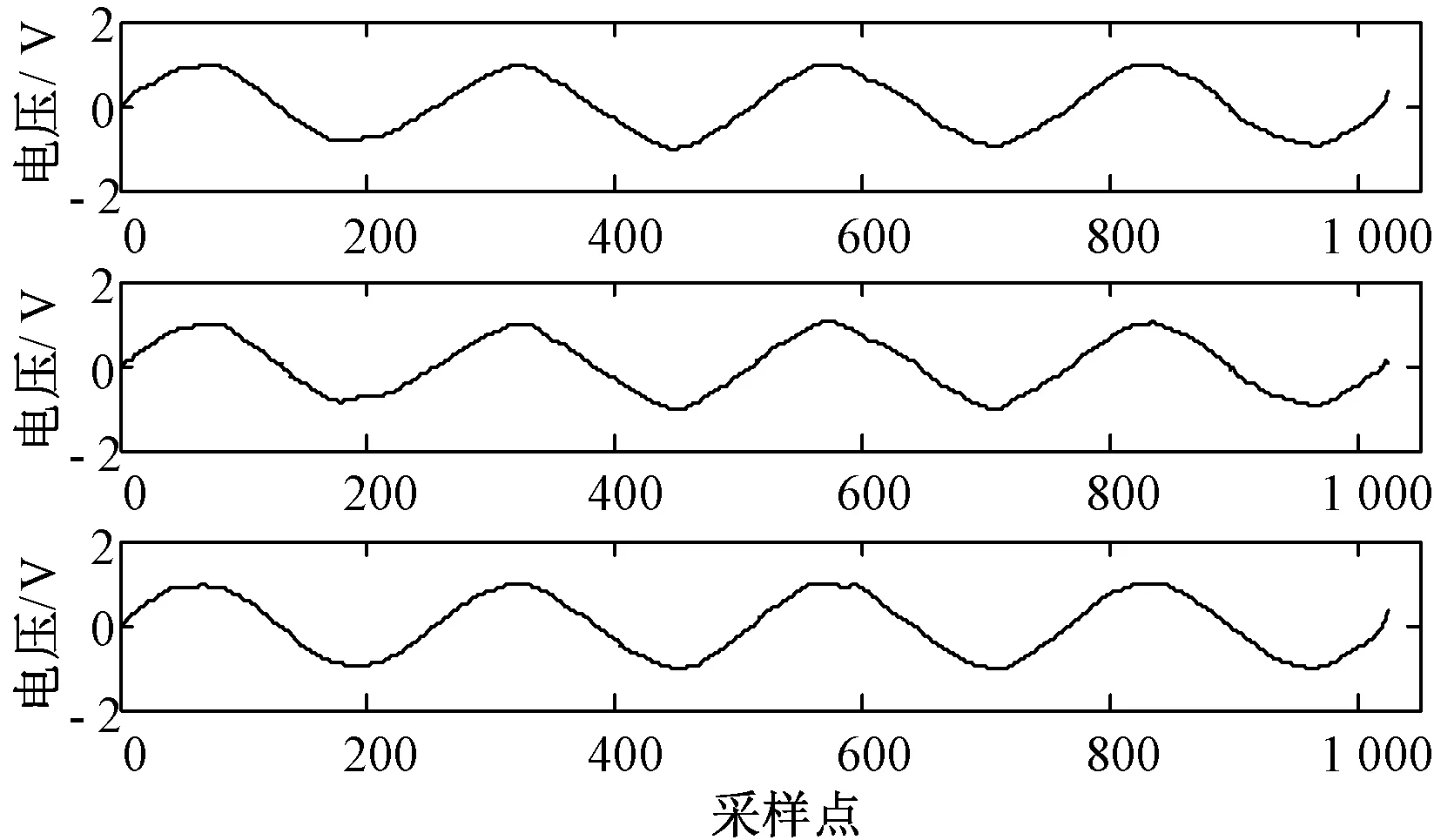
图4 三组传统形态滤波器处理结果

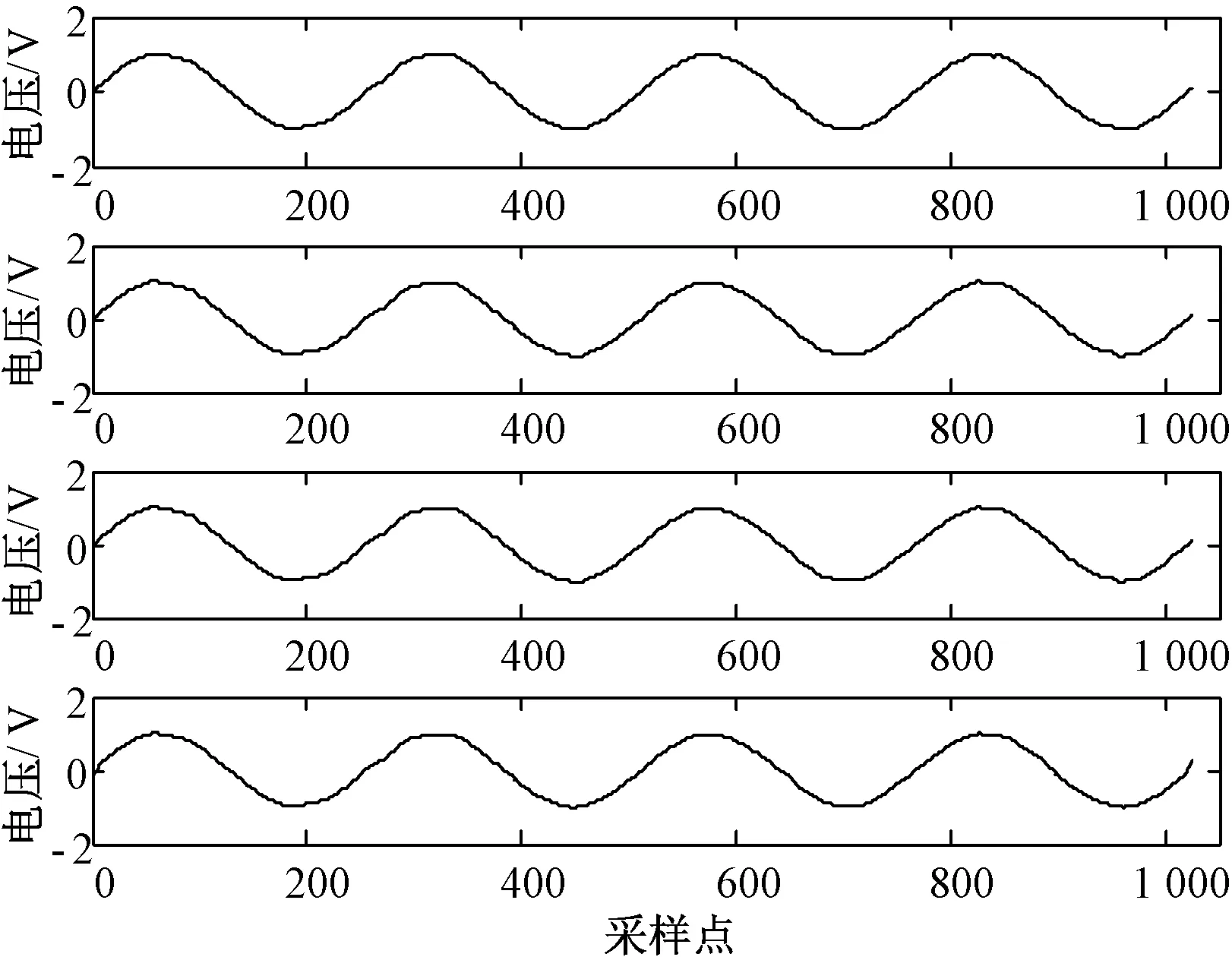
图5 改进多结构元素形态滤波器处理结果

表2和图4的仿真结果表明，对比信噪比和均方根误差，多结构元素自适应形态滤波器的效果均优于传统单组结构元素形态滤波器；采用三组结构元素的改进滤波器4的效果优于前三种采用两组结构元素的改进滤波器。结果表明，在改进的自适应滤波器中，并入的良好的结构元素越多，滤波效果越理想。

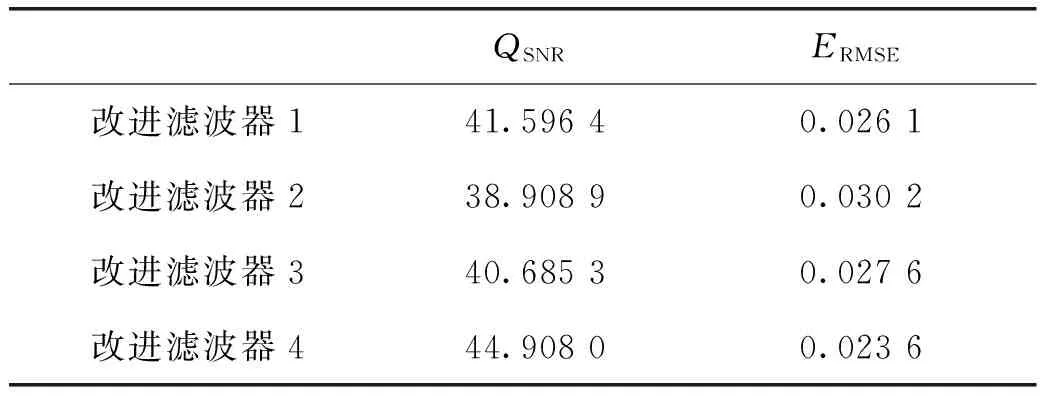
表2 改进多结构元素形态滤波器处理结果

2.3 噪声变化时仿真结果分析

现场采集时，电力信号包含的噪声性质有时会有一定程度地变化，对滤波器的滤波能力提出了考验。本文通过改变信号的噪声种类，检验改进滤波器对变化环境的适应能力。

基波不变，对所加的三种噪声进行适当改变：(1)10 kHz连续高频噪声，幅值为0.2 V；(2)均值为0，功率为0.03的随机白噪声；(3)幅值为1的突发性脉冲噪声。图6为噪声改变后的信号波形。然后分别使用第一次选出的三种传统形态滤波器和改进的滤波器对信号进行处理，仿真结果分别为图7，图8。将得到的信噪比与均方根误差记入表3进行对比。

图6 改变后的含噪信号

表3 噪声改变后滤波效果对比

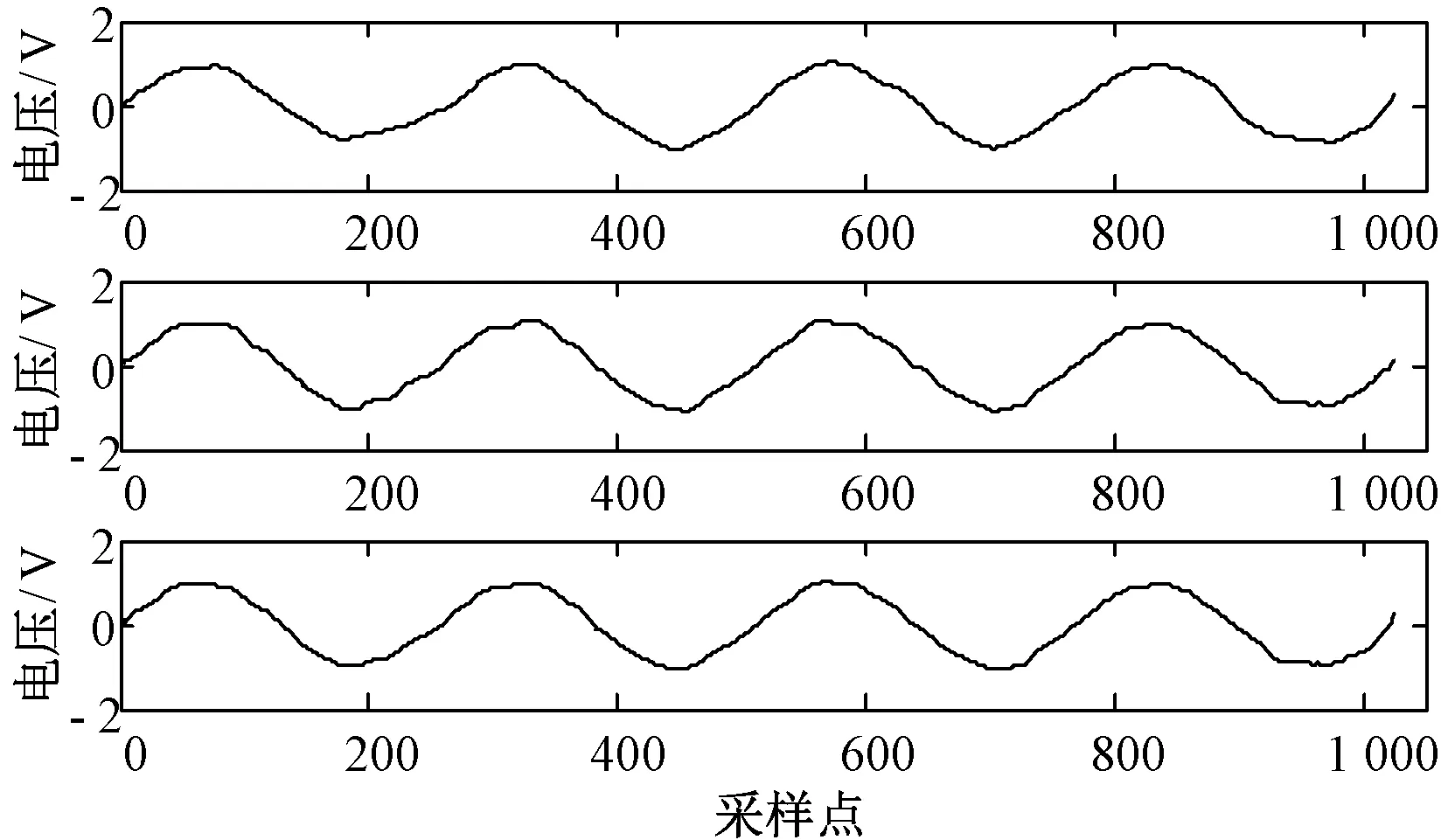
图7 噪声改变后传统滤波器处理结果

图8 噪声改变后改进滤波器处理结果

可以看出，当信号噪声发生变化时，传统滤波器滤波效果下降较明显，说明实际电力信号中所含噪声改变时，使用传统滤波器会使误差增大，而采用改进的滤波器性能下降幅度较传统滤波器小，滤波结果可以接受。

2.4 第二次改进滤波器仿真结果

为了验证多结构元素思想，针对改变后的噪声，选择出一组滤波效果较好的结构元素(g41，g42)，将其依次与第一组改进滤波器结合，组成新的改进滤波器，其在两种噪声下的滤波结果如图9、10和表4所示。

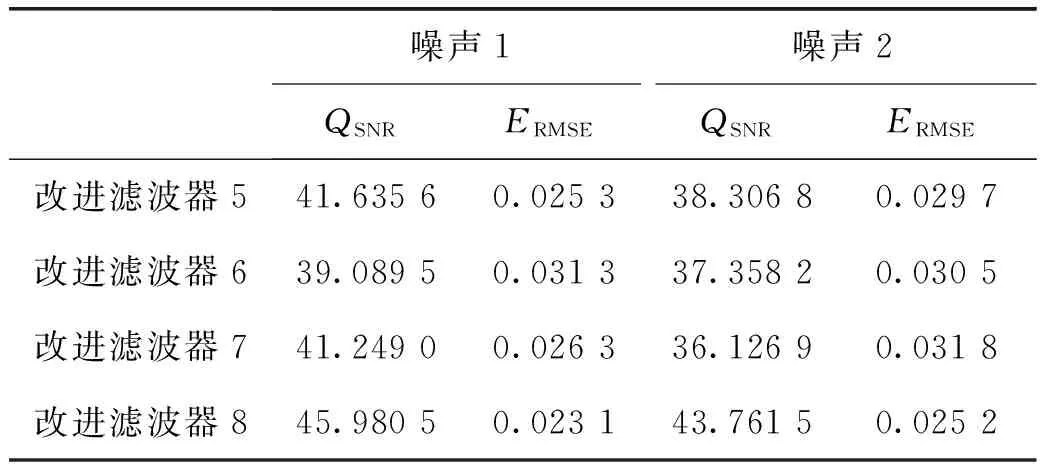
表4 两种噪声下的滤波效果

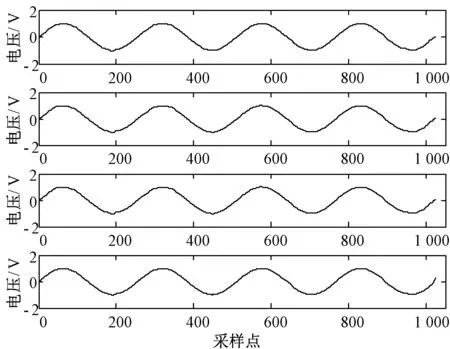
图9 新的改进滤波器对第一种噪声处理结果

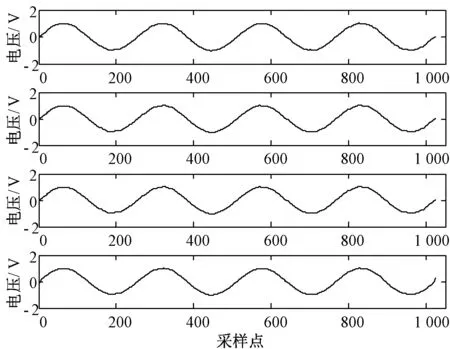
图10 新的改进滤波器对第二种噪声处理结果

结果表明，并入(g41，g42)后改进滤波器在第一种噪声下的滤波效果变化不大，但在第二种噪声下滤波效果有了明显改进，进一步验证了采用多结构元素并行的思想是有效的。

经过以上分析可以看出，多结构元素自适应形态滤波器的效果比传统滤波器要好，而且随着并入的结构元素增多而变得更好。当信号噪声属性改变时，改进滤波器比传统滤波器受影响更小，输出结果更加稳定，即采用多结构元素的形态滤波器具有更强的适应能力。不足之处在于，使用的结构元素组数较多时计算量会相应增加，对滤波的速度造成影响。因此可以根据实际情况，在保证精度的情况下，选择合适组数的结构元素，确保计算速度。另外，还可以从自适应算法方面改进，选择更合适的补偿因子，或是寻找更有效的自适应算法。

3 结论

本文对传统的广义自适应形态滤波器进行了改进，通过使用多组结构元素并行开-闭和闭-开运算然后集中自适应加权，以适应噪声复杂变化的电力信号采样环境。仿真结果证明了改进滤波器精度更高，对噪声变化的环境适应性更强，且使用更加灵活。但是，由于计算量的增加，时效性可能会有所下降；同时实验中使用的测试信号仅能代表最为常见的情况，特定场合下使用改进的滤波器还需要根实际情况进行参数的调整，要应用到工程中还需进一步优化。

[1]刘盼,王静,刘涤尘.改进的自适应广义形态滤波器设计[J]. 电网技术,2009(2):94-98.

[2]王明俊. 智能电网热点问题探讨[J]. 电网技术,2009(18):9-16.

[3]谭向宇,许学勤,孙福,等. 新型自适应广义形态滤波在MOA在线监测数据处理中的应用[J]. 中国电机工程学报,2008,28(19):25-29.

[4]冯庆东,何战勇. 国内外智能用电发展分析比较[J]. 电测与仪表,2012,49(2):1-6.

[5]崔红芬,李鹏,王畅. 基于数学形态学的微网电压补偿量检测方法[J]. 中国电机工程学报,2013,33(16):122-128，10.

[6]郝文广,丁常富,梁娜. 小波降噪与FFT降噪比较[J]. 电力科学与工程,2011,27(3):59-61.

[7]王续东,曲延滨. 基于多级广义自适应形态学滤波的电力信号消噪[J]. 电测与仪表,2014(11):45-49.

[8]康军胜,刘桂英,廖耀华,等. 基于数学形态学滤波的电压暂降检测方法[J]. 电力科学与工程,2016,32(1):58-63.

[9]蒋章,邓艾东,蔡宾宏. 基于梯度法的自适应广义形态滤波在碰摩声发射信号降噪中的应用[J]. 中国电机工程学报,2011,31(8):87-92.

[10]赵昭,刘利林,张承学,等. 形态学滤波器结构元素选取原则研究与分析[J]. 电力系统保护与控制,2009,37(14):21-25，35.

[11]张筱辰,高宏力,黄海凤,等. 基于量子遗传算法的数学形态滤波器优化设计[J]. 西南交通大学学报,2014,49(3):462-469.

[12]沈路,周晓军,张文斌,等. 广义数学形态滤波器的旋转机械振动信号降噪[J]. 振动与冲击,2009,28(9):70-73.

[13]MARAGOS P，SCHAFER R W. Morphological filters-part I：their set theoretic analysis and relation to linear shift invariant filters[J].IEEE Transactions on ASSP，1987，35(8)：1153-1169.

[14]MARAGOS P，SCHAFER R W. Morphological filters-part II：their relation to median，order-statistic，and stack filters[J].IEEE Transactions on ASSP，1987，35(8)：1170-1184

[15]赵春晖，孙圣和.一种形态开、闭自适应加权组合滤波器[J].电子学报，1997，25(6)：109-111.

[16]卢锦玲,石少通,徐超,等. 含大型风电场系统暂态电压稳定性分析[J]. 华北电力大学学报(自然科学版),2014,41(1):45-52.

[17]张红梅,韩万刚.一种新的变步长LMS自适应滤波算法研究及其应用[J]. 仪器仪表学报,2015,36(8):1822-1830.

WANG Jiaqi, SHENG Siqing(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

Application of an Improved Generalized Adaptive Morphological Filter in Signal Detection of Power System

In view of the fact that the conventional adaptive generalized morphological filter is difficult to cope with the complex and changeable noises during power signal collection process, on the basis of the previous studies, an improved filtering method, using multi-structural elements and variable step size from centralized adaptive algorithm weights，is created to build a new multi-structural elements adaptive morphological filter. Compared to the traditional morphological filters, improved filters can be used more broadly, and is more flexible at the same time. Simulation results show that the improved morphological filter can effectively suppress the complex noise of the sampled power signal, and the filtering effect is better than traditional adaptive generalized morphological one, and can be used more flexibly. The improved morphological filter has a better adaptive ability, and when the noise changes the results could remain stable.

mathematical morphology; adaptive filter; multi-structural elements; signal detection

2016-06-13。

王佳琦 (1992-)，男，硕士研究生，研究方向为电力系统分析与控制、电能质量分析,E-mail： 15194701@qq.com。

TM932

A DOI:10.3969/j.issn.1672-0792.2016.09.002