架空输电导线机械起舞受力与频率关系的理论计算
谢文丽,王茂成,王冠宇,李 新,陈海亮,张志红
(1. 鲁东大学 物理与光电工程学院,山东烟台264025;2. 国网山东省电力公司 烟台供电公司,山东烟台264000;3. 山东省济南艾西特数控机械有限公司,山东济南250117)
架空输电导线机械起舞受力与频率关系的理论计算
谢文丽1,王茂成2,王冠宇2,李 新3,陈海亮1,张志红1
(1. 鲁东大学 物理与光电工程学院,山东烟台264025;2. 国网山东省电力公司 烟台供电公司,山东烟台264000;3. 山东省济南艾西特数控机械有限公司,山东济南250117)
导线舞动严重威胁输电线路正常工作,为了更深入研究架空输电导线舞动运动规律,根据输电导线舞动时导线做椭圆运动特点,计算得到利用机械数控设备模拟输电导线舞动时需要的力与频率和振幅的关系,绘制出架空输电导线舞动时所需外力与频率变化关系的曲线图,计算了档距100 m的单导线和双分裂导线在舞动频率从0.1 Hz变化到1 Hz范围时所受的外力大小。计算结果为利用人工机械的方法使架空输电导线产生椭圆轨道舞动提供理论依据。机械数控设备模拟输电导线舞动可以测量输电导线舞动时耐张串的扭转情况。由于条件所限,尚未完成耐张串扭转角的测量工作。
舞动;单导线;双分裂导线;椭圆轨迹;理论计算;
0 引言
输电导线舞动是在覆冰、风激励和线路结构参数因素影响下产生的低频(约为0.1~3 Hz)、大振幅(约为导线直径的5~300倍)的自激振动[1-7]。近几年,由于大范围低温、雨雪和冰冻等恶劣天气出现,河南、湖南、湖北、江西、山东等地输电线路相继出现大面积舞动情况。舞动导致多条线路发生闪络跳闸、绝缘子碰撞破损、跳线断裂、间隔棒等金具损坏断裂、杆塔结构受损、倒塔等事故[8-10],电网受到严重的破坏,影响用电安全[11,12]。国内外对输电导线的舞动从舞动机理、防舞措施[13-16]、模型与现场试验、数值模拟和计算机仿真等多方面进行了研究[6,17-22]。由于输电导线舞动的特点和各方面因素制约(如建设实验线路经费较大),目前导线舞动理论及舞动实验研究工作开展不够[9]。在舞动轨迹研究方面,根据邓哈垂直托舞动理论,一般舞动的轨迹总是椭圆形[1]。输电导线的舞动形成是一个逐渐趋于稳定的过程,导线上质点运动的轨迹为:由初始在平衡位置做微小的振动,到最后在风能和空气阻力的作用下,水平振幅慢慢变小,竖直振幅慢慢变大,然后形成不断变大的椭圆运动,最终受到平衡力的作用而趋于稳定。王有元[23]等利用集成加速度传感器,获取导线舞动时在垂直方向和水平方向的加速度,结合边界条件,求出垂直方向和水平方向的位移,并最终叠加成总位移的方式描述出导线舞动轨迹,给予了舞动的轨迹总是椭圆形实验方面的支持。张超[24]等分析了导线舞动时的运动特性,推导了基于惯性测量单元还原导线舞动轨迹的计算步骤,仿真结果验证了基于惯性测量单元还原导线舞动轨迹的可行性。还原出与真实情况相符的竖直和水平方向位移幅值。
位于河南省尖山的国家电网公司输电线路舞动防治技术研究是我国首座针对覆冰舞动研究建立的真型输电线路综合试验基地,围绕输电导线的舞动展开了广泛的研究[25-27],但利用机械舞动方面,目前没有见诸文献报道。为探讨导线舞动规律、实现精确控制机械舞动的可行性,从利用人工控制导线机械舞动,使输电导线舞动时导线做椭圆运动,分析计算得到导线舞动时受力情况以及与频率的关系,绘制出导线舞动时力与频率变化关系的曲线图,为利用机械方法使输电导线产生精确椭圆轨道舞动提供理论依据。本文首先介绍架空输电导线机械起舞受力与频率关系的计算方法,给出计算实例,绘制出导线舞动时力与频率变化关系的曲线图,最后给出结论。
1 实验模型与数学模型
1.1 实验模型
导线机械舞动实验模型[28]如图1所示。一般档距100 m以内只发生一阶舞动,故取实验档距100 m,机械舞动设备设在两侧终端钢管杆的中间位置,在机械舞动设备和左侧终端钢管杆的中间位置再设直线钢管杆,直线钢管杆上可挂悬垂串或V形串,两侧终端钢管杆挂耐张串、复合绝缘子耐张串、悬垂串或V型串与多分裂导线相连,左侧终端钢管杆上设有舞动监测装置,通过机械舞动装置和舞动监测装置的组合,调整机械舞动装置的舞动频率和导线弧垂,可实现对不同气象条件下导线和金具舞动、轨迹的监测,利用机械舞动中机械摇臂的作用力使得导线在竖直方向上做椭圆轨道运动,监测装置进行实时观测、记录复合绝缘子耐张串、悬垂串V形串在舞动过程中的运动轨迹。

图1 导线机械起舞模型示意图
1.2 数学模型
设输电导线机械舞动时轨迹是椭球面,建立oxyz直角坐标系,如图2所示,椭球方程为
(1)
导线舞动时导线上的各点的轨迹是椭圆(实线椭圆),如图3所示。以输电导线中心点M为研究对象,设M点运动的参数方程为

(2)
式中:ω是导线舞动时的圆频率;t是时间;a、b、c指的是导线舞动时在x、y、z轴方向上的最大振幅。

图2 输电导线舞动示意图
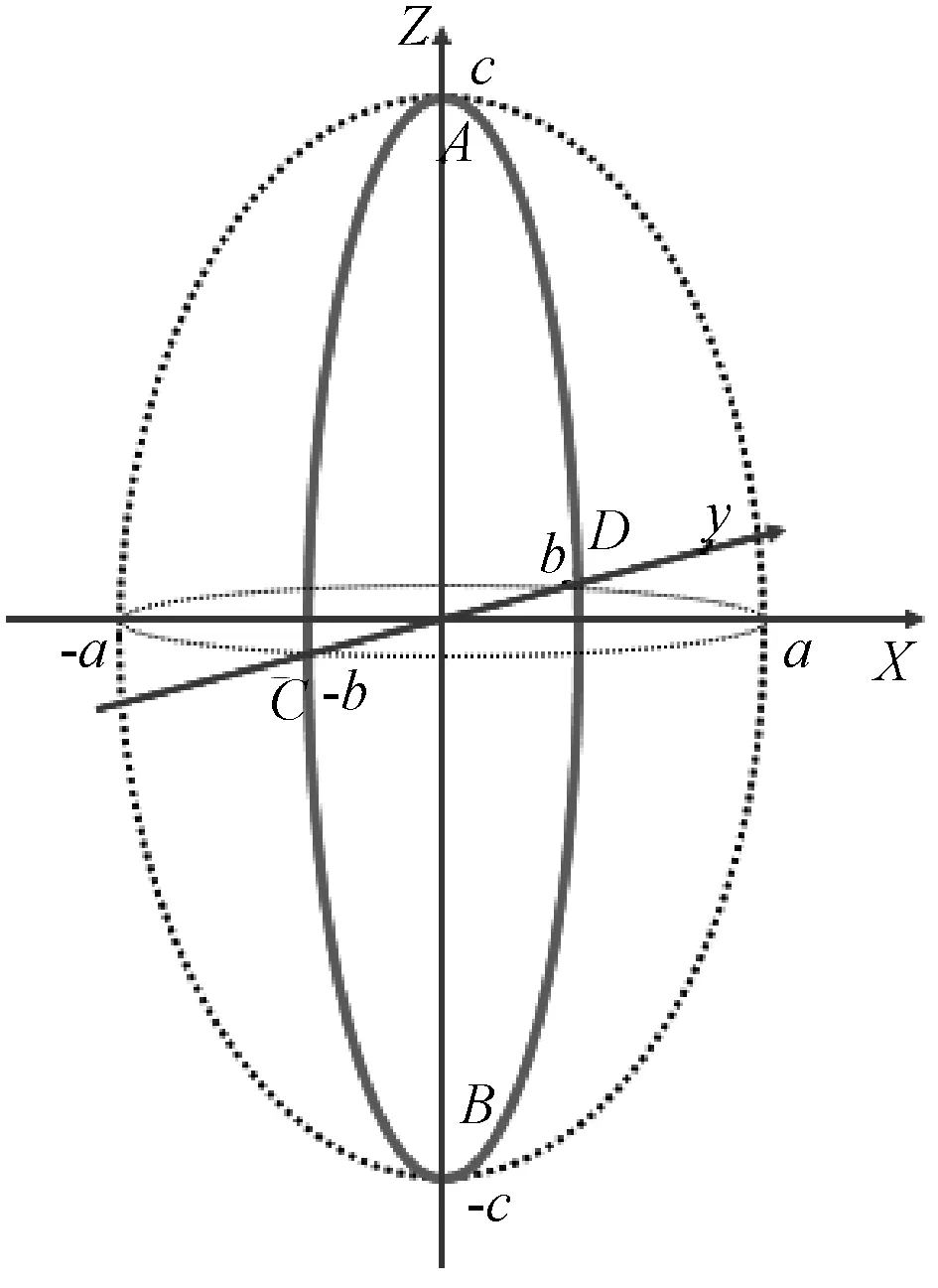
图3 输电导线中心点M运动轨迹

(3)

1.3 受力分析

(4)
式中:L是档距长度;θ角取值说明见图5。机械摇臂作用力NA在z方向的力为NAz,所以,沿z轴,输电导线中心点M受到的合力为:
得到
(5)
输电导线中心点M位于A点时受到的合力方向沿z轴,由重力、张力和机械摇臂作用力三者决定。在A点机械摇臂给与的支持力大小为:
(6)


图4 中心点M位于A点时受力分析

图5 中心点M位于A、B点时θ角关系图

图6 中心点M位于C、D点时θ 角关系图
1.4 计算实例
1.4.1假定条件
(1)钢管杆设计挠度为5‰,形变量为3 cm,钢管杆弯曲造成的影响可以忽略,以下计算均不考虑钢管杆的弯曲。
(2)近似认为输电导线舞动时弧垂不变。
(3)舞动幅度不大,输电导线舞动时材料形变较小,所以忽略输电导线弹性形变造成的影响,认为舞动时输电导线长度不变。
(4)因输电导线长度随温度变化较小,所以忽略输电导线长度随温度的变化的影响,作用在导线上的荷载均指向同一方向,且沿导线均匀分布。
(5)以档距为100 m为例(导线安全系数取2.5),则弧垂对输电导线长度的影响计算如下:
输电导线的自重力比载
式中:Q是每公里输电导线的质量,Q=1 307.5 kg/km;A是输电导线截面积,A=425.24 mm2;计算得g=3.015×10-2N/m·mm2。应力
式中:σ是输电导线最低点的最大允许应力;Tp是输电导线的拉断力,N;σ大小为额定抗拉强度(或计算拉断强度)的95%,2.5是输电导线安全系数,计算得到σ=94.45 N/mm2,根据两边等高的悬挂点间架空线的长度计算公式:
因实验档距比较小,计算时取前两项就可以达到实验要求的精度,计算得LAB=100.004 25 m,即弧垂对输电导线舞动时的长度影响只有0.004 25 m,可以认为弧垂对输电导线舞动时的长度影响较小,所以以下的计算忽略了弧垂对输电导线舞动时长度的影响。
1.4.2 计算参数
(1)档距取L=100 m,耐张串长度为2.445 m,档内实际输电导线长度为95.12 m。
100 m单导线 JL/LB20A-400/35型输电导线的质量取值:
1 307.5 kg/km×95.12 m=124.37 kg;每个耐张串质量:金具串27.1 kg;2支复合绝缘子25 kg,两端合计104.2kg;舞动时摇臂作用于输电导线中心点M的质量近似认为是输电导线质量和耐张串质量之和:m=104.2+124.37=228.57 kg。质量近似会使得力的计算结果偏大。
(2)档距100 m导线计算时安全系数取2.5。
(3) 单导线最大静态设计张力
舞动时最大张力取最大静态设计张力的2倍(河南电科院尖山真型舞动试验基地测试数据为1.6~1.7倍,计算中考虑实验安全因素,取2倍),所以单导线最大设计张力变化范围为:(40.166~80.332 kN)。
(4)档距100 m双分裂导线2×JL/LB20A-400/35舞动时重力负载取值:耐张串167.8 kg,单根导线质量为1 307.5 kg/km×95.12 m=124.37 kg,双分裂导线和耐张串的总质量为416.54 kg,耐张串和导线总重量为4 082.092 N。
(5)根据河南电科院尖山真型舞动实验数据,导线舞动频率大多在0.3 Hz左右,个别在0.6 Hz左右,档距100 m时频率取值范围为f=0.1~1Hz。
2 结果与讨论
2.1 双分裂导线受力分析
如图7所示, oxyz坐标系是固定坐标系ox轴水平向右,与输电导线走向一致,oz轴竖直向上,oy轴与ox轴、oz轴构成右手螺旋。

图7 直角坐标系的建立

图8 右导线受力分析

图9 左导线受力分析

图10 间隔棒受力分析
依据图8~10受力分析得到输电导线和间隔棒受到的重力与输电导线的张力满足
左导线:2Tsinθ=N间-导+G左导
(7)
右导线:2Tsinθ=N间-导+G右导
(8)
间隔棒2N导-间=G间
(9)
G左导=G右导
(10)
(7)+(8)4Tsinθ=G间+2G左导
单根导线静态张力取单导线的2倍80 332N,两根导线加耐张串重力4 082.092N,间隔棒重力取250N,计算得到sinθ=0.0135。当sinθ≈tanθ时,得到档距100m双分裂导线弧垂0.674 09m,与真实值接近,说明张力取值是合理的。计算取双分裂导线舞动时两根导线以及相间间隔棒舞动是同步的,双分裂导线机械舞动模型与单导线一样。
2.2 单导线力与舞动频率关系计算关系计算
根据以上计算公式和计算条件,得到100m单导线机械做椭圆轨迹舞动时,根据式(6)得到中心点在A点受到机械摇臂施加力的大小
式中:张力T分别取40.166kN和80.332kN;频率f取值0.1Hz到1Hz,得到NA随频率变化关系曲线,同样的方法得到中心点在B、C和D点时机械摇臂施加的力随频率变化曲线,如图11所示。NC和ND与y轴正方向的角度随频率变化曲线如图12所示。

图11 M点舞动至A、C、B、D点时N~f关系曲线

图12 NC和ND与y轴正向的角度变化的曲线
对于1×JL/LB20A-400/35型单导线,在实验档距100m、导线安全系数为2.5和导线舞动频率区间0.1~1Hz前提下,导线沿椭圆形舞动轨迹舞动时由图11(a)得到导线中心点在最高点时机械摇臂作用力在频率为0.1Hz到0.7Hz附近NA先沿z轴正向逐渐减小,后沿z轴反向增加,也就是频率相对较低时机械摇臂的作用力为沿z轴的支持力,当频率变大时机械摇臂的作用力变为沿z轴负向的拉力;力的方向总是沿z轴方向。椭圆形舞动轨迹中心点在最低点B时由图11(c)得到机械摇臂作用力在导线张力为40.166kN时机械摇臂的作用力随频率沿z轴正向逐渐增大,而在导线张力为80.332kN时机械摇臂的作用力随频率先沿z轴负向减小,后沿z轴正向增大,力的方向总是沿z轴方向;而当中心点在与档内中央点在同一水平面上的C点时,由图11(b)得到张力在40.166kN时,机械摇臂的作用力在频率为0.1Hz到0.4Hz附近时逐渐减小,由图12(a)得到力的方向与y轴正向所呈角度逐渐增大,直至垂直,在0.4Hz附近到1Hz时机械摇臂的作用力逐渐增大,力的方向与y轴正向所呈角度又逐渐减小,而在张力T为80.332kN时,机械摇臂的作用力0.1Hz到0.6Hz时逐渐减小,力的方向与y轴正向所呈角度逐渐增大,直至垂直,机械摇臂的作用力在0.6Hz到1Hz时又逐渐增大,力的方向与y轴正向所呈角度又逐渐减小;而当中心点在与档内中央点在同一水平面上的D点时,因C点和D点导线受力一样,所以机械摇臂的作用力的变化情况和C点一样。
2.3 双分裂导线力与舞动频率关系计算
根据以上计算条件和分析,得到100 m双分裂导线机械做椭圆轨迹舞动时,利用公式(6)得到中心点在A点受到机械摇臂施加力的大小
式中:张力T分别取80.332 kN和160.664 kN;频率f取值0.1 Hz到1 Hz,得到NA随频率变化关系曲线。同样的方法得到中心点在B、C和D点时机械摇臂施加的力随频率变化曲线,如图13所示。

图13 M舞动至A、C、B、D点时N~f关系曲线
对于2×JL/LB20A-400/35型双分裂导线,在实验档距100 m、导线安全系数为2.5和导线舞动频率区间0.1~1 Hz前提下,导线沿椭圆形舞动轨迹舞动时由图13得到导线中心点在机械摇臂的作用力下,舞动频率在0.1~1 Hz之间时,机械摇臂在A、C、B和D点对导线中心点的作用力随频率变化趋势与档距100 m单导线是一样的,只是力的大小不一样。
由于单导线的扭转刚度为线性的,而分裂导线的扭转刚度为非线性的,且分裂导线的扭转刚度远远大于单导线的扭转刚度,从而导致分裂导线更易发生舞动,分裂导线的扭转刚度设计的因素比较复杂,目前的大部分计算都是建立在单导线的基础之上[29-32]。机械数控设备模拟输电导线舞动可以测量输电导线舞动时耐张串的扭转情况,即在一个內弧U型环上采用小抱箍固定弹簧针,在另一个內弧U型环上采用小抱箍固定画板,耐张串转动过程中,弹簧针在画板上涂鸦,即可得到轴向转动角。由于条件所限,尚未完成耐张串扭转角的测量工作。
3 结论
综合以上分析得到,机械摇臂施加的作用力的值最大在单导线中心点舞动至最低点B点,舞动频率为1 Hz导线张力为40.166 kN时,其值是9.647 kN;最小也是在导线中心点舞动至最低点B点,舞动频率为1 Hz导线张力为40.166 kN时,其值是0.723 kN。分裂导线比单导线更易发生舞动,机械摇臂施加的作用力的值最大在双导线中心点舞动至最低点B点,舞动频率为1 Hz导线张力为80.332 kN时,其值是17.296 kN;最小也是在导线中心点舞动至最低点B点,舞动频率为0.1 Hz导线张力为1.033 kN时。计算结果可为后续机械舞动实验提供参考。计算过程中将质量集中到导线中心点的假设会导致计算的机械摇臂作用力偏大。实验安全可靠。本文工作中仅考虑竖直和水平方向二自由度的驰振情况的椭圆轨迹运动规律,没有考虑输电导线扭转舞动对椭圆轨道的影响[1]。
[1] 郭应龙,李国兴,尤传永.输电线路舞动[M].北京:中国电力出版社,2003.
[2] WANG J, LILIEN J L.Overhead electrical transmission line galloping[J] . IEEE Transactions on Power Delivery, 1998,13(3): 909-916.
[3] SHUHART J H.Vibration damper for transmission lines: U.S, US2694101[P] .1954-.
[4] DESAI Y M, SHAH Y A H, POPPLEWELL N. Perturbation-based finite element analyses of transmission line galloping[J]. Journal of Sound and Vibration, 1996, 191(4): 469-489.
[5] LI X, ZHU K, LIU B. Research of experimental simulation on aerodynamic character for typed iced conductor[J]. Aasri Procedia, 2012(2):106-111.
[6] GARCIASANCHEZ D, ZANDE A M V D, PAULO A S, et al. Imaging mechanical vibrations in suspended graphene sheets[J]. Nano Letters, 2008, 8(5):1399-1403.
[7] NIGOL O, CLARKE G J. Conductor galloping and control based on torsional mechanism[C]//IEEE Transactions on Power Apparatus & Systems,1981,PAS-100(2):708-720.
[8] 刘连睿.我国高压架空线路导线舞动情况及分析[J]. 华北电力技术,1989(9): 40-43.
[9] 黄经亚. 500kV 输电线路中山口大跨越 5 次导线舞动的分析及探讨[J]. 电力技术, 1990(4): 14-20.
[10] 张予. 架空输电线路导线覆冰在线监测系统[J]. 高电压技术, 2008, 34(9): 1992-1995.
[11] RAWLINS C B. Research on vibration of overhead ground wires[J]. IEEE Transactions on Power Delivery, 1988, 3(2): 769-775.
[12]GUPTA S, WIPF T J, FANOUS F, et al. Structural failure analysis of 345 kV transmission line[J]. IEEE Transactions on Power Delivery, 1994, 9(2): 894-903.
[13] 范钦珊,官飞. 覆冰导线舞动的机理分析及动态模拟[J]. 清华大学学报( 自然科学版), 1995,35(2): 34-40.
[14] 蔡延湘. 输电线舞动新机理研究[J]. 中国电力,1998,31(10): 62-66.
[15] DAVIS D A,RICHARDS D J W,SCRIVEN R A. Investigation of conductor oscillation on the 275 kV crossing over the rivers severn and wye[J].Proceedings of the Institution of Electrical Engineers, 1963, 110(1): 205-219.
[16] 尤传永,卢明良.架空输电线路导线舞动的防止措施[J] .中国电力, 1993( 8): 41-43.
[17] 朱宽军,刘彬,刘超群,等. 特高压输电线路防舞动研究[J] .高电压技术,2007,33(11): 61-65.
[18] 朱宽军,尤传永, 赵渊如. 输电线路舞动的研究与治理[J] .电力建设, 2004, 25(12): 18-21.
[19] 卢文生,陈亦. 大跨越输电线体系风荷载模拟[J]. 特种结构, 2004, 21(3): 12-14.
[20] 朱宽军,刘超群,任西春. 架空输电线路舞动时导线动态张力分析[J] .中国电力, 2005, 38(10): 40-44.
[21] 雷川丽,段炜佳,侯镭,等. 架空输电线舞动的计算机仿真[J] .高电压技术, 2007, 33(10): 178-182.
[22] 张帆,熊兰,刘钰. 基于加速度传感器的输电线舞动监测系统[J] .电测与仪表, 2009, 46(1): 30-33.
[23] 王有元,任欢,杜林. 输电线路导线舞动轨迹监测分析[J] .高电压技术, 2010,36 (5): 1113-1118.
[24] 张超,吴旺林,杜永峰, 等. 输电线舞动轨迹还原理论与试验研究[J] .低温建筑技术, 2015, 37(7): 58-60.
[25] 卢明,葛亚峰,魏建林,等. 真型试验线路次档距振荡的观测与分析[J] . 电力建设, 2015,36( 11): 123-129.
[26] 杨晓辉,楼文娟,陈贵宝,等. 导线舞动对输电杆塔作用的试验技术[J] .振动、测试与诊断,2015,35(5):973-976.
[27] 邵颖彪,杨晓辉,郭薇,等. 基于九轴传感器监测导线舞动的研究方法[J]. 智能电网, 2015, 5(1): 1-8.
[28] 王云波,王茂成,张志红,等.一种复合绝缘子金具串舞动实验装置:CN 105136192 A[P] .2015.
[29] 傅观君, 王黎明, 关志成,等. 架空输电线路分裂导线扭转刚度及舞动机理分析[J]. 高电压技术, 2013, 39(5):1273-1280.
[30] 蔡文彪. 500 kV输电线路覆冰舞动跳闸原因与对策[J]. 东北电力技术, 2009, 30(12):35-37.
[31] 魏冲, 潘少成, 唐明贵,等. 500kV输电线路舞动分析及治理[J]. 电力建设, 2011, 32(4):22-25.
[32] 张天光, 孙东海, 敖清诚,等. 河南电网500kV姚邵线舞动事故分析与治理措施[J]. 电力建设, 2009, 30(3):24-27.
XIE Wenli1, WANG Maocheng2, WANG Guanyu2, LI Xin3, CHEN Hailiang1, Zhang Zhihong1*(1. Ludong University, Physics and Optoelectronic Engineering College, Yantai 264025, China;2. Yantai Electric Power Supply Company of Shandong, Yantai 264000, China;3. Shandong Ecth Nc Machine Co., Ltd., Jinan 250117, China)
Theoretical Calculation on Relationship Between Force and Frequency of Overhead Transmission Conductor Mechanical Galloping
The transmission line galloping can be a severe threat to the normal work of transmission lines. In order to study the movement regularity of the overhead transmission conductor galloping deeply,we have analyzed the relationship between the values of the outside force,frequency, and amplitude by using mechanical numerical control equipment analog the transmission galloping. The curves of the force for a single conductor and bundle conductor, changing with the frequency whose range covers from 0.1 Hz to 1 Hz with the line span 100 m, are given in this paper. Theoretical calculation results provide a theoretical basis for the application of artificial mechanical to reproduce the elliptical galloping of the overhead conductors. The mechanical Computerized Numerical Control (CNC) equipment mocking transmission conductor galloping could be used to measure a series of torsion resistance.Due to the limitation of conditions, we have not yet completed measurements of the tension string of torsion angle.
wire galloping; singleconductor; twin bundled lines; ellipse tracking; theoretical calculation
2016-06-06。
国网山东省电力公司科技项目(2014A-23)。
谢文丽(1987-),女,硕士研究生,研究方向为原子与分子物理,E-mail:601217753@qq.com。
TM715
A DOI:10.3969/j.issn.1672-0792.2016.09.008

