基于支持向量机的储能逆变器电压控制策略研究

李继森, 林永君, 刘立立, 刘卫亮

(华北电力大学 控制与计算机工程学院，河北保定071003)



基于支持向量机的储能逆变器电压控制策略研究

李继森, 林永君, 刘立立, 刘卫亮

(华北电力大学 控制与计算机工程学院，河北保定071003)

微网孤岛运行中，由于储能逆变器带非线性负载时电流波动大，以及逆变器内阻不可忽略，导致输出端口电压波形难以控制。针对此问题提出了基于支持向量机(SVM)的复合逆控制策略。在分析支持向量机的基础上，采用了粒子群算法优化各参数。根据影响逆变器输出电压的相关扰动量，构建逆变器的逆模型结构，利用储能逆变器在不同工况下的运行数据训练支持向量机逆模型。将逆模型输出的占空比作为储能逆变器的输入，同时利用输出电压反馈，构成闭环控制，以提高系统的控制性能。仿真结果表明，该控制策略相比直接逆控制和双环PID控制能提高储能逆变器的动态性能并减少电压谐波含量。

储能逆变器；支持向量机；逆模型；谐波

0 引言

在微网系统中，储能逆变器作为能量转换器件必不可少，交直流变换过程中必须保证在带任何负载情况下输出电压波形的正弦度和准确性，其控制性能的优良直接关系到微电网的正常运行。由于逆变器输出侧LC滤波器的存在，逆变器输出阻抗不为零，所产生的输出电压降低。尤其是带非线性负载时，不连续的脉冲电流产生的瞬态压降将会造成输出电压波形的严重畸变。针对这个问题，许多学者专家提出了电压平均值控制策略、双闭环PID、无差拍控制、反复补偿及扰动观察反复补偿等控制方式，但是都有自己的局限性。双闭环控制具有较快的动态响应特性，但是控制器参数不易整定。无差拍控制在理论上具有控制偏差小的优点，但是对模型的依赖性较高。反复补偿技术能有效地抑制周期性波动负载的影响，但是选择控制增益比较困难[1-4]。

随着人工智能技术的不断发展，智能学习算法在对象辨识方面体现出了强大的生命力，比如神经网络、支持向量机等方法以其强大的逼近非线性映射的能力，大量的应用于辨识那些具有不确定性或高度非线性的被控对象。

本文提出利用复合逆模型控制技术，来解决逆变器带整流性负载电压难控制的问题。首先采用支持向量机的方法，建立逆变器的逆模型，根据逆变器的各种状态下运行数据对模型进行训练。逆模型配合PI闭环控制，得到良好的控制效果。另外，逆模型的控制结构简单、鲁棒性强、抗干扰能力也得到一定改善。

1 支持向量机的基本理论及优化

1.1 回归支持向量机原理

支持向量机(SVM)是由Vapnik于1995年提出的一种基于“小样本”的学习算法，目前可以将其分为支持分类算法(SVC)和支持向量回归算法(SVR)，前者主要用于辨识分类，后者主要用于函数逼近[5]。本文采用支持向量回归算法来逼近期望的占空比信号。

对于非线性支持向量机，用非线性回归函数表示为：

(1)

用来估计训练的样本集为D={(xi,yi)}，其中，i=1,2,…,n，xi∈Rd，yi∈R。

引入松弛变量ξi≥0，ξi*≥0，则训练集D中所有的n个样本(xi,yi)都应满足一下约束条件：

(2)

优化目标为

(3)

式中：C为用来平衡模型复杂项和训练误差的惩罚参数；ε为不敏感损失参数。

凸二次规划问题可以转化为以下对偶二次规划问题求解：

(4)

(5)

其中K(xi,xj)为核函数，一般为高斯核函数

求解上式便可求得非线性SVR的回归函数为：

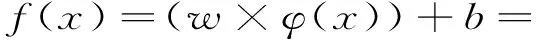
(6)

1.2 粒子群优化SVM模型参数

支持向量机模型建立的准确程度与惩罚参数C、不敏感损失函数ε以及核函数有很大的关系。参数选择的正确与否直接关系到支持向量机模型的准确性和泛化能力。本文中提出了利用粒子群算法(PSO)优化支持向量机的关键参数：惩罚参数C、不敏感损失参数ε以及核参数γ。

粒子群算法是由Kennedy和Eberthart于1995年受人工生命研究结果启发，在模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的进化计算技术[6-10]。PSO算法首先生成初始种群，也就是在可行解的空间中随机初始化一群粒子，每个粒子都为优化问题的可行解，并由目标函数为之确定一个适应值。每一个粒子在解的空间中运动，其运动的方向与距离受一个速度决定，通常粒子总是追随当前的最优粒子变化，经过逐代的搜索最后得到一个最优解[11]。

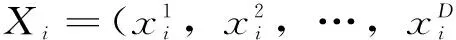
粒子群算法采用如下公式对粒子所在位置不断更新：

(7)

(8)

式中：i=1,2,…,m ；d=1,2,…,D；ω是非负数，称为惯性因子；加速常数c1和c2是非负数；r1和r2是[0，1]范围内变化的随机数；α称为约束因子，目的是控制速度的权重。

本文利用粒子群算法优化惩罚参数C，不敏感损失函数ε以及核参数γ，因此可以设置三维的目标搜索空间，每个群体规模可以设置为30个。根据支持向量机的特点，既要考虑到模型的准确性又要确保模型具有一定的泛化能力。另外在实际应用当中惩罚参数C要尽量小一些，这样计算复杂度会降低很多。在此设定粒子群的适应度函数为

(9)

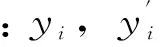
优化算法步骤为：

Step1：数据集的处理，确定支持向量回归模型的训练集和测试集。

Step2：粒子群初始化，设置粒子群体规模、初始位置及速度。

Step3：根据设置好的参数，进行模型训练，按照式(9)计算当前粒子适应度。保存当前个体最优和群体最优值。

Step4：按照式(7)、(8)更新粒子的速度及位置。

Step5：是否满足终止条件，若满足则终止运算，并确定最优的粒子及支持向量机模型的最佳参数；否则转至step3。

2 储能逆变器逆模型及控制策略

2.1 储能逆变器影响电压因素分析

微网中储能逆变器带整流性负载的拓扑结构如图1所示，udc为逆变器输入电压；r为考虑各种因素后线路等效电阻；电感L1和电容C2构成LC滤波器，整流负载上带阻感性负载L2和R，功率开关器件V1～V4构成逆变桥，采用双极性PWM脉宽调制方式，占空比为d，当开关频率足够高时，依据平均状态模型，有d=ui/udc。

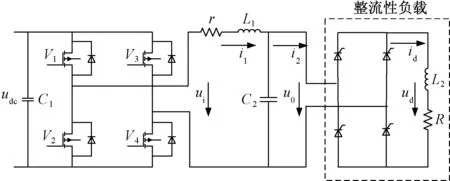
图1 储能逆变器拓扑结构

依据储能逆变器的拓扑结构，分析影响输出的变量如下:

(1)负载。负载的变化直接影响了系统的特性，从而影响了系统输出波形，这也是影响电压波形最主要的因素。但是负载的变化不能直接测量，只能通过检测输出电流，间接的反映负载切换，LC滤波器的电感电流呈现微分特性，具有一定的超前性，可以作为扰动量引入到电压控制当中。

(2)储能电池的输出电压udc。其值受储能单元工作状态影响，随着放电时间的增长，端口电压会出现较大波动，进而影响输出电压的稳态值。

(3)PWM控制信号占空比d。作为逆变器控制的输入量，直接影响逆变器的输出。

2.2 逆模型的建立

逆变器系统的输入输出的映射关系是非线性一一对应的，可以利用支持向量机学习算法建立逆变器的逆模型，即通过输出量来反推输入量。

(10)

这样就可以构造逆模型如图2所示。

图2 逆变器逆模型结构

2.3 输出反馈PID+逆模型复合控制

若将SVM辨识的逆模型的输出直接作为逆变器的输入，也就是将逆模型与逆变器串联起来，这样便使得期望的电压输出与逆变的输出之间的传递函数为1，构成伪线性系统。但是这是一种开环控制，控制起来比较简单，但是必须依赖于逆模型高精度，而在实际的运行当中，逆模型不可避免的存在一定的建模误差，再加上外界不可控的干扰，直接逆模型控制的控制动态性能和鲁棒性并不好。因此可以引入输出量反馈构成闭环系统，改善系统特性。

针对以上不足，本文提出闭环控制的思想，将逆变器输出电压进行反馈，与期望值求差值后进行PID运算，使输出紧随输入。增加闭环回路后，构成了复合控制器，系统的动态性能和鲁棒性得到了显著提升，控制框图如3所示。

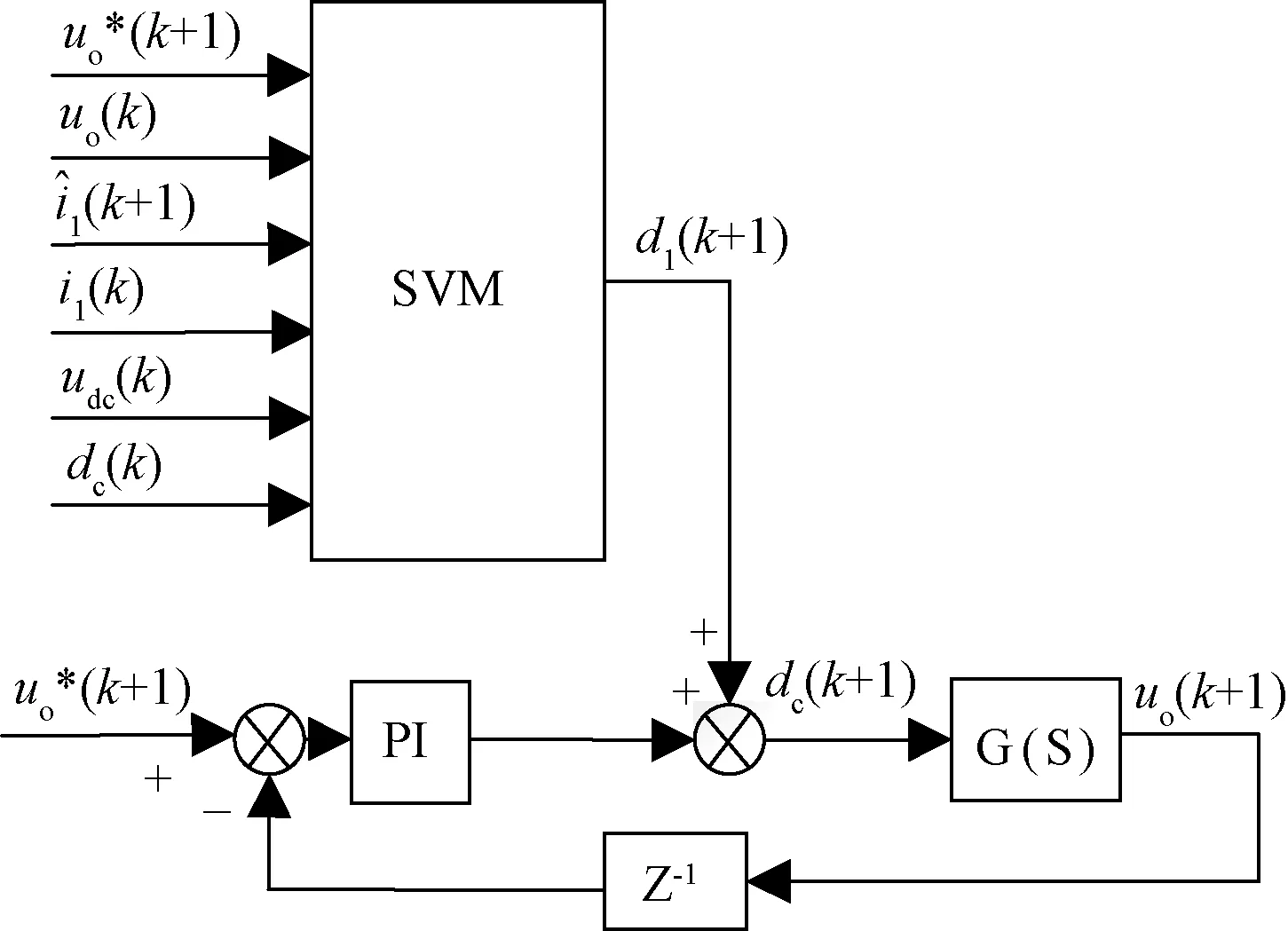
图3 支持向量机逆模型复合控制系统

2.4 训练样本的获取

要想建立准确的逆模型，首先要得到足够多的实验样本，这些样本必须体现逆变器的整体特性，保证样本数据可以覆盖逆变器工作的整个样本空间。因此需要充分的激励原系统，从而获得有效地训练样本。

搭建了3 kW的储能逆变器模型，为了保证样本的多样性，需采集逆变器不同工况下的数据，PWM占空比输入选取了不同幅值的正弦信号与随机信号叠加的设置，负载选用线性负载和非线性感性负载相切换，设置逆变器分别运行在25%，50%，75%以及100%的阻性负载和整流性负载的工况下。以25 kHz的采样频率进行数据采集，分别采样直流侧输入电压值udc、逆变器输出电压u0、电感电流i1、占空比信号d。

3 仿真与验证

3.1 样本采集与训练

借助MATLAB中Simulink工具箱搭建容量为3 kW的微型储能逆变器控制仿真模型如图4所示。各参数设置如下：线路及滤波器等效电阻R1=2 Ω，滤波电感L1=0.2 mH，滤波电容C2=12 uF，电压输入在350～450 V波动，输出电压频率50 Hz，采样频率25 kHz。逆变器的PWM输入和负载整流器的导通角按照不同工况设置。

图4 仿真模型搭建

模型运行后，采集了44 000组样本数据，涵盖逆变器不同工况下的特性。逆模型学习是在MATLAB环境下，调用了台湾大学林志仁等开发的LIBSVM软件包，并在此基础上采用粒子群算法优化了支持向量机的参数，设置粒子群体规模为20个，最大迭代次数为30次。迭代完成后，获得的群体最优值，即为所要获得的惩罚参数C=4.487，不敏感损失参数ε=0.02以及核参数γ=1.628。进化过程如图5所示。

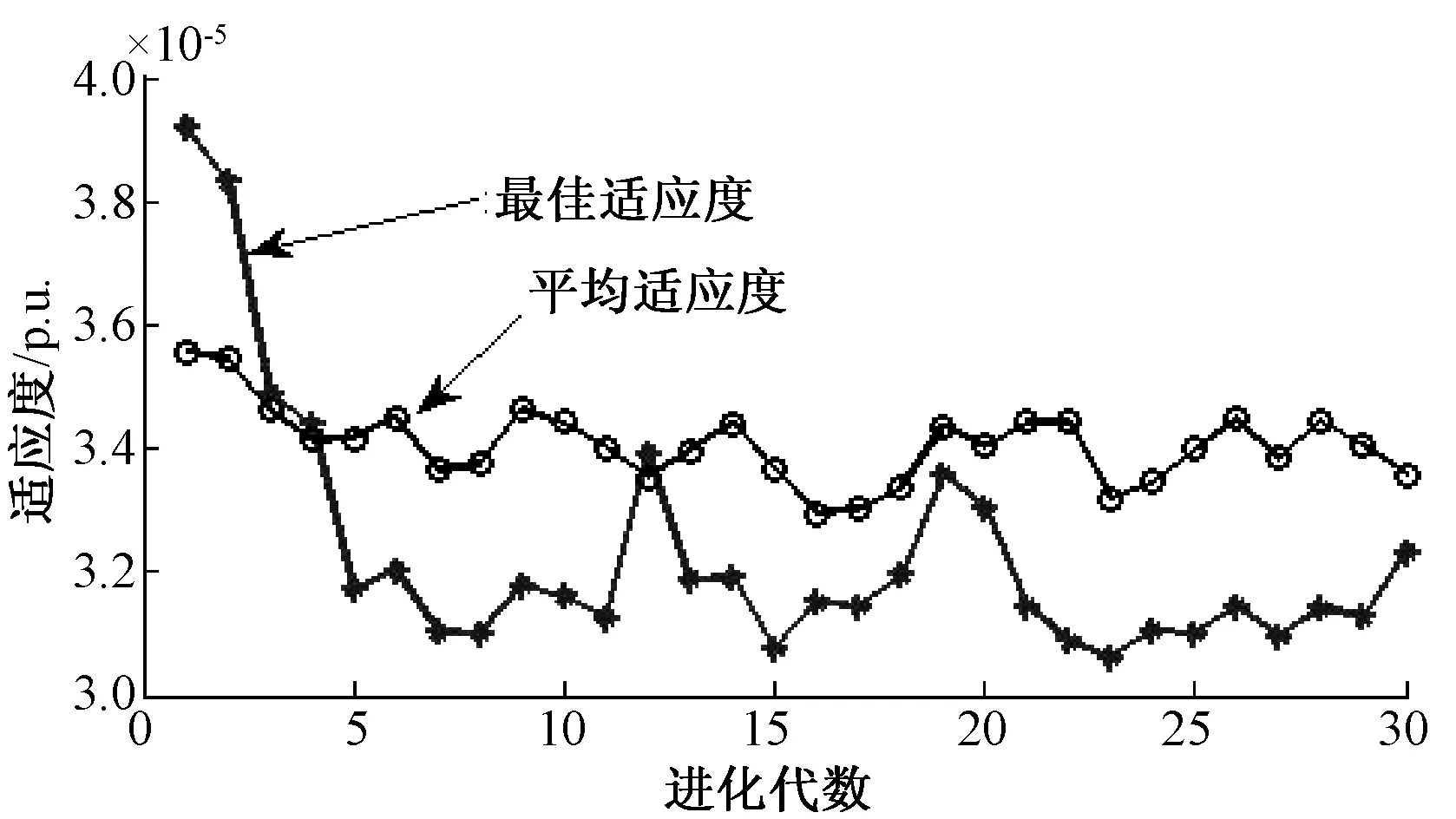
图5 PSO优化支持向量机迭代

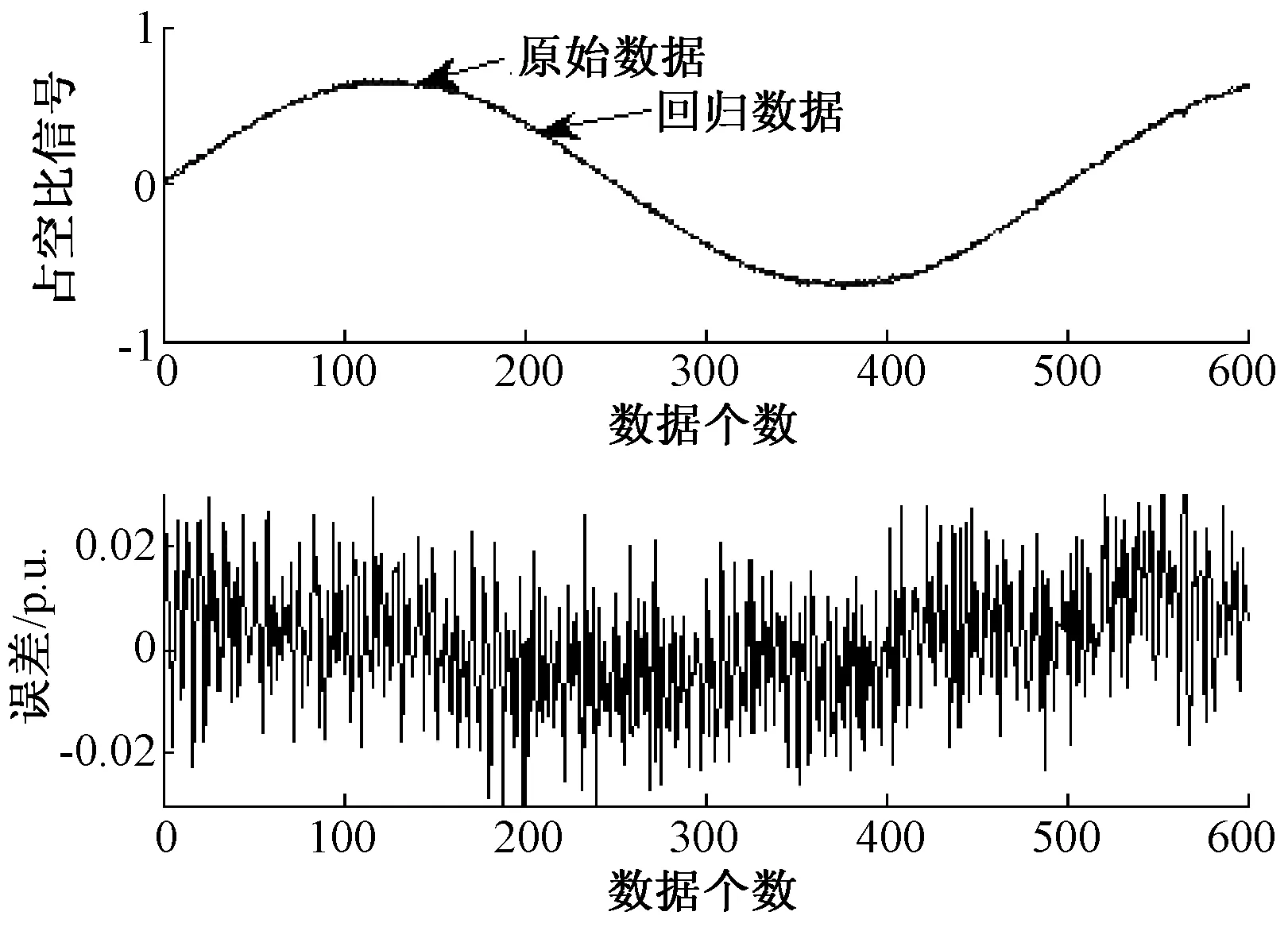
图6 支持向量机建模特性图

最终获得有效地支持向量634个，利用有效的支持向量，对采集的600组数据进行了验证，验证效果如图6所示，可以得出预测误差控制在了-0.02到0.02之间，验证了支持向量机逆模型预测的准确性。

3.2 SVM逆模型仿真

在Simulink中建立了逆变器SVM逆模型复合控制器如图7所示。

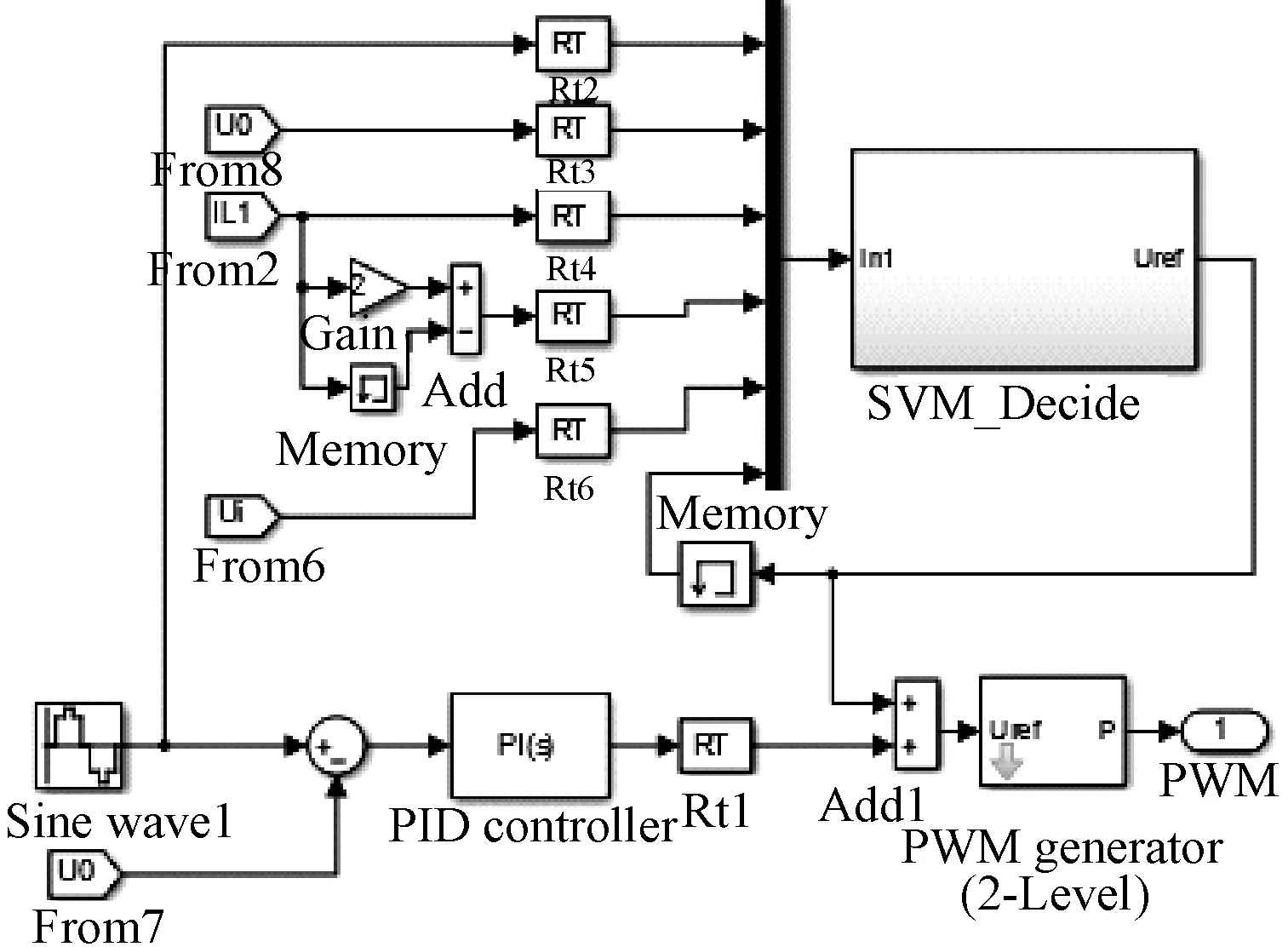
图7 复合逆控制器SPWM控制器

针对储能逆变器控制性能的测试，本文选取了整流性负载。整流性负载输出电流突变较大，再加上逆变器内部阻抗的存在，对输出电压波形影响较大，因此整流性负载下逆变器电输出电压质量可以反映出逆变器性能的好坏。

本文中分别采用了双闭环PI控制(控制参数为：电流内环kp=0.5，ki=10；电压外环kp=0.3，ki=20)，直接逆控制和支持向量机复合控制算法(控制参数：kp=0.4，ki=5)进行测试。电压给定为峰值为311 V频率为50 Hz的正弦波，整流桥采用全波可控整流，正负半波的导通和关断角分别为45°和135°。图8，9分别是整流性负载在50%和90%时电压电流波形(图中电流放大10倍)的情况，(a)是采用双闭环PI控制；(b)采用支持向量机直接逆控制；(c)采用支持向量机复合逆控制。其中整流性负载在50%和90%时电能质量参数如表1、2所示。

图8 50%整流负载下逆变器输出波形图

表1 50%整流性负载下电能质量参数

仿真结果表明，传统的双闭环PID控制，在负载较小时可以达到控制要求，但是负载增大后，PI的参数已经不适合当前负载，在整流负载晶闸管导通关断瞬间，逆变器输出端口电压波动较大，并且基波电压幅值达不到要求；采用支持向量机直接逆控制，电流的较大波动，也会影响逆变器的输出电压，引入较大量的谐波；而采用增加闭环的复合逆控制算法有效地补偿了电流的波动对端口电压的影响，电压谐波含量少，稳态误差小。

图9 90%整流负载下逆变器输出波形图

表2 90%整流负载下电能质量参数

4 结论

针对逆变器带整流负载难以控制的问题，提出了支持向量机复合逆控制的方案。利用SVM辨识逆变器系统的逆模型，再配合电压PI反馈控制完成对逆变器的电压波形的控制。从仿真实验可以得出，输出电压得到了有效地控制，畸变量较少，基波幅值与预期相近，进一步证明了该方案的可行性。

[1]孙晓明,刘涤尘,黄涌,等. 一种基于电源周期平均模型的单相PWM逆变器准PID控制器[J]. 中国电机工程学报,2006,26(24):50-54.

[2]王川川,朱长青,顾闯. 逆变器双环控制算法仿真研究[J]. 电子设计工程,2011,19(4):78-81.

[3]周娟,秦静,王子绩，等. 内置重复控制器无差拍控制在有源滤波器中的应用[J],电工技术学报,2013,28(2):233-238.

[4]陈礼恭. 单相光伏SPWM逆变器的重复控制策略研究[D].杭州：浙江工业大学,2013.

[5]唐贤伦. 群体智能与多Agent系统交叉结合——理论、方法与应用[M].北京：科学出版,2014.

[6]胡良谋,曹克强，等.支持向量机故障诊断及控制技术[M].北京：国防工业出版社.2011.10.

[7]马云龙.神经网络逆控制在单相光伏逆变系统中的应用研究[D].保定:华北电力大学,2015.

[8]李春来,刘卫亮,王印松，等. 基于FPGA的微网储能逆变器电压逆控制方案实现[J].电力科学与工程,2016，32(2):43-48.

[9]李浩然,杨旭红,冯成臣. 带LCL滤波器的并网逆变器双环控制参数设计研究[J]. 华北电力大学学报(自然科学版),2015,42(6):72-77.

[10]KENNEDY J,EBERHART R.C. Pariticle swarm optimization[C]//IEEE International Conference on Neural Networks, Piscataway, 1995: 1942 -1948.

[11]VAPNIK V N.The nature of statistical learning theory[M].New York:Springer,1995.

LI Jisen, LIN Yongjun, LIU Lili ,LIU Weiliang(School of Control and Computer Engineering，North China Electric Power University，Baoding 071003， China )

Energy Storage Inverter Control Strategy Based on Support Vector Machine

The current fluctuation of the energy storage inverter with nonlinear load is large in the micro grid operation, and the existence of output impedance existing in the output port cannot be ignored, which causes the control difficulty for the voltage waveforms of the output terminal. In this paper, a hybrid inverse control strategy based on support vector machine is proposed aiming at that problem. The particle swarm optimization algorithm is used to optimize the parameters based on the analysis of support vector machine. According to the related disturbance of the inverter output voltage, the inverse model structure of the inverter is constructed, and the inverse model of the support vector machine is trained by the data training of the energy storage inverter under different working conditions. In order to improve the control performance of the system, the output of the inverse model is used as the input of the energy storage inverter, and is combined with the output voltage feedback. The simulation results show that the proposed control strategy can improve the dynamic performance of the energy storage inverter and reduce the voltage harmonics as well.

energy storage inverter; inverse model; support vector machine; harmonic

2016-06-16。

中央高校基本科研业务费专项资金(2015ZD17)。

李继森(1990-)，男，硕士研究生，主要研究方向为新能源控制技术，E-mail：lijisen210@sina.com

TN743

A DOI:10.3969/j.issn.1672-0792.2016.09.009