弱链对角占优矩阵的逆矩阵无穷范数的新上界

蒋建新，李艳艳

（文山学院 数学学院，云南 文山 663000）

弱链对角占优矩阵的逆矩阵无穷范数的新上界

蒋建新，李艳艳

（文山学院 数学学院，云南 文山 663000）

研究了弱链对角占优矩阵A的逆矩阵无穷范数上界的估计问题，得到了A-1的元素的上界，结合该新上界得到了的新上界。数值算例说明新上界比潘淑珍、李艳艳的已有研究结果更精确。

弱链对角占优矩阵；M矩阵；逆矩阵；无穷范数；上界

对角占优矩阵是计算数学中应用非常广泛的矩阵类，它在信息论、系统论、现代经济学、网络、算法和程序设计等领域都有着十分重要的应用。对于对角占优矩阵中的弱链对角占优矩阵的逆矩阵无穷范数界的估计，1974年Shivakumar首先在文献［1］中给出了一些估计式。随后国内的许多学者对该问题进行了研究，得到了大量的不同估计式，可是这些结果大多数都依赖于A-1的元素［2-6］或者A与A-1的谱半径［7-8］等，计算时很不方便，2012年潘淑珍［9］在前人研究的基础上，得到了只依赖于A的元素的估计式。

本文在文献［9］的基础上，通过改变文献［9］中估计式中参数的取值，得到了只依赖于A的元素的新估计式，且新的结果比文献［9-10］中的估计式更精确。

1　预备知识

Cn×n（Rn×n）表示n阶复（实）矩阵集，N代表全体非零自然数的集｛1，2，…，n｝。

e=（1，1，…，1）T表示所有分量全为1的列向量。Zn=｛A=（aij）∈Rn×n|aij≤0，i，j∈N，i≠j｝。

A的无穷范数记为‖A‖∞，即

定义1［1］设A=（aij）∈Rn×n，若∀i∈N，有di≤1，J（A）≠∅，且∀i∈N，i∉J（A），有aii1ai1i2…airik≠0 i1≠i≠i2，…，ir≠ik，0≤r≤k-1，ik∈J（A），则称A为弱链对角占优矩阵。

定义2［1］设 A=（aij）∈Zn。若 A-1≥0，则称A为M矩阵；若∀i∈N，有aii＞0，则称A为L矩阵。

1974年P N Shivakumar［1］研究了弱链对角占优M矩阵A的逆矩阵A-1的元素及‖A-1‖∞的估计问题，并给出弱链对角占优M矩阵的‖A-1‖∞的上界

2012年潘淑珍在文献［9］中给出了此类问题的新上界，且该新上界改进了式（1）的估计。

其中ti由式（3）定义

对∀i，1≤i≤n-1，设A的主子矩阵为

若A为弱链对角占优M矩阵，则A（i，n）也为弱链对角占优M矩阵。

引理1［1］若A=（aij）∈Rn×n为弱链对角占优M矩阵，B=A（2，n）∈R（n-1）×（n-1），A-1=（αij），B-1=（βij）。则

引理2［1］若A=（aij）∈Rn×n为弱链对角占优M矩阵，A-1=（αij），则对∀i，j∈N，i≠j，有|αij|≤di|αjj|≤|αjj|。

引理3［2］若A=（aij）∈Rn×n为弱链对角占优M矩阵，且J（A）=｛i1，i2，…，ik｝，那么存在一个N的置换｛i1，i2，…，in｝，使得对所有的 j∈N，有

给出下列符号表示：

2　主要结果及证明

定理1若A=（aij）∈Rn×n为弱链对角占优M矩阵，n≥2，A-1=（αij），满足u1＜1，则

证明：因为A为M-矩阵，则A-1≥0，设Ah=x，其中h=（1，h1，…，h1）T，x=（x1，x2，…，xn）T，因为0≤h1≤1，

所以，x1＞0，xi≥0，（i=2，3，…，n）。再由A-1x=h，A-1≥0，有

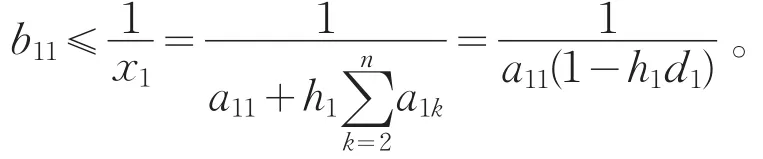
定理2设A=（aij）∈Rn×n是弱链对角占优M矩阵，n≥2，A-1=（αij），B=A（1，n），A-1=（αij），B-1=（βij），满足u1＜1，则

（Ⅱ）当2≤i≤n时，由定理1得αi1≤α11，

定理3设A=（aij）∈Rn×n是弱链对角占优M矩阵，对∀k∈N，满足uk＜1，则

3　数值算例

以上两例说明本文得到的结果是有效的，并且提高了文献［9-10］中的相应结果。

［1］SHIVAKUMAR P N，CHEW K H.A sufficient condition for nonvanishing of determinants［J］.Proceedings of the American Mathematical Society，1974，43（1）：63-66.

［2］HUANG T Z，ZHU Y.Estimation of‖A-1‖∞math container loading mathjax for weakly chained diagonally dominant M M math container loading mathjax-matrices［J］.Linear Algebra&ItsApplications，2010，432：670-677.

［3］王亚强，李耀堂，孙小军，等.严格对角占优M矩阵的‖A-1‖∞的上界的一个新估计式［J］.山东大学学报（理学版），2010，45（4）：43-48.

［4］杨晓英，曾宝国，朱清溢，等.严格对角占优M矩阵A的‖A-1‖∞上界的新估计式［J］.湖南师范大学学报（自然科学版），2014，37（3）：91-95.

［5］周平，李耀堂.M矩阵及其非负矩阵Hadamard积和Fan积的特征值界的估计［J］.云南大学学报（自然科学版），2012，34（1）：9-14.

［6］许洁，赵微，孙玉祥.广义对角占优矩阵的实用新判定［J］.云南大学学报（自然科学版），2014，36（5）：637-641.

［7］卢飞龙，何希勤.M-矩阵与其逆的Hadamard积的特征值下界［J］.辽宁科技大学学报，2010，33（5）：555-560.

［8］高美平.M-矩阵与其逆的Hadamard积的最小特征值下界新的估计式［J］.四川师范大学学报（自然科学版），2014（1）：90-97.

［9］潘淑珍，陈神灿.弱链对角占优矩阵‖A-1‖∞的上界估计［J］.福州大学学报（自然科学版），2012（3）：281-284.

［10］李艳艳，李耀堂.弱链对角占优矩阵的‖A-1‖∞的新界［J］.云南民族大学学报（自然科学版），2014，23（4）：259-261.

New Upper Bound for the Infinite Norm of the Inverse Matrix of a Weakly Chained Dominant Matrices

JIANG Jianxin，LI Yanyan
（Department of Mathematics，Wenshan University，Wenshan 663000，Yunnan，China）

The problem of estimating the bound of the infinite norm of the inverse matrix of a weakly chain diagonally dominant matrix is studied.The upper bound of the element ofA-1is obtained，combined with the new upper bound get the new upper bound of element of||A-1||∞.Numerical examples illustrate the new bound is more accurate than the estimation formula of Shuzhen Pan and Yanyan Li.

weakly chained diagonally dominant matrix；Mmatrix；Inverse matrix；infinity norm；Upper bound

O151.21

A

1672-2914（2016）02-0053-03

2015-09-15

文山学院科研基金项目（15WSY11）；文山学院重点学科项目（12WSXK01）。

蒋建新（1981—），男，甘肃天水市人，文山学院数学学院讲师，研究方向为矩阵理论及其应用。