一类奇异二阶微分方程的正解

张环环

（西北民族大学 数学与计算机科学学院，甘肃 兰州 730030）

一类奇异二阶微分方程的正解

张环环

（西北民族大学 数学与计算机科学学院，甘肃 兰州 730030）

在涉及相应线性微分方程第一特征值的条件下，通过构造一个适当的积分算子和特殊的锥，利用锥上的不动点理论，研究了一类奇异积分边值问题，允许非线性项在端点处具有奇性的情况下，得到了其正解的存在性。

正解；奇异边值问题；锥；不动点定理

常微分方程非局部边值问题的研究是研究微分方程理论及其应用的重要方向之一。非局部边值问题主要包括多点边值问题和积分边值问题。带有积分边界条件的常微分方程边值问题起源于对热传导和化学工程等问题的研究［1-3］。带有积分边界条件的边值问题包括两点、三点、m-点等非局部边值问题，关于这类问题正解的存在性、多解性及唯一性，得到了广泛的关注［4-7］。文献［6］利用锥中严格集压缩算子的不动点指数理论，研究了Banach空间中一类二阶微分方程积分边值问题正解的存在性。文献［4-5，7］在相应线性方程第一特征值的条件下，利用相关的不动点理论得到了某些微分方程正解存在性的较优结果。

近年来，对于奇异多点边值问题正解的研究引起了人们的广泛关注［1-3，6］。但以往所研究的非线性项f（t，x）关于t在端点0，1处具有奇性的情况，或者对非线性项 f（t，x）添加了较强的条件限制［2-3，8-9］。本文在相应线性方程第一特征值的条件下，利用锥拉伸压缩不动点定理研究非线性奇异微分方程积分边值问题

正解的存在性，本文允许w（t）在端点t=0，1处具有奇性，f（t，x）在x=0具有奇性。

1　预备知识

其中 fr，R（s）=sup｛f（s，x）|s∈I，x∈［rz（t），R］｝。

为了应用锥上的不动点定理，令：

则P为X中的锥。

注意到对∀u∈P｛θ｝，有u（t）＞0，t∈（0，1），因此如果u是问题（1）在P｛θ｝中的一个解，那么称u是问题（1）的一个正解。定义算子A:P｛θ｝→X如下：

再定义一个线性算子T:P→P，

由H（t，s）和G（t，s）的定义知，H（t，s）和G（t，s）有如下性质:

命题1对∀t，s∈［0，1］，G（t，s）≥0，∀t，s∈（0，1），G（t，s）＞0。

命题2∀t∈Iδ，s，τ∈I，G（t，s）≥z（t）G（τ，s），其中z（t）=min｛t，1-t｝，t∈Iδ。

证明：首先，z（t）=min｛t，1-t｝＜1，t∈Iδ，对任意的s，τ∈［0，1］，下面分情况讨论：

（Ⅰ）当max｛t，τ｝≤s时，

G（t，s）=1-s≥（1-s）z（t）=G（τ，s）z（t）；

（Ⅱ）当min｛t，τ｝≥s时，

G（t，s）=1-t≥（1-t）（1-τ）≥（1-τ）z（t）= G（τ，s）z（t）；

（Ⅲ）当t≤s≤τ时，

G（t，s）=1-s≥1-τ=G（τ，s）≥G（τ，s）z（t）；

（Ⅳ）当τ≤s≤t时，

G（t，s）=1-t≥（1-t）（1-s）=（1-t）G（τ，s）≥G（τ，s）z（t）。

于是命题成立。

命题4假设条件（H1）成立，则对

证明：对∀t∈Iδ，s，τ∈I，由命题2有

即命题4成立。

由条件（H1）（H2）及函数H（t，s）的性质知，由式（3）定义的算子A是有意义的。事实上对∀u∈P｛θ｝，有‖u‖≠0，且由式（2）知

从而由（H2）知

即由式（3）定义的算子A是有意义的。易知问题（1）在P｛θ｝中有解当且仅当u（t）=Au（t）在P｛θ｝中有不动点，并且问题（1）的正解等价于A的不动点。

其中Pr=｛u∈P|‖u‖＜r｝。

所以A:D→P。

下证A:D→P全连续。当n＞m0时，取

则wn（t）:［0，1］→［0，+∞）连续，并且wn（t）≤w（t），t∈（0，1）；再取

则fn（t，x）:［0，1］×［0，+∞）→［0，+∞）连续，并且fn（t，x）≤f（t，x）。令

易证An:D→P全连续，于是由式（5），（7）知∀ε＞0，∃m0，当n＞m0时，

这说明A可以由全连续算子列｛An｝一致逼近，所以P全连续。证毕。

引理2［8］设T:X→X是一个线性全连续正算子，若存在

满足λ1Tu0=u0（这里是T的谱半径），且使得对任给的u∈Q｛θ｝，都存在自然数n和实数α＞0，β＞0，满足αu0≤Tnu≤βu0，则对∀u∈Q，若u≠μu0（μ≥0），则必有λ1Tu≰u，λ1Tu≱u。

注：若条件（H1）（H2）满足，利用H（t，s）的性质及与引理1完全类似的证法可得由式（4）定义的算子T是一个全连续的正线性算子，令，则λ1为线性方程特征值问题

的第一特征值。

引理3［9］设P是实Banach空间X中的一个锥，0＜R1＜R2＜+∞，全连续，并且满足下列两条件之一。

为了方便本文再给出要用到的假设条件：

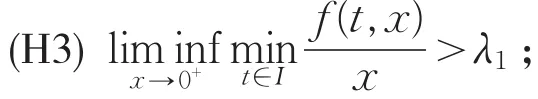
下面利用引理3，证明二阶奇异微分方程积分边值问题（1）正解的存在性与多解性。

2　主要结果及其证明

定理1假设条件（H1）-（H4）满足，则问题（1）至少存在一个正解。

证明：由条件（H3）知∃r1＞0和ε（0＜ε＜λ1），使得 f（t，x）≥（λ1+ε）x，∀t∈I，0＜x＜r1。验证

事实上，若存在 u1∈∂Pr1，使得 Au1≤u1，则对∀t∈I，有

即u1≥λ1Tu1，注意到u1（t）≥0，t∈I，从而由引理3知，存在μ≥0使得u1=μu0。若μ=0，则u1（t）≡0，这与‖u1‖=r1矛盾；若μ＞0，则

即u0≥（λ1+ε）Tu0，这与u0=λ1Tu0矛盾。从而式（8）成立。

由条件（H4）知 ∃R1＞r1和 ε（0＜ε＜λ1），使得f（t，x）≥（λ1-ε）x，∀t∈I，x＞R1。

事实上，若存在u2∈∂PR2，使得Au2≥u2，从而对∀t∈I，有

即u2（t）≤λ1Au2（t），t∈I。注意到u2（t）≥0，t∈I。从而由引理2知存在μ≥0，使得u2=μu0。若μ=0，则u2（t）≡0，这与‖u2‖=R2矛盾；若μ＞0，则μu0（t）=u2≤（λ1-ε）Tu2（t）=μ（λ1-ε）Tu0（t），即u0（t）≤（λ1-ε）Tu0（t），t∈I，这与u0（t）=λ1Tu0（t），t∈I矛盾。从而式（10）成立。

由式（8）（10），且根据引理1知算子A是全连续的，应用引理3可得A在中有不动点。证毕。

定理2假设条件（H1）-（H3）和（H5）（H6）满足，则问题（1）至少存在两个正解。

证明：由（H3）可知存在0＜r1≤Γ，当0＜x≤r1时，f（t，x）≥（λ1+ε）x，t∈I。由（H5）可知存在

与定理1的证法类似可证：

事实上对于∀u∈∂Pr2，，t∈Iδ。于是当z（t）r2＜u（t）≤r2≤r0（t∈Iδ）时，根据（H6）有

上式是矛盾的，从而Au≱u，∀u∈∂Pr2。

3　结论

本文在线性微分方程第一特征值的条件下，利用锥上的不动点理论，研究了一类二阶奇异积分边值问题，允许非线性项在端点处具有奇性的情况下，得到其正解的存在性。由于本文的条件和相应线性微分方程的特征值结合，并且对非线性项未作过多的限制，因此使得研究的函数类具有更广泛的意义。

［1］赵增勤.一类非线性奇异微分方程正解的存在性定理［J］.数学物理学报，2005，25A（3）：393-403.

［2］康平，刘立山.二阶奇异微分方程边值问题正解的存在性［J］.数学物理学报，2008，28A（1）：73-80.

［3］张兴秋.奇异二阶微分方程积分边值问题正解的存在唯一性［J］.系统科学与数学，2010，30（10）：1407-1416.

［4］崔玉军，孙经先.Banach空间中二阶微分方程三点边值问题的正解［J］.应用数学学报，2011，34（4）：743-751.

［5］LI Y X.Positive solutions of second-order boundary value problems with sign-changing nonlinear terms［J］.Journal of MathematicalAnalysisandApplications，2003，282：232-240.

［6］FENG M Q，JI D H，GE W G.Positive solutions for a class of boundary value problem with integral boundary conditions in Banach spaces［J］.Journal of Computational and Applied Mathematics，2008，222：351-363.

［7］LI Y H，LIANG Z P.Two positive solutions to three-point singular boundary value problems［J］.Acta Mathematica Scientia，2011，31B（1）：29-38.

［8］KRASNOSELSKII M A.Positive solutions of operator equations［M］.Groningen:Noordhoff，1964：48-105.

［9］郭大钧.非线性泛函分析［M］.济南：山东科学技术出版社，2001：78-151.

Positive Solutions to a Class of Singular Second-order Differential Equations

ZHANG Huanhuan
（College of Mathematics and Computer Science，Northwest University for Nationalities，Lanzhou 730030，Gansu，China）

By constructing an available integral operator and a special cone and using the fixed point theorems of cones，the existence of positive solutions for a class of singular boundary value problems with integral boundary conditions is investigated under some conditions concerning the first eigenvalue corresponding to the relevant linear problems，where the nonlinearity may be singular on boundary.The result presented here improves some recent results.

positive solution；singular boundary value problem；cones；fixed point theorem

O175.8

A

1672-2914（2016）02-0049-04

2015-11-11

数学天元基金项目（11326100）；中央高校基本科研业务费资助项目（31920130010）。

张环环（1980—），女，甘肃静宁县人，西北民族大学数学与计算机科学学院讲师，研究方向为非线性泛函分析及应用。