探讨命题之间的关系及运用

龚光剑

（广西右江民族商业学校，广西 百色 533000）

探讨命题之间的关系及运用

龚光剑

（广西右江民族商业学校，广西 百色 533000）

把握好命题知识点的内涵及运用，尤其是把握好四种命题之间的关系并灵活运用其来解决数学问题，有助于学生逐步学会推理、善于推理，提高学生的思维能力和解决实际问题的能力。

命题；关系；运用

在简易逻辑范畴里，命题是一个重要的知识点，而逻辑学主要是研究思维形式及其规律的一门基础性学科，逻辑学通常用数学的方法来研究一些问题，这些问题是属于形式逻辑范畴，同时逻辑学更注重于数学证明与公理方法的研究。逻辑学作为研究数学问题、解决数学问题的重要工具，把握好逻辑学范畴里命题这个知识点的内涵及灵活运用，尤其是把握好四种命题之间的关系并灵活运用其来解决数学问题，能帮助学生逐步学会推理、善于推理，从而提高学生的思维能力和解决实际数学问题的能力。探讨四种命题之间的必然联系，对于学生对数学的进一步学习，有很大意义。

1 命题以及命题之间的关系

（1）判断一件事情正确与否的语句叫做命题，命题分为真命题和假命题，正确的命题叫真命题，错误的命题叫假命题。

（2）在两个命题中，如果第一个命题的题设（或条件）是第二个命题的结论，并且第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题；若把其中一个命题叫做原命题，则另一个命题叫做该原命题的逆命题。

（3）既否定原命题的条件，又否定原命题的结论，这样的命题叫原命题的否命题。

（4）把原命题的条件和结论交换位置，同时对原命题的条件和结论予以否定，这样的命题叫原命题的逆否命题。

（5）若用p原命题的条件，q表示原命题的结论。用¬p和¬q 分别表示p和q的否定，于是有原命题：若p则q；逆命题：若q则p；否命题：若¬p则¬q；逆否命题：若¬q则¬p。

（6）四种命题之间的关系

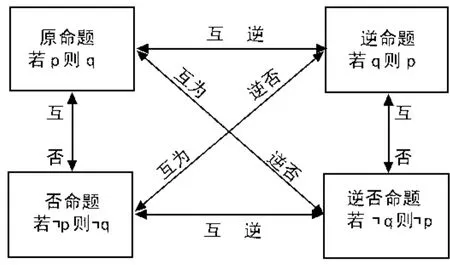
图1 四种命题之间的关系图

（7）四种命题之间的真假关系

表1 四种命题之间的真假关系表

2 灵活运用命题知识解决问题

2.1 已知一个命题，写出其另外三种命题

（1）要写出一个命题的逆命题、否命题和逆否命题，只要根据定义把命题的条件和结论进行否定或交换就可以了。

（2）如果命题不是“若p则q”形式，要写出其它三种命题，要先把该命题改写成“若p则q”的形式，然后再按（1）的方法来解决。

（3）若已知命题有大前提，则必须保留该命题的大前提。

（4）有几个条件组成的命题，应把其中一个（或几个）条件作为大前提。

如：N＜0，X，Y∈R，“若X＞Y则XN＜YN”的逆命题是“若XN＜YN则X＞Y”；否命题是“若X≤Y则XN≥YN”；逆否命题是“若XN≥YN则X≤Y”。

上述三种命题的大前提都是X，Y∈R，且N＜0，不能作任何改变。

2.2 区分好命题的否定形式和否命题

（1）区别。从概念上讲，命题的否定形式就是直接对命题的结论进行否定，而否命题却是原命题的条件和结论分别否定后组成的命题。从构成上讲，对于“若p则q”形式的命题，它的否定命题为“若p则¬q”，也就是不改变条件，只是否定结论而已；而其否命题则为“若¬p则¬q”，即对其条件和结论都进行否定。从真值上讲，否定命题的真值和原命题相反，而否命题的真值与原命题没有关系。

（2）联系。其一它们都是否定了原命题的条件或结论后组成的新命题；其次它们在否定的时候，对其正面叙述的词语的否定表达都是一样的。

2.3 灵活运用反证法

（1）反证法的思维程序。先否定问题结论——推理过程中引出矛盾（与假设相矛盾，或与题设相矛盾，或与定义、公理、定理、公式相矛盾，或自相矛盾）——从而肯定结论。

（2）反证法比较适合解决的问题。其一是命题很简单，没有更多公理概念等依据可供使用的命题；其二是结论本身以否定形式出现的一些命题；其三是命题的结论是以“至少…”或“至多…”的形式出现；其四是关于唯一性、存在性的命题；其五是结论的反面比原结论还具体、还容易研究和掌握。上述题型比较适合用反证法证明，但并不是一定要用反证法证明，也并不是说其它题型不能用反证法证明。

所以n²=2m²

因为n，m为互质

所以n，m均为奇数或n，m一奇一偶

但是n，m均为奇数或n，m为偶数，n为奇数n²=2m²均不成立；当m为奇数，n为偶数时，不妨设n=2k，则m²=2k²，这与m是奇数矛盾。

2.4 运用逆否证法证明数学问题

（1）逆否证法的定义。因为原命题与其逆否命题是等价的，所以如果要证明或判断原命题很困难的时候，就要考虑改成证明它的逆否命题成立，这种方法同样能够证明原命题，这种证明方法称为逆否证法。

（2）反证法与逆否证法的联系。其一都是利用原命题与其逆否命题的等价性，依据一样；其二都是从“¬q”（即否定结论）入手，起步相同；其三都是“正难则反”思想的具体体现，思想相同。

（3）反证法与逆否证法的区别。首先为目的不同，反证法否定结论的目的是为了推出矛盾，而逆否证法否定结论的目的是为了推出“¬q”。其二是本质上的不同，逆否证法实际上是证明一个新命题的成立，而反证法则是把否定的结论作为新的条件加上原有的条件进行逻辑推理，最终推出矛盾，从而肯定原命题是正确的。

例如：已知：有10个人去分56个水果，每人至少分到1个水果，至多分到10个水果。

求证：至少两个人分到的水果数一样多。

证明：假设没有两个人分到的水果一样多，则每人分到的水果数都不相同。只能为1，2，3，4，5，6…，10。这样共分掉1+2+3+4+5+6…+10=55个水果，与已知分掉56个水果这个条件矛盾，所以假设不成立，原结论正确。

再如：已知：x+y+z〉0，xy+yz+zx〉0，xyz〉0.

求证：x〉0，y〉0，z〉0。

［证明］：假设x，y，z不都是正数，那么由xyz〉0可知，这三个数中必有两个为负数，一个为正数。

不妨设x〈0，y〈0，z〉0，则由x+y+z〉0，

可得z〉-（x+y），

又x+y〈0，

∴z（x+y）〈-（x+y）（x+y）

xy+z（x+y）〈-（x+y）（x+y）+xy

即xy+yz+zx〈-x2-xy-y2

∵x2〉0，xy〉0，y2〉0，

∴-x2-xy-y2=-（x2+xy+y2）〈0，

即xy+yz+zx〈0，

这与已知xy+yz+zx〉0矛盾，

所以假设不成立.

因此x〉0，y〉0，z〉0成立。

总之，逻辑学是一门非常重要的学科，而四种命题知识点是逻辑学里至关重要的内容，在很多领域都有广泛的运用，在解决实际问题的过程中四种命题的知识点显得更为重要。对于四种命题的内涵理解和灵活运用，需要精心去探索、仔细去总结，并在灵活运用中不断总结提高和创新拓展，才能让命题这个知识点真真正正为学习数学知识和解决实际数学问题提供更多帮助。

To explore the relationship between propositions and application

Grasp the connotation of propositional knowledge and application， especially the grasp of the relationship between the four propositions and flexible use it to solve mathematical problems， help students to gradually learn to reasoning， be good at reasoning，improve the students' thinking ability and the ability to solve practical problems.

Proposition； relationship； using

O14

Α

1008-1151（2016）06-0109-02

2016-05-06

龚光剑（1976-），男，广西百色人，广西右江民族商业学校高级讲师。