基于逐点插入法生成Voronoi图的算法研究及实现

张　艳，李　强

(中国矿业大学(北京) 地球科学与测绘工程学院，北京 100083)



基于逐点插入法生成Voronoi图的算法研究及实现

张艳，李强

(中国矿业大学(北京) 地球科学与测绘工程学院，北京 100083)

基于逐点插入法生成Voronoi图需要首先生成Voronoi对应的Delaunay三角剖分，为满足大量离散点数据快速构建Voronoi图的效率需求，研究利用Lawson算法在形成三角网过程中进行LOP优化，快速生成可靠的Delaunay三角网，并应用Delaunay三角网与Voronoi图互为对偶的关系，构建所需的Voronoi图。在对大量的随机离散数据进行试验，并与标准的结果进行对比后发现，除部分异常情况，利用该算法可以快速准确地构建出目标Voronoi图。

Delaunay三角剖分；LOP优化；Voronoi图；逐点插入法

Voronoi图又称泰森多边形或者Dirichlet图，它在求解点集或者其他几何对象与距离有关的问题时有着重要的作用，应用领域从几何重构到计算机图形学、图像处理，从路径规划到粒子微观状态分布，几乎涵盖了自然科学领域的大部分学科[1-4]，由于它的广泛适用性，人们研究得出了一系列关于它的有效算法。

关于Voronoi的算法大致可以分为两类[5-6]：一是直接法，即直接由点集生成Voronoi图，比如半平面法、增量构造法、分治法、平面扫描线法等；二是间接法，利用Voronoi 图与 Delaunay 三角网互为对偶图的关系，先对点集剖分生成 Delaunay 三角网，然后构建Voronoi 图。关于间接法的研究有任永功等人的利用类Delaunay三角网实现Voronoi图[7]，刘少华等人的基于Delaunay三角网的泰森多边形生成算法研究[8]，卓中文等用炮孔取样点的数据作为数据源来研究基于Delaunay三角网生成Voronoi爆破图[9]，孙继忠等人针对Delaunay三角网生长算法和间接生成Voronoi图算法构网效率不高的问题，提出了一种基于Delaunay三角网间接生成Voronoi图的改进算法[10]。

逐点插入法是目前生成Delaunay 三角网应用最广泛的算法之一，该算法实现简单，易于推广到三维情况。本文基于逐点插入法进行Delaunay 三角剖分，再由Delaunay 三角网的对偶图成功地得到相关点集的Voronoi图[11-14]。

1　构建Voronoi步骤

算法实现的关键是对离散点进行合理的剖分，使之连接形成Delaunay 三角网，基本步骤如下：

1)构建Delaunay 三角网，对离散点和形成的三角形编号，记录每个三角形是由哪3个离散点构成的；

2)找出与每个离散点相邻的所有三角形的编号，并记录下来。只要在已构建的三角网中找出具有一个相同顶点的所有三角形即可；

3)对与每个离散点相邻的三角形按顺时针或逆时针方向排序；

4)计算每个三角形的外接圆圆心，并记录之；

5)根据每个离散点的相邻三角形，连接这些相邻三角形的外接圆圆心，得到Voronoi图。

2　Delaunay 三角网的构建

Delaunay 三角剖分对数值分析以及图形学来说，是极为重要的一项预处理技术，它有最大化最小角，即“最接近于规则化的”三角网和唯一性，任意四点不能共圆两个特点。

Delaunay剖分的生成算法主要有分治算法、逐步插入法、三角网生长法等。而逐点插入法的代表算法为1977年由Lawson提出的Lawson算法，该算法思路简单，易于编程实现[15]。基本原理为：

1)构造一个超级三角形，包含所有散点，放入三角形链表。

2)将点集中的散点依次插入，在三角形链表中找出外接圆包含插入点的三角形(称为该点的影响三角形)，删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，完成一个点在Delaunay三角形链表中的插入，如图1所示。

3)对局部新形成的三角形进行LOP优化，并将形成的三角形放入Delaunay三角形链表。

4)循环第二步，直到所有离散点插入完毕。

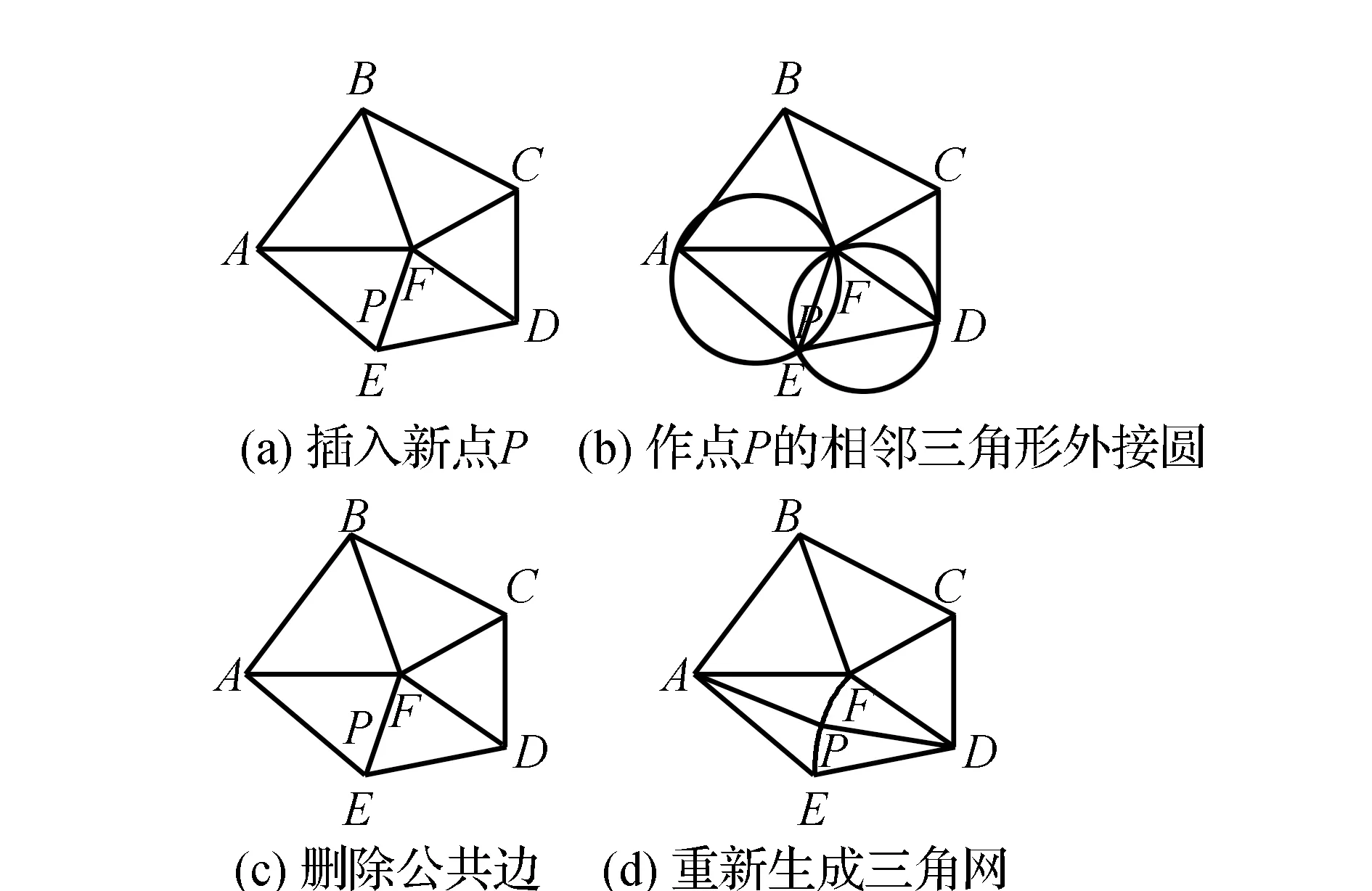
图1　插入新点后过程

3　算法流程及实现

3.1Delaunay三角剖分的生成

Lawson三角剖分算法的关键是先创建包含点集的凸壳，在插入新点后快速生成新的三角网，并进行LOP优化，得到Delaunay三角网。采用面向对象的方法实现程序的设计过程可以直观明朗地获取相关点、边、三角形的信息。

3.1.1初始设置

1)点类和点列表：Class Point and class PointList；

2)边类和边列表：Class Edge and class EdgeList；

3)三角形类和三角形列表：class Triangle and class TriangleList。

3.1.2数据读入

采用FileStream类，以文件流的形式读入数据，数据采用X，Y坐标形式，并利用GDI画图展点。

3.1.3建立凸壳

将数据存入点列表PointList，遍历最大最小的X，Y坐标值，用获取的最大最小横纵坐标值定义超三角形SuperTriangle的3个顶点坐标。

3.1.4生成Delaunay三角网

根据两点构成边，三边构成三角形的原理，首先构建点列表，由点列表得到边列表，再由边、点列表得到相应的三角形链表，最终按照Lawson算法得到Delaunay三角网，效果如图2所示。

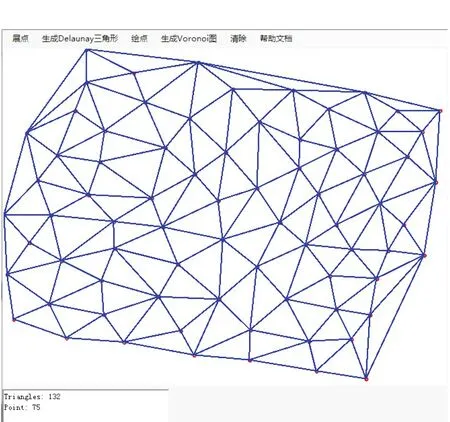
图2　75点生成的Delaunay三角网

3.2Voronoi图的构建

根据Voronoi图与Delaunay三角网互为对偶图的关系，在以生产Delaunay三角剖分的基础上可以迅速地得到相应的Voronoi图。

3.2.1初始设置

1)Voronoi图点列表：VPoint；

2)三角形边列表：VEdgeList；

3)三角形列表：TriangleList；

4)边另一点列表：OtherPointList。

3.2.2程序步骤

第一步：根据在Delaunay三角剖分过程中得到的三角形顶点列表，除去超级三角形顶点，然后依次将剩余点添加到新的VPoint列表。

第二步：遍历三角形边列表EdgeList，重新加入到VEdgeList边列表，并同时去除重复的边。

第三步：遍历VPoint列表，对每一点遍历该点相关的边列表VEdgeList，在这一过程中，同时记录边列表相关的另一点及其坐标值，并将该点即OtherPoint存入OtherPointList。

第四步：对OtherPointList内的点按逆时针排序，计算这些点相关的三角形外接圆圆心，并连接外接圆圆心，得到Voronoi图。最终效果如图3所示。

图3　生成的Voronoi图

4　结束语

根据逐点插入法进行Delaunay三角剖分得到Delaunay三角网是一种最为简洁快速的方法，避免了诸如分治法等算法的复杂性，尽管时间耗费相对加长，但现代计算机的进步完全弥补了这一缺陷。经本实验验证，由逐点插入生成Delaunay三角网，进而生成Voronoi图的方法切实可行。

[1]刘金义,刘爽.Voronoi图应用综述[J].工程图学学报,2004,25(2): 125-132.

[2]俞亚磊.GIS中Delaunay三角网与Voronoi图的相关问题研究[D].芜湖:安徽师范大学,2013.

[3]鲍蕊娜.离散点生成不规则三角网算法研究及实现[D].昆明:昆明理工大学,2012.

[4]纪志浩,于明旭.基于点云数据三维重建方法的研究[J].黑龙江工程学院学报,2014(3):7-9.

[5]宗大伟.Voronoi图及其应用研究[D].南京:南京航空航天大学,2006.

[6]袁子薇.Voronoi图细分算法研究[D].杭州:浙江工业大学,2013.

[7]任永功,廖士中.利用类Delaunay三角剖分实现Voronoi图[J].计算机科学,2002,29(9):78-79.

[8]刘少华,罗小龙,何幼斌,等.基于Delaunay三角网的泰森多边形生成算法研究[J].长江大学学报,2007,4(1):10-103.

[9]卓中文,王山东,魏生文,等.基于Delaunay三角网生成Voronoi爆破图的研究[J].现代矿业,2011(12): 106-108.

[10]孙继忠,胡艳,马永强.基于Delaunay三角剖分生成Voronoi图算法[J].计算机应用,2010,30(1):75-77.

[11]沈璐,宋晓东,邓宇.VC 环境下Delaunay 三角剖分算法的设计及实现[J].吉林建筑工程学院学报,2012,29(6):46-48.

[12]刘云,夏兴东,黄北生.基于分治算法与逐点插入法的Delaunay三角网建立算法的改进[J].现代测绘,2010(4):14-16.

[13]郭晓东.Delaunay三角形网络逐点插入法的优化算法[J].气象与环境科学,2014,37(2):112-116.

[14]王龙浩,王解先.基于逐点插入法的Delaunay三角网快速生成算法[J].工程勘察,2013,10:75-79.

[15]毕硕本,陈东祺,颜坚,等.基于二维凸壳的平面点集Delaunay三角网算法[J].计算机科学,2004,41(10): 317-320.

[责任编辑：郝丽英]

Research and implementation of Voronoi diagram generation algorithm based on point by point insertion method

ZHANG Yan，LI Qiang

(College of Geoscience and Surveying Engineering,China University of Mining & Technology,Beijing 10083,China)

Based on point by point insertion method,the Voronoi diagram needs to generate the Delaunay triangulation first in order to meet the efficiency requirement of constructing Voronoi diagram quickly with a number of discrete point data.In the paper Lawson algorithm is used to carry on the LOP optimization in the process of forming a triangulation network to generate a reliable Delaunay triangulation.The relation of mutual duality between Delaunay triangulation and Voronoi diagram is used to construct the desired Voronoi map.After testing a number of random discrete data and comparing with the results of the standard result,this paper obtains a result that in addition to some abnormal conditions,this algorithm can quickly and accurately frame the targetted Voronoi map.

delaunay triangulation; LOP optimization; Voronoi diagram; incremental insertion algorithm

10.19352/j.cnki.issn1671-4679.2016.05.007

2016-03-28

张艳(1991-)，女，硕士研究生，研究方向：煤矸石山温度场探测.

TP301.6

A

1671-4679(2016)05-0022-03