水文设计值置信区间估计研究

梁　骏，宋松柏

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)



水文设计值置信区间估计研究

梁骏，宋松柏

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

【目的】 研究给定设计标准下水文设计值置信区间的估算方法，评定设计值的不确定性。【方法】 以陕西省关中地区4个气象测站年降水量为例，选用矩法(MOM)和极大似然法(ML)研究P-Ⅲ分布水文设计值的置信区间计算方法，计算出不同设计频率下水文设计值在95%置信水平下的置信区间，并对基于矩法和极大似然法估算的设计值置信区间的长度数据进行比较分析。【结果】 在设计频率为0.2%时，周至、临潼、蓝田、户县4个测站采用极大似然法估算在95%置信水平下的设计值置信区间长度分别为414.28，338.88，360.65和371.24，采用矩法估算在95%置信水平下的设计值置信区间长度分别为546.61，435.64，384.91和403.92。在设计频率为99%时，上述4站采用极大似然法估算在95%置信水平下的设计值置信区间长度分别为144.44，124.93，177.67和160.73，采用矩法估算在95%置信水平下的设计值置信区间长度分别为183.28，151.26，187.31和178.62。由此可知，在低设计频率和高设计频率时，极大似然法估算的设计值置信区间长度均较矩法小。【结论】 置信区间能够为设计值的估算提供相对可靠的变化范围，用极大似然法估算水文设计值的置信区间比矩法能更有效地降低水文设计值的不确定性。

水文设计值；设计标准；标准差；置信区间；关中地区

水文现象是一种受气候、气象、地形、地貌和下垫面等因素影响的复杂自然现象，蕴含着确定性的动态规律和不确定性的统计规律。由于水文现象的极端复杂性以及人类认识水平的限制，使得对水文过程的认识存在着不确定性[1]。为了描述和减少水文事件的不确定性问题，目前国内外大都是采用数理统计方法，通过对历史实测资料进行分析，从而揭示水文现象的统计规律，从概率的角度定量预估研究区未来可能的水文情势。预测水文极值事件发生的频率和大小对整个社会具有非常重大的意义。在水利工程的防护工作和警示系统中，采用频率分析能够减少或者消除由于暴雨和洪水引起的生命财产损失。减少估计误差及降低不确定性的影响从而得到比较合理的预估结果，以及对成果进行合理性分析，是水文分析计算的重要内容，因此需要特别重视[2]。对于一个设计师或者工程师而言，量化水文设计值不确定性是非常有必要的[3]。实际中，有两种方法用来描述水文设计值估算的不确定性程度，即标准误差和置信区间，其中设计值的标准误差用于描述由样本估算的设计值与真设计值(真设计值未知)之间的偏离程度，样本估算设计值的置信区 间则描述了给定概率下真设计值的取值区间。点估计及其标准差是对一个参数真实值的不确定性描述，除非知道问题中有关参数估计值的分布[4]。对于一个点估计及其标准误差来说，置信区间能够提供更多的信息。

20世纪60年代起，国外有学者提出了一些水文设计值置信区间的计算方法[5-10]，而国内在这方面的研究相对较少，缺乏不同参数估算方法相应置信区间的对比。目前用于水文频率计算中的分布线型已多达十余种，但仍然无法知道水文随机变量概率分布的确切线型，我国水利水电工程水文计算规范中推荐采用的是P-Ⅲ型分布。因此，本研究采用矩法和极大似然法进行参数估算，以陕西省关中地区降水资料为例，选用P-Ⅲ型概率分布,用矩法和极大似然法两种参数估算方法进行水文设计值的置信区间估算，度量水文设计值的不确定性，以期为水文设计值的估算提供相对可靠的计算依据。

1　水文设计值置信区间

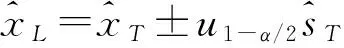
(1)

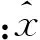
式(1)表明，为了得到水文设计值置信区间，需要先计算出水文设计值的近似方差或均方差 。

2　基于矩法估算设计值的近似方差

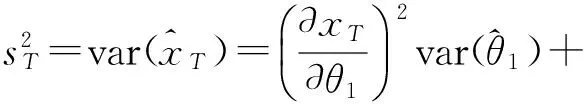
(2)

水文频率计算中，可以将水文设计值[13]表示为频率分布参数的函数形式，即：

(3)

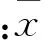
由式(2)、(3)知水文设计值的近似方差公式为：

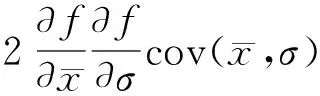
(4)

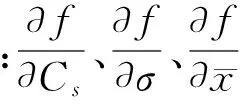
应用方差与数学期望值间的关系，经数学推导可得原点矩、中心矩的方差和协方差公式分别为：

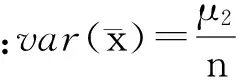
(5)

式中：n为样本序列长度，μ2为2阶中心矩，其余符号意义同上。

(6)

式中：vr为r阶原点矩，v2r为2r阶原点矩。

(7)

式中：vs为s阶原点矩，vr+s为r+s阶原点矩。

(8)

式中：μr为r阶中心矩，μ2r、μr-1、μr+1分别为2r阶、r-1阶、r+1阶中心矩。

(9)

式中：μs为s阶中心矩，μr+s、μs-1、μs+1分别为r+s阶、s-1阶、s+1阶中心矩。

原点矩与中心距的协方差:

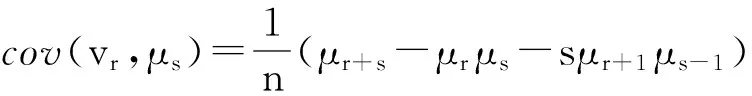
(10)

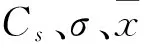
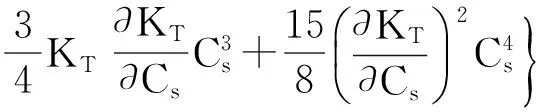
(11)

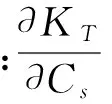
KT的近似计算可以采用Wilson-Hilferty变换公式[14]，有：

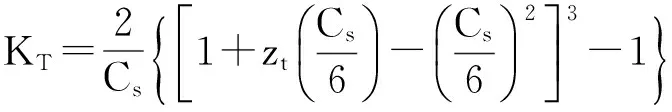
(12)

式中：zt为标准正态分布中对应于不超越概率(P=1-1/T)的分位数。

通过式(12)推导KT对Cs的偏导计算公式，在给定设计频率p下，得到离均系数KT以及KT对Cs偏导的近似值，连同矩法公式得到的样本序列特征值一起代入式(11)，求出基于矩法估算的水文设计值的近似方差，从而可由式(1)求出给定置信水平下水文设计值的置信区间。

3　基于极大似然法估算设计值的近似方差

P-Ⅲ型分布的密度函数为：

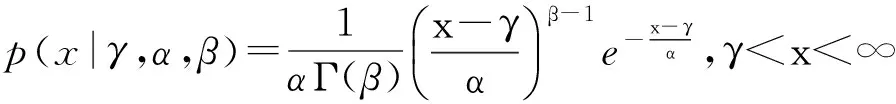
(13)

式中：γ为位置参数，α为尺度参数，β为形状参数，Γ(β)为gamma函数。

根据水文统计原理，有似然函数：

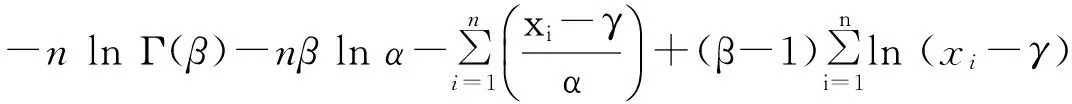
(14)

式中：xi是样本序列第i个值，lnL为对数似然函数。

式(14)对数似然函数分别对α、β、γ求偏导数，并令相应的偏导数值为0，求解非线性方程组即可获得参数α、β、γ的估算值。极大似然法推求参数过程比较麻烦，计算时可以使用优选法、查数值表法和MATLAB软件编程法得到3个分布参数的估计值[15]。本研究使用MATLAB软件编程，将通过矩法求出的分布参数估算值作为初值，迭代后得到满足似然方程为0条件的分布参数α、β、γ。

由P-Ⅲ型分布的性质[16]，有：

E(x)=αβ+γ；var(x)=α2β。

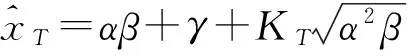
(15)

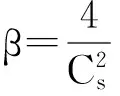
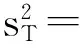
(16)

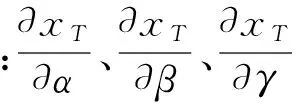
由式(16)可知，需要先计算出P-Ⅲ分布中参数的方差和协方差。

方差-协方差矩阵U是Fisher信息矩阵I的逆矩阵。信息矩阵的元素等于似然函数关于分布参数二阶偏导数的数学期望。方差-协方差矩阵为：

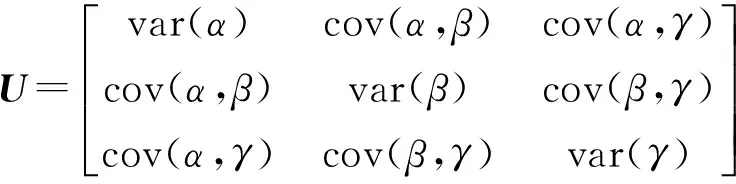
(17)

信息矩阵为：

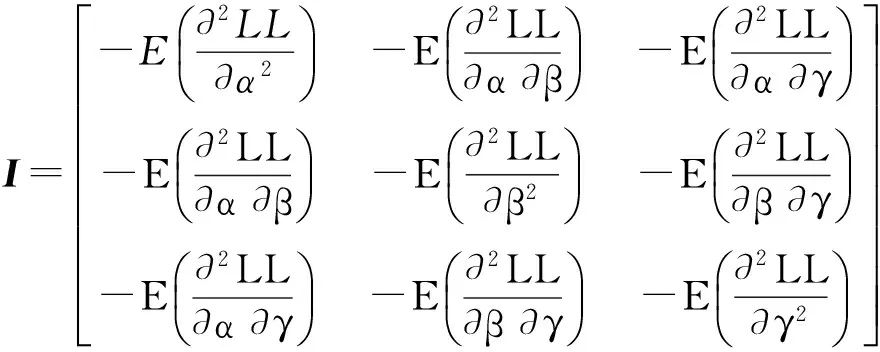
(18)

式中：L是P-Ⅲ型分布的密度函数的似然函数，var(α)、cov(α,β)等意义同上。

利用似然函数对分布参数二阶偏导数求期望，则信息矩阵转化为:

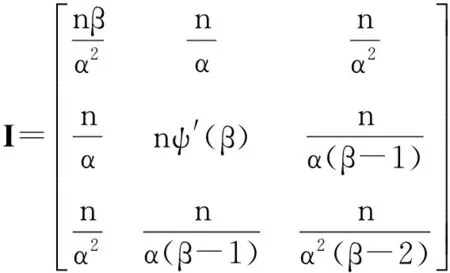
(19)

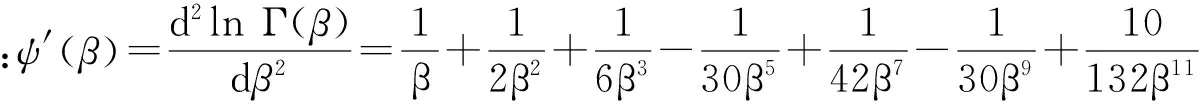
对式(19)中矩阵求逆，因为方差-协方差矩阵是信息矩阵的逆矩阵，则有：

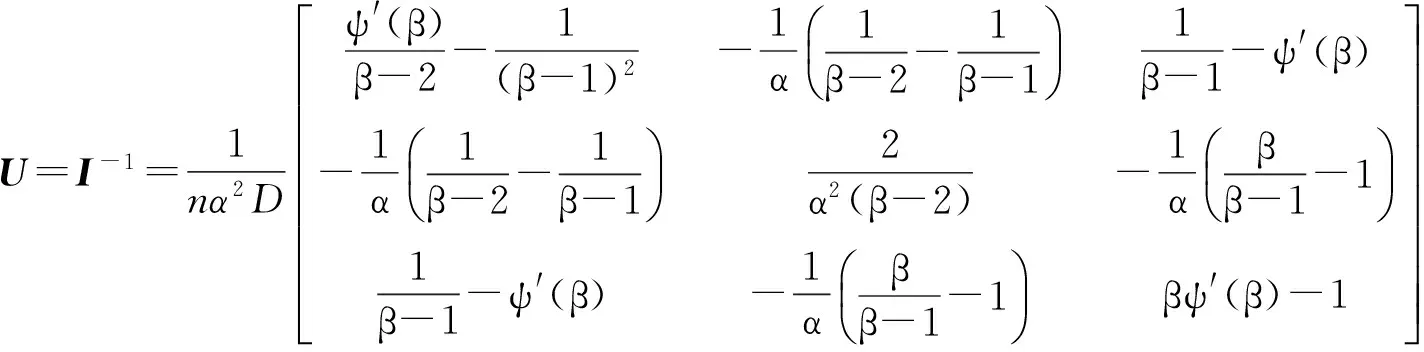
(20)

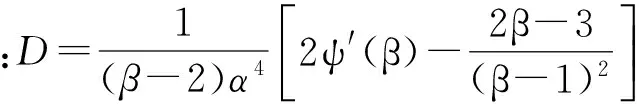
将上述通过极大似然法求得的分布参数值代入式(20)得到化简后的方差-协方差数值矩阵，连同离均系数 (计算方法同矩法)一起代入式(16)，可以求出极大似然法估算参数的水文设计值近似方差，从而可由式(1)求出给定置信水平下水文设计值的置信区间。

4　实例应用

以陕西省关中地区周至(1957-2008年)、临潼(1959-2008年)、蓝田(1959-2008年)、户县(1959-2008年)4个气象测站年降水量序列为例，选用P-Ⅲ型分布函数作为降水量频率分布模型，分别应用矩法(MOM)和极大似然法(ML)进行模型参数估算，利用上文讲述的公式计算不同设计频率下各站年降水量估算值及其在95%置信水平下的置信区间，结果见表1～4。由表1～4可知，关中地区周至、临潼、蓝田和户县4个测站年降水量资料选用P-Ⅲ分布作为模型分布时，采用矩法和极大似然法估算的设计值在95%置信水平下的置信区间有如下规律：置信区间的长度随着设计频率的减小(设计标准的提高)有一个先窄后宽的变化。中间段频率的置信区间长度最窄，往低频段和高频段，区间长度逐渐变大；在低设计频率段，设计值的置信区间长度都大于中高设计频率段设计值的置信区间长度，表明设计频率越低，设计值的不确定性程度越高。实际工作中，通常需要计算低设计频率和高设计频率(即频率曲线的高尾部和低尾部)的水文设计值，为水利工程的规划、设计和管理提供依据。通过比较基于矩法和极大似然法估算的设计值置信区间长度，无论在低设计频率还是高设计频率，4个测站均是采用极大似然法估算的设计值的置信区间长度较小，说明采用极大似然法估算设计值的置信区间比矩法能更加有效地降低水文设计值的不确定性。

表 1　周至站不同设计频率下年降水量设计值及其在95%置信水平下的置信区间Table 1　Annual precipitation quantile estimation and its 95% confidence interval under different design frequencies in Zhouzhi station　mm

表 2　临潼站不同设计频率下年降水量设计值及其在95%置信水平下的置信区间Table 2　Annual precipitation quantile estimation and its 95% confidence interval under different design frequencies in Lintong station　mm

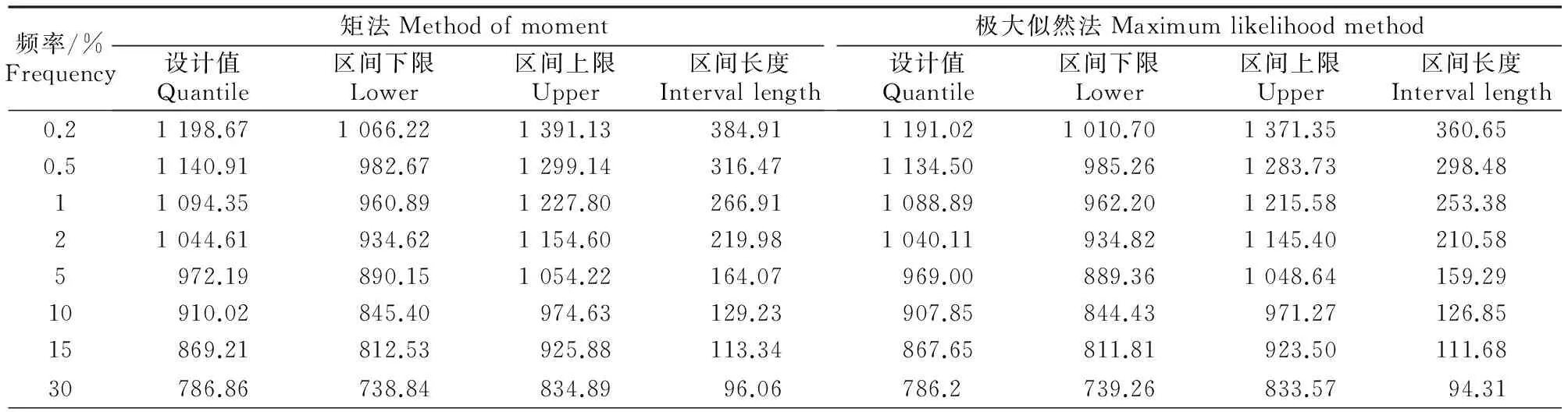
表 3　蓝田站不同设计频率下年降水量设计值及其在95%置信水平下的置信区间Table 3　Annual precipitation quantile estimation and its 95% confidence interval under different design frequencies in Lantian station　mm

表 3(续)　Continued table 3

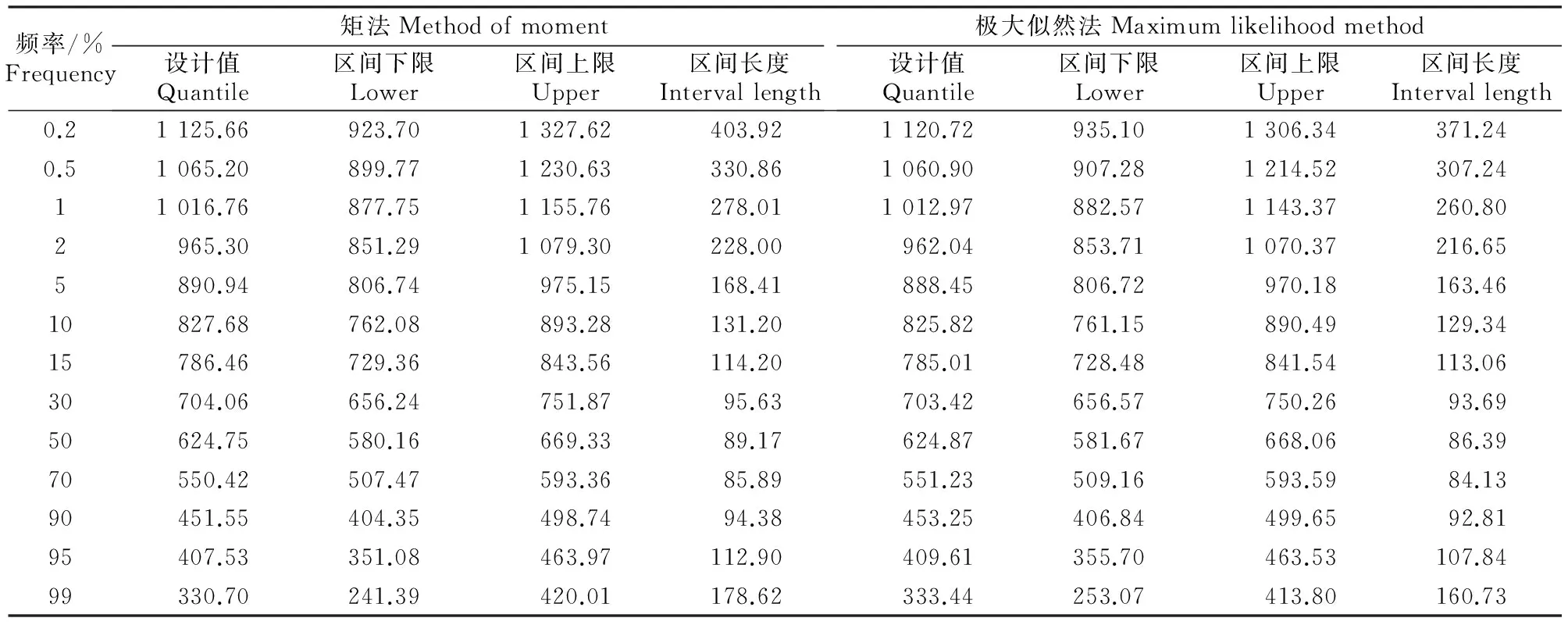
表 4　户县站不同设计频率下年降水量设计值及其在95%置信水平下的置信区间Table 4　Annual precipitation quantile estimation and its 95% confidence interval under different design frequencies in Huxian station　mm

为了反映出置信区间与经验点据之间以及频率曲线与经验点据之间的关系，表明置信区间能够用来度量水文设计值的不确定性，根据表1～4的计算结果，先点绘出不同测站的年降水量经验频率点据，然后绘制出各水文站理论频率曲线以及置信区间上下限曲线，结果见图1～4。

图 1　基于MOM和ML估算周至站不同设计频率下的年降水量设计值及其95%置信水平下的置信区间Fig.1　MOM and ML estimated annual precipitation quantile and its 95% confidence interval under different design frequencies for Zhouzhi station

由图1～4可以看出，频率曲线的中下部与经验点据拟合效果较好，而在曲线的两端，偏差较大。在频率曲线高尾部，各测站运用MOM和ML估算的水文设计值都比实测的降雨量小；在频率曲线低尾部，各测站运用MOM和ML估算的水文设计值都比实测的降雨量大。但是，各测站年降水量的经验频率点据基本上都被包含在设计值的区间上限和区间下限2条曲线之间，尽管有测站会出现一两个经验频率点据落在设计值的区间上限和下限所围成的曲线区间外，但距离也十分接近。说明置信区间可以为设计值的估算提供相应可靠的取值范围，从而降低水文设计值的不确定性。

图 2　基于MOM和ML估算临潼站不同设计频率下的年降水量设计值及其95%置信水平下的置信区间Fig.2　MOM and ML estimated annual precipitation quantile and its 95% confidence interval under different design frequencies for Lintong station

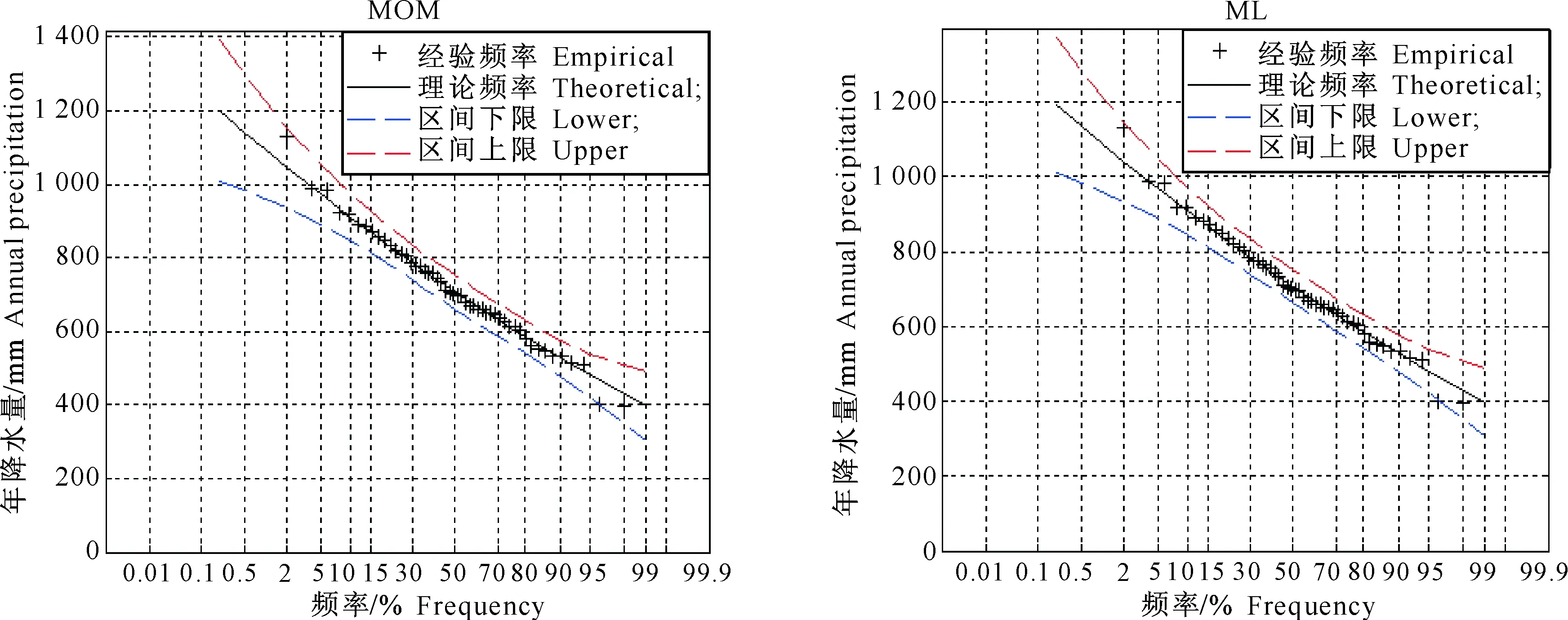
图 3　基于MOM和ML估算蓝田站不同设计频率下的年降水量设计值及其95%置信水平下的置信区间Fig.3　MOM and ML estimated annual precipitation quantile and its 95% confidence interval under different design frequencies for Lantian station

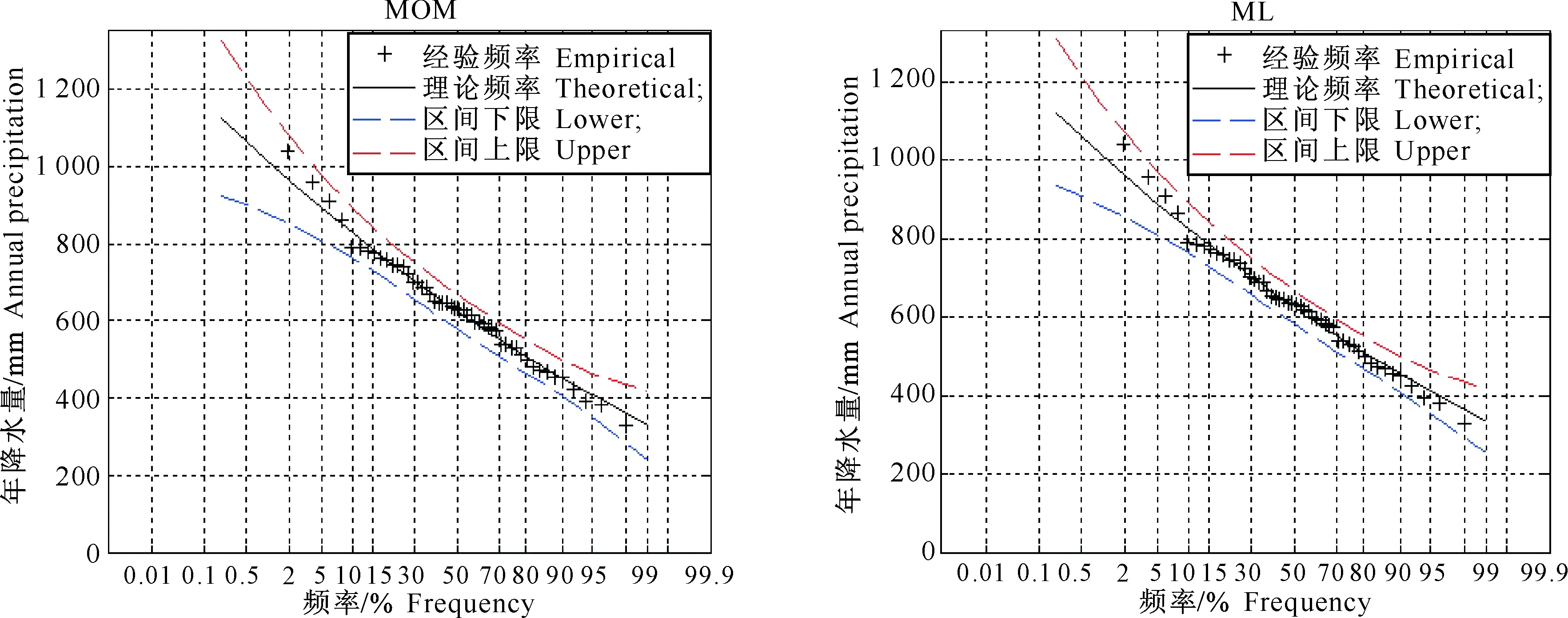
图 4　基于MOM和ML估算户县站不同设计频率下的年降水量设计值及其95%置信水平下的置信区间Fig.4　MOM and ML estimated annual precipitation quantile and its 95% confidence interval under different design frequencies for Huxian station

5　结　论

本文研究了基于矩法和极大似然法估算参数设计值置信区间的计算方法，通过对陕西省关中地区周至、临潼、蓝田和户县4个气象测站年降雨量序列进行实例计算，结果表明：置信区间能够用来描述水文设计值的不确定性，为水文设计值的估算提供相对可靠的变动范围，可提高设计值估算的精度。在相同设计频率下，无论是低频还是高频，极大似然法估算的置信区间长度均比矩法小，说明利用极大似然法估算设计值的置信区间能够更加有效地降低水文设计值的不确定性。因此，在实际工作中更加推荐使用极大似然法估算水文设计值的置信区间。另外，关于选用其他参数估算方法(如概率权重矩法、线性矩法等)计算设计值的置信区间仍需进一步研究。

[1]叶守泽，夏军.水文科学研究的世纪回眸与展望 [J].水科学进展，2002，13(1):93-104.

Ye S Z，Xia J.Century review and prospect of research on hydrological sciences [J].Advance in Water Science,2002,13(1):93-104.

[2]金光炎.水文频率计算成果的合理性分析 [J].水文，2009，29(2):10-14.

Jin G Y.Rationality analysis of results on hydrological frequency calculation [J].Journal of China Hydrology,2009,29(2):10-14.

[3]Tung Y K，Yen B C.Hydrosystems engineering uncertainty analysis [J].New York:McGraw-Hill Education,2005.

[4]Stedinger J R.Confidence intervals for design events [J].Journal of the Hydraulics Division,1983,109(1):13-27.

[5]Bobée B.Sample error of T-year events computed by fitting a Pearson type 3 distribution [J].Water Resources Research,1973,9(5):1264-1270.

[6]Hydrology Subcommittee.Cuidelines for determining flood flow frequency,Bulletin 17A [R].Washington D C:U.S.Water Resources Council,1977:102-108.

[7]Hydrology Subcommittee.Cuidelines for determining flood flow frequency,Bulletin 17B [R].Washington D C:U.S.Water Resources Council,1982:90-95.

[8]Condie R.The log Pearson type 3 distribution:the T-year event and its asymptotic standard error by maximum likelihood theory [J].Water Resources Research,1977,13(6):987-991.

[9]Kite G W.Confidence limits for design events [J].Water Resources Research,1975,11(1):48-53.

[10]Hardison C H.Confidence limits for flood-frequency curves computed from samples from Pearson type 3 populations [J].Journal of Research U.S.Geological Survey,1976,4(5):545-547.

[11]Cramer H.Mathematical methods of statistics [M].Princeton,New Jersey:Princeton University Press,1999.

[12]金光炎.水文统计原理与方法 [M].北京:中国工业出版社,1964:232-233.

Jin G Y.The principle and method of hydrologic statistics [M].Beijing:China Industry Press,1964:232-233.

[13]詹道江，徐向阳，陈元芳.工程水文学 [M].4版.北京:中国水利水电出版社,2010:142-143.

Zhan D J,Xu X Y,Chen Y F.Engineering hydrology [M].4 th Ed.Beijing:China Water Power Press,2010:142-143.

[14]Bobée B,Ashkar F.The gamma family and derived distributions applied in hydrology [M].Littleton,CO:Water Resources Publications,1991.

[15]余泱悦,贺信.P-Ⅲ曲线的极大似然估计及应用 [J].人民长江,2012,43(21):21-23.

Yu Y Y，He X.The maximum likelihood estimation and application of Pearson type 3 curve [J].Yangtze River,2012,43(21):21-23.

[16]黄振平.水文统计学 [M].南京:河海大学出版社，2003:112-121.

Huang Z P.Hydrologic statistics [M].Nanjing:Hohai University Press,2003:112-121.

Estimation of confidence interval for hydrologic design values

LIANG Jun，SONG Songbai

(CollegeofWaterResourcesandArchitecturalEngineering,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)

【Objective】 This paper studied estimation methods for hydrologic quantile confidence interval under given design standard and assessed the uncertainty of design value.【Method】 MOM and ML methods were used to study P-Ⅲ distribution hydrologic quantile confidence interval and figure out 95% confidence interval of hydrologic quantile estimation under different design frequencies at four meteorological stations in Guanzhong area.The results from MOM and ML were also compared and analyzed.【Result】 At the design frequency of 0.2%,confidence interval lengths of hydrologic quantile under 95% confidence level based on ML for the 4 hydrologic stations of Zhouzhi,Lintong,Lantian and Huxian were 414.28,338.88,360.65,and 371.24,while those based on ML were 546.61,435.64,384.91,and 403.92,respectively.At the design frequency of 99%,confidence interval lengths of hydrologic quantile under 95% confidence level based on ML for Zhouzhi,Lintong,Lantian and Huxian were 144.44,124.93,177.67,and 160.73,while those based on ML were 183.28,151.26,187.31,and 178.62,respectively.Independent of design frequency,confidence interval lengths of hydrologic quantile based on ML were always smaller than based on MOM.【Conclusion】 Confidence interval can provide relatively reliable range of variation for the hydrologic quantile estimation and the estimated confidence interval lengths based on ML were more effective in reducing the uncertainty of hydrologic quantile.

hydrologic quantile;design standard;standard error;confidence interval;Guanzhong area

时间:2016-09-0709:03DOI：10.13207/j.cnki.jnwafu.2016.10.031

2015-04-17

国家自然科学基金项目(51179160，50879070，50579065)；高等学校博士学科点专项科研基金项目(20110204110017)

梁骏(1990-)，女，湖南长沙人，在读硕士，主要从事流域水文模拟及水文预报研究。E-mail：460132683@qq.com

宋松柏(1965-)，男，陕西永寿人，教授，博士生导师，主要从事水文水资源研究。E-mail：ssb6533@nwsuaf.edu.cn

P333.6

A

1671-9387(2016)10-0221-08

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20160907.0903.062.html