基于Matlab的物理混沌实验仿真平台开发

张玉霞, 池水莲, 高亚妮, 林伟明

(1. 华南理工大学 物理与光电学院, 广东 广州　510640； 2. 华南理工大学 电力学院, 广东 广州　510640)



基于Matlab的物理混沌实验仿真平台开发

张玉霞1, 池水莲1, 高亚妮1, 林伟明2

(1. 华南理工大学 物理与光电学院, 广东 广州510640； 2. 华南理工大学 电力学院, 广东 广州510640)

利用Matlab GUI建立了混沌系统实验仿真平台,可以在该平台界面输入和改变参数,分析各参数对实验结果的影响,也可以自己设计和改变混沌系统,进行深度学习和探索。利用该平台可以得到多维混沌吸引子的分解图像和数据,直观地观察投影图和时域图、Lyapunov指数、功率谱、分维数等混沌指标。用仿真平台研究非线性电路中的混沌现象,能准确地观察到混沌吸引子的行为特征,结果与理论分析十分吻合。

物理混沌实验； Matlab； 图形用户界面； 仿真平台

混沌是连接确定性运动和随机性运动的纽带,被视为20世纪继相对论和量子力学后的第三重大发现。混沌运动的发现使人们重新审视许多已被定论的研究成果,而且澄清了许多重大现象的实际产生原因,并实现了许多常规定律无法实现的工作特性。由于混沌运动理论性强,对数学基础要求高,概念和规律抽象,教学效果总是不尽如人意[1-3]。近年来,不少学校改进了混沌运动实验条件,取得了一定效果,但由于实验设计复杂,特别是非线性组件采用的集成式设计,学生无法观察元件的运作过程,实验效果仍然有待提高。计算机虚拟仿真实验具有良好的可控性、重复性、易观察和经济性等优点,有望为科研和教学工作提供新的辅助手段[4-7]。

本文利用Matlab GUI开发了一套物理混沌实验仿真平台,实现了lorenz系统、chen系统、lü系统、rössler系统等多个混沌系统实验的计算机仿真[8-10],不但减少了实验前期投资,而且清晰、准确地再现了蔡氏(Chua)电路、Colpitts振荡电路等各种混沌电路实验现象,了解各参量的动态演化过程。

1　仿真平台总体设计

为了提供平台的可扩展性,本物理混沌实验仿真平台采用模块化设计,即将每个具体实验作为一个子模块,以便于系统维护和增加新的实验项目。该平台主要包括混沌系统、混沌实验和探索实验3部分。

混沌系统分为一维混沌、二维混沌、三维混沌、四维混沌和其他混沌5部分,每部分又包含若干个子模块。

混沌实验分为Chua混沌实验、Colpitts振荡器电路实验、开关功率转换器实验、忆阻混沌电路实验和其他混沌实验等5部分。利用Matlab对混沌进行仿真,过程简单,可以设计出丰富、直观的界面且操作方便。可以在界面上直接输入和改变参数,直观地分析各参数的变化对实验结果的影响。

探索性实验部分给出部分源程序,包括Poincare映射轨迹、分岔图、Lyapunov指数和其他指标,方便学生在基本程序基础上进行进一步拓展学习和研究。

物理混沌实验仿真平台软件可以脱离Matlab环境独立运行,有利于软件的维护和稳定。

2　仿真混沌系统设计实例

以三维混沌实验为例,介绍物理混沌实验仿真平台的开发过程。通过分析lorenz系统、chen系统、lü系统、rössler系统、liu系统、qi系统的数学模型,可以看出:三维连续自治混沌系统的数学模型拥有相似的基本结构,都是由3个变量x、y、z组成。

(1)

但是,并不是所有通式方程(所有参数)所对应的系统都是混沌。通过数值仿真和反复调整系统参数,可以构造多种三维连续自治混沌系统。

这里列出lorenz系统、chen系统、lü系统和rössler系统的典型的三维混沌动力学系统,分别描述为：

lorenz系统:

chen系统:

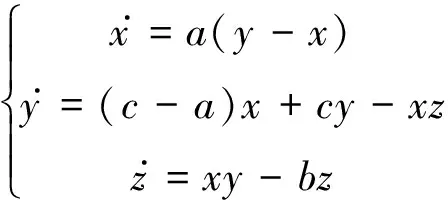
lü系统：

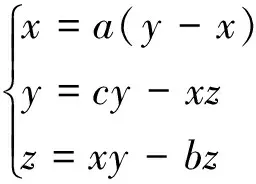
rössler系统：

其中a、b、c为实参数。当取相应的值时,系统处于混沌状态。它们的典型混沌吸引子如图1所示。

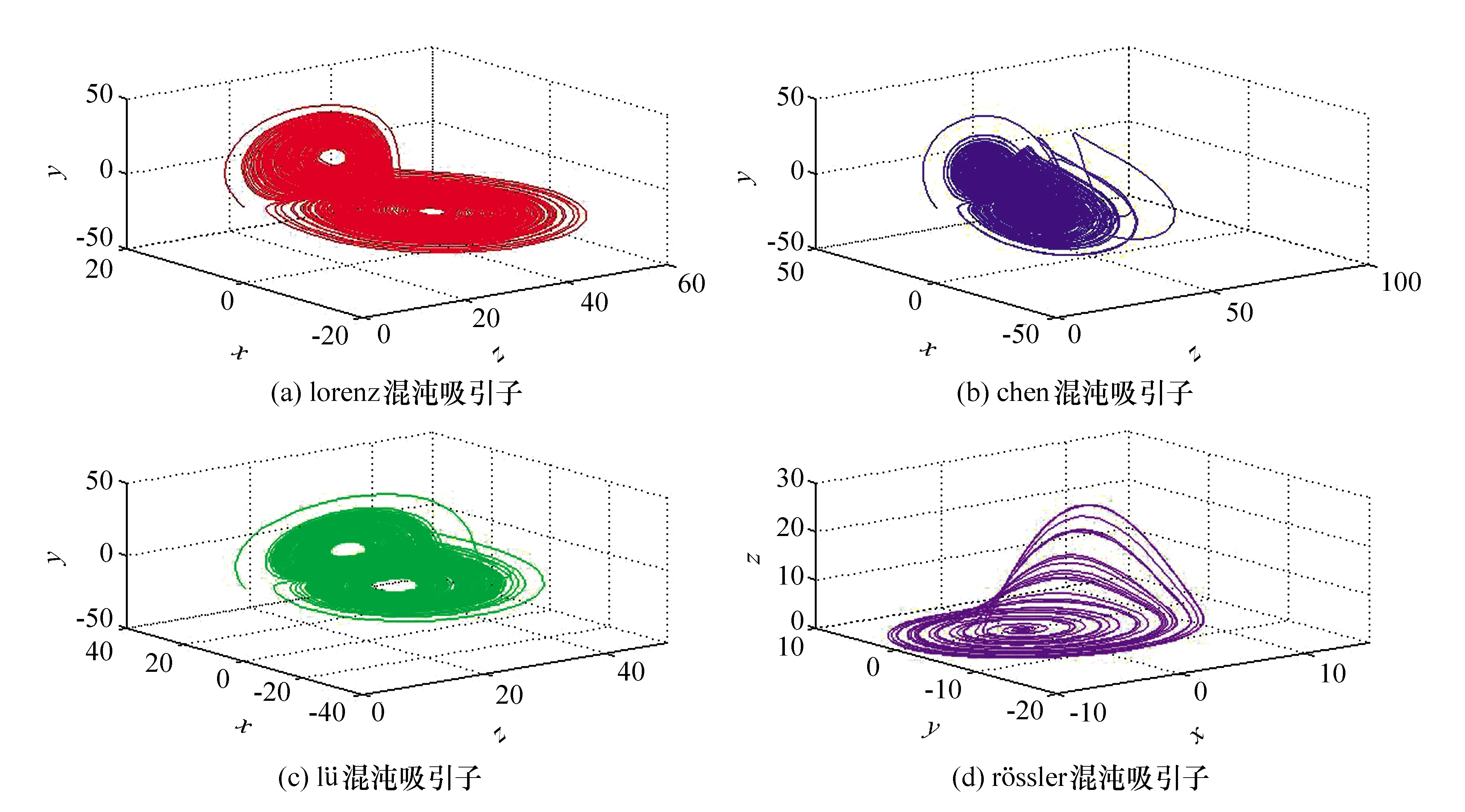
图1　4个混沌系统的典型吸引子

通过仿真平台,不仅可以看到三维混沌的整体形态,而且可以独立地看到xy、yz或xz中任意二维混沌形态和x、y或z的一维时域图像。图2和图3分别是lorenz系统的在二维和一维上的投影图。利用三维、二维和一维各方位图像加深对混沌细节的理解,理解混沌产生的原因,弥补真实实验只能用示波器观看二维图像的缺憾。

3　仿真混沌实验设计实例

蔡氏(Chua)电路是经典的混沌电路,下面以蔡氏电路为例分析仿真平台的内部设计。

图4所示的蔡氏电路是一个三维自治系统,它由4个线性元件(电感L,电阻R,电容C1,C2)和1个非线性电阻Nr组成。蔡氏电路的方程组为

图2　lorenz系统混沌吸引子平面投影

图3　lorenz系统的时域波形

图4　Chua混沌电路

(2)

式中V1、V2和i3分别是电容C1、C2两端的电压和流过电感L的电流,f(V1)是描绘电阻Nr的i-V特性折线(见图5)的多项式,为

图5　非线性电阻的伏安特性曲线

式中Ga、Gb分别表示内外折线的斜率,E为转折点电压。

当R=1.7 kΩ,L=20 mH,C1=10 nF,C2=100 nF,Ga=-0.76 ms,Gb=-0.5 ms时,蔡氏电路的典型双涡旋混沌吸引子如图6所示,相应的二维和一维投影和时域波形如图7和图8所示。

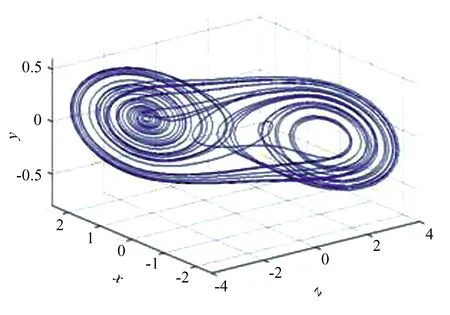
图6　Chua系统混沌吸引子

图7　Chua系统混沌吸引子平面投影

图8　Chua系统的时域波形

对比方程组(1)和(2),方程组(1)是无量纲的数学模型,方程组(2)是有物理内涵的充放电耗散电路表达式,数学模型中的参量对应物理电路中的电容、电压以及电容、电流。仿真平台要完成从数学模型到物理仿真实验的转化,因此在每一个具体实验中要加入实验目的、实验原理、实验模型和实验电路等信息,特别是在实验原理中要详细说明在混沌电路中,把无量纲的数学模型如何转化为混沌电路方程的过程。仿真平台建立了真实的混沌电路和数学模型的转化关系。通过Matlab再现实验现象,得到从宏观到微观、从三维到一维的每个时间和坐标点上的详尽信息。该仿真平台提高了实验效果,有助于加深学生对混沌理论的理解。

4　探索实验

仿真平台提供了进一步研究混沌系统和混沌电路的平台。把部分经典源程序开放出来,方便研究混沌系统的其他特征,例如系统的耗散特性、不稳定平衡点、运动轨迹的有界性；方便进行诸如分岔图、Lyapunov指数、功率谱、分维数等相关参数的研究；也可方便地寻找新的混沌系统、设计新的混沌实验[11-12]。

5　结语

用Matlab GUI设计混沌实验仿真平台方法简单,不但可以根据需要设计出丰富的实验界面,而且可直接在界面中输入和改变参数而不需要改变源程序,保证平台的友好和稳定性。利用该平台有利于分析不同参数条件下的实验结果,有利于全面了解不同时间和空间的详细信息,把抽象的混沌问题进行简明、直观的动态展示,为混沌理论和实验教学提供了方便,为相关教学研究提供了新途径。

References)

[1] 包伯成.混沌电路导论[M].北京:科学出版社,2013.

[2] 於黄忠.近代物理实验[M].广州:华南理工大学出版社,2013.

[3] 叶昕,张茂青,周纯.蔡氏电路的仿真研究[J].电工电气,2009(4):48-51.

[4] 王玮,刘亦萍.基于MATLAB的蔡氏混沌非线性电路的仿真研究[J].科技视界,2013(33):67-68.

[5] 王晓辉,谢胜曙,张志伟.基于Matlab的混沌系统仿真与分析[J].现代电子技术,2006,29(10):105-107.[6] 蒋国平,程艳云.蔡氏混沌非线性电路及其频率特性研究[J].电气电子教学学报,2002,24(5):5-7.

[7] 刘洪臣,孙立山.混沌电路的创新综合性实验的设计与实现[J].电气电子教学学报,2011,33(3):70-73.

[8] 林若波.混沌电路系统的模型仿真与电路实现[J].电路与系统学报,2009,14(3):121-125.

[9] 林志勇,丁群,孙圣和.混沌序列生成系统的仿真设计及其应用[C]//2008中国仪器仪表与测控技术进展大会论文集.2008:279-282.

[10] 王永生,肖子才,孙瑾,等.Duffing混沌系统电路仿真研究[J].电路与系统学报,2008,13(1):132-135.

[11] 雷腾飞,陈恒,王震.Shim izu-Morioka混沌系统的电路设计及自适应控制研究[J].温州大学学报:自然科学版,2015,36(1):23-31.

[12] 李国辉,李亚安,杨宏.混沌吸引子的DSP Builder设计方法[J].探测与控制学报,2009,31(6):60-63.

Development of chaos-physics experiments simulation platform based on Matlab

Zhang Yuxia1, Chi Shuilian1, Gao Yani1, Lin Weiming2

(1. School of Physics and Photoelectricity,South China University of Technology,Guangzhou 510640,China;2. School of Electric Power,South China University of Technology,Guangzhou 510640,China)

By using Matlab GUI,a set of chaotic system and experimental simulation platform is established. The users can enter and change the parameters in the interface,intuitive analysis of the impact of each parameter on the experimental results. The chaotic system for deep learning and exploration can also be designed and changed. Platform of chaotic system and simulation experiment can obtain multidimensional chaotic attractor of the decomposition of image and data,it is convenient to directly observe the time domain and projection map, and can calculate the Lyapunov exponent and power spectrum,dimension chaotic indexes. The chaotic phenomena in nonlinear circuit are studied from two angles of theoretical system and experimental simulation. The simulation experiment and theory are very consistent,which can accurately observe the behavior characteristics of the chaotic attractor.

chaos-physics experiments； Matlab； graphie user interface； simulation platform

10.16791/j.cnki.sjg.2016.10.030

2016-04-28

国家自然科学基金项目(61503140)；全国教育信息技术研究“十二五”规划项目(136241506)；华南理工大学教研教改项目(Y1150870)；华南理工大学探索性实验项目(Y1150410)；华南理工大学学生研究计划项目(Y9160280)

张玉霞(1976—),女,湖北襄阳,博士,讲师,主要研究方向为复杂系统的建模和应用.E-mail：zhangyux@scut.edu.cn

O415.5

A

1002-4956(2016)10-0119-04