双闭环控制的三电平逆变电路Simulink仿真实验

李文娟, 王　超, 冯　杰, 周美兰, 高晗璎

(哈尔滨理工大学 电气与电子工程学院, 黑龙江 哈尔滨　150080)



双闭环控制的三电平逆变电路Simulink仿真实验

李文娟, 王超, 冯杰, 周美兰, 高晗璎

(哈尔滨理工大学 电气与电子工程学院, 黑龙江 哈尔滨150080)

针对开环的三电平逆变电路稳定性差、动态响应慢、带载能力弱等问题,提出了电压、电流双闭环的控制方案。选取二极管箝位式三电平逆变电路作为被控对象,建立其在同步旋转坐标系下的数学模型,分别对电流环和电压环进行设计。电流环包括基于d、q轴的电感电流前馈解耦及PI参数的设计;电压环包括基于d、q轴的电容电压前馈解耦及控制器参数的设计。在Simulink仿真实验平台上,建立了双闭环控制的三电平逆变电路的仿真模型,分析了突变负载情况下双闭环控制的逆变输出电压和电流的仿真波形。

逆变电路； 仿真实验； 三电平； 双闭环控制

电力电子技术是电气工程及其自动化专业不可或缺的一门专业基础课,在培养专业人才中占有重要地位。在电力电子电路中,逆变电路的应用非常广泛,交流电动机调速用的变频器、不间断电源、感应加热电源的核心部分都是逆变电路。因此,逆变电路在教学中具有举足轻重的地位[1]。

在目前逆变电路的教学中,主要讲授半桥逆变电路、单相全桥逆变电路和三相桥式逆变电路[2]。但是,这些电路结构无法满足高压、大功率场合的需求,因此,三电平逆变技术得到迅猛发展。为了使学生的知识与现代前沿技术接轨,将三电平逆变电路应用于教学势在必行。此外,由于闭环控制系统精度高,输出电压电流稳定性好、动态响应能力强、受系统参数变化影响小,因此成为逆变电路发展的重要方向。

本文选取二极管箝位式三电平逆变电路作为研究对象,首先建立了三电平逆变电路在dq坐标系的数学模型,进而采用电流内环、电压外环的双闭环控制,研究在不同负载突变下逆变电路的输出波形,从而验证所设计的三电平逆变电路的稳定性和响应能力。在Matlab/Simulink中搭建仿真模型,借助于仿真波形,帮助学生掌握三电平逆变电路的工作原理和闭环控制思想,并使理论教学与实际应用接轨[3]。

1　三电平逆变电路

1.1三电平逆变电路拓扑结构

二极管箝位式三电平逆变电路是由直流电源E、两个直流分压电容C1和C2、三相三电平逆变桥、三相LC滤波器及三相负载组成。其中三相滤波电感值均为L,电感损耗等效为r,三相滤波电容大小为C。三电平逆变电路的原理图如图1所示[4],其中,ia、ib、ic分别为三相电感电流,ioa、iob、ioc分别为三相负载电流,ua、ub、uc为三相电容电压。

图1　三电平逆变电路的原理图

相比于普通三相桥式逆变电路,三电平逆变电路具有谐波含量少、电压应力小、开关损耗低等特点,适用于高压、大功率场合。

1.2三电平逆变电路数学模型

用三态开关变量Sa、Sb、Sc分别表示各桥臂的三种开关状态,分别对应着-1、0、1三种状态[5],则三相输出的相电压可以用开关变量和直流输入电源表示为：

把负载电流作为扰动输入,取电感电流、电容电压作为状态量,电流及电压方向如图1所示。根据KCL及KVL可以列出电路的微分方程[6],经过一系列推导可以得到abc三相静止坐标系下的三电平逆变电路的数学模型为

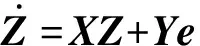
其中,

三相静止abc坐标系到两相旋转dq坐标系的变换矩阵为:

通过坐标变换,可以得到dq同步旋转坐标系下的三电平逆变电路数学模型[7],见式(1)和式(2)。

(1)

(2)

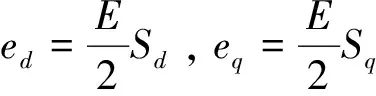
2　三电平逆变电路双闭环控制系统设计

图2　三电平逆变电路双环控制系统框图

2.1 电流环设计

根据式(1)可知,d、q轴电流存在耦合,因此不能用简单的负反馈控制。为了降低控制器设计的难度,需要对d、q轴电流进行前馈解耦[11],然后再进行PI调节,解耦方程为

(3)

根据式(3)设计了图3所示的电流环解耦控制图,引入电流反馈和电压前馈后,可以有效地消除耦合及电压影响。

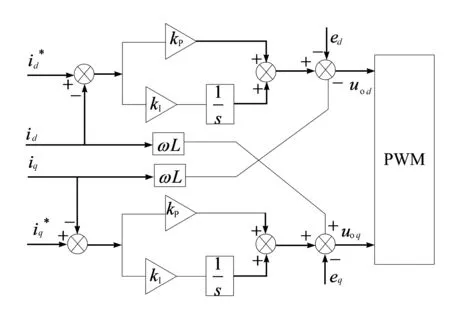
图3　电流环解耦控制图

由于d、q轴电流具有对称性,因此PI控制器的参数可以取定相同值,现只需对d轴电流分量进行分析。图4为d轴电流闭环控制结构图,其中KPWM为三电平逆变桥的等效增益,Ts为电流环采样周期。

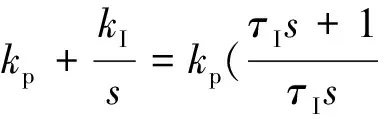
可得到d轴电流闭环的闭环传递函数为

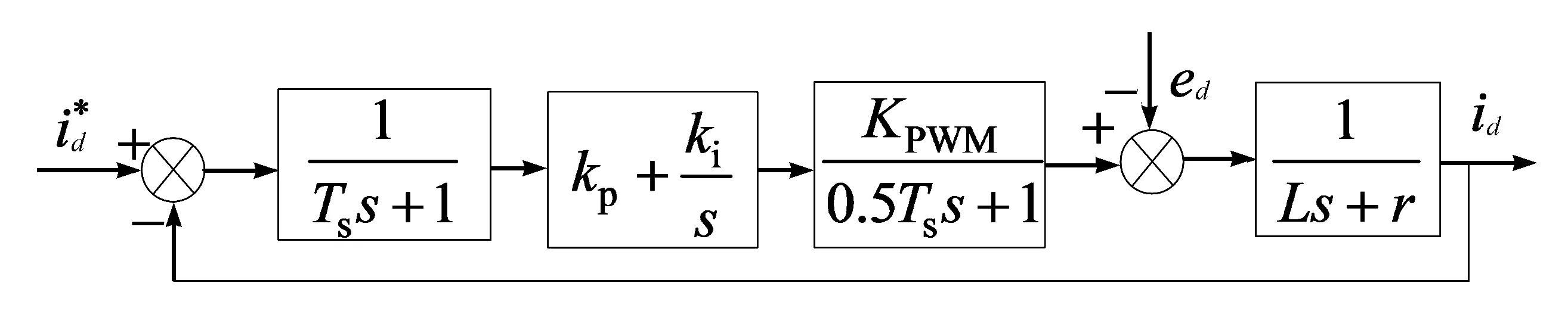
图4　d轴电流闭环控制结构图

图5　d轴电流闭环控制简化图

按照典型的I型系统设计,参数ξ取0.707时,系统性能最好。为了抵消电流控制传递函数的极点,取τI=L/r。因此根据系统实际需要,将具体参数代入,即可得到kP、kI,则kP=10、kI=50。

2.2电压环设计

由式(2)可知,电压也存在着耦合,因此也需要解耦。电压环设计与电流环相似,电压控制系统解耦方程为:

电压环解耦控制如图6所示,经过解耦及PI调节后,实现d、q轴电压的独立控制。

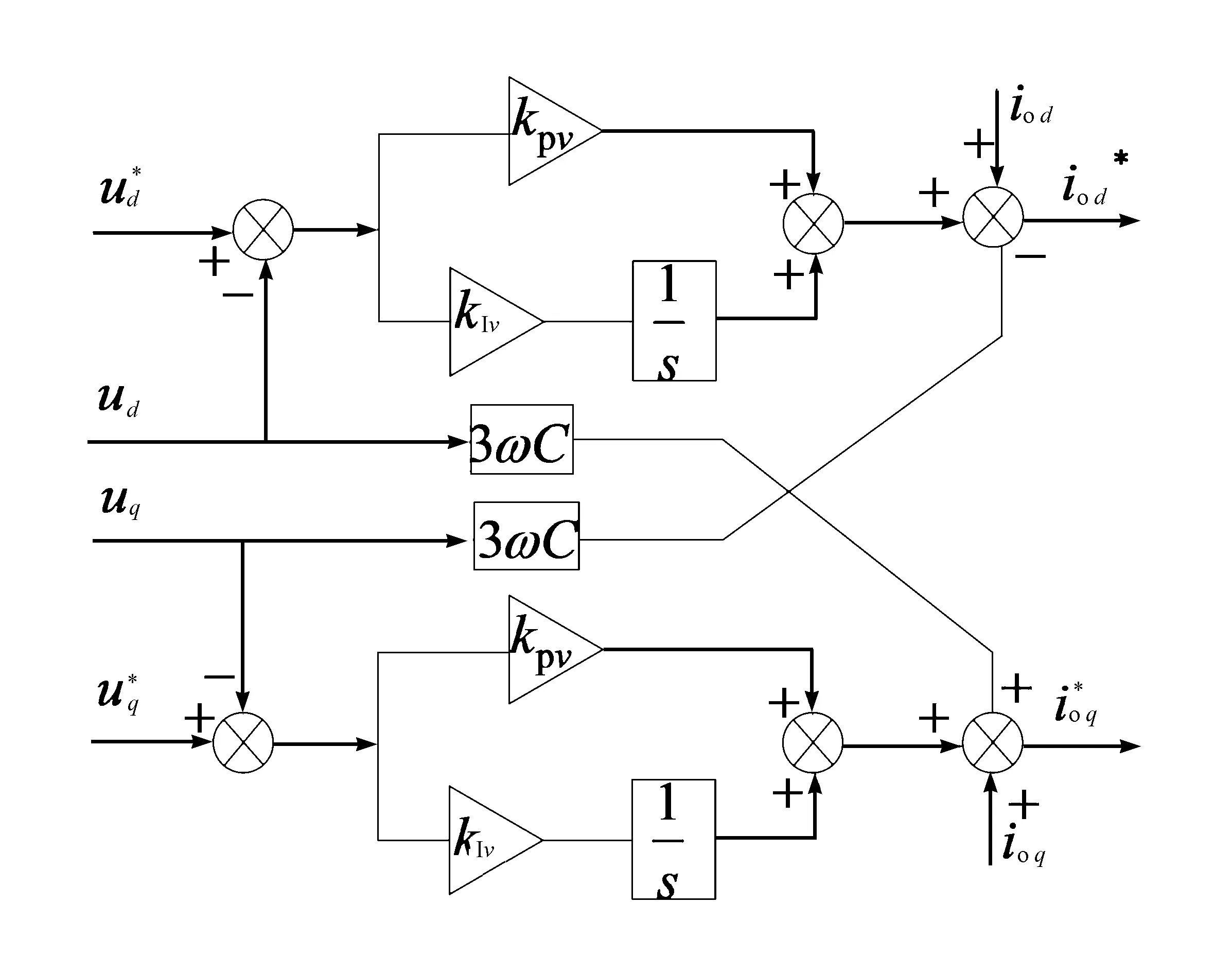
图6　电压环解耦控制图

d、q轴电压分量同样具有对称性。以d轴电压为例,得出d轴电压环控制的结构图(见图7),其中包括电压采样延迟环节、PI控制环节、电流环的传递函数[13]。为了分析方便,忽略负载电流io d的扰动,并将电流环近似等效为一阶惯性环节,从而与电压采样的延迟环节合并。合并后的小时间常数用Tp表示,Tv为PI调节器参数,得到简化的d轴电压闭环控制结构图,如图8所示。

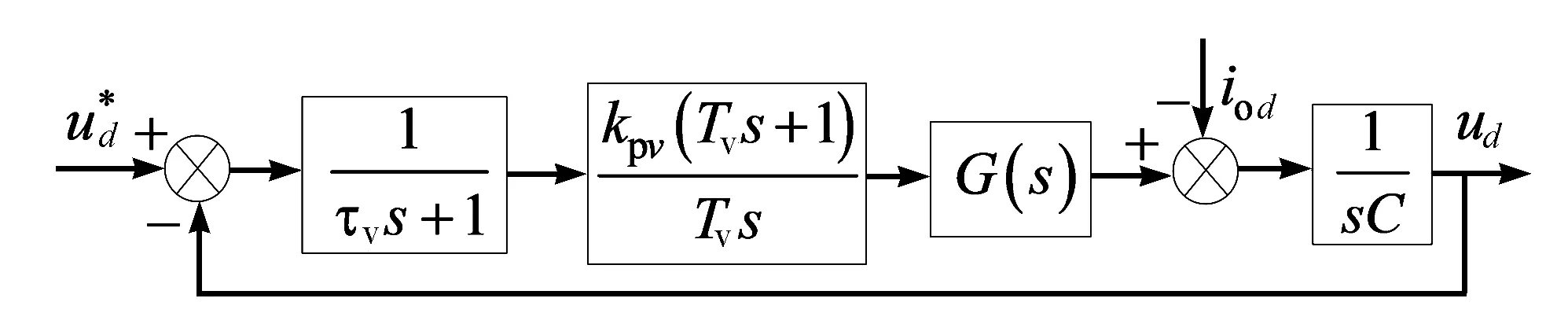
图7　d轴电压闭环控制的结构图

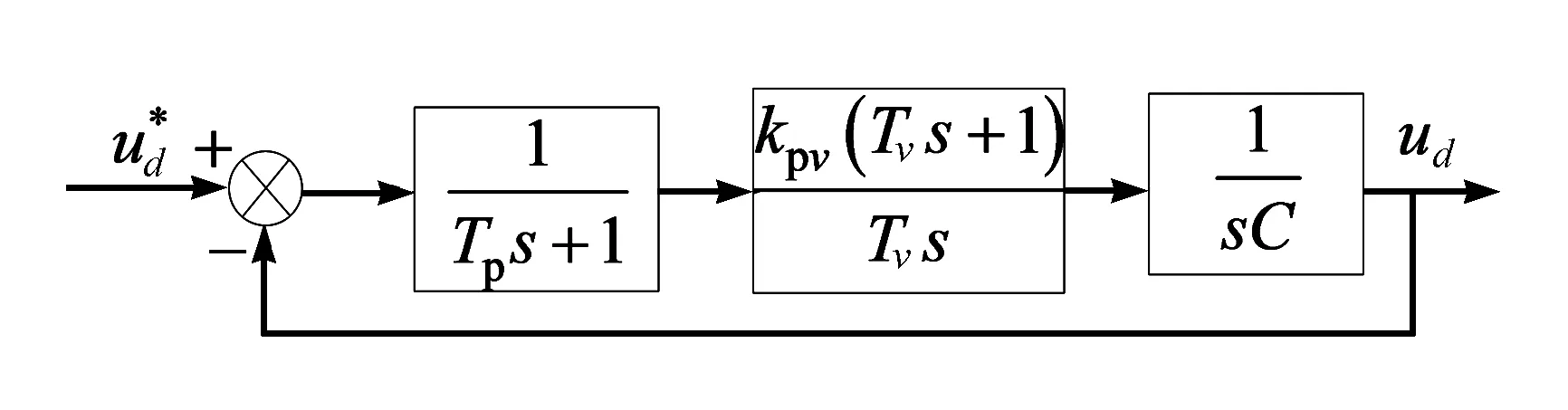
图8　d轴电压闭环控制的简化结构图

可以求出d轴电压闭环的开环传递函数为

电压闭环主要以抗干扰能力为目标,因此采用典型的II型系统进行设计。电压中频宽h=Tv/Tp,一般取h=5,又由II型系统参数关系可得:

根据本文具体参数,经计算,最终电压环的PI控制器选取kPv=1,kIv=100。

3　仿真及结果分析

3.1仿真模型的建立

在Simulink中建立三相三电平逆变电路的仿真模型(见图9),主要包括三电平逆变电路拓扑模块、三相LC滤波器模块、三相交流负载模块、abc/dq变换及反变换模块、双闭环的控制模块以及PWM发生器模块。其中,abc/dq变换模块包括三相电感电流、三相电容电压、三相负载电流的坐标变换,共3个坐标变换,进而得到dq坐标系的直流分量,便于PI调节,实现无静差跟踪。双闭环控制模块包括电流内环和电压外环控制,分别对一种负载状态突变为另一种负载状态进行仿真。在仿真模型中选取表1所示仿真参数。

表1 三电平逆变电路仿真参数

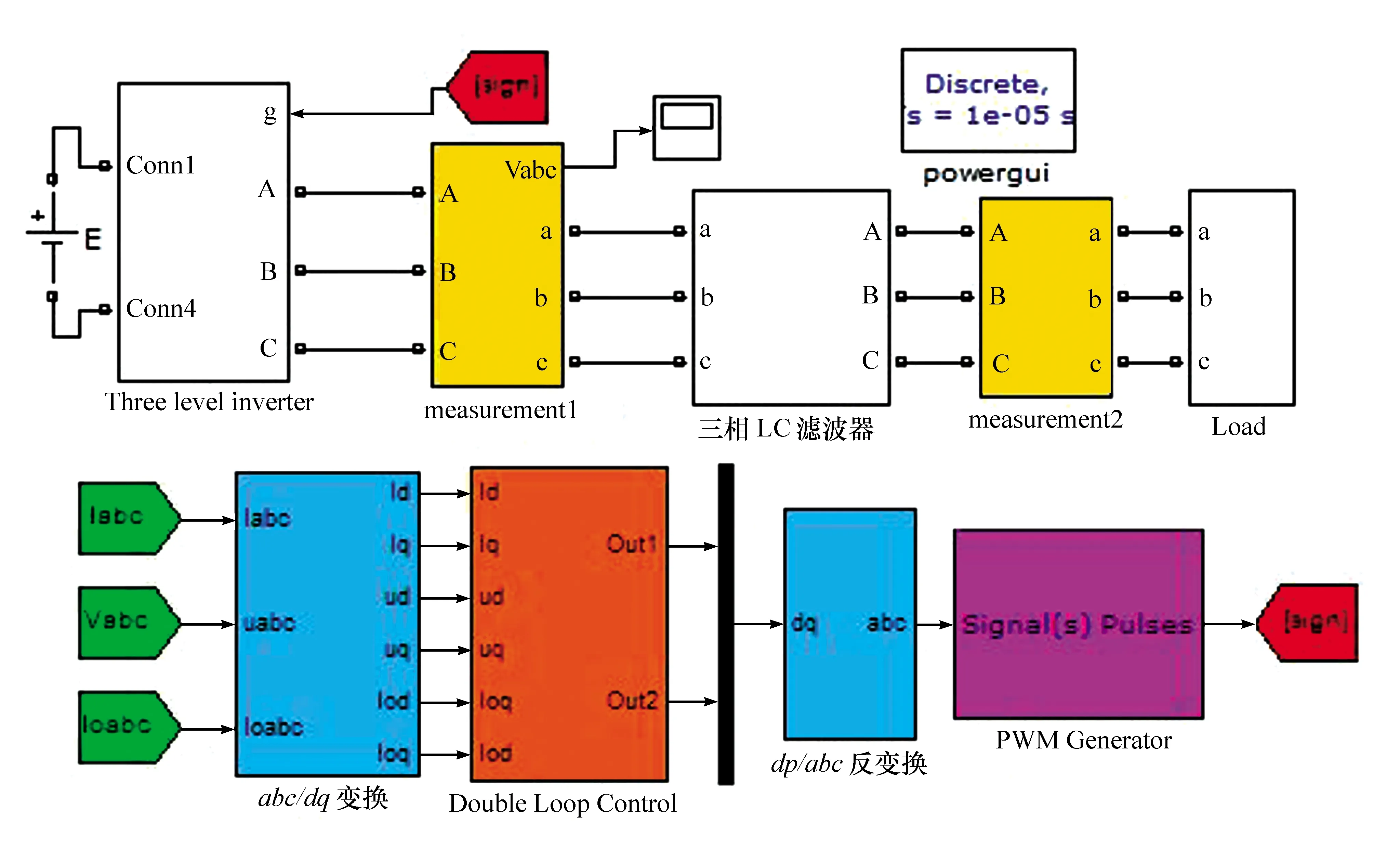
图9　三相三电平逆变电路双闭环控制系统仿真模型

3.2仿真结果分析

为了验证基于dq轴解耦的双闭环控制方法的正确性,首先将纯阻性负载由20 Ω在0.06 s时突变为40 Ω,输出三相电压波形如图10(a)所示。在0.06 s时突变后,b相电压正峰值明显增大,c相电压负峰值有所提升,但是接近0.07 s时,三相快速达到稳定的状态。输出的三相负载电流波形如图10(b)所示,虽然突变时刻明显波动较大,但能够快速恢复稳定。同时给出线电压输出波形如图10(c)所示,线电压为五电平,符合三电平逆变电路的特点。

图10　在0.06 s时刻负载突变的电压及电流波形

为了更好地验证所设计的双闭环控制系统的正确性,在0.04 s时将负载由100 Ω的纯阻性负载突变为0.01 H的感性负载,在0.08 s时再突变为0.001 F的容性负载,输出电压及电流波形如图11所示。

图11　在0.04 s和0.08 s负载突变的电压及电流波形

由图11可见,在0.04 s及0.08 s的负载突变时刻,电压幅值有略微变化,整体波动不明显,电流波形不到半个工频即可快速稳定。仿真波形进一步证明了基于dq轴解耦的双闭环控制系统具有快速动态响应能力和良好的稳定性。

4　结语

三电平逆变电路采用电压电流双闭环控制方案具有更好的抗负载扰动能力。通过仿真波形可以直观地看出:三相三电平逆变电路在双闭环控制方案下,输出电压和电流波形效果非常好,动态响应速度快、抗负载干扰能力强,验证了控制方案的正确性。将Simulink仿真融入三电平逆变电路实验教学中,不仅可以使学生对逆变电路的原理有了深入的理解,还增强了学生的仿真实验能力。这种理论与实践相结合的教学模式能有效提高教学质量。

References)

[1] 李文娟,刘铜振,张经纬,等.单闭环单相PWM逆变系统的Saber仿真实验[J].实验技术与管理,2015,32(8):109-111.

[2] 林磊,邹云屏,钟和清,等.二极管箝位型三电平逆变器控制系统研究[J].中国电机工程学报,2005,25(15):35-37.

[3] 李文娟,程静思,黄怀翀,等.Simplorer在电力电子电路仿真实验中的应用[J].实验技术与管理,2014,31(11):111-113,120.

[4] 金红元,邹云屏,林磊,等.三电平PWM整流器双环控制技术及中点电压平衡控制技术的研究[J].中国电机工程学报,2006,26(20):66-67.

[5] 茆美琴,喻莉,徐斌,等.单相电流型逆变器的d-q控制及仿真研究[J].系统仿真学报,2011,23(12):2727-2731.

[6] 林涛,王彦章.双闭环逆变器控制策略仿真研究[J].电子科技,2014,27(7):120-123.

[7] 鲍陈磊,阮新波,王学华,等.基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J].中国电机工程学报,2012,32(25):133-142.

[8] Prabhakaran K K,Shyam K S,Manoj K N.Three level diode clamped inverter for field oriented control of induction motor[C]//Information and Communication(ICCPEIC).2013:115-118.

[9] 李鑫,姚勇涛,张逸成,等.采用电容电流内环的逆变器双闭环控制研究[J].电气传动,2008,38(2):23-25.

[10] 谢芬,鲁杰,潘丽.基于Simulink库仿真的单相逆变电源调节器设计[J].电子设计工程,2012,20(10):22-25.

[11] 雷亚雄,李建文,李永刚.基于准PR调节器电流双闭环LCL三相并网逆变器控制[J].电力系统保护与控制,2014,42(12):45-49.

[12] 文小琴,毕淑娥,游林儒.基于Matlab的电力电子技术仿真平台设计[J].电气电子教学学报,2014,36(4):105-106,110.

[13] 张珍珍,许春雨.三电平NPC型逆变器中点电位稳压器的设计[J].电气传动,2014,44(12):26-29.

Simulink simulation experiment of three-level inverter circuit with double closed-loop control

Li Wenjuan,Wang Chao,Feng Jie, Zhou Meilan, Gao Hanying

(College of Electrical and Electronic Engineering,Harbin University of Science and Technology,Harbin 150080,China)

Aiming at the problems of open-loop three-level inverter circuit poor stability,slow dynamic response,weak carrying capacity, the voltage-current double closed-loop control scheme is proposed. The diode-clamped three-level inverter circuit is regarded as the controlled object. The math model of inverter circuit on two-phase synchronous rotating coordinates is established. The designs of current loop and voltage loop are carried out respectively. The current loop includes the inductance current feed-forward decoupling based ondqaxis and the design of corresponding PI parameters. Voltage loop includes the capacitance voltage feed-forward decoupling based ondqaxis and the design of controller parameters. The simulation model of three-level inverter circuit with double closed-loop control is built in the Simulink simulation platform. The waveforms of the output voltage and current of the double closed-loop control under the condition mutation loads are analyzed.

inverter circuit; simulation experiment； three-level; double closed-loop control

10.16791/j.cnki.sjg.2016.10.028

虚拟仿真技术探索与实践

2016-04-20

黑龙江省学位与研究生教育教学改革资助项目(JGXM_HLJ_2015060)

李文娟(1968—),女,黑龙江哈尔滨,博士,教授,主要研究方向为电力电子装置与系统、成像质量评价.

TM464

A

1002-4956(2016)10-0110-05