用特殊性巧解定点定角定值问题

魏正清

(甘肃省临泽一中，734200)



用特殊性巧解定点定角定值问题

魏正清

(甘肃省临泽一中，734200)

解析几何中的定点、定角、定值问题,是高考考查的核心题型之一,是多年高考经久不衰的热点.这类问题常常以直线与圆锥曲线的位置关系为载体，以参数处理为核心需要，综合运用函数、方程、不等式、平面向量等诸多数学知识以及数形结合、分类讨论等多种数学思想方法求解.一般来说解法都比较单一,虽然有通法可循,但运算量大且过程繁琐是它最明显的特征.如何化繁为简,减少运算量、有效突破这一人人都颇感棘手的问题,是值得研究的课题,也是追求数学简洁美的根本要求.本文另辟蹊径,从特殊情形入手,先猜后证,给出处理解析几何中定点、定角、定值问题的简化策略.

一、定点问题

(1)求椭圆C的方程;

分析对第(2)问，如图1,探索以AB为直径的圆是否恒过平面内一定点,通常都是先求出以AB为直径的圆方程,再利用圆系的有关知识寻求定点,这样做难度过大,不易得手.如果从特殊情形入手,由特殊的圆,寻求特殊的点,然后先猜后证,就能化难为易,将问题迎刃而解.

(2)假设存在定点T(x0,y0)满足题意,设A(x1,y1),B(x2,y2).

当直线m的斜率不存在时,直线m的方程为x=0,易知A(0,1),B(0,-1)且以AB为直径的圆C1的方程是x2+y2=1.

将圆C1与圆C2的方程联立可得交点T(0,1).

以下只需验证当直线m的斜率存在时,也符合题意.

(

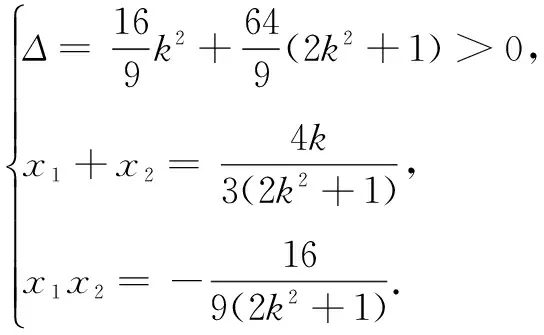
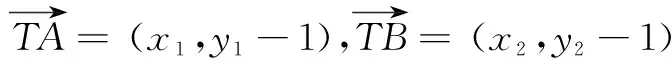
即当直线m的斜率存在时,以AB为直径的圆也过定点T(0,1).

综上所述,存在定点T(0,1)满足题意.

二、定角问题

(1)求抛物线C的方程;

(2)若点E在抛物线C上,且纵坐标为2,经过点(2,0)的直线l与抛物线C交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N,O为原点,求证:∠MON为定值.

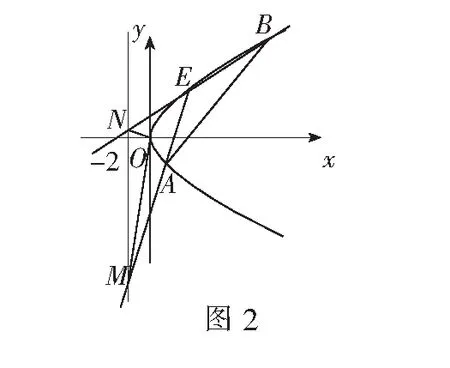
分析如图2,证明∠MON为定值,通常是验证tan∠MON的值为定值,这就需要将tan∠MON的求解转化为直线的倾斜角,进而转化为直线的斜率问题解决.这样处理既要寻求∠MON与某两条直线的倾斜角的关系,还要利用两角和与差的正切公式,问题方能得以解决,过程繁且运算量很大.如果能从特殊情形入手,取特殊点及特殊直线,先猜出∠MON的值,再进行验证,则有意想不到的收获.

解(1)y2=2x(过程略).

(2)易知点E(2,2),设直线l:y=k(x-2).设直线l与抛物线C交于A(x1,y1),B(x2,y2)两点.

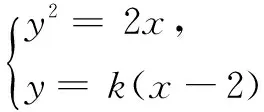
EB方程为y-2=2(x-2),令x=-2，得N(-2,-6).

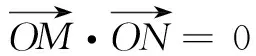
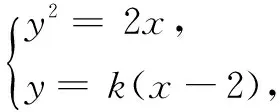
ky2-2y-4k=0，

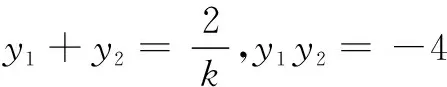
三、定值问题

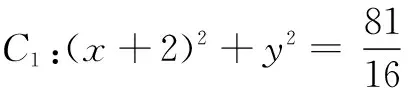
(1)求曲线C的方程.

(2)设点M(m,0),点Q为曲线C上位于x轴上方的动点.

(i)若m<0,写出直线MQ的倾斜角的取值范围;

(ii)证明:存在正数λ,负数m,使得

∠QC2M=λ∠QMC2.

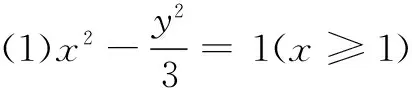
(ii)探索正数λ,负数m,使得∠QC2M=λ∠QMC2成立,按照正常思维实在难以着手；但若从极端情形入手,先猜出正数λ与负数m的值,再进行验证,定会柳暗花明.

设Q(x0,y0)(x0≥1,y0>0),如图3.

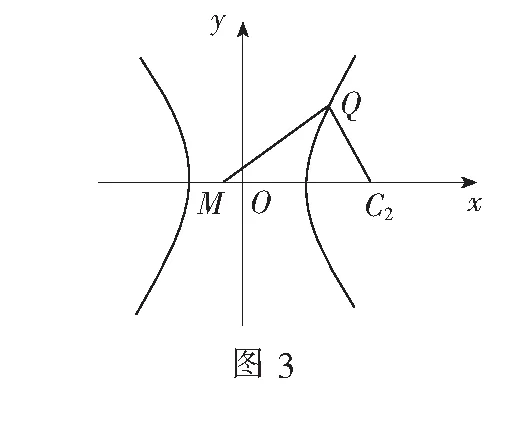
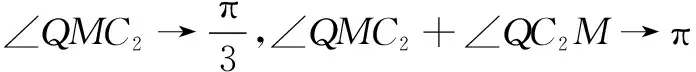
以下证明：当m=-1时,恒有

∠QC2M=2∠QMC2.

当x0≠2时,

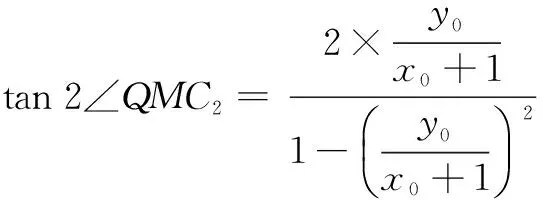
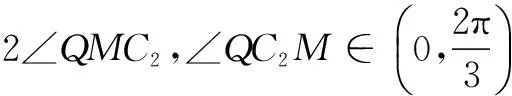
所以∠QC2M=2∠QMC2.

故存在λ=2,m=-1,使得∠QC2M=2∠QMC2.

评注探索某代数式的值为定值,通常是先把这个代数式表示出来,然后通过变量代换,将代数式化为只含一个变量的式子,进而化简得到代数式的值为定值.而探索两个角间的等量关系这类定值问题,只有求出了这两个角的大小,方可确定它们间的等量关系.这就需要借助这两个角的某三角函数值(如角的正切值)间的关系,来确定角间的等量关系,由于这类问题常常是含有参数的问题,还有可能用到两角和与差的三角公式,变形与化简都不是很容易的.若能另辟蹊径,从特殊情形入手,先猜后证,定是别有洞天.

可见,在处理解析几何中的定点、定角、定值问题时,如果运用正向思维处理感到不易上手,或感觉运算量过大,解题过程很繁琐时,可采取迂回战术,以退为进,退一步从特殊情形:从特殊的点、特殊的直线、特殊的曲线、特殊的图形,特殊的位置入手,寻求定点、定角或定值,再对一般情形加以验证,就能在解题目标的引领下,有的放矢,将运动变化的问题巧妙解决.这样的求解策略,既简少了繁杂的运算量,又能极大地提升学生解题的自信心,使久攻不破的压轴题得到有效突破,可谓妙手回春.