一道中考压轴题的实验探究与推广
安徽省歙县中学
郑观宝 (邮编:245200)
一道中考压轴题的实验探究与推广
安徽省歙县中学
郑观宝(邮编:245200)
1 实验探究一 △EPQ是等腰直角三角形吗?
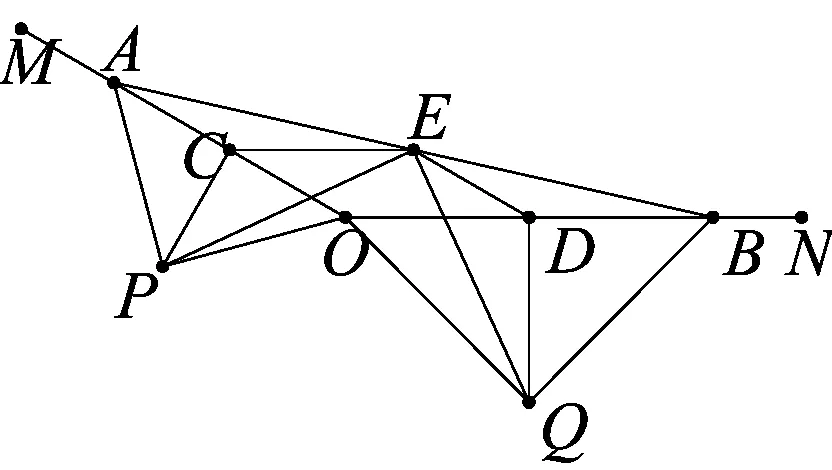
图1
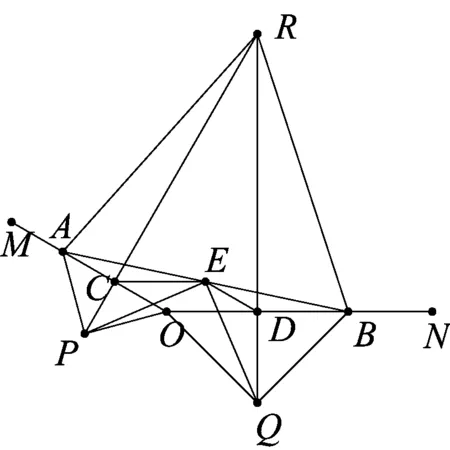
图2
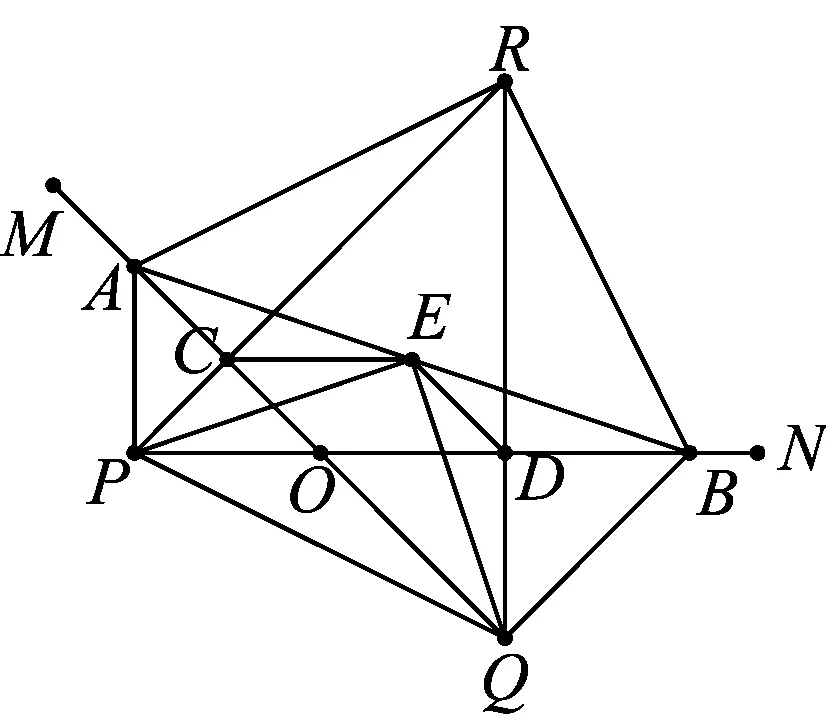
图3
问题(2016年安徽省中考压轴题):如图1,A、B分别在射线OM、ON上,且∠MON为钝角,现以线段OA、OB为斜边向∠MON的外侧作等腰直角三角形△OAP、△OBQ,点C、D、E分别为边AO、OB、AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC、DQ交于点R.
①如图2,若∠MON=150°,求证:△ABR为等边三角形;
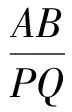
这是2016年安徽省初中毕业学业考试数学试题.限于篇幅,以下仅给出简略的证明过程.
(1)证明如图1,易得PC=CO=ED,CE=OD=DQ,∠PCE=90°+∠OCE=90°+∠ODE=∠QDE,所以△PCE≌△EDQ(边角边).
观察图1,能感觉到PE=EQ,且PE⊥EQ,这个猜想对吗?
实验一在《几何画板》中画出图4,度量∠PEQ的大小、线段PE、EQ的长度(如图4).
容易发现无论怎样改变钝角∠AOB的大小和OA、OB的长度,始终有PE=EQ,且∠PEQ=90°.
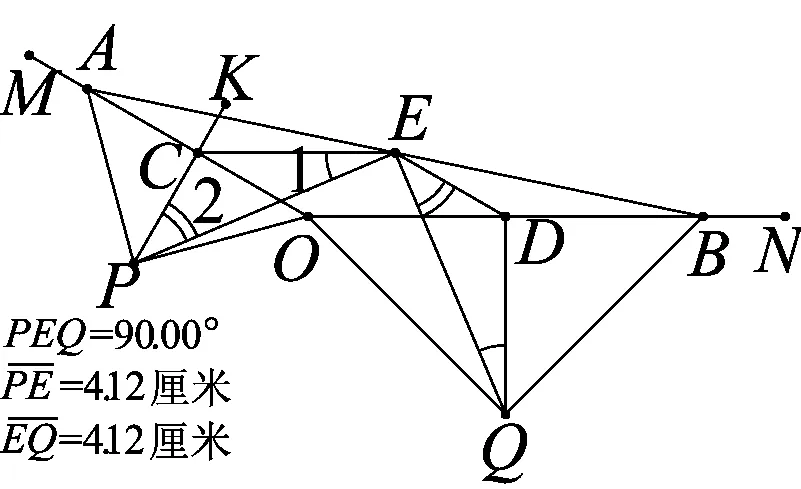
图4
证明延长PC到点K,设∠AOB=α,由△PCE≌△EDQ得PE=EQ显然成立,并且
∠PEQ=α-(∠1+∠2)=α-∠ECK=α-(α-90°)=90°.
可见,△PEQ始终是以PQ为斜边的等腰直角三角形.
2 豁然开朗的第二小题
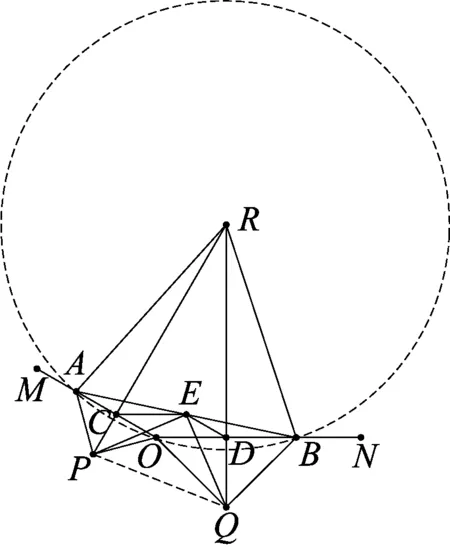
图5
由题可知,点R是△AOB两边OA、OB的中垂线的交点,因此点R为△AOB的外心,作出这个外接圆(如图5).
由圆的性质可得∠ARB=2(180°-α).
①要使等腰△ABR为正三角形,当且仅当∠ARB=2(180°-α)=60°,解得α=150°.
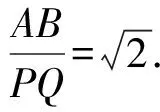
点评:有了上述探究与发现,第二小题就水到渠成,非常简单了!并且我们还得到如下一般性结论:如图2,分别以钝角△AOB(∠AOB为钝角)边OA、OB为斜边,向形外作等腰直角三角形△OAP、△OBQ,点C、D、E分别为边AO、OB、AB的中点,延长PC、DQ交于点R,则
(1)求证:△PCE≌△EDQ;
(2)△PEQ是以PQ为斜边的等腰直角三角形;
(3)当且仅当∠MON=150°时,△ABR为等边三角形;
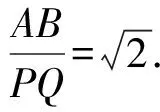
3 实验探究二 将“向形外作等腰直角三角形”推广为“向形内方向作等腰直角三角形”
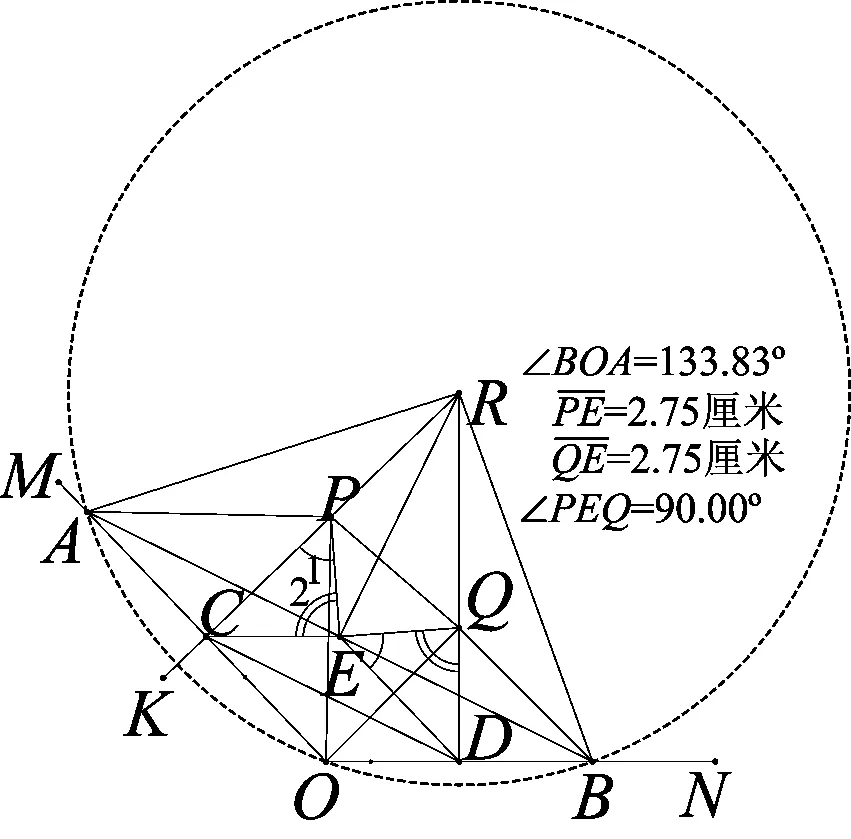
图6
实验二如图6,在《几何画板》作出满足题意的图形.不断改变钝角∠AOB的大小和线段OA、OB的长度,都能发现上述结论成立.下面证明这个发现:
(1)在△PCE与△EDQ中,易得PC=CO=ED,CE=OD=DQ,∠PCE=90°+∠OCE=90°+∠ODE=∠QDE,所以△PCE≌△EDQ(边角边).
(2)延长PC到点K,设∠AOB=α,由(1)得PE=EQ,且
∠PEQ=360°-α-(∠1+∠2)=360°-α-∠KCE=360°-α-(90°+180°-α)=90°.即△PEQ是以PQ为斜边的等腰直角三角形.
(3)同上可知,点R为△AOB的外心,作出这个外接圆(如图6).由圆的性质可得∠ARB=2(180°-α).
要使等腰△ABR为正三角形,当且仅当∠ARB=2(180°-α)=60°,解得α=150°.
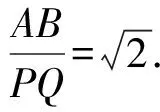
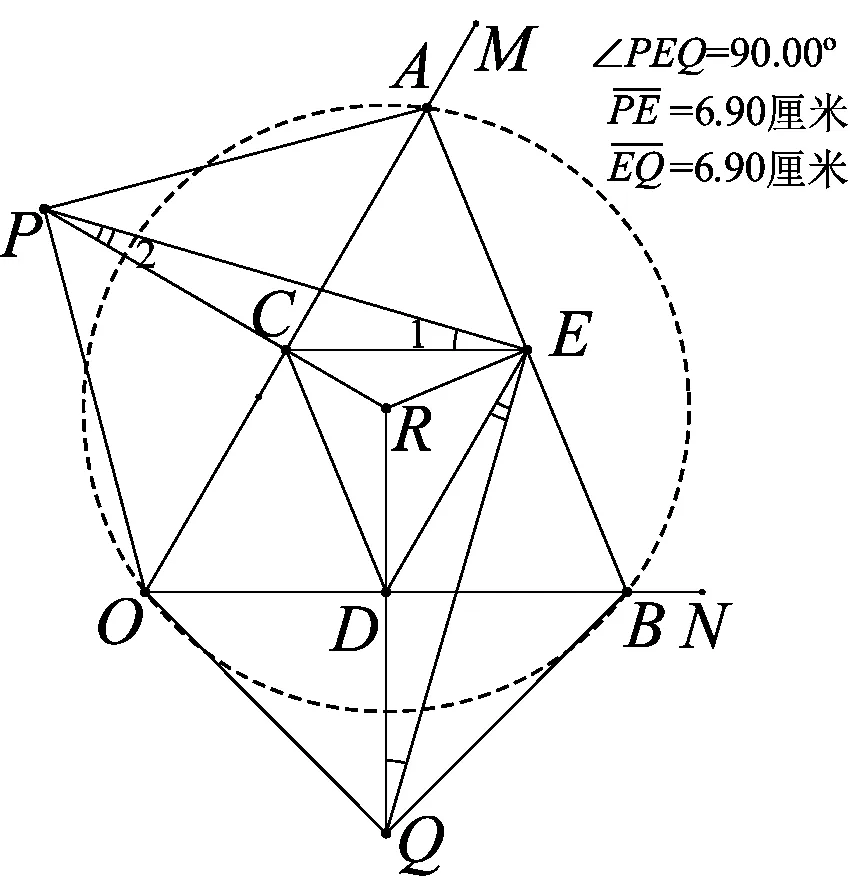
图7
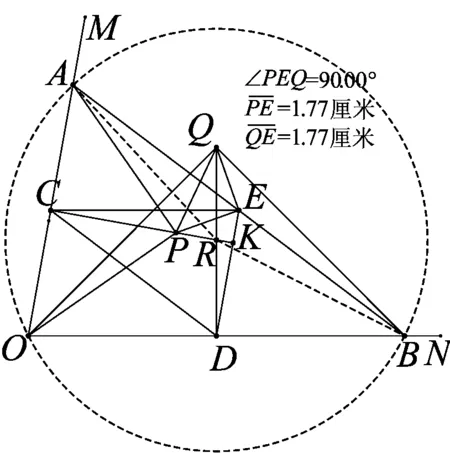
图8
4 实验探究三 将“钝角∠MON” 推广为“锐角∠MON”
实验三如图7、8,在《几何画板》作出满足题意的图形.不断改变锐角∠AOB的大小和线段OA、OB的长度,容易发现△PEQ始终为等腰直角三角形,下面证明这个发现(限于篇幅,证明过程以图8为例):
(1)如图8,在△PCE与△EDQ中,PC=CO=ED,CE=OD=DQ,∠PCE=90°+∠OCE=90°+∠ODE=∠QDE,所以△PCE≌△EDQ.
(2)延长CP交DE于到点K,设∠AOB=α,由(1)得PE=EQ,且
∠PEQ=∠DEQ-∠PEK=∠CPE-∠PEK=∠PKE=90°,即△PEQ是以PQ为斜边的等腰直角三角形.
(3)由于点R为△AOB的外心,作出这个外接圆.由于∠AOB为锐角,由圆的性质可得∠ARB=2α.
要使等腰△ABR为正三角形,当且仅当∠ARB=2α=60°,解得α=30°.
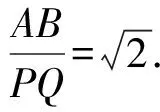
说明如果两个等腰直角三角形一个向形外作,一个向形内方向作,则没有相应的结论(实验过程这里略去).
5 实验探究之四 设∠AOB为钝角,将“向形外作等腰直角三角形” 推广为“向形外作相似等腰三角形”
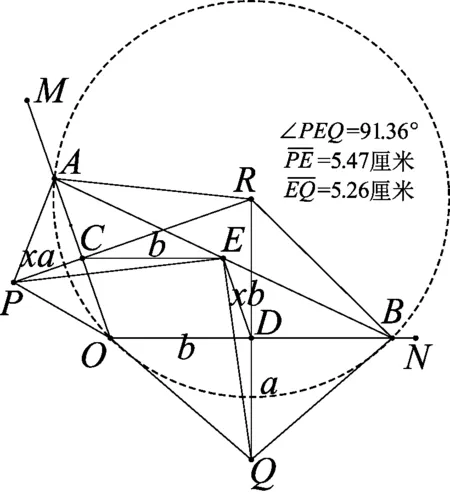
图9
实验四如图9,在《几何画板》中,以OA、OB(不是一般性,令OA≠OB)为底边向形外作两个相似等腰三角形.不断改变钝角∠AOB的大小和线段OA、OB的长度,容易发现:∠PEQ不一定为直角,且EP、EQ不一定相等.
(1)探究△PCE≌△EDQ的充要条件.
由于∠PCE=∠EDQ,所以要使△PCE≌△EDQ,必须PC=ED,CE=DQ⟹PC=CO,DQ=OD,则△OAP、△OBQ都是等腰直角三角形,即△PCE≌△EDQ,当且仅当△OAP、△OBQ都是等腰直角三角形.
(2)探究△PEQ是以PQ为斜边的等腰直角三角形的条件.
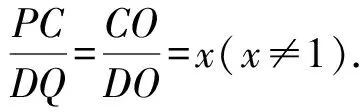
设∠PCE=∠EDQ=θ,DQ=a,DO=b,则PC=xa,CO=ED=xb,由余弦定理可得
PE2=x2a2+b2-2xabcosθ,PF2=a2+x2b2-2xabcosθ,两式相减得(x2-1)(a2-b2)=0.
由于x≠1,于是得a=b,即△OAP、△OBQ都是等腰直角三角形(余略).
综上所述,△PEQ是以PQ为斜边的等腰直角三角形的条件是△OAP、△OBQ都是等腰直角三角形.
(3)探究△ABR为等边三角形的条件.
当且仅当∠MON=150°时,△ABR为等边三角形(理由同前);
(4)探究△ARB∽△PEQ的条件.
由于RA=RB,所以EP=EQ,由(2)可得△ARB∽△PEQ的充要条件为△OAP、△OBQ都是等腰直角三角形,且∠MON=135°.
6 一系列实验探究
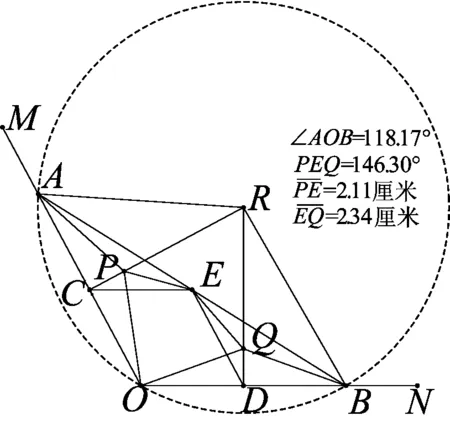
图10
1、实验五——设∠AOB为钝角,将“向形外作相似等腰三角形” 推广为“向形内方向作相似等腰三角形”.
如图10,在《几何画板》中,以OA、OB(不妨令OA≠OB)为底边向形内方向作两个相似等腰三角形.不断改变钝角∠AOB的大小和线段OA、OB的长度,容易发现:∠PEQ不一定为直角,且EP、EQ不一定相等.同上易证:
(1)△PCE≌△EDQ的充要条件是:△OAP、△OBQ都为等腰直角三角形;
(2)△PEQ是以PQ为斜边的等腰直角三角形的条件是△OAP、△OBQ都是等腰直角三角形;
(3)△ABR为等边三角形的充要条件是∠MON=150°;
(4)△ARB∽△PEQ充要条件为△OAP、△OBQ都是等腰直角三角形且∠MON=135°.
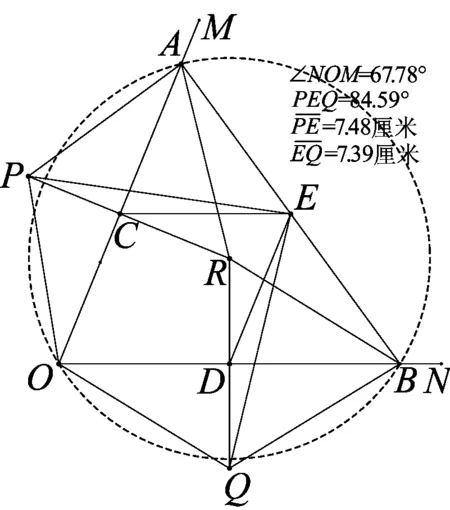
图11
2、实验六——将“钝角三角形” 推广为“锐角三角形”,向形外作相似的等腰三角形
如图11,在《几何画板》中,作锐角△AOB,以OA、OB(不妨令OA≠OB)为底边向形外作两个相似等腰三角形.不断改变锐角∠AOB的大小和线段OA、OB的长度,容易发现:∠PEQ不一定为直角,且EP、EQ不一定相等.同上易证:
(1)△PCE≌△EDQ的充要条件是:△OAP、△OBQ都为等腰直角三角形;
(2)△PEQ是以PQ为斜边的等腰直角三角形的条件是△OAP、△OBQ都是等腰直角三角形;
(3)△ABR为等边三角形的充要条件是∠MON=30°;
(4)△ARB∽△PEQ充要条件为△OAP、△OBQ都是等腰直角三角形且∠MON=45°.
3、实验七——将“钝角三角形” 推广为“锐角三角形”,向形内方向作相似的等腰三角形.
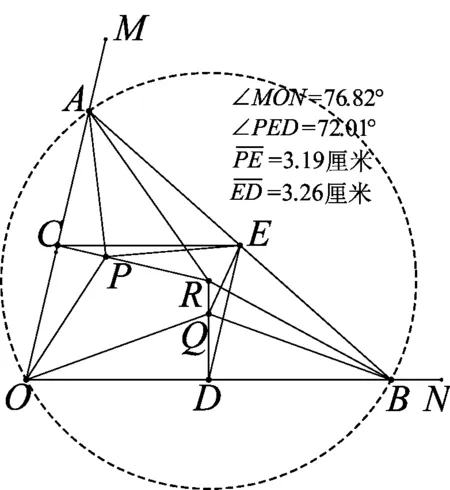
图12
如图12,在《几何画板》中,作锐角△AOB,以OA、OB(不妨令OA≠OB)为底边向形内方向作两个相似等腰三角形.不断改变锐角∠AOB的大小和线段OA、OB的长度,容易发现:∠PEQ不一定为直角,且EP、EQ不一定相等.同上易证:
(1)△PCE≌△EDQ的充要条件是:△OAP、△OBQ都为等腰直角三角形;
(2)△PEQ是以PQ为斜边的等腰直角三角形的条件是△OAP、△OBQ都是等腰直角三角形;
(3)△ABR为等边三角形的充要条件是∠MON=30°;
(4)△ARB∽△PEQ充要条件为△OAP、△OBQ都是等腰直角三角形且∠MON=45°.
综上所述,我们得到下列一般性结论:
结论以△AOB的边OA、OB为底边向形外(或形内方向方向)作两个相似等腰三角形△OBP、△OAQ,点C、D、E分别为边AO、OB、AB的中点,延长PC、DQ交于点R.则:
(1)△PCE≌△EDQ的充要条件是:△OAP、△OBQ都为等腰直角三角形;
(2)△PEQ是以PQ为斜边的等腰直角三角形的条件是△OAP、△OBQ都是等腰直角三角形;
(3)当∠AOB为钝角时,则△ABR为等边三角形的充要条件是∠MON=150°;当∠AOB为锐角时,则△ABR为等边三角形的充要条件是∠MON=30°;
(4)当∠AOB为钝角时,△ARB∽△PEQ充要条件为△OAP、△OBQ都是等腰直角三角形且∠MON=135°.当∠AOB为锐角时,△ARB∽△PEQ充要条件为△OAP、△OBQ都是等腰直角三角形且∠MON=45°.
可见,这道2016安徽中招考试试题仅仅是上述结论的一种非常特殊的情况.
本文系安徽省科学规划重点课题(编号:JG12316)研究成果.
2016-08-11)

