斜率等积面积定值——几道同源高考试题的探究

山东省单县第一中学

卫小国　　(邮编：274300)

安徽省太和中学

韩长峰　　(邮编：236600)



斜率等积面积定值
——几道同源高考试题的探究

山东省单县第一中学

卫小国(邮编：274300)

安徽省太和中学

韩长峰(邮编：236600)

研究2015年北京大学自主招生试题第14题，感觉问题似曾相识，经过探寻发现在近年高考中类似问题有2015年上海卷文科第22题理科第21题、2014年福建卷理科第19题.笔者经过解析高考试题、揭示问题背景、反思结论推广，终得圆锥曲线中在一定条件下“两直线斜率等积时，面积为定值”的性质，笔者现成文以供研讨.

1　典题解析

(2015上海卷文科第22题)已知椭圆x2+2y2=1,过原点的两条直线l1和l2分别交椭圆于点A、B和C、D.记△AOC的面积为S.(3)设l1和l2的斜率之积为m,求m的值，使得无论l1和l2如何变动，面积S保持不变.

整理得

k4-2mk2+m2=c2[2k4+(1+4m2)k2+2m2]，

由于等式对任意m恒成立，故

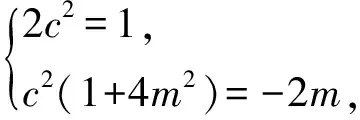
评注此题属高考热点问题之一的存在性问题，试题常以“是否存在”的形式出现而且结论不确定；问题常常需要由给定的题设条件探寻结论，或由问题追溯相应的条件.本题中关键是转化为恒成立问题，利用待定系数的方法确定c和斜率之积m的值.

2　背景探源

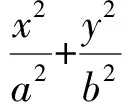
(1)充分性

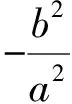
(2)必要性

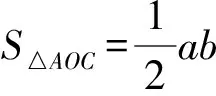
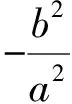
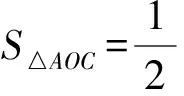
3　推广释疑

3.1结论推广，自招佐证

圆与椭圆的封闭特点，以上结论是统一的；虽双曲线有所不同，但同样具备两相交直线斜率等积，面积为定值.高考中也有考查此类同源问题，仅是命题形式有变.

文[1]对此题已有详细的解析，但笔者将结论进一步证明与推广：

上述的结论即是2015年北大自主招生试题的题根，自招试题为：

从O出发的两条射线l1、l2,已知直线交l1、l2于A、B两点，且S△AOB=c(c为定值)，记AB的中点为X,求证：X的轨迹为双曲线.

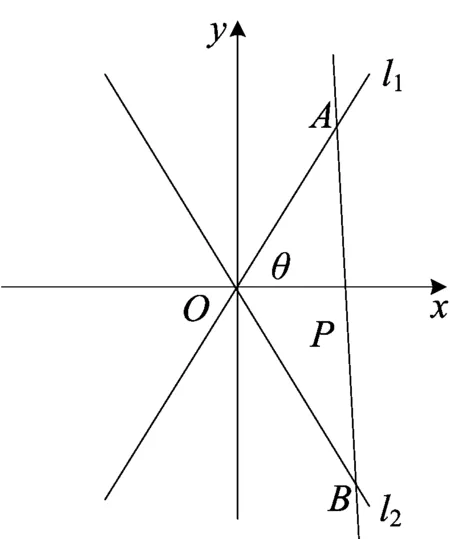
图1

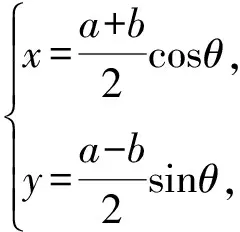
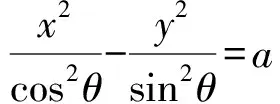
图2

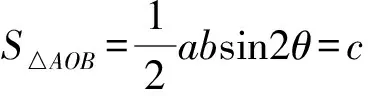
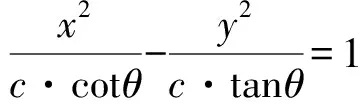
评注当S△AOB=c(c为定值)时，AB的中点的轨迹为双曲线；不难探究，当l1和l2的斜率之积为定值m时，△OAB的面积也为定值. 实质体现了“斜率定积”、“面积定值”与“轨迹定形”它们三者之间的内在联系. 因此自招题可变式为：“从O出发的两条射线l1、l2,已知直线交l1、l2于A、B两点，若l1和l2的斜率之积为定值m,记AB的中点为X,求证：X的轨迹为双曲线.”

3.2论证生疑，探究释疑

结论揭示在众多以l1、l2为渐近线的双曲线中，仅有唯一的双曲线使得△OAB的面积为定值，且取定值时直线l与其相切，笔者自然而生两点疑惑.

疑惑2当设过双曲线一点的某直线l′与共渐近线的另一双曲线相交于A、B，则△OAB面积有何特殊之处.

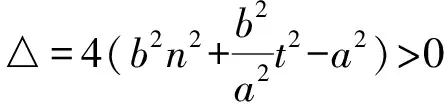
结合上述简单推导中，可知有进一步结论：

推理如下：

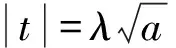
①

②

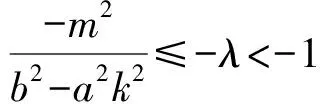
③

综上不难发现，S△OAB不为定值，但是存在最小值；可以归纳如下：

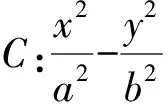
3.3类比推广，结论拓展

根据圆锥曲线的统一性，笔者探究发现，结论可以推广至一般椭圆，如下：

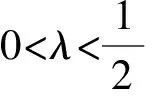
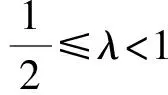
关于结论5的证明，类似于双曲线的探究疑惑2的推理论证，笔者在此不赘述.

4　典型应用

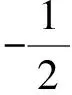
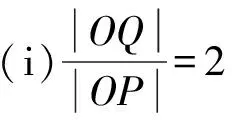
1李锋.不畏浮云遮望眼，除却繁华显真颜-2014年高考数学福建卷理科第19题背景探源及拓展[J].中学数学研究，2015(2)

2臧海鹏 孙焕彦.2015中国高考年鉴数学卷[M]．内蒙古少儿儿童出版社，2015

2016-06-06)