2016年高考山东卷文科第12题的解法探究及引申

江苏省苏州市第十中学

徐　青　　(邮编：215006)



2016年高考山东卷文科第12题的解法探究及引申

江苏省苏州市第十中学

徐青(邮编：215006)

每年高考结束，都会有一些不寻常的题目产生，因为这些题常常看似平淡，但其中却蕴含许多数学思想与方法，一些前因后果需要我们教者从其背后去思考、挖掘，探究出更多有价值的东西，使高考题真正发挥其应有的功能，下面以2016年一道高考题为例说明之．

1　试题呈现

(2016年山东省数学高考文科试题第12题) 观察下列等式：

……

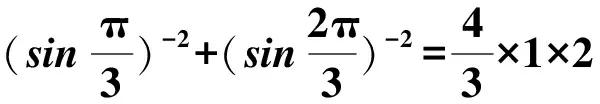
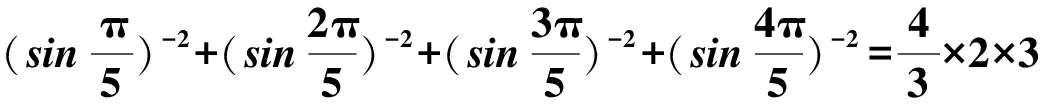
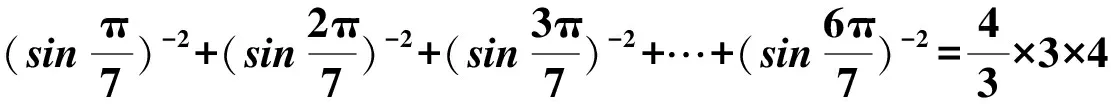
本题考查的是归纳推理问题，规律比较明显，题目不是太难，如果仅限于得出答案，对教师来说显然过于肤浅.我们应思考的是: 结论怎么证明，如果没有结论，在没有铺垫的情况下怎么推出答案，有一般的解决方法吗？还有没有类似的等式等等，笔者经过一番研究，得到一些结论，提供于此，供大家参考．

2　解法探究

下面先介绍一般的倍角公式：

因为(cosθ+isinθ)n=cosnθ+isinnθ，对左边用二项式定理展开，得

比较两边的实部及虚部，得

①

②

由②式，得

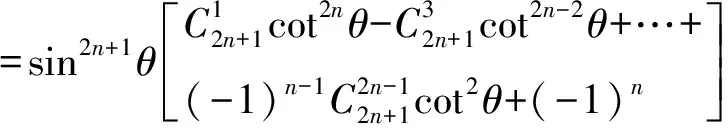
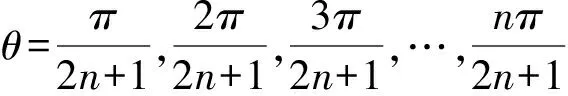
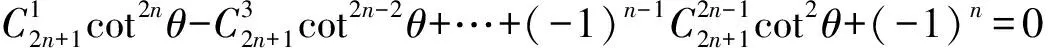
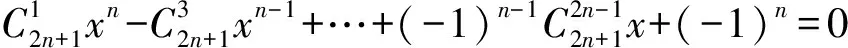
3　问题引申

(*)

于是

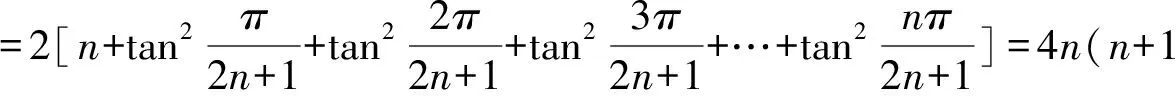
在方程(*)中，由韦达定理还可以得到若干等式，如：

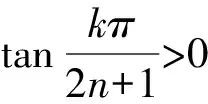
又如令n=3，4，… ，则可得不同的特殊三角恒等式．

由此，我们得到这类三角问题的解决方法：由一般的三角倍角公式，构造一个高次方程，然后用韦达定理得相应等式，在此过程中注意三角恒等变形．现将上述探究结果归纳如下：

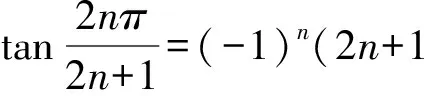
4　触类旁通

再据一般的倍角公式构造高次方程，根据韦达定理而得，自然联想到：

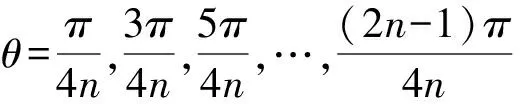
由公式①，得

(**)

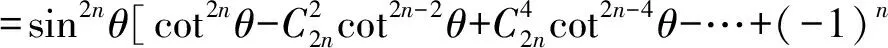
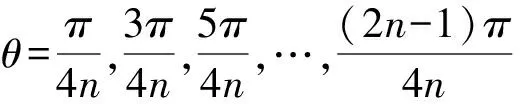
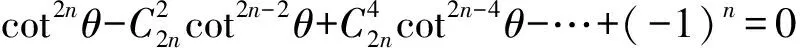
由韦达定理，得

同理可得

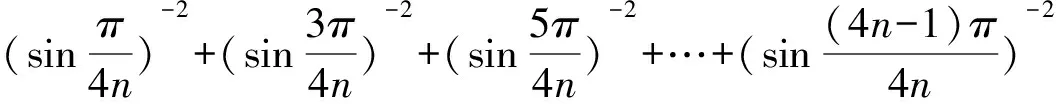
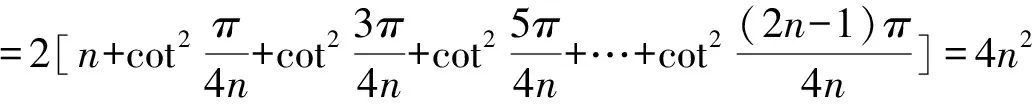
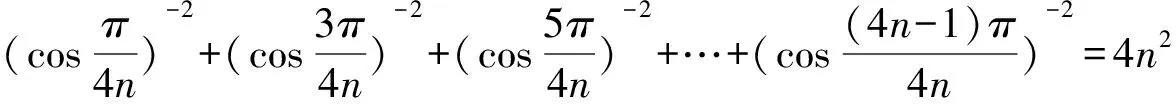
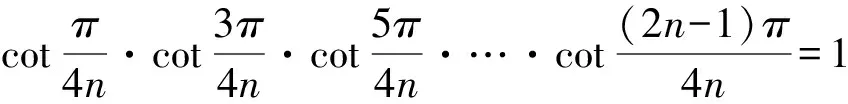
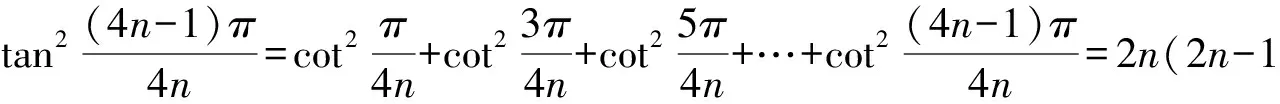
2016-07-06)