数列综合题分类解析

山东省枣庄二中 吴杰

数列综合题分类解析

山东省枣庄二中 吴杰

纵观近几年的高考，在解答题中，有关数列的综合型试题出现的频率较高，数列常与函数、方程、不等式相联系。这就要求同学们除了要能熟练运用有关概念、公式以外，还要善于观察题设的特征，联想有关的数学知识和方法，迅速确定解题的方向，以提高解数列题的速度。

一、等差数列与等比数列的综合问题

例1（2015年江苏卷）设a1，a2，a3，a4是各项为正数且公差为d（d≠0）的等差数列。

（1）证明：2a1，2a2，2a3，2a4依次成等比数列。

（2）是否存在a1、d，使得a1，a22，a33，a44依次成等比数列，并说明理由。

所以2a1，2a2，2a3，2a4依次构成等比数列。

（2）令a1+d=a，则a1，a2，a3，a4分别为a-d，a，a+d，a+2d（a>d，a>-2d，d≠0）。

点评解决等差数列与等比数列的综合问题，关键是理清两个数列之间的关系。如果同一数列中部分项成等差数列，部分项成等比数列，要把成等差数列或等比数列的项抽出来单独研究；如果两个数列通过运算综合在一起，要从分析运算入手，把两个数列分割开，弄清两个数列各自的特征，再进行求解。

二、数列与函数的综合问题

数列与函数的特殊关系，决定了数列与函数交汇命题的自然性。解决数列与函数综合问题的注意点：

（1）数列是一类特殊的函数，其定义域是正整数集，而不是某个区间上的连续实数，所以它的图像是一群孤立的点。

（2）转化以函数为背景的条件时，应注意题中的限制条件，如函数的定义域，这往往是非常容易忽视的问题。

（3）利用函数的方法研究数列中相关问题时，应准确构造函数，注意数列中相关限制条件的转化。

例2设fn（x）是等比数列1，x，x2，…，xn的各项和，其中x>0，n∈N，n≥2。

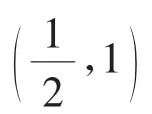
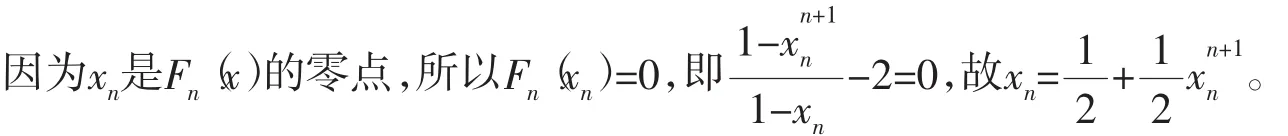
点评本题主要考查的是等比数列的前n项和公式、零点定理、等差数列的前n项和公式等知识点。解题时一定要抓住重要字眼“有且仅有一个”，否则很容易出现错误。证明函数有且仅有一个零点的步骤：①用零点存在性定理证明函数零点的存在性；②用函数的单调性证明函数零点的唯一性。

三、数列与不等式的综合问题

数列与不等式的综合问题是高考考查的热点。数列中不等式的处理方法：

（1）函数法：即构造函数，通过函数的单调性、极值等得出关于正实数的不等式，通过对关于正实数的不等式特殊赋值得出数列中的不等式。

（2）放缩法：数列中的不等式可以通过对中间过程或者最后的结果放缩得到。

（3）比较法：作差或者作商比较。

（4）数学归纳法：使用数学归纳法进行证明（在高二时学到）。

例3（2015年重庆卷）在数列{an}中，a1=3，an+1an+λan+1+μa2n=0（n∈N*）。

（1）若λ=0，μ=-2，求数列{an}的通项公式。

数列是考查同学们创新意识与实践精神的最好素材。从近些年的高考试题来看，一些构思精巧、新颖别致、极富思考性和挑战性的数列与方程、函数（包括三角函数）、不等式以及导数等的综合性试题不断涌现。这部分试题往往以压轴题的形式出现，考查综合运用知识的能力，突出知识的融会贯通。数列问题难度大，往往表现在与递推数列有关，递推含义趋广，不仅有数列前后项的递推，而且有关联数列的递推，更有数列间的“复制”式递推；从递推形式上看，既有常规的线性递推，又有分式、三角、分段、积（幂）等形式的递推。在考查通性通法的同时，突出考查思维能力、推理能力、分析问题和解决问题的能力。