等差数列前n项和Sn的最值问题
安徽省太和中学岳峻安徽省太和十一中 薛晓林
等差数列前n项和Sn的最值问题
安徽省太和中学岳峻安徽省太和十一中 薛晓林
等差数列是一种特殊的基本数列模型,常用Sn表示其前n项和。如何求解Sn的最值问题是高中数学的一个重要知识点,体现着函数与方程思想,也渗透着数形结合思想。
一、二次函数法

变式1已知等差数列-11,-9,-7,-5,-3,…的前n项和为Sn,求使得Sn最小的序号n的值。(答案:6)
二、邻项异号法
例2若数列{an}是等差数列,首项a1>0,a4+a5>0,a4a5<0,则使得{an}前n项和Sn取得最大值的正整数n是_______。
解析若d>0,因为a1>0,则{an}满足an>0,a4a5>0,与题意不符,所以d<0,
所以a1>a2>a3>a4>0>a5>a6>…
又因为a4+a5>0,a4a5<0,所以a4>0,a5<0,
故S4最大,即n=4时,数列{an}的前n项和Sn取得最大值。
点评对于公差不为0的等差数列{an},
若d>0,a1<0,且存在k∈N*,k≥2,使得ak≤0 若d<0,a1>0,且存在k∈N*,k≥2,使得ak≥0>ak+1,则Smax=Sk(ak>0)或Smax=Sk=Sk-1(ak=0)。 变式2已知等差数列{an}的通项公式为an=2n-31,若其前n项和为Sn,则Sn的最小值为。_______(答案:-225) 例3等差数列{an}中,a1>0,p≠q,Sp=Sq,当n取何值时,Sn取得最大值? 点评等差数列{an}的前n项和Sn可视为关于自变量n的二次函数,其定义域为N*,其图像是过原点的抛物线上的“自变量等距离分布”的孤立的点。若Sp=Sq(p、q∈N*,p≠q),则Sp+q=0。 变式3已知等差数列{an}的首项a1<0,设Sn为{an}的前n项和,且S6=S11,则Sn取得最小值时,n=。(答案:8或9) 例4已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn取得最大值的n是。 解析由于{an}为等差数列,所以a1+a5=2a3,a2+a6=2a4, 又因为a1+a3+a5=105,a2+a4+a6=99, 所以a3=35,a4=33, 故a1=39,d=-2, 所以an=a3+(n-3)d=35+(n-3)(-2)=41-2n, 方法1:Sn=n(40-n)=-(n-20)2+400,故使得Sn取得最大值的n是20。 方法2:an=41-2n,当n≤20时,an>0;当n≥21时,an<0。故使得Sn取得最大值的n是20。 方法3:Sn=n(40-n),显然有S1=S39,而Sn=n(40-n)的图像是抛物线上的孤立的点,根据抛物线的对称性,Sn取得最大值的n是20。 点评等差数列{an}的前n项和Sn的最值问题求解的方法有二次函数法、邻项异号法、图像法等。 变式4等差数列{an}的前n项和为Sn,S12>0,S13<0,当n=时,Sn取得最大值。(答案:6) 例5若{an}是等差数列,首项a1<0,a2015+a2016>0,a2015a2016<0,则使数列前n项和Sn<0成立的最大正整数n是。 根据数列{Sn}的图像所在的抛物线开口向上的特点,S4029<0且S4030>0,则使Sn<0成立的最大正整数n是4029。 点评求解等差数列的前n项和Sn<0成立时最大正整数n的问题,不是求Sn的最大值,而是求在所有使得Sn<0的正整数n当中,n的最大值。 变式5若{an}为等差数列,首项a1>0,a4+a5>0,a4a5<0,则使{an}的前n项和Sn>0成立的最大正整数n的值是。(答案:8)三、图像法


四、综合法
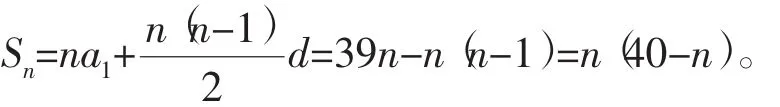
五、方法的拓展


