一种基于矩阵分解的电影推荐算法

聂常超

（南京理工大学 计算机科学与工程学院，江苏 南京210014）

一种基于矩阵分解的电影推荐算法

聂常超

（南京理工大学 计算机科学与工程学院，江苏 南京210014）

针对目前的电影推荐算法中，传统的矩阵分解算法对于用户的离散型评分数据集的数据利用率不高的问题，提出基于二项分布的矩阵分解算法的模型，在假定用户的评分数据是服从二项分布的前提下，利用最大后验估计学习得出损失函数，将用户的兴趣度作为影响因子，加入项目之间的邻域影响，其后利用随机梯度下降法针对问题求解。通过在MovieLens数据集上与传统的矩阵分解算法的对比实验，结果表明，提出的算法可以有效的提高推荐精度，表现出良好的稳定性。

推荐算法；二项分布；随机梯度下降；矩阵分解

飞速发展的互联网是现代社会人们获得信息的重要途径，与此同时，信息过载问题已经是网民必须要面对的一个问题。推荐系统就是为了解决信息过载问题［1］而提出的强有力的工具，同时也是目前学术界和互联网企业大力研究的热门问题。协同过滤推荐算法［2］在目前是使用最广泛的推荐算法，近些年来基于矩阵分解的推荐算法［3］越来越引起人们的重视。

目前的推荐系统中，用户对于电影的实际评分数据都是正整数，传统的矩阵分解算法不能对这些信息进行有效的利用，有鉴于此，提出了一种假设，即用户的评分数据服从二项分布。在此前提之下，从概率论的角度，假设模型中的参数都服从一定的分布模型，从机器学习的角度用最大后验估计［4］进行模型的推导，并将项目之间的相互作用加入到模型之中，矩阵分解模型因此更加健壮，具备更好的可解释性。

在MovieLens电影数据集上，对提出的算法和传统的矩阵分解算法进行实验对比的结果表明，所提出推荐算法可以有效提高推荐精度，并表现出较高的稳定性。

1　二项矩阵分解算法

传统的矩阵分解模型对于用户的评分并没有特别要求，因此有文献提出用户评分服从正态分布的矩阵分解（PMF）模型［5］。但在现实的评分系统中，用户的评分基本都是整数。因此，用户的评分服从正态分布的假定是不成立的。提出一种合理的假设，即用户的评分服从二项分布。并由此引出的二项分布矩阵分解模型［6］。

1.1二项分布模型

假设用户评分服从下面公式中的二项分布：

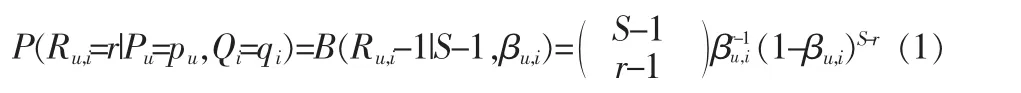
其中βu，i表示用户u对于项目i的评分概率。pu，qi分别满足正态分布并且相互独立。进一步假设在该二项分布中，对于不同u或i是相互之间独立的。因此，整个二项分布模型可以用如下形式表示：

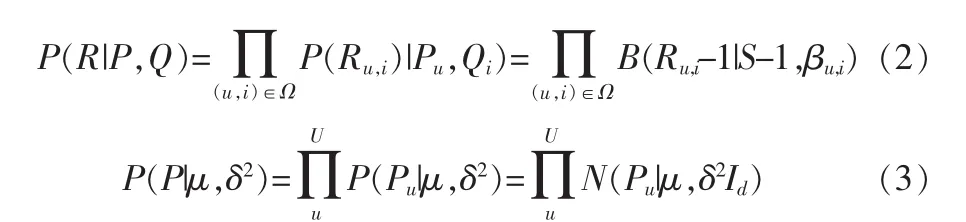
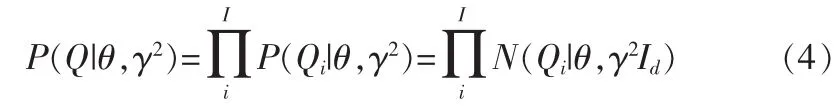
1.2最大后验估计学习

在统计学理论中，最大后验（MAP）估计方法是根据经验数据来获取难以观测到的变量的点估计，这在统计学中是一种比较常用的估计方法。最大后验估计与最大似然估计中的Fisher方法有密切的联系，但是最大后验估计使用了增大的优化目标，它将被估计量先验分布融合其中，据此，最大后验估计可被看作规则化的最大似然估计。

假定x是独立同分布的样本，θ为模型的调整参数，f是的模型，后验分布函数可以用下式表示：

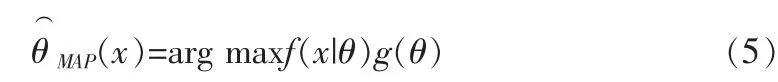
通过以上对最大后验估计的初步介绍，现在对式（2）求最大后验估计（MAP），将式（3）和式（4）代入得到：

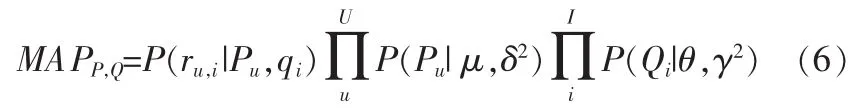
令μ=θ=0，将式（3）和式（4）代入，并加上ci，j的规则化项用以防止过度拟合，得到最后的目标函数如下：

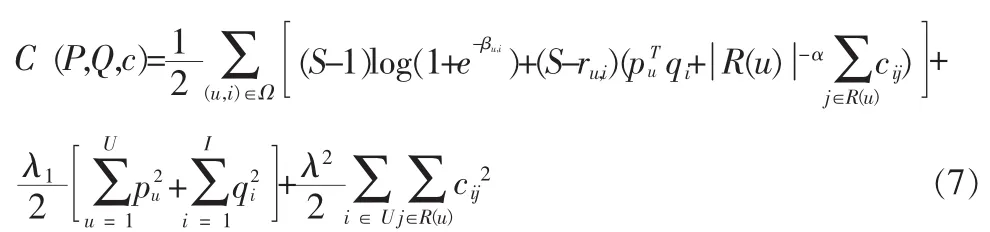
1.3随机梯度下降法

随机梯度下降法（SGD），在最优化理论中是最基础的算法之一。这种算法通过对参数求导的方法来找到目标函数的参数下降最快的方向，然后通过迭代求解来使目标函数逐步收敛。

对于式（7）中的目标函数，可以通过使用随机梯度下降法来进行求解。具体算法如下：

输入：用户评分矩阵R，隐含类别个数K。

输出：用户兴趣度矩阵P，项目隐类矩阵Q以及兴趣度偏移矩阵c。

（1）把实验数据集按照M:1的比例采用随机分配的方法分成训练集和测试集。

（2）选择合适的常量α，学习率η，以及正则化参数λ1，λ2的值，对用户兴趣矩阵P，项目隐类矩阵Q，兴趣度偏移矩阵c进行初始化。

6）根据公式（7）对P，Q，c分别求偏导得到更新规则，按如下方式分别更新P，Q，c矩阵：

7）对均方根误差RMSE进行计算，如果本次计算结果与上次结果之差的绝对值小于某一特定阈值，则迭代结束；否则，转到步骤3）。

2　实验与结果分析

2.1M ovieLens数据集

本实验所采用的数据集是GroupLens研究小组 （明尼苏达大学）提供的，包括MovieLens-100k以及MovieLens-1m两个数据集。MovieLens-100k数据集包括943个用户针对1682个商品进行的100 000条评分信息，MovieLens-1m数据集则包含了6 040个用户针对3 900个商品的1 000 209条评分记录，每个用户对20或20部以上的电影进行过评分，用户对每部电影的评分为5个等级（1到5分）。除了有评分信息之外，数据集中还包含有用户信息，电影信息，对电影评分的时戳等信息。即便如此，数据依然非常稀疏，在用户-项目的评分矩阵中，评分信息只有6.3%。

本实验中，会把数据集随机分成M份，把其中的一份作为测试集来用，另外M-1份则作为训练集。训练集用来进行相应的实验，测试集用来统计相应的评价指标。实验一共进行M次，M次实验结果的平均值将作为最终的评测指标，这样可以防止评价结果过拟合。

2.2实验分析

本实验采用RMSE（RootMean Square Error，即均方根误差）作为评价推荐系统的指标。均方根误差计算评分和实际评分之间误差的平方和的均值的平方根。RMSE的值如果越小，则说明精度越高。RMSE的计算公式如下：

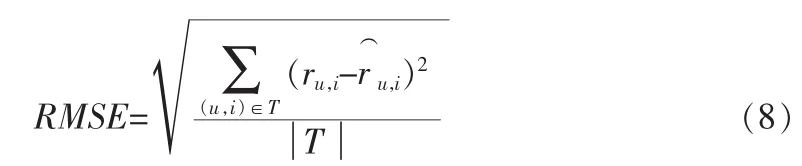
其中ru，i表示的是用户u对于项目i的真实评分，表示的是预测评分，T表示测试集，表示测试集的大小。

为了比较传统的矩阵分解算法与所提出的二项矩阵分解算法的异同，这里提出3种方法来进行对照实验：

1）规范化矩阵奇异值分解Funk-SVD

2）非负矩阵分解NMF

3）改进的二项矩阵分解BMF

其中第三种是提出的方法。

首先在MovieLens-100k数据集上调整隐含因子的个数，比较隐含因子数K的不同对BMF和传统的矩阵分解算法的推荐效果。这里令学习速率η=0.01，正则化参数λ1=λ2=0.05，令α=0.5，将迭代学习率每次按照0.99倍的速度递减。让K的值分别取10、20、50、100、150、200、250、300、350、400、500等值，观察不同的K值对于推荐结果的影响。

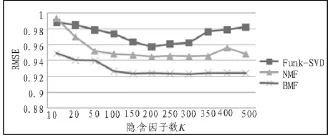
图1　3种算法随隐含因子数不同的RMSE值

图1中展示了3种不同的矩阵分解算法在隐含因子数K取值不同的情况下RMSE的情况。由图中可看出，当隐含因子数取200左右时，几种算法的结果最为理想。而当K值取更大时，计算复杂度随之增加，但是精度方面却没有明显改变。由图中还可看出，BMF具有良好的稳定性，当隐含因子数K改变时波动不大，在推荐精度方面，BMF要好于Funk-SVD、NMF，最好情况下，RMSE达到0.923 4。

表1中列出了几种算法在K=200的情况下在MovieLens-1m这个更大的数据集上的实验结果。从表中可看出BMF在学习率取值0.01的情况下，只需55次迭代就能达到最优值，RMSE最低达0.845 0。该实验表明，当数据集更大时，BMF优于其他两种矩阵分解算法。

表1　在MovieLens-1m数据集下3种算法的迭代次数和RMSE

3　结束语

随着近年来对于推荐算法的研究逐渐深入，越来越多的研究者开始关注矩阵分解算法。但是基于矩阵分解的推荐算法依然存在一些不足，如算法复杂度高，对用户数据利用率低等。针对现实中用户评分普遍具有离散性的特点，提出基于二项分布的矩阵分解算法和改进，在二项分布中考虑了邻域的影响，从概率方面对传统的矩阵分解方法进行改进。在MovieLens数据集下，对提出的算法和传统的矩阵分解算法进行了对比分析。实验表明，这种基于二项分布的矩阵分解推荐算法能够有效的提高推荐精度，具有较好的稳定性。

［1］许海玲，李晓东，吴潇.互联网推荐系统比较研究［J］.软件学报，2009，20（2）：74-80.

［2］周静.基于信任的协同过滤推荐算法研究［D］.秦皇岛：燕山大学，2013.

［3］JingLong Wu.Binomial Matrix Factorization for Discrete Collaborate Filterring［C］∥.DataMining，ICDM's09.Ninth IEEE international conference.［S.I.］:IEEE，2009:262-272.

［4］丁振国，陈静，吴金龙.基于关联规则的个性化推荐系统［J］.计算机集成制造系统，2003，9（10）：890-894.

［5］Li Pu，Faltings B.Understanding and Improving Relational Matrix Factorization in Recommender Systems［C］.Procee dings of the 7thACM conference on Recommender systems，New York:ACM，2013:41-48.

［6］陈天奇.基于特征的矩阵分解模型［D］.上海：上海交通大学，2013.

【相关参考文献链接】

陈小辉，高燕，刘汉烨.基于归一化方法的协同过滤推荐算法［J］.2014,22（14）：17-20.

魏婵娟，张春水，刘健.一种基于Cholesky分解的快速矩阵求逆方法设计［J］.2014,22（1）：159-161,164.

曹旭东，孙敬晶，张实.基于ARM及μC/OS-Ⅱ的RGB视频矩阵设计［J］.2014,22（2）：180-184.

张祎煊，殷新社，张燚.基于耦合矩阵修正和空间映射法的滤波器设计［J］.2015,23（1）；130-133.

马琳，王直杰，朱晓明，等 .基于灰度共生矩阵的注塑模具瑕疵检测［J］.2015,23（7）：138-140.

张卫华.基于矩阵的apriori算法的改进［J］.2015,23（13）：52-54.

曾弘扬.基于Epiphany计算并行矩阵乘法的研究［J］.2015,23（24）：52-55.

路振民，王阳，陆圣宇，等.基于矩阵键盘和QT/E的中文输入设计［J］.2016,24（4）：161-163.

张茗茗，周诠.基于修正正态分布的喷泉编码［J］.2015,23（19）：89-93.

彭鑫.一种基于稀疏矩阵的指纹识别新方法 ［J］.2014,22（23）：54-55.

徐彬，张建明.基于标签与协同过滤算法的淘书吧应用［J］. 2014,22（23）：21-23.

郭秀琪.基于本体的旅游资源推荐算法研究［J］.2016（6）：108-110.

袁小艳.基于情境的个性化学习云服务推荐模型研究［J］.2016（4）：39-41.

唐积益，黄树成.优化相似度计算在推荐系统中的应用［J］. 2015（23）:46-48.

史玉珍，郑浩.基于协同过滤技术的个性化推荐系统研究［J］. 2012（11）:41-44.

谭林，朱江，杨军，等.近地应用CCSDS标准LDPC码动态补偿译码算法研究［J］.2011（18）:36-38.

A movie recommendation algorithm based on matrix decomposition

NIE Chang-chao
（Computer Science and Engineering，Nanjing University of Technology and Engineering，Nanjing 210014，China）

For the currentmovie recommendation algorithm，the traditionalmatrix factorization algorithm score for the user's discrete data set is not high data availability problem，matrix decomposition algorithm based on the binomialmodel，on the assumption that the user data is to obey ratings under the premise of the binomial，using themaximum a posterioriestimation loss function study results，the user's interest degree as the impact factor，join neighborhood impact between projects，followed by the use of stochastic gradient descentmethod for problem solving.By the MovieLens datasetswith conventional matrix factorization algorithm comparison test results show that the proposed algorithm can effectively improve the recommendation accuracy，showing good stability.

recommendation algorithm；binomial distribution；stochastic gradient descent；matrix factorization

TN99

A

1674-6236（2016）19-0073-03

2015-10-21稿件编号：201510147

聂常超（1986—），男，河南新乡人，硕士研究生。研究方向：机器学习、计算机视觉。