结合Levenberg-Marquardt算法的垂直视差消减方法

李清玉，赵　岩，王世刚

(吉林大学 通信工程学院，吉林 长春 130012)



结合Levenberg-Marquardt算法的垂直视差消减方法

李清玉，赵岩*，王世刚

(吉林大学 通信工程学院，吉林 长春 130012)

垂直视差的存在是影响立体视频观视舒适度的主要因素。为了在不影响水平视差的条件下实现对垂直视差的消减，本文引入Levenberg-Marquardt(L-M)非线性算法实现变换矩阵的精确求解。首先用抗缩放、旋转及仿射变换的SIFT(Scale-invariant feature transform)特征匹配算法检测出双目图像对的特征匹配点，然后根据匹配点的坐标位置运用L-M算法计算可消减垂直视差的变换矩阵，将变换矩阵作用于目标图像，计算出该视图每个像素点的新坐标位置。实验结果表明：与利用线性算法求解二维射影变换矩阵的垂直视差消减方法相比，本文提出的求解方法在垂直视差消减上比该算法提高了约0.029 1～0.323 2个像素，对水平视差的影响比该算法降低了约0.118 7～1.139 1个像素。因此本文提出的方法对垂直视差的消减起到了优化作用。

SIFT；射影变换；垂直视差消减；Levenberg-Marquardt算法

1　引　言

近年来，随着3D技术的迅速发展，人们已经不满足于从二维图像中获得有限的信息，逐渐习惯于享受三维视觉带来的沉浸感[1]。双眼视差是立体显示技术的理论基础，水平视差在三维重建的过程中起着关键的作用，水平视差的变化使得人们对于画面所呈现的事物有了立体的感知，然而垂直视差则会使人感觉疲劳[2]。理想条件下，在拍摄过程中所有摄相机都应在同一条水平线上，同时要求所有摄像机的光轴平行，并且所拍摄出图像或视频的极线严格要求水平。但实际上，由于支架的形变及摄像机内部感光元件的不一致性等工艺问题往往会造成不同程度的垂直视差，这不仅影响了立体图像的合成质量，还会引起视觉疲劳。因此为了提高观视者的舒适度，垂直视差消减方法的研究成为了越来越多科研人员的研究重点[3]。

国内外对垂直视差消减技术的研究较少，并且这些方法中很多都是在处理过程中需要较多的图像信息或者摄像机参数[4]。韩国Yun-Suk Kang和Cheon Lee等人提出了针对平行相机阵列的拟合公共基线解决办法和针对弧形相机阵列的几何补偿校正算法。但是，这个方法需要多视点相机的标定参数，无法提供脱离相机参数的独立应用。在无摄像机标定情况下，Loop[5]提出了基于基本矩阵的图像校正方法，将校正过程分解为射影变换和仿射变换。该方法依赖于基本矩阵的精确求解，而由对应点计算基本矩阵还没有较为稳定的算法。上海大学刘利亮和安平[6]等人提出了一种基于公共点提取的多视图像校正的方法，该方法有效降低了垂直视差，但是在校正垂直视差的过程中使得水平视差也发生了较大改变。

针对上述问题，本文提出了一种基于Levenberg-Marquardt(L-M)算法的垂直视差消减方法，该方法不需要摄像机的参数和过多的图像信息，将由SIFT算法获得的匹配点通过L-M算法计算出较高精度的变换矩阵，在进一步消减垂直视差的同时降低了对水平视差的影响，从而减缓观看立体视频时产生的视觉疲劳。

2　算法实现

首先对双目图像对使用SIFT算法进行特征点匹配，然后根据匹配点坐标应用L-M算法进行校正变换矩阵的计算，并通过校正变换矩阵计算校正后像素的新坐标，生成校正后的视图。最后通过文献[7]的后处理方法去除部分图像中由校正变换引起的噪声。本文提出方法的流程图如图1所示。

图1　方法流程图 Fig.1　Flowchart of the proposed method

2.1图像的特征提取与匹配

本文采用SIFT[8]算法进行图像的特征提取与匹配，该算法是一种局部描述算法，它可以在图像中检测出特征点。在尺度空间中，它通过极值检测来查找潜在的兴趣点，由于采用了高斯微分函数，它不会受诸如图像的缩放、旋转及仿射变换的影响[9]。SIFT算法是目前图像特征匹配领域的研究重点，它的匹配结果十分准确，很少有偏差，而且效率很高。

2.2二维射影变换矩阵

射影变换就是射影平面上的可逆齐次线性变换，可以用3×3的矩阵来描述这个变换:

(1)

可以更简略地记为x′=H·x。

本文在坐标点的表述上使用了齐次坐标，即变换是齐次的，因而同一个射影变换矩阵可以相差一个非零常数因子，所以射影变换矩阵的元素所构成的8个比值，就可以确定这个射影变换矩阵。

Richard Hartley[10]对二维射影变换矩阵做了简要定义，如图2所示。一条射线由图像平面C上的一点x延伸，与世界平面Π相交于点xπ，这个点在图像平面C′上的投射点为x′。由平面Π引起的点x与x′之间的映射关系即射影变换。世界平面Π与两图像平面C和C′关系分别如下：

(2)

(3)

由式(2)和式(3)可整理出两个图像平面的单应性关系:

(4)

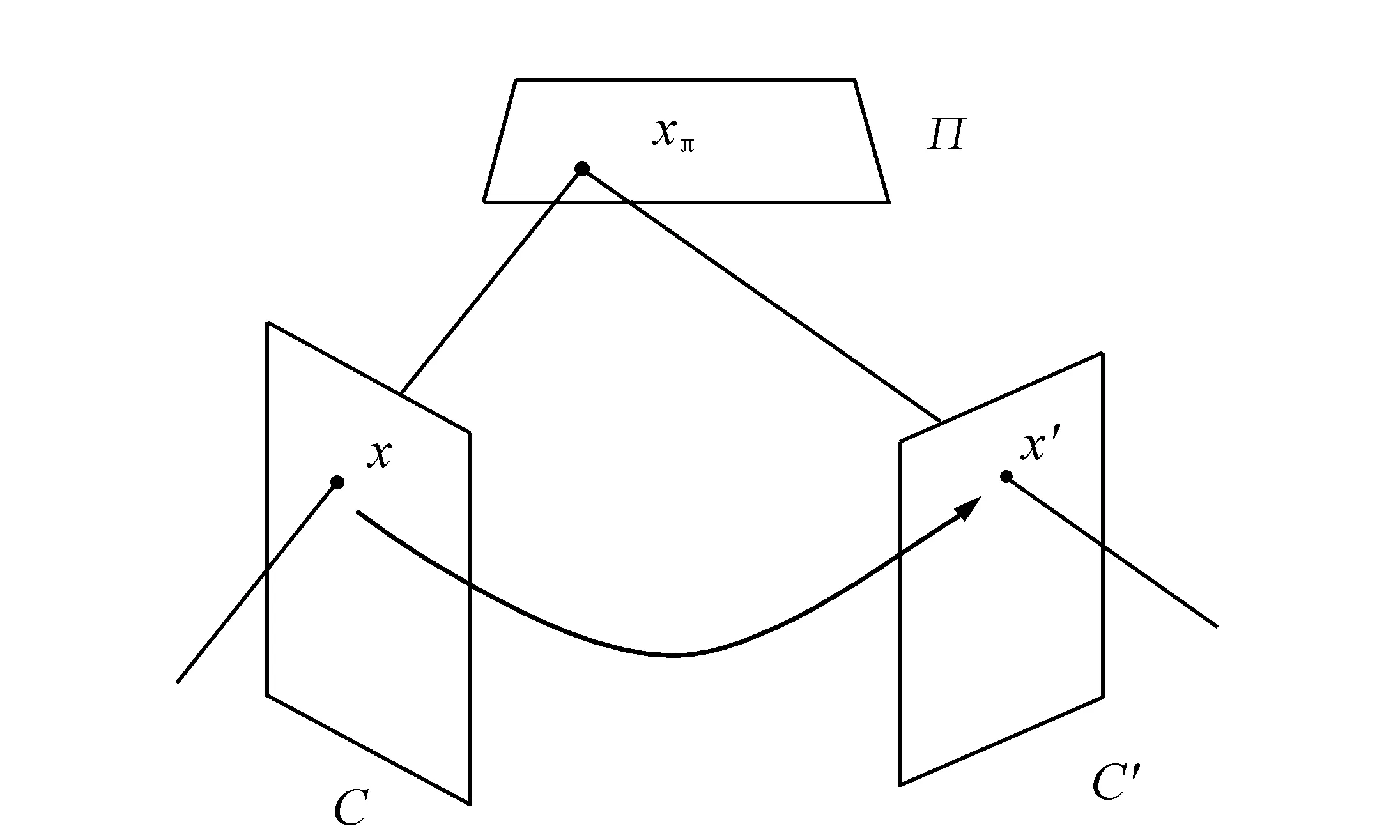
图2　射影变换定义 Fig.2　Definition of projective transformation

2.3垂直视差消减理论

假设左视图和右视图中的P(x,y)和Q(x′,y′)是一对特征匹配点，如果不存在垂直视差，那么Q的坐标值应为(x′,y)。同理，假设两幅图像使用SIFT算法检测出n对匹配点对，这些匹配点对的坐标形式整理为矩阵形式[11]:

前者作为基准图(左视图)上匹配点的二维坐标矩阵形式，后者为待处理的右视图上匹配点的二维坐标矩阵形式，可以得到消减垂直视差前、后的坐标矩阵应该分别为:

根据式(4)可以得到一系列的二维射影关系:

(5)

其中，二维射影变换矩阵为:

(6)

式中，采用齐次坐标方式，由式(5)通过L-M算法即可计算出二维射影变换矩阵 。

2.4L-M算法简介及在矩阵计算中的应用

L-M算法又称为阻尼最小二乘法，是目前应用较为广泛的一种无条件约束优化方法，该方法具有高斯-牛顿法的局部快速收敛特性，并克服了牛顿法不能有效处理奇异矩阵和非正定矩阵及对初始点要求比较苛刻的缺点；同时继承了梯度下降法的全局搜索特性，精确度很高[12]。

下面对L-M算法进行简要介绍：

设x(k)表示第k次迭代的权值和阈值所组成的向量，新的权值和阈值组成的向量x(k+1)可根据式(7)、(8)的规则求得：

(7)

(8)

(9)

式中，ei(x)为误差。对于高斯-牛顿法的计算法则有:

(10)

J(x)为E(x)的Jacobian矩阵。L-M算法是一种改进的高斯-牛顿法，它的形式为:

(11)

式(11)中，比例系数μ>0为常数,I为单位矩阵[13]。

当μ足够大时，总可以保证[JT(x)J(x)+μI]-1是正定的，从而保证其可逆，算法的每次迭代都对μ进行自适应调整。当接近解时，μ逐渐减小，权值调整类似于高斯-牛顿法，利用类似于二阶导数的信息，可以快速收敛到这个解；当远离解时，μ逐渐增大，权重调整又类似于梯度下降法，可以进行全局搜索。所以L-M算法同时具备了牛顿法和梯度法的优点，但计算J(x)要占用较多的内存[14]。

本文给出了一种应用L-M算法来迭代优化二维变换矩阵参数的方法。首先使用SIFT算法检测出匹配特征点对，再由垂直视差消减原理求出经过矩阵变化后的新坐标值，使用文献[6]的线性算法计算出二维变换矩阵的初值，通过L-M算法的不断迭代得到最后优化的二维变换矩阵参数。根据二维射影变换原理，可以将变换后的坐标和原始坐标表示成式(12):

(12)

式(12)中，m2表示水平方向位移量，m5表示垂直方向位移量，m0、m1、m3、m4表示尺度和旋转量，m6、m7表示水平和垂直方向的形变量。

由式(12)可得:

(13)

(14)

对于L-M算法，一个很关键的步骤就是设定误差指标函数，本文的目标是求解变换矩阵的8个参数的最优解，使得所有特征点的像点与其匹配点之间的距离之和最小。因此本文定义误差指标函数为:

(15)

则由式(9)可知:

(16)

式中，i=1,…,N,N表示点的个数，显然LM优化的结果是E(M)越小越好。

J(M)为ei(M)的Jacobian矩阵:

(17)

对e1(M),…eN(M)分别求出8个偏导数：

对m0求偏导:

(18)

为了简化下面公式的证明过程，将变量代换如下:

(19)

(20)

(21)

将式(19)、(20)、(21)定义的变量带入到求解Jacobian矩阵的过程中，则有:

(22)

(23)

(24)

(25)

(26)

(27)

(28)

设M为列向量(m0,m1,…m7)T,则：

(29)

(30)

J(M)上面已经求得，则JT(M)为J(M)的转置也已知，所以ΔM可以求出。其中I为单位矩阵，μ>0为常数，是一个试探性参数，对于给定的μ，如果能使误差指标函数E(M)降低，则μ降低，反之，μ增加。下面是具体的L-M优化算法的步骤：

①给出误差的允许值ε，常数β、μ以及初始化向量Mk,k=0。ε为两个像素，β=10,μ=0.001；

②利用变换矩阵Mk计算目标图像的新坐标，并计算误差指标函数E(Mk)；

③计算误差指标函数的Jacobian矩阵J(M);

④计算ΔM;

⑤若E(Mk)<ε，转到⑦；否则计算Mk+1，并计算误差指标函数E(Mk+1);

⑥若E(Mk+1)

⑦停止。

3　实验结果与分析

本文使用MatlabR2012b进行方法的仿真实现。实验采用的是分辨率均为1 024×768的立体视频测试序列“breakdancer”和“ballet”。

为了检验垂直视差消减的效果以及文献[6]和改进方法对水平视差的影响，利用检测出匹配点对的垂直视差的平均值eval和水平视差的平均值hori作为校正前后的评价标准：

(31)

(32)

式(31)中，eval值越小，说明垂直视差平均值越小，则观视者的立体观视感受越好[15]；式(32)中hori值与未处理过的原图像对的水平视差越接近[16]，说明在消减垂直视差的同时对水平视差的影响越小,则该垂直视差消减方法越好。

图3是对breakdancer立体视频序列第7帧的3、4视点进行垂直视差消减的实验效果图。其中(c)与(d)分别是利用文献[6]和本文提出的改进方法处理后的结果图。

表1是在不同参数设置情况下进行垂直视差消减前后的评价标准，eval是检测出匹配点对的垂直视差的平均值，单位为像素，用它来评价垂直视差消减的效果；hori表示检测出匹配点对的水平视差的平均值，单位同样为像素。

图3　breakdancer第7帧的3、4视点实验效果图 Fig.3　Experimental results of the 3 and 4 view points of the 7th frame of breakdancer image

参数原图像对eval值文献[6]方法eval值本文方法改进后eval值原图像对hori值文献[6]方法hori值本文方法改进后hori值0．252．68421．34181．30615．35534．07594．16520．402．60111．53301．51085．98915．45605．67910．502．68971．53191．50266．53026．14476．1882

在表1中，没有进行垂直视差消减的原始图像对在不同参数下的eval平均值是2.658 3个像素，hori平均值是5.958 2个像素。垂直视差消减后的eval平均值分别为1.468 9和1.439 8，使用本文方法改进后的结果比文献[6]中使用二维单应性矩阵方法提高了0.029 1个像素，比原始图像对提高了1.218 5个像素;垂直视差消减后的hori平均值分别为5.225 5和5.344 2，使用本文方法改进后的结果对水平视差的影响比文献[6]中降低了0.118 7个像素。

图4是对ballet立体视频序列的第1帧的1、2视点进行垂直视差消减的实验效果图。在表2中，没有进行垂直视差消减的原始图像对在不同参数下的eval平均值是7.750 9个像素，hori平均值是32.278 0个像素。垂直视差消减后的eval平均值分别为1.910 7和1.587 5，使用本文方法改进后的结果比文献[6]中使用二维单应性矩阵方法提高了0.323 2个像素，比原始图像对提高了6.163 4个像素;垂直视差消减后的hori平均值分别为29.162 7和30.301 8，使用本文方法改进后的结果对水平视差的影响比文献[6]中降低了1.139 1个像素。

图4　ballet第1帧的1、2视点实验效果图 Fig.4　Experimental results of the 1 and 2 view points of the 1th frame of ballet image

ballet图像序列的旋转现象比较严重，使用本文方法改进后的结果比文献[6]使用二维单应性矩阵方法提高的效果优于对breakdancer这类旋转程度不大的图像序列。

虽然在图3和图4的(c)和(d)中看不出明显的差别，但是从表1和表2中可以清晰地看出：通常情况下，选取不同参数时，在垂直视差消减方面，本文方法改进后的垂直视差比文献[6]使用二维单应性矩阵方法有所降低；在对水平视差的影响方面，本文方法改进后的立体图像对的水平视差相较于文献[6]的方法更接近于原立体图像对的水平视差，实现了在消减垂直视差的同时降低了对水平视差的影响。因此，使用本文改进方法比文献[6]的方法在垂直视差消减和对水平视差的影响两个方面均有所改善。而且图像的旋转程度越大，本文使用的方法对视差的调节越明显。

表2　不同参数下ballet垂直视差消减前后性能评价(单位：像素)

4　结　论

本文通过在二维变换矩阵的计算中引入L-M算法，从而实现了变换矩阵的精确求解。在垂直视差消减方面，本文提出的算法与文献[6]中使用二维射影变换的方法相比有了明显的提高。同时，在对水平视差影响方面，本文提出的方法与文献[6]相比更接近于原始图像对的水平视差。改进后的方法在垂直视差消减上比该算法提高了0.029 1～0.323 2个像素，对水平视差的影响比该算法降低了0.118 7～1.139 1个像素。对于旋转变换较大的图像，本文提出的方法改进更为明显。因此改进后的方法有利于在不影响水平视差的情况下对垂直视差的消减。

[1]杜歆,邹泷.视点合成中基于深度的空洞修复[J].浙江大学学报:工学版,2015,49(9):1616-1624.

DU X,ZOU L. Depth-based hole filling in view synthesis[J].J.ZhejiangUniversity(Engineering Science),2015,49(9):1616-1624.(in Chinese)

[2]王晓燕，王世刚，姜秀红，等.亮度优化立体视频视觉舒适度评价[J].中国光学，2015,8(3):394-400.

WANG X Y,WANG SH G,JIANG X H,etal.. Evaluation of stereo video visual comfort based on luminance optimization[J].ChineseOptics,2015,8(3):394-400.(in Chinese)

[3]李实秋,雷建军,周志远,等.基于SIFT匹配的多视点立体图像零视差调整[J].红外与激光工程,2015(2):764-768.

LI SH Q,LEI J J,ZHOU ZH Y,etal.. Zero-disparity adjustment of multiview stereoscopic images based on SIFT matching[J].InfraredandLaserEngineering,2015(2):764-768.(in Chinese)

[4]邵枫,姜求平,蒋刚毅,等.基于显著性分析的立体图像视觉舒适度预测[J].光学 精密工程,2014,22(6):1631-1638.

SHAO F,JIANG Q P,JIANG G Y,etal.. Prediction of visual discomfort of stereoscopic images based on saliency analysis[J].Opt.PrecisionEng.,2014,22(6):1631-1638.(in Chinese)

[5]LOOP C,ZHANG Z. Computing rectifying homographies for stereo vision[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Fort Collins,Colorado,USA,1999:125-131.

[6]刘利亮，安平，王贺,等.基于公共点提取的多视图像校正[J].信号处理，2011,6(27)：857-863.

LIU L L,AN P,WANG H,etal.. Multi-view images rectification based on common points extraction[J].SignalProcessing,2011,6(27):857-863.(in Chinese)

[7]ZHOU B L,ZHAO Y,WANG J Y,etal.. Improvement of visual fatigue based on vertical parallax elimination[C]. 2013 9th International Conference on Natural Computation,Shengyang,China,2013:1350-1354.

[8]DAVID G L. Distinctive image features from scale-invariant keypoints[J].InternationalJ.ComputerVision,2004(60):91-110.

[9]王灿进,孙涛,陈娟.局部不变特征匹配的并行加速技术研究[J].液晶与显示,2014,29(2):266-274.

WANG C J,SUN T,CHEN J. Speeding up local invariant feature matching using parallel technology[J].ChineseJ.LiquidCrystalsandDisplays,2014,29(2):266-274.(in Chinese)

[10]HARTLEY R. Theory and practice of projective rectification[J].InternationalJ.ComputerVision,1999(35):115-127.

[11]程明明，王贺，安平,等.基于特征点匹配的多视图像校正[J].液晶与显示，2010,8(24):593-597.

CHENG M M,WANG H,AN P,etal.. Multi-view images rectification based on feature points matching[J].ChineseJ.LiquidCrystalsandDisplays,2010.8(24):593-597.(in Chinese)

[12]姚佳宝,田秋红,陈本永.一种基于L-M算法的RANSAC图像拼接算法[J].浙江理工大学学报：自然科学版,2015,33(4):552-557.

YAO J B,TIAN Q H,CHEN B Y. RANSAC image stitching algorithm based on L-M algorithm[J].J.ZhejiangSci-TechUniversity(Natural Sciences),2015,33(4):552-557.(in Chinese)

[13]项文强,张华,王姮,等.基于L-M算法的BP网络在变压器故障诊断中的应用[J].电力系统保护与控制,2011,39(8):100-103.

XIANG W Q,ZHANG H,WANG H,etal..Application of BP neural network with L-M algorithm in power transformaer fault diagnosis[J].PowerSystemProtectionandControl,2011,39(8):100-103.(in Chinese)

[14]SHAO X T,SHAN L,ZONG M L. Levenberg-Marquardt algorithm based nonlinear optimization of camera calibration for relative measurement[C]. 2015 34th Chinese Control Conference(CCC),IEEE,Hangzhou,China,2015:4868-4872.

[15]邹泷.3D视频中的虚拟视点合成方法研究[D]. 浙江大学,2015.

ZOU L. Research on virtual view synthesis for 3D video[D]. Zhejiang University,2005.(in Chinese)

[16]高强,金杰,沈丽丽,等.使用EEG分析水平视差对3D图像舒适性的影响[J].红外与激光工程,2014(12):4140-4145.

GAO Q,JIN J,SHEN L L,etal.. Effect analysis of horizontal parallax on 3D images comfortableness using EEG[J].InfraredandLaserEngineering,2014(12):4140-4145.(in Chinese)

Method of vertical parallax reduction combined with Levenberg-Marquardt algorithm

LI Qing-yu, ZHAO Yan*, WANG Shi-gang

(College of Communication Engineering,Jilin University,Changchun 130012,China)*Correspondingauthor,E-mail:zhao_y@jlu.edu.cn

The existence of vertical parallax is the main factor of affecting the viewing comfort of stereo video. In order to reduce the vertical parallax without affecting the horizontal parallax, Levenberg-Marquardt(L-M) algorithm which is the nonlinear algorithm, is introduced in this paper to achieve the accuracy of the transformation matrix. Firstly, the SIFT algorithm, which is invariant to scaling, rotation and affine transformation, is used to detect the feature matching points from the binocular images. Then according to the coordinate position of matching points, the transformation matrix, which can reduce the vertical parallax, is calculated using Levenberg-Marquardt algorithm. Finally, the transformation matrix is applied to target image to calculate the new coordinate position of each pixel from the view images. The experimental results show that compared with the method that can reduce the vertical parallax using linear algorithm to calculate two-dimensional projective transformation, the proposed method using nonlinear algorithm improves the vertical parallax reduction from about 0.029 1 to 0.323 2 pixel and the effect of horizontal parallax is reduced from about 0.118 7 to 1.139 1 pixel. Therefore, the proposed method can optimize the vertical parallax reduction.

SIFT;projective transformation;vertical parallax reduction;Levenberg-Marquardt algorithm

2016-01-25；

2016-02-21

国家自然科学基金项目(No.61271315)

2095-1531(2016)03-0312-08

TN919.8

A

10.3788/CO.20160903.0312

李清玉(1989—)，女，辽宁葫芦岛人，硕士研究生，2012年于吉林大学获得学士学位，主要从事图像视频方面的研究。E-mail:597181451@qq.com

赵岩(1971—)，女，吉林辽源人，教授，博士生导师，2003年于吉林大学获得博士学位，主要从事图像与视频编码和立体视频处理方面的研究。E-mail:zhao_y@jlu.edu.cn

Supported by National Natural Science Foundation of China(No.61271315)