全面认识反函数

安徽省淮北一中　王洪洲

全面认识反函数

安徽省淮北一中王洪洲

反函数是一个较抽象的概念，而教材只给出一种描述性的定义，增加了我们理解反函数的难度。本文从反函数的有关性质、求法和巧妙应用等几个环节入手，对反函数进行全面认识。

性质1函数y=f（x）在某一区间上存在反函数⇔该函数在该区间上是一一映射。

性质2原函数的图像与其反函数的图像关于直线y=x对称。

性质3原函数的定义域是其反函数的值域，原函数的值域是其反函数的定义域。

性质5原函数与其反函数的单调性相同，原函数与其反函数的奇偶性相同。

一、反函数的存在问题

例1函数f（x）=x2-2ax-3在区间［1，2］上存在反函数，则a∈（）。

A.（-∞，1］ B.［2，+∞）

C.（-∞，1］∪［2，+∞） D.［1，2］

解析由性质1可知，函数f（x）=x2-2ax-3在区间［1，2］为单调函数，所以a∉（1，2），故选C。

评注函数y=f（x）在这一区间上单调与其在该区间上存在反函数不等价。

二、求反函数的问题

解析求反函数有三步骤。

步骤三：对调x、y，注明反函数的定义域，

评注求反函数的“三部曲”是基础，是理解反函数的“根”。

三、与反函数的定义域和值域有关的求值问题

例3函数f（x）=x2-1（x≥1）的反函数为y=f-1（x），则y=f-1（2）的值为（）。

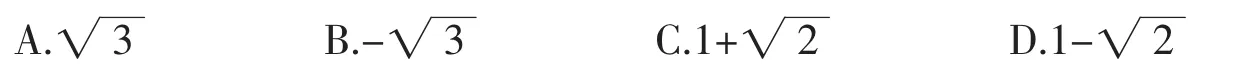
解析函数f（x）=x2-1的定义域是［1，+∞），值域是［0，+∞），

选项B、D都不对。

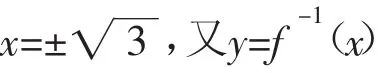
四、与反函数图像有关的问题

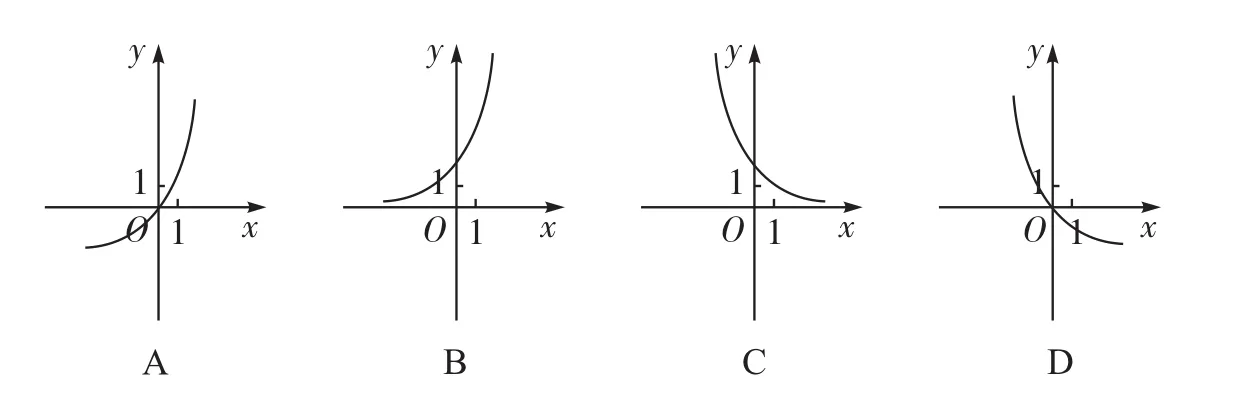
例4已知函数y=log2x的反函数是y=f-1（x），则y=f-1（1-x）的图像是（）。

五、反函数的巧用

例5对定义在区间I上的函数g（x），记g（I）=｛y|y=g（x），x∈I｝，已知定义域为［0，3］的函数y=f（x）有反函数y=f-1（x），且f-1（［0，1））=［1，2），f-1（（2，4］）=［0，1），若方程f（x）-x=0有解x0，则x0=_______。

解析由性质1和性质3可知：

当x∈［0，1）时，f（x）∈（2，4］；x∈［1，2）时，f（x）∈［0，1）。

而y=f（x）的定义域为［0，3］，

故当x∈［2，3］时，f（x）的取值应在（-∞，0）∪［1，2］∪（4，+∞）中。

故若f（x0）=x0，只有x0=2。

A.［1，e］B.［1，1+e］C.［e，1+e］D.［0，1］

所以存在x∈［0，1］，使f（x）=x有解，

化简为x2-x+a=ex，

令F（x）=x2-x+a，G（x）=ex，x∈［0，1］

若上式成立，则y=F（x）与y=G（x）的图像有交点。如右图，a即为y=F（x）与y轴交点的纵坐标，随着a的变化，y=F（x）的图像上下移动。数形结合可得a∈［1，e］，故选A。

在对应过程中，反函数中的变量关系与原函数发生了反向变化。反函数提供了观察变量关系的一个新视角。对反函数知识的学习能激活发散思维，培养创新意识。