非线性非方广义系统降阶Kalman状态估值器
田行伟,石 莹,高 阳,蒋函彤,王子宁
(1. 哈尔滨学院 工学院,哈尔滨 150086;2.黑龙江大学 电子工程学院,哈尔滨 150080)
非线性非方广义系统降阶Kalman状态估值器
田行伟1,石莹2,*,高阳1,蒋函彤1,王子宁1
(1. 哈尔滨学院 工学院,哈尔滨 150086;2.黑龙江大学 电子工程学院,哈尔滨 150080)
利用Taylor级数展开法将非线性非方广义系统线性化,再利用奇异值分解方法将线性化后的非方广义系统降阶为等价正常系统;基于Kalman滤波理论,得到非线性非方广义系统Kalman状态预报器和滤波器。并给出了数值Matlab仿真算例,验证了所提方法的有效性。
非方广义系统;Kalman滤波;奇异值分解;Taylor级数展开
近年来,非线性系统状态估值问题一直是控制理论界研究的热点问题之一。关于非线性系统状态估值的研究成果不断涌现[1-10]。但这些成果,多数是针对非线性正常系统进行验证讨论,对于更复杂的非方广义非线性系统的讨论还很少涉及。因此基于经典Kalman状态估值理论,研究非线性非方广义系统降阶Kalman估值器有重要的理论价值。
利用Taylor级数展开方法,把非线性非方广义系统转化为线性非方广义系统;再利用奇异值分解理论,基于经典Kalman状态估值理论,得到非线性非方广义系统降阶Kalman预报器和滤波器。通过数值仿真算例,验证了Taylor级数展开和奇异值分解方法应用于非线性非方广义系统降阶Kalman状态估值器的正确性。
1 非线性非方广义系统降阶Kalman状态估值器
考虑随机非线性离散非方广义系统

(1)

(2)
其中k为离散时间,状态变量x(k)∈Rn,观测变量y(k)∈Rm,输入噪声w(k),观测噪声v(k)f(·),g(·)和h(·)对x(k)是可微的,M∈Rp×n是奇异常数矩阵,且rankM=r 假设1w(k)和v(k)是零均值相关白噪声 其中E为均值符号,T为转置符号,δkk=1,δkj=0(k≠j)。 假设2系统(1)和(2)是强可控的[10] (3) (4) (5) (6) 其中 (7) (8) (9) 由于rankM=r,根据矩阵奇异值分解,存在正交矩阵U∈Rp×p,V∈Rn×n,使得 (10) 式中Σ=diag(σ1,σ2,…,σr),σi(i=1,2,…,r)为矩阵M的奇异值。 (11) 推导系统得 (12) 分解得到 (13) (14) (15) 其中x1(k)∈Rr,x2(k)∈Rn-r,式(13)~式(15)为非方广义系统的奇异值标准形式。由式(14)可得 (16) (17) 将式(17)代入式(13)~式(15)得到一个r维子系统 (18) (19) 其中 经过Taylor展开和奇异值方法将非方广义系统(1)~(2)等价转换得到系统(13)~(15)。下文将针对系统(13) ~(15)给出Kalman预报器、滤波器。 定理1非线性非方广义系统(1)~(2)在假设条件1、2下,有降阶Kalman预报器为 (20) (21) (22) (23) (24) (25) (26) (27) (28) 证明:根据递推射影定理,对式(18)取射影得到 (29) 其中ε(k)是新息过程,对式(19)两边取射影得到 (30) 将式(19)代入上式并且由预报误差 有 (31) 由式(18)和式(31)有 (32) (33) 由上式推导得到 (34) 其中定义预报误差方差阵 (35) (36) 对式(18)取射影运算有 (37) 将式(34)~式(37)代入式(29)得到递推Kalman预报器 (38) (39) 引出递推预报误差阵方程 (40) (41) 由射影定理可知 (42) 得到 (43) 由式(17)取射影有 (44) (45) 下面推导得误差方差阵。 (46) (47) (48) 证毕。 定理2非线性非方广义系统(1)~(2)在假设条件1、2下,有降阶Kalman滤波器为 (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) 定理2证明过程与定理1相似,证略。 考虑非线性非方广义系统 (59) (60) 解:将非线性非方广义系统式(59)、式(60)经过Taylor级数展开线性化后得到 仿真结果见图1~图2,图1中实线为真值x(k),虚线为Kalman状态估值器。图2中实线代表预报器误差累积和,虚线代表滤波器误差累积和。由图2可见,非线性非方广义系统降阶Kalman滤波器估计精度高于预报器,验证了理论推导的正确性。 (a)x1(k)和Kalman预报器 (b)x2(k)和Kalman预报器 (c)x1(k)和Kalman滤波器 (d)x2(k)和Kalman滤波器 图1非线性非方广义系统降阶Kalman状态估值器 Fig.1Reduced-order kalman state estimators for nonlinaer nonsquare descriptor systems (a)x1(k)的Kalman估值误差累积平方和曲线 (b)x2(k)的Kalman估值误差累积平方和曲线 本文基于强可控和正则性条件,通过Taylor级数展开的方法,将非线性非方广义系统化为线性非方广义系统,进一步应用经典Kalman滤波理论,基于广义逆和奇异值理论,提出非线性非方广义系统降阶Kalman预报器、滤波器。通过数值算例仿真,验证了非线性非方广义系统降阶Kalman状态估值器的正确性。 [1]王俊明,丁川, 片锦香, 等. 饱和离散随机非线性系统的H-∞模型预测控制[J].哈尔滨理工大学学报, 2015, 20(1): 37-44. [2]葛哲学. 滤波方法及其在非线性系统故障诊断中的应用研究[D]. 长沙:国防科学技术大学, 2014. [3]Dong Hongli, Wang Zidong, Gao Huijun. On design of quantized fault detection filters with randomly occurring nonlinearities and mixed time-delays[J]. Signal Processing, 2012, 92(4): 1117-1125. [4]Ding Zhengtao.Differential Stability and Design of Reduced Order Observers for Nonlinear Systems[C]//2009 IEEE International Conference on Control and Automation, 2009: 1104-1109. [5]Feng Zhan-shen,Feng Chao-yi. The Invariance Principle of Singular Nonlinear Systems and Its Applications[C]//2009 World Congress on Computer Science and Information Engineering, 2009:102-106. [6]张卓奎, 陈慧婵. 广义离散随机非线性系统的递推算法[J]. 西安电子科技大学学报:自然科学版, 2007, 34(2): 317-321. [7]赵灵冬. 分数阶非线性时滞系统的稳定性理论及控制研究[D]. 上海:东华大学, 2014. [8]方勇纯,卢桂章,袁著祉. 非线性系统理论[M]. 北京:清华大学出版社, 2009: 5-90. [9]王俊,张卓奎,杨建飞. 带状离散随机非线性系统的状态估计[J]. 西北大学学报:自然科学版, 2006, 36(4): 537-539. [10] 李晓东,常晶.一类广义Kuramoto-Sivashinsky方程的Lie对称分析[J].黑龙江大学自然科学学报,2015,32(3): 297-301. Reduced order Kalman state estimators for nonlinear non-square descriptor systems TIAN Hang-Wei1, SHI Ying2,*, GAO Yang1, JIANG Han-Tong1, WANG Zi-Ning1 (1.SchoolofTechnology,HarbinUniversity,Harbin150086,China;2.SchoolofElectrcnicsEngineering,HeilongjiangUniversity,Harbin150080,China) Taylor series expansion is used to making the nonlinear non-square descriptor systems to be linearized, then using singular value decomposition method to reduced a normal system. Basing on Kalman filtering theory, the state Kalman filter and predictor for the nonlinear non-square descriptor systems are presented. The simulation example is given to show the correctness and effectiveness of the proposed algorithm. non-square descriptor systems;Kalman filter;singular value decomposition;Taylor series expansion 10.13524/j.2095-008x.2016.02.029 2016-05-05 国家自然科学基金资助项目(61174139);哈尔滨学院学生科研项目(HXS2015-0011) 田行伟(1983-),男,黑龙江哈尔滨人,讲师,研究方向:控制理论与控制工程,E-mail: tianhangwei2000@163.com;*通讯作者:石莹(1971-),女,河北安国人,教授,博士,研究方向:控制理论与控制工程,E-mail: shiying89@tom.com。 TP274.2 A 2095-008X(2016)02-0072-07








3 数值仿真算例
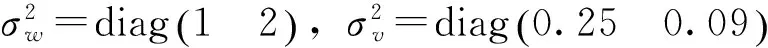






4 结 论

