兰新二线挡风板静载试验研究

田林杰，王起才，2，王元，杜迎东

（1.兰州交通大学土木工程学院，甘肃兰州730070；2.道桥工程灾害防治技术国家地方联合工程实验室，甘肃兰州730070）

兰新二线挡风板静载试验研究

田林杰1，王起才1，2，王元1，杜迎东1

（1.兰州交通大学土木工程学院，甘肃兰州730070；2.道桥工程灾害防治技术国家地方联合工程实验室，甘肃兰州730070）

新建兰州至乌鲁木齐第2客运专线，是世界上首条穿越大风区的高速铁路，设置合理可靠的挡风结构对于其运输安全有重大意义。本文依据钢筋混凝土结构计算的假设理论和计算方法，结合挡风板的受力特点，推导出挡风板的开裂弯矩、开裂时最大风荷载和跨中挠度计算公式，并采用合理的加载方式，对挡风板进行静载开裂破坏试验。试验值与计算值之间的对比结果表明，本文推导公式有较好精度，现场试验应用效果良好。

挡风板；开裂弯矩；最大风荷载；挠度；静载试验

兰新铁路是我国“八纵八横”铁路网主骨架之一，线路全长1 766 km，由于特殊的地理位置，兰新铁路第二双线需要穿越5大风区，穿越大风地区总长度近580 km［1］。由于风害是本线特有的困难和特殊问题［2］，通过设置防风结构解决大风区高速铁路防风技术难题，对兰新第二双线的顺利建成，建成铁路的运输安全乃至今后西部内陆地区的高速铁路建设均有重大意义。

沿线设立的L形挡风墙露在地面以上的部分体积小，占用路肩少，结构合理［3］。为了保证挡风板的可靠性，对挡风板进行静载试验，推出挡风板的开裂弯矩和发生开裂时的跨中挠度计算公式，为深入研究挡风板防治风害提供合理条件。

1　公式推算

1.1计算依据

试验表明，适筋混凝土梁正截面受弯的全过程可划分为3个阶段：未裂阶段、裂缝阶段和破坏阶段［4］。

1）第1阶段：混凝土开裂前的未裂阶段

开始加载时，由于弯矩很小，沿梁高的纤维应变随梁高呈直线分布，梁的工作情况与匀质弹性梁相似，应力与应变成正比。当荷载不断增大时，受拉区混凝土出现塑性变形，应力图形呈曲线。当荷载增大到某一值时，受拉区边缘混凝土达到其抗拉强度和抗拉极限应变值，截面处于开裂前的临界状态，称为第Ⅰa阶段。

2）第2阶段：混凝土开裂后至钢筋屈服前的裂缝阶段

截面受力达第Ⅰa阶段后，当荷载再增大时，截面开裂，混凝土原来承担的那一部分拉力转给钢筋，裂缝处混凝土不再受拉，裂缝截面中和轴位置上移，受拉区的拉力主要有钢筋承担。当荷载增大到某一值时，受拉区纵向钢筋达到其屈服强度，称为第Ⅱa阶段。

3）第3阶段：钢筋开始屈服至截面破坏的破坏阶段

钢筋屈服时，裂缝宽度扩展并沿梁高上移，中和轴继续上移，受压区高度进一步减小，此时受压区混凝土应变也迅速增长，塑性特征表现更为充分。当裂缝继续开展，受压区混凝土出现纵向裂缝时，混凝土被完全压碎，截面发生破坏，称为第Ⅲa阶段。

由于Ⅰa阶段混凝土没有开裂，受压区混凝土应力图是直线，弯矩与截面曲率基本上是直线关系，所以采用Ⅰa阶段作为挡风板抗裂程度的计算依据。

1.2基本假定

1）平截面假定：假定构件截面的应变沿截面高度呈线性分布［5］。

2）构件截面受拉区应力关系，可通过引入弹塑性高度比为1∶1的等效梯形模型［6］来分析。

3）受拉作用对混凝土构件影响很小，当构件出现裂缝时，混凝土平均拉应变其中，εtp为混凝土达到自身受拉强度时的应变。假设混凝土即将开裂时εtu=2εtp，且钢筋强度小于屈服强度，应力呈线性分布［7］。混凝土和钢筋的应力-应变关系如图1所示。其中，ftk为混凝土轴心抗拉强度标准值。

图1　材料应力-应变关系

4）构件邻近开裂时，由于钢筋应变εs很小，故看作和混凝土极限拉应变εtu相等［8］。

1.3计算公式

根据以上计算依据和基本假定，绘制如图2所示的挡风板截面计算图。其中，as，a's分别为挡风板受拉、压侧保护层厚度与对应受力钢筋半径之和；As，A's分别为挡风板受拉、压侧受力钢筋面积；h为挡风板高度；b为挡风板厚度；Xcr是裂缝即将出现时构件受压区高度。

据图2可计算出钢筋和混凝土的应变及应力。

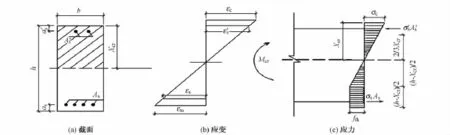
图2　挡风板截面计算图式

求解得到受压区高度

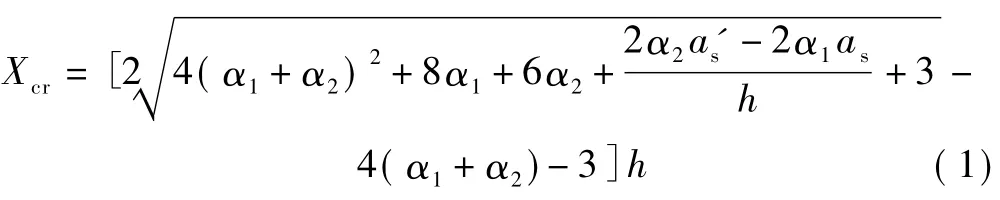
挡风板开裂时的弯矩

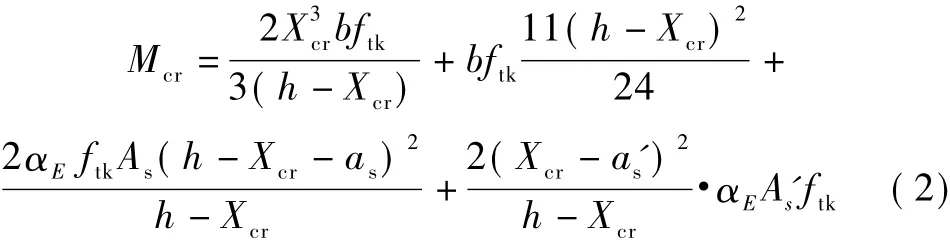
挡风板单元结构受力如图3所示。图3上部为挡风结构立面图，下部为挡风结构俯视图。由图可知，挡风墙由若干挡风板拼装而成，挡风板嵌入在两边的立柱卡槽内。

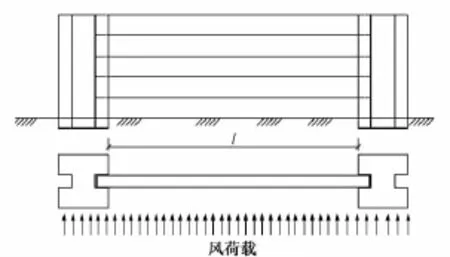
图3　挡风单元结构受力

在地形开阔平坦的地带，当均匀风速受阻时，风速将在挡风结构上重新分布［9］，按照底部为0，顶部最大的规律重分布。整个挡风板顶部均受到最大风荷载qf为最不利情况，把图3中两个立柱卡槽当做挡风板的约束支座，设挡风板高度为h，其计算简图如图4所示。

图4　挡风板受力变形简图

根据已推算出的挡风板开裂弯矩Mcr，可得挡风板发生开裂时的最大风荷载为

挡风板开裂时，跨中挠度为［10］

式中：E为挡风板弹性模量，由于挡风板配筋率较小，可近似用混凝土的弹性模量来代替钢筋混凝土的弹性模量；I为构件横截面对弯曲中性轴的惯性矩。

2　试验研究

2.1试验对象

本次静载试验选取4种不同规格的挡风板，具体参数如表1所示。挡风板混凝土强度等级为C35，钢筋采用HRB335级，受拉侧和受压侧混凝土保护层厚度相等。

2.2加载方案

作用于挡风墙上的力主要有水平风力、自重力、地基反力和地基水平抗力。考虑到横向加载难以实现，故将预制好的挡风板水平放置进行加载。水平放置要考虑结构的自重，加载总重减去结构的自重即为所加荷载值。根据现场的情况，选取钢板和砂袋对挡风板加载。试验采用3个应变片，均匀平行贴在试验挡风板跨中处下侧，挡风板内部埋置钢筋应力计。挡风板加载示意如图5。

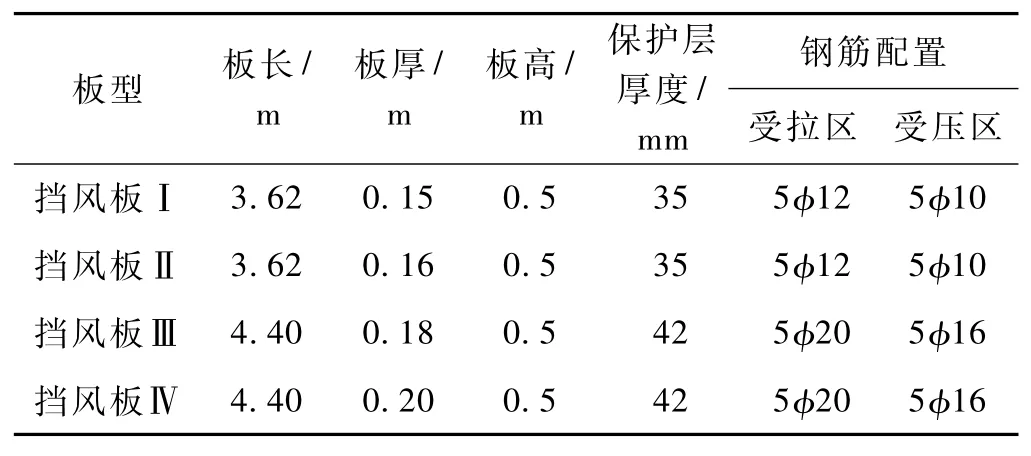
表1　挡风板规格

图5　试验挡风板加载示意

由于风荷载的脉动性较难模拟，为了能够准确反映荷载变化与板跨中位移、钢筋应变、混凝土应变的关系，采用逐级加载的方式加载，加载幅度根据式（3）计算的最大风荷载确定，依次为0.6qf→0.8qf→1.0qf→1.2qf→1.4qf→1.6qf→…→构件破坏→结束。加载至计算所得开裂荷载1.0qf时，应减小加载幅度，并随时观测构件开裂情况，记录构件开裂时的荷载值。

2.3试验结果

1）分析挡风板Ⅰ、挡风板Ⅱ、挡风板Ⅲ、挡风板Ⅳ在试验过程中所加荷载值和混凝土的拉应力关系，得图6所示曲线。

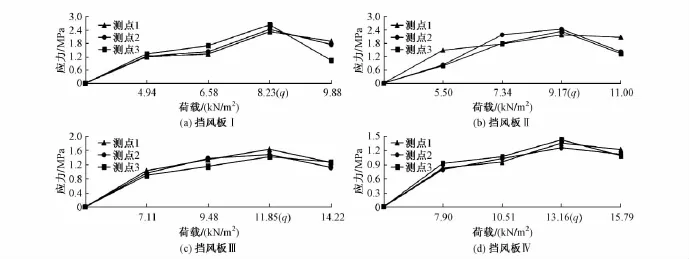
图6　挡风结构荷载-混凝土拉应力

2）比较挡风板开裂时的试验值和计算值，见表2。挡风板的最大风荷载qf的试验值与计算值比值的标准差为0.062，跨中挠度试验值与计算值比值的标准差为0.039，推导公式有较好的精度。

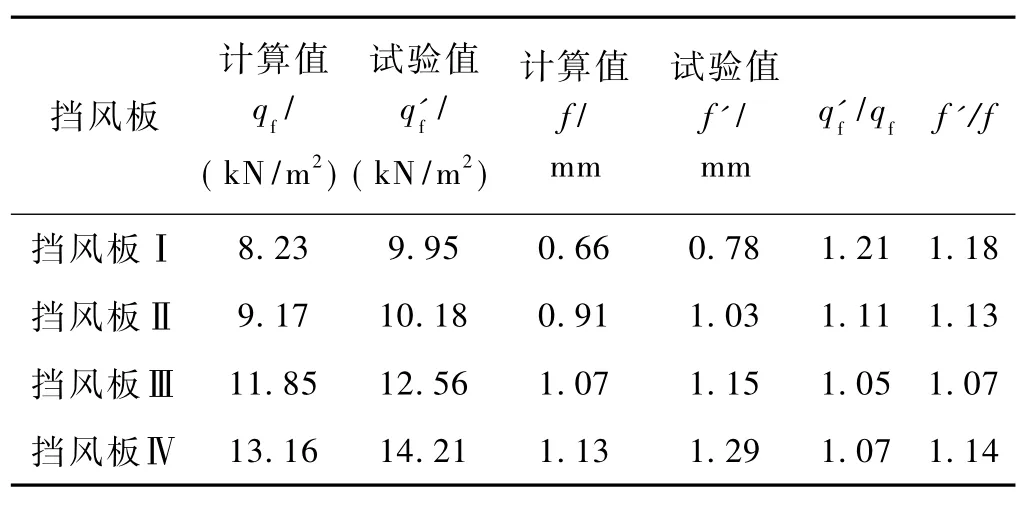
表2　试验结果

3）根据《铁路桥涵设计基本规范》（TB 10002.1—2005）［11］，风荷载强度按下式计算。

式（5）中：W为计算风压值；K1为风载体型系数，按照文献［11］表4.4.1取1.3；K2为风压高度变化系数，按照文献［11］表4.4.1取1.0；K3为地形地理条件系数，挡风结构尺寸不同，K3取值不同，这里取不同型号挡风结构中的最不利值1.4；W0为基本风压值，按W0= v2/1 600计算（v为风速，选取沿线的最大风速v= 60 m/s［12］）。得最大计算风压值4.1 kN/m2，均小于计算和试验所得使挡风板开裂的最大风压值qf和q'f，故挡风板的设计安全。

3　结论

本文依据已有关于钢筋混凝土结构计算的基本假定和计算公式，通过绘制挡风板结构受力图，推导出挡风板的极限开裂弯矩、发生开裂时的最大风荷载和跨中挠度的计算公式。依据挡风板发生开裂时的最大风荷载值，设置逐级加载方案，观测挡风板开裂前后的应力和挠度变化。通过对比分析挡风板开裂时的最大风荷载和跨中挠度的计算值与试验值可知，推导公式有较好的精度，现场试验效果良好。

［1］王争鸣.兰新高铁穿越大风区线路选线及防风措施设计［J］.铁道工程学报，2015，32（1）：2-3.

［2］贾国裕.兰新铁路大风灾害及其对策［J］.路基工程，2008，2（2）：195-197.

［3］孙成访，董汉雄，胡智炜.兰新铁路百里风区挡风墙设计［J］.铁道建筑，2009（6）：95-96.

［4］程文瀼.混凝土结构［M］.北京：中国建筑工业出版社，2005.

［5］高盈丹，丁自强.正截面抗裂计算的分析研究［J］.郑州工学院学报，1987，8（1）：29-30.

［6］过镇海，张秀琴.砼受拉应力-应变全曲线研究［J］.建筑结构学报，1988，4（4）：45-53.

［7］中华人民共和国建设部.GB 50010—2010钢筋混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［8］王元，王起才.防风板开裂弯矩计算及试验研究［J］.铁道建筑，2013（9）：6-7.

［9］王学楷.兰新铁路挡风墙的设计与施工［J］.路基工程，2012，28（5）：180-181.

［10］孙训方，方孝淑，关来泰.材料力学Ⅰ［M］.北京：高等教育出版社，2004.

［11］中华人民共和国铁道部.TB 100021—2005铁路桥涵设计基本规范［S］.北京：中国建筑工业出版社，2005.

［12］青兆麟，徐刚.挡风墙设计与结构形式探讨［J］.交通标准化，2013，3（3）：126-127.

（责任审编赵其文）

Static Loading Test Study on Windshield on Lanzhou－Xinjiang Second Railway

TIAN Linjie1，WANG Qicai1，2，WANG Yuan1，DU Yingdong1
（1.College of Civil Engineering，Lanzhou Jiaotong University，Lanzhou Gansu 730070，China；2.Road and Bridge Engineering Disaster Prevention and Control Technology National Local Joint Engineering Laboratory，Lanzhou Gansu 730070，China）

An new second passenger dedicated railway cross Lanzhou to Urumqi is the world's first high speed railway crossing wind region，so setting reasonable and reliable wind structure for transport safety is of great significance.Based on the theory and calculation method of the calculation of reinforced concrete structure，combined with the force characteristics of the wind shield，the formulae for calculating the cracking moment，maximum wind load and the mid-span deflection of the wind shield were derived.T he test of static cracking and failure of the windshield was carried out by using the reasonable loading method.T he comparison between the measured and calculated results show that the formulae have a better precision，field test has good effect.

W indshield；Cracking moment；M aximum wind load；Deflection；Static loading test

U213.1+54

A

10.3969/j.issn.1003-1995.2016.10.12

1003-1995（2016）10-0042-04

2016-05-30；

2016-07-25

长江学者和创新团队发展计划（IRT15R29）

田林杰（1992—），男，硕士研究生。

王起才（1962—），男，教授。