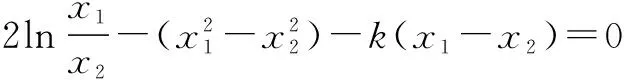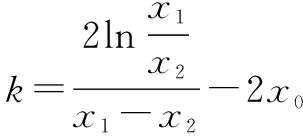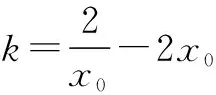培养学生创造性思维的两个途径

周儒东

(广东省高州中学，525200)



○数学教育○

培养学生创造性思维的两个途径

周儒东

(广东省高州中学，525200)

创造性思维,是指人脑对感知记忆的信息进行加工改选,并得出创造性结果的过程.创造性思维主要表现为在已有知识经验的基础上,创造性地发现问题,主动地提出自己的见解和新解决问题的方法.创造性思维要求学生在已有知识方法的基础上进行创新，不拘泥于已有的模式，敢于对问题及权威提出质疑等.这从两个方面要求教师在数学课堂上有针对性地培养学生的创造性思维能力.以下加以说明.

一、 利用归纳猜想，培养学生的创造性思维

归纳猜想的过程主要包括观察、归纳、猜想、证明等步骤.通过观察首先可激发同学们对知识的联想性思考,然后利用观察得到的结果进行归纳、猜想，由于归纳猜想的结论不一定正确，所以还要利用数学归纳法进行证明(适用于与自然数有关的命题).这是数学归纳法中技巧最强也是培养学生创造性思维能力中关键的一步.因为这一步能激发学生从各个角度、各个方面进行思索,并从中得到自己的结论,因此能激发学生大胆猜测、敢于探索的精神.

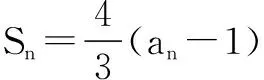
(1)求数列{an},{bn}的通项公式;

(2)确定an和nbn的大小关系,并给予证明.

解析第(1)问主要考察学生关于求数列的通项公式.本题可通过数列的前n项和与通项公式的关系来进行求解,很容易便得到:an=4n,n∈N*,bn=7n+3,n∈N*.此问题很好地反映了学生对一些公式的熟练程度.

对于第(2)问,很多学生首先可能想到的就是用类比的方法将an=4n转化为函数y1=4x(x>0),将nbn=n(7n+3)=7n2+3n转化为函数y2=7x2+3x(x>0),然后对两个函数进行比较,其中会用到求导的方法进行.这种创造性地解题老师应当给予肯定,并对学生进行鼓励,这样能有效地增强同学们对问题敢于探讨的信心,增进学生的创造性思维能力.然而老师也应指出这种方法的繁琐、不便于对该题的解答,接着从另一角度来分析该题:

首先，我们观察一下数列{an}、{bn}的前面几项的大小关系:当n=1时,a1=4,1·b1=10,∴a1<1·b1;当n=2时,a2=16,2·b2=34,∴a2<2·b2;当n=3时,a3=64,3·b3=72,∴a3<3·b3.通过这三项的计算及观察，比较多的同学就会猜想到an4·b4.这个不等式就推翻前面部分同学的猜想，这时就会让比较多的同学感到无从下手了.在此时老师应当给予适当的提示:同学们不妨再多计算两项看看．这样一来,同学们就会按照老师的要求继续进行计算:当n=5时,a5=1 024,5·b5=190,∴a5>5·b5;当n=6时,a6=4 096,6·b6=270,∴a6>6·b6.根据前6项的计算结果来看,同学们就会进行这样的归纳猜想:当n=1,2,3时，annbn.

为了证明上面的猜想,同学们就会用到数学归纳法来证明n≥4的情形,详解如下:

当n=4时,由上面的计算结果已表明结论是正确的.

假设当n=k(k≥4,k∈N*)时,ak>kbk,即4k>7k2+3k,4k+1>4(7k2+3k),则当n=k+1时,要证

4k+1>7(k+1)2+3(k+1),

只需证4(7k2+3k)>7(k+1)2+3(k+1).

所以，当n=k+1时， 不等式an>nbn成立.由以上可得,对一切n≥4,n∈N*,an>nbn.

综上所述,当n=1,2,3时,annbn.

本题主要通过“观察——归纳——猜想——证明”的步骤来引领同学们积极思考、大胆猜想、敢于探索.这不仅能让同学们摆脱已有的模式,跳出思维定向的影响,而且能直接培养同学们独立思考和创造性思维的能力.

二、利用正难则反，培养学生的创造性思维

很多事情都有两重性,数学也有.大部分同学在解题时经常是从问题的正面来思考,较少从问题的对立面入手,从而导致了思维定势,严重阻碍了创造性思维的形成.因此，教师在课堂中要注重从结论的对立面入手的教学方法,这样，不仅能让学生从更多的角度来对问题进行思考,而且更利于学生创造性思维的形成.

案例2已知函数f(x)=2lnx-x2-kx(k∈R),如果f(x)的图象与x轴交于A(x1,0),B(x2,0)(0

分析这是一道关于证明已知函数在某点的导数函数值不为零的题目.若是从题目的正面下手或结合函数的几何图形来求证是很难的,因为涉及到参数k,因此，从结论的反面来求证比较方便.首先对函数进行求导,然后假设f′(x0)=0,再结合已知条件中的f(x)的图象与x轴交于A(x1,0),B(x2,0)两点来列出相关方程,对方程进行简化并解答,最后找出矛盾,从而证明了原题目中的结论.详解如下:

解f(x)=2lnx-x2-kx(k∈R)，

设f′(x0)=0成立,且0

由①-②,得

⑤

∴u(t)在(0,1)上是增函数，

∴u(t)

这与⑤式相矛盾，

∴假设不成立，

∴f′(x0)≠0.

本题主要是先分析出从正面解答或从几何的角度来证明比较难,然后引领同学们从结论的着手.这不仅拓宽了学生的知识视野,避免定向思维的影响，活跃了同学们的思维,而且启发了同学从反面假设入手然后结合题目的条件找出矛盾来证明结论的独立思考方式,大大增强了同学们创造性思维的能力.