Measurement of residual stress in a multi-layer semiconductor heterostructure by micro-Raman spectroscopy

Wei Qiu·Cui-Li Cheng·Ren-Rong Liang·Chun-Wang Zhao· Zhen-Kun Lei·Yu-Cheng Zhao·Lu-Lu Ma· Jun Xu·Hua-Jun Fang·Yi-Lan Kang



RESEARCH PAPER

Measurement of residual stress in a multi-layer semiconductor heterostructure by micro-Raman spectroscopy

Wei Qiu1·Cui-Li Cheng1·Ren-Rong Liang2·Chun-Wang Zhao3· Zhen-Kun Lei4·Yu-Cheng Zhao1·Lu-Lu Ma1· Jun Xu2·Hua-Jun Fang5·Yi-Lan Kang1

Si-based multilayer structures are widely used in current microelectronics.During their preparation，some inhomogeneous residual stress is induced，resulting in competition between interface mismatching and surface energy and even leading to structure failure.This work presents a methodological study on the measurement of residual stress in a multi-layer semiconductor heterostructure.Scanning electron microscopy（SEM），micro-Raman spectroscopy（MRS），and transmission electron microscopy（TEM）were applied to measure the geometric parameters of the multilayer structure.The relationship between the Raman spectrum and the stress/strain on the［100］and［110］crystal orientations was determined to enable surface and crosssection residual stress analyses，respectively.Based on the Raman mapping results，the distribution of residual stress along the depth of the multi-layer heterostructure was successfully obtained.

✉ Wei Qiu qiuwei@tju.edu.cn

1Tianjin Key Laboratory of Modern Engineering Mechanics，Department of Mechanics，Tianjin University，Tianjin 300072，China

2Institute of Microelectronics，Tsinghua University，Beijing 100084，China

3College of Art and Sciences，Shanghai Maritime University，Shanghai 201306，China

4State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116024，China

5Graduate School of the Chinese Academy of Sciences，Beijing 100049，China

Residual stress·Multi-layer semiconductor heterostructure·Micro-Raman spectroscopy（MRS）· Strained silicon·Germanium silicon

1　Introduction

Strain is introduced into Si-based semiconductor devices to effectively promote carrier mobility and reduce thermal energy consumption［1］.The（biaxial and uniaxial）strain states and magnitudes directly determine the optical/electrical properties of such semiconductor devices［2］. Nevertheless，intrinsic and processing residual stresses are always introduced during the manufacture of Si-based structures coincident with the artificial strain［3］.With the realization of new design microelectronic structures and the application of new processing and manufacturing technologies，residual stress always presents a complex three-dimensionally inhomogeneous distribution inside the devices.Unlike metal materials，which can produce plastic shearing bands［4-6］，Si can only release residual stress through dislocation or cracking.Therefore，residual stress critically affects the optical/electrical functions and structural reliability of semiconductor devices［7］.

Several methods have been used to characterize residual stress and other mechanical parameters in thin films including the curvature method［8］，X-ray diffraction（XRD）［9］，and micro-Raman spectroscopy（MRS）［10］.Basically，the curvature method is applied through optical metrology such as electronic speckle pattern interferometry［11］and the digital image correlation method［12，13］，which measures the change in the curvature of the substrate before and after film deposition and calculation of the stress of the film using the Stoney equation［14］.This method only provides an aver-age stress value over the film area，and is not suitable for multilayer structures with asymmetric stress owing to its approximate algorithm of stress distribution.XRD can be used to measure stresses by detecting lattice deformation. However，it is difficult to use XRD for mechanical measurements on microelectronic devices owing to its inherent limitations in spatial solution and accuracy.

Because semiconductor materials usually have good Raman activity and Raman sensitivity to strain and stress，MRS has been regarded as an effective method of residual stress measurement on the micro-scale.It also has the advantages of high special resolution and being non-contact and non-destructive［15-17］.For instance，the work by De Wolf［18］analyzed residual stress distribution in Si-based IC grooves of micro-electro-mechanical systems（MEMS）caused by processing and the thermal stress distribution produced during the electronic packaging process.Also，a tip-enhanced Raman spectroscopy（TERS）system was used by Hayazawa et al.［19］to measure the stress of strained silicon layers on the nano-scale.In addition，the Raman shift to stress relationship of transverse isotropic materials was successfully studied（Li et al.［20］）and the residual stress in porous silicon films prepared by chemical and electrochemical corrosion was measured using MRS（Kang et al.［21］）. Then，MRS was used by Qiu et al.［22］to study the dynamic capillary evolution of a porous silicon surface.

Although several works have attempted to characterize the mechanical behavior of Si-based materials using Raman spectroscopy，there still remains a lack of systematic investigation ofa method formeasuring internalmechanicalbehavior，especially the distribution of residual stress near internal interfaces inside the materials.Furthermore，even though it has been widely accepted that preparing cross-section samples is an effective method to characterize mechanical and physical properties of three-dimensional inhomogeneity inside materials，the basic Raman-stress/strain relationship for such cross-sectional measurement is still unknown or misunderstood similar to that for surface measurement.

This paper presents a methodological study of residual stress measurementcarried outon a multi-layersemiconductor heterostructure using MRS.The material was composed ofa biaxialstrained silicon filmand germaniumsilicon buffer layers grown on a silicon wafer.Cross-section samples were prepared for the subsequent investigation of the material and mechanical properties inside the specimens.Scanning electron microscopy（SEM），transmission electron microscopy（TEM），and MRS were used to measure the geometric parametersofthe multilayerstructure.The Raman to stress/strain relationship of the［100］and［110］crystal orientations was obtained to allow residual stress analysis of the surface and cross-section，respectively.Based on the Raman mapping results，the distribution of residual stress along the depth of the multi-layer structure was obtained.

2　Materials and methods

2.1Materials and samples

The multi-layer semiconductor heterostructure material（ε-Si wafer for short）used in this work was prepared through reduced pressure chemical vapor deposition（RPCVD）［23］. Dichlorosilane（SiH2Cl2）gas was used as the Si source，germane（GeH4）as the Ge source，and H2as the carrier gas.A 5´´（001）monocrystalline silicon wafer substrate of 630 μm in thickness was used.Before epitaxy，the substrate was pretreated by steeping in 3:1 H2SO4:H2O2solution for 10 min to remove organic residues on the surface and then dipped in 1%HF solution for 45-50 s to remove the native oxide.The RPCVD growth temperature was 900◦C，and the chamber pressure was 1.33×104Pa.The germanium composition was increased linearly to form a graded germanium silicon（GexSi1-x，x=0→ 0.2）buffer layer of～3 μm thickness.The growth rate was then decreased and the germanium composition was held to obtain a relaxed germanium silicon（Ge0.2Si0.8）buffer layer of～1 μm thickness.Finally，a strain silicon cap layer of～15 nm was grown at 750◦C and 1.33×104Pa.The multilayer structure of the thereby obtained ε-Si wafers is shown in Fig.1a.

Fig.1 Schematic of a as-grown multi-layer structure and b crosssection sample

Cross-section samples were prepared to allow the accurate investigation of the internal material properties and mechanical behaviors of the multilayer structure.The crosssection samples（shown in Fig.1b）were prepared as follows.The ε-Si wafer was cut along the［110］direction into a number of rectangular pieces.Two of these pieces were pasted together with the ε-Si surfaces face-to-face using epoxy resin.Then，two C-Si pieces，cut from a 430 μmthick 2´´（100）monocrystalline silicon wafer，were pasted onto the outside of the two ε-Si pieces.After the epoxy resin was totally curved，the pasted group was cut，along its cross-section，into several thin slices with about 1 mm in thickness.All the new cross-section surfaces of each slice were polished with sandpaper with mesh numbers increasing from 600 to 10000 and then further polished using silica solution.TEM samples were obtained through further mechanicalthinning and ion thinning ofthe above specimens［24，25］.

2.2Characterization methods

The material properties and mechanical behaviors of the cross-section samples were measured at different spatial scales using experimental techniques including SEM，TEM，and MRS.

A Zeiss EVO/MA15 SEM system was used to measure the micro-structure of cross-section samples.The accelerating voltage ofthis system is 20 kVand its ultimate resolution is 3 nm.A JEM-2010 TEM system was applied to characterize the nanoscale morphology of the samples.The point resolution of this system is up to 0.23 nm，and its lattice resolution is 0.14 nm.

The Raman spectroscopy experiments in this work were carried out with a Renishaw InVia microscopic confocal Raman system.A UV laser with 325 nm wavelength，whose output was regulated to 5%，was used to analyze the surface of the ε-Si wafer.A 40×UV object lens（NA=0.50）was selected，giving an incident laser spot size of about 5 μm in diameter.

For the cross-section sample，spectral data from a 40 μm×20 μm region in the vicinity of the multilayers was obtained using Raman mapping（streamline）with 1.2 and 0.1 μm step lengths along the X and Y directions（viz.，parallel and vertical to the interfaces），respectively.During streamline measurement，the sampling spot of Raman laser was focused into a narrow line（not a circular）parallel to Y direction（vertical to the interface in this work）with about 1.2μmin thickness and 50μm in length.The data collection was first along this focus line with 1.2 μm step length.Then，the microscope stage moved along the X direction with a 0.1μmstep length，and the data collection wasrepeated.So，a 532 nm laser was used at 100%output power.A 50×object lens（NA=0.80）was selected，giving an incident laser spot size of about 1 μm in diameter.

3　Experimental results

3.1SEM and TEM results

虽然广玉兰普普通通，但作者却独具慧眼，写法与众不同。广玉兰四季常青，一般人们关注他的枝叶常绿，感受到其生机盎然，但作者偏偏被掩映在绿叶之间的大朵的花所吸引；一般人看花，会被其香味、颜色、质地所吸引，但作者却能感受到广玉兰的精神；一般人会着力描写盛开的花，但作者却能从花的次第开放，尤其是从凋谢的花中感受到她旺盛的生命力。作者的写作视角总是与常人不同，另辟蹊径，让读者对广玉兰认识耳目一新。教学中教师正是通过比较的方法，遵循作者写作之路上引导学生去关注表达，让文章写作模块深深烙在孩子心中。

Figure 2a shows an SEM image of a cross-section sample. The image is composed of several rectangular stripes distinguishable fromone anotherby theirdifferentgrayscales.The darkest stripe was the epoxy resin adhering the two（left and right）ε-Siwafers together.The region ofdeep grayscale atthe right side was the monocrystalline silicon（C-Si）substrate. The region next to C-Si，in which the grayscale changed gradually，was the graded germanium silicon buffer layer（GexSi1-x）.Finally，the bright area between the epoxy resin and GexSi1-xlayers，was the relaxed germanium silicon buffer layer（Ge0.2Si0.8）.The interface between the silicon substrate and the graded germanium silicon buffer layer was clear，straight，continuous，and complete.So wasthe interface between the two buffer layers，illustrating that a better transition between different layers was achieved in this strained silicon sample.The thicknesses of the graded and relaxed germanium silicon bufferlayerswere 2.7 and 0.9μm，respectively.The ε-Si was too thin to be observable by SEM.

Fig.2 a SEM.b HR-TEM images of a cross-section sample

Figure 2b shows a high resolution TEM（HR-TEM）image of a cross-section sample.The image clearly shows three different regions from right to left；the epoxy resin adhesive layer（the brightest region，where the pattern is totally disordered），the ε-Si layer，and the relaxed germanium sil-icon buffer layer，respectively.Both the ε-Si layer and the Ge0.2Si0.8layer were clean and flat without any visible defects/dislocations.Theε-Si/Ge0.2Si0.8interface was clear，straight，continuous，and complete.The left edge of the ε-Si layer，namely the surface of the ε-Si wafer，was flat at the atomic level.The thickness of the ε-Si layer was about 16.43 nm.Additionally，the lattice structure of the Ge0.2Si0.8layer was similar to that of the ε-Si layer，and it remained continuous atthe interface.Hence，the deformation and strain were continuous from the Ge0.2Si0.8layerto theε-Silayer.It can also be seen from Fig.2b thatthe crystalorientation ofthe cross-section sample was［110］，while the growth direction of the ε-Si layer was［001］.

3.2Raman experiments

A typical spectrum of the upper surface of the ε-Si wafer，which was achieved using a 325 nm laser，is shown in Fig.3a. The penetration depth of the 325 nm laser in the monocrystalline silicon is about 10 nm［26］，almost the same as the thickness oftheε-Silayer（Fig.2b）.Therefore，allthe Raman information in Fig.3a was derived from the strained silicon layer.The characteristic peak of the Si-Si band near 500 cm-1was single，strong，and narrow，indicating that the strained silicon prepared by RPCVDin thiswork wasprimarily in a monocrystalline state.Thisresultisin good agreement with those of the TEM shown in Fig.2b.

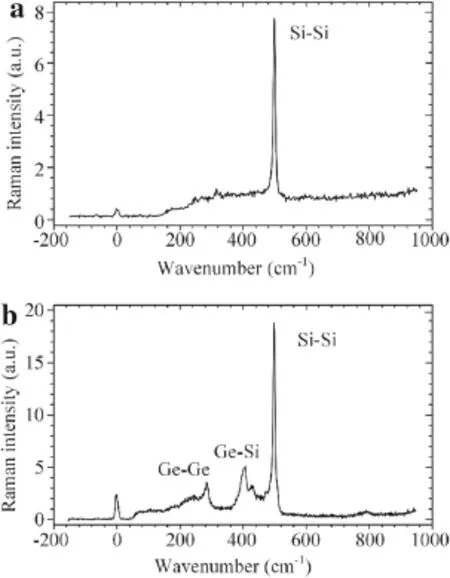
Fig.3 Raman spectra of a the surface of the ε-Si wafer using a 325 nm laser，and b the cross-section sample using a 532 nm laser

Fig.4（Color online）Measured wavenumber a mapping image and b distribution along the depth direction for the cross-section sample

Figure 3b shows a typical Raman spectrum of germanium silicon detected from the cross-section sample.Three typical peaks were observable in this spectrum:the Si-Si band around 500 cm-1，the Ge-Si band around 400 cm-1，and the Ge-Ge band around 300 cm-1，respectively.When the Sielementispredominantin Ge-Sialloy，such asin the buffer layers in this work，the Si-Si band is still strong and narrow enough for mechanical analysis.

Figure 4a shows the wavenumber image of the Si-Si peak obtained by Raman mapping on the cross-section sample in a 40 μm×20 μm region near the multilayer interfaces.The wavenumber distribution along the depth direction is shown in Fig.4b.The wavenumber of each sampling spot inside the C-Si substrate fluctuated slightly near 520 cm-1.Within the GexSi1-xlayer，it increased rapidly and almost linearly with depth.Itthen remained steady inside the relaxed bufferlayer. Raman information fromtheε-Silayerwashardly observable in the Raman spectra ofthe cross-section sample because the thickness of the ε-Si layer was about 10 nm，two orders of magnitude less than the spatial resolution（viz.，the size of sampling spot），about 1 μm，of the Raman system.

4　Raman-mechanical relationship of silicon-based semiconductor materials

Raman-mechanical measurements are based on deep understanding of the quantitative relationship between the Ramanshift and stress/strain of any given material.For the case of crystalline silicon，Eq.（1）gives a secular equation based on lattice dynamics for the Raman measurement of the［100］crystal orientation

where p，q，and r denote the components of the phonon deformation potential，εi（i=1-6）are the strain components，uk（k=1，2，3）are the atom displacement components，and direction footnotes 1，2，3 are regarded as normalto the crystallographic planes（100），（010），and（001），respectively，without loss of generality.

The shift△wjbetween the Raman wavenumber of an optical mode with strain，wj（j=1，2，3），and without strain，w0，can be calculated from the eigenvalues as follows

In the case of biaxial stress σ in the（001）plane，the stress tensor components σ1=σ2=σ and σ3=0.Using generalized Hooke’s law，

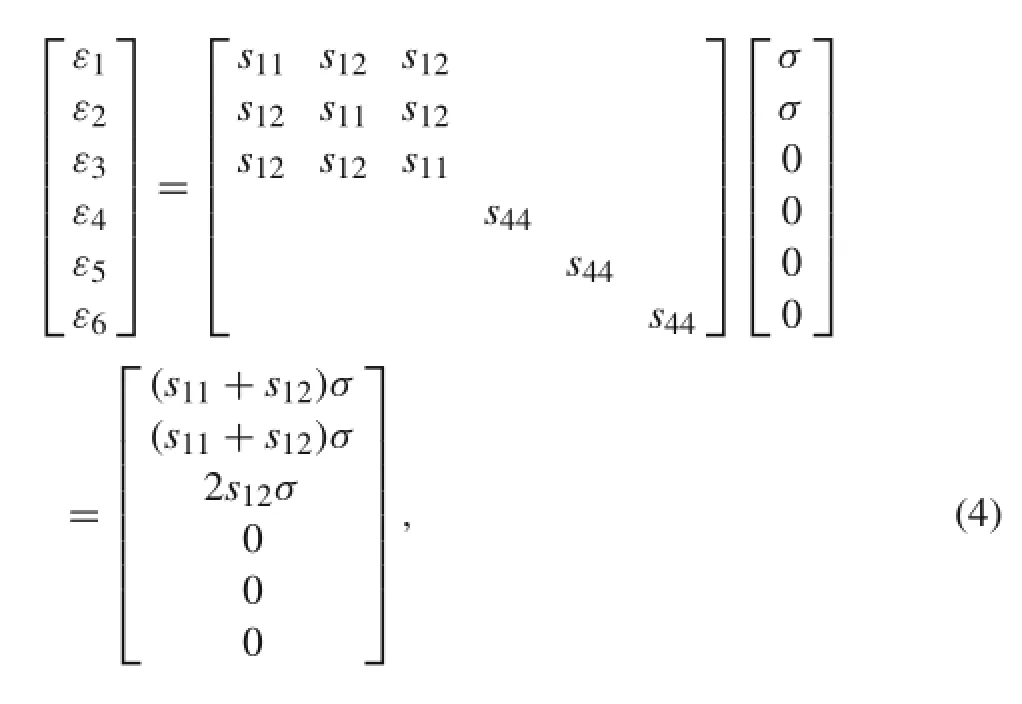
where s11，s12，and s44are the compliance coefficient components of monocrystalline silicon.

During the backscattering measurement of the（001）plane，only the third eigenvalue equation is Raman visible according to the Raman selection rules［27］.Hence， Eq.（3）becomes Eq.（5）in the biaxial stress state，where w0=520 cm-1，，s11= 7.68×10-12Pa-1，and s12=-2.14×10-12Pa-1.

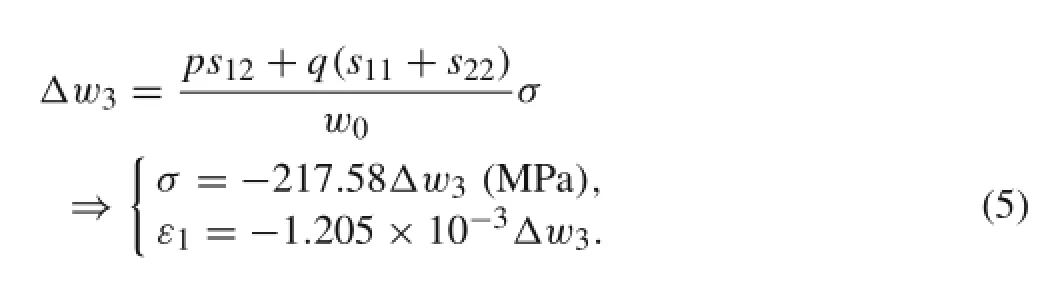
In the case of uniaxial stress（if σ1=σ，σ2=σ3=0），

The Raman-mechanical model above was not directly applicable in this work because the cross-section of the sample was in［110］crystal orientation，as shown in Fig.2b，for which the mechanicalparameters，phonon deformation properties，and Raman selection rules are all different from those in［100］crystal orientation.Therefore，it was essential to rebuild the Raman-mechanicalrelationship forresidualRaman measurements on［110］crystal orientation before any analysis of the Raman results in this work.

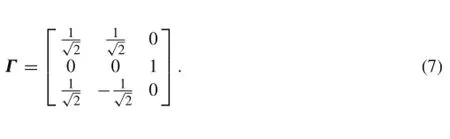
For the backscattering measurement of the cross-section sample，the coordinate transformation matrix Γ is given in Eq.（7）according to the coordinate set shown in Fig.1b.

Since the normal stress of the cross-section surface was totally released and the materialwas in a uniaxialstress state，the residualstress to be measured was parallelto the GeSi/CSi interface，（viz.，σX= σ，σY= σZ=0）.The strain components（εi，i=X，Y，Z），as wellas the components of the phonon deformation potential（Kjk，j，k=X，Y，Z），in the X-Y-Z coordinate set shown in Fig.1b can be obtained using coordinate transformation as follows

Substituting Eq.（8）into the secular equation based on lattice dynamics yields

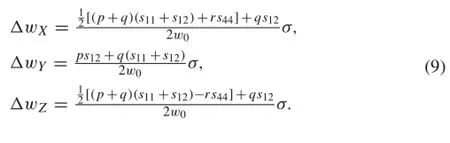
During backscattering measurementon the Z-plane，only the third eigenvalue equation is Raman visible according to the Raman selection rules.Hence，Eq.（9）becomes Eq.（10）for the analysis of residual stress in the cross-section sample in thiswork，and s44=1.26×10-11Pa-1.

For the Ge-Si alloy，the lattice dynamics equation is still applicable.Owing to the influence of phonon confinement［28］，the change in the wavenumber of the Si-Si band in the Raman spectrum of germanium silicon is not only induced by strain，butalso by phonon confinement.An empiricalrelationship was determined，by Tsang et al.［29］，between the Raman wavenumber wSi-Si，the Ge content x，and strainεfor［100］backscattering Raman measurements of Ge-Si alloy just by introducing a 62 x compensation for the wavenumber change to account for the influence of the phonon confinement.Meanwhile，the elastic parameters of germanium silicon follow the modulus-content linear model［7，30，31］

Therefore，the Raman-strain relationship of germanium silicon in the uniaxial stress state for the backscattering measurement of the［110］cross-section sample is as follows

5　Residual stress analyses

A Lorenz function was used to fit all the Raman spectra. The average wavenumber of standard silicon without stress is w0=519.78 cm-1.It was calibrated，on the same day as the above measurements，on an original silicon wafer similar to those used for the ε-Si samples in this work. The average wavenumberobtained by backscattering Raman measurement on the surface of the ε-Si wafer at 66 sampling spots was 511.98 cm-1.As described above，all the layers were epitaxially grown on（001）plane silicon wafers. Figure 2b shows the perfect monocrystalline lattice of the strained silicon layer.Therefore，Eq.（5）was applicable to evaluate the average strain of the strained silicon layer，ε= -1.205×10-3×（511.98-519.78）=9.40/00≈1%and the average residual stress σ=-217.5×（511.98-519.78）= 1.70 GPa.

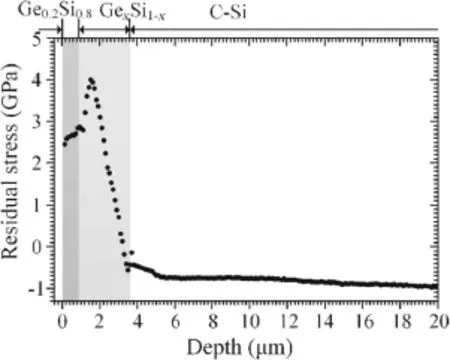
Fig.5 Distribution of residual stress in the cross-section sample

Forthe backscattering measurementson the cross-section，which had［110］crystal orientation，Eqs.（10）and（12）were applicable to evaluate the residual stress of sampling spots in the C-Si substrate and germanium silicon buffer layers，respectively.Hence，the residual stress distribution was obtained along the depth direction of this multi-layer structure as shown in Fig.5.

The experimental results in Fig.5 show that the residual stress was inhomogeneously distributed inside the material. In the C-Si substrate，the residual stress changed linearly with depth，which led to a unitary warping of the whole ε-Si wafer.The residual stress then changed dramatically inside the graded germanium silicon buffer layer.In detail，from the GexSi1-x/Si interface to the Ge0.2Si0.8/GexSi1-xinterface，the residual stress increased rapidly and almost linearly，reached a maximum，and then decreased slightly. This occurred because intrinsic residual stress is generally induced by lattice mismatch.With increasing Ge content in the GexSi1-xbuffer layer，the average size of the lattice structure was enlarged，accompanied by increased lattice mismatches.Because lattice size cannot be enlarged continuously，it reached a stable and saturated state inside the GexSi1-xbufferlayer.Afterthat，furtherincreasesin Ge contentwere only helpfulforthe gradualrelaxation oralleviation of the lattice mismatch，releasing the intrinsic residual stress until it was close to the Ge0.2Si0.8/GexSi1-xinterface.In the relaxed germanium silicon buffer layer，the lattice structure was steady，and；hence，the residual stress was stabilized. Near the ε-Si/Ge0.2Si0.8interface，it was about 2.45 GPa.

Fig.6 Flow chartofthe measurementofresidualstressin a multi-layer semiconductor heterostructure

6　Conclusion

Taking ε-Si/Ge0.2Si0.8/GexSi1-x/C-Si（shown in Fig.1）as an example of multi-layer heterostructure，this paper has presented a methodological study of residual stress measurement（Fig.6）.For such multi-layer semiconductor heterostructures，it is efficient to prepare cross-section samples and then investigate theirmaterialand mechanicalproperties. SEM and TEM can be used to measure the geometric parametersofthe multilayerstructure，while MRS，TEM，perhaps energy dispersive spectroscopy（EDS），and others are powerful techniques for characterizing material composition and properties.Coincident with these experimental works，the Raman to stress/strain relationship ofthe studied materialfor a specific crystalorientation should be investigated at a theoretical level.Finally，the distribution of residual stress along the depth ofthe multi-layerheterostructure can be determined by combining the experimental and theoretical results.The geometric and material properties measured by SEM，TEM，MRS，and EDS experiments（such as those shown in Figs.2-4）are all essential parameters for calculation of the Raman to stress/strain relationship（such as by Eqs.（10）and（12））to evaluate the residual stress and its distribution（such as that shown in Fig.5）.

Acknowledgments The project was supported by the National Basic Research Program of China（Grant 2012CB937500），the National Natural Science Foundation of China（Grants 11422219，11227202，11372217，11272232），the Program for New Century Excellent Talents in University（Grant NCET-13），and China Scholarship Council（201308120092）.

1.Jacobsen，R.S.，Andersen，K.N.，Borel，P.I.，et al.:Strained silicon as a new electro-optic material.Nature 441，199-202（2006）

2.Zhou，Z.W.，He，J.K.，Wang，R.C.:Heteroepitaxial growth of Ge films on Si substrates and its applications in optoelectronics. Physics 40，799-806（2011）

3.Gogotsi，Y.，Baek，C.，Kirscht，F.:Raman microspectroscopy study of processing-induced phase transformations and residual stress in silicon.Semicond.Sci.Technol.14，936-944（1999）

4.Zhang，Q.C.，Jiang，Z.Y.，Jiang，H.F.，etal.:On the propagation and pulsation of Portevin-Le Chatelier deformation bands:an experimental study with digital speckle pattern metrology.Int.J.Plast. 21，2150-2173（2005）

5.Jiang，H.F.，Zhang，Q.C.，Chen，X.D.，et al.:Three types of Portevin-Le Chatelier effects:experiment and modelling.Acta Mater.55，2219-2228（2007）

6.Wang，M.，Hu，X.F.，Wu，X.P.:Internal microstructure evolution of aluminum foams under compression.Mater.Res.Bull.41，1949-1958（2006）

7.Kasper，E.:PropertiesofStrained and Relaxed Silicon Germanium. INSPEC，Institution of Electrical Engineers，London（1995）

8.Janssen，G.C.A.M.，Abdalla，M.M.，Keulen，V.F.，etal.:Celebrating the 100th anniversary of the Stoney equation for film stress:developments from polycrystalline steel strips to single crystal silicon wafers.Thin Solid Films 517，1858-1867（2009）

9.Doyle，S.，Chernenko，V.A.，Besseghini，S.，etal.:Residualstressin Ni-Mn-Ga thin films deposited on different substrates.Eur.Phys. J.Spec.Top.158，99-105（2008）

10.Pan，X.，Tan，C.W.，Miao，J.，etal.:The stress analysis of SiMEMS devices by micro-Raman technique.Thin Solid Films 517，4905-4908（2009）

11.Li，X.D.，Tao，G.，Yang，Y.Z.:Continual deformation analysis with scanning phase method and time sequence phase method in temporal speckle pattern interferometry.Opt.Laser Technol.33，53-59（2001）

12.Zhang，Z.F.，Kang，Y.L.，Wang，H.W.，et al.:A novel coarse-fine search scheme for digital image correlation method.Measurement 39，710-718（2006）

13.Jiang，L.B.，Guo，B.Q.，Xie，H.M.:Identification ofthe elastic stiffnessofcompositesusing the virtualfieldsmethod and digitalimage correlation.Acta Mech.Sin.31，173-180（2015）

14.Stoney，G.G.:The tension of metallic films deposited by electrolysis.Proc.R.Soc.Lond.A 82，172-175（1909）

15.Qiu，W.，Kang，Y.L.，Lei，Z.K.，et al.:Experimental study of the Raman strain rosette based on the carbon nanotube strain sensor. J.Raman Spectrosc.41，1216-1220（2010）

16.Qiu，W.，Li，Q.，Lei，Z.K.，et al.:The use of a carbon nanotube sensorformeasuring strain by micro-Raman spectroscopy.Carbon 53，161-168（2013）

17.Qiu，W.，Kang，Y.L.:Mechanical behaviour study of microdevice and nanomaterials by Raman spectroscopy.Chin.Sci.Bull.59，2811-2824（2014）

18.De Wolf，I.:Micro-Raman spectroscopy to study local mechanical stress in silicon integrated circuits.Semicond.Sci.Technol.11，139-154（1996）

19.Hayazawa，N.，Motohashi，M.，Saito，Y.，et al.:Visualization of localized strain of a crystalline thin layer at the nanoscale by tip-enhanced Raman spectroscopy and microscopy.J.Raman Spectrosc.38，684-696（2007）

20.Li，Q.，Qiu，W.，Tan，H.，et al.:Micro-Raman spectroscopy stress measurement method for porous silicon film.Opt.Lasers Eng.48，1119-1125（2010）

21.Kang，Y.L.，Qiu，Y.，Lei，Z.K.，etal.:An application ofRaman spectroscopy on the measurement of residual stress in porous silicon. Opt.Lasers Eng.43，847-855（2005）

22.Qiu，W.，Kang，Y.L.，Li，Q.，et al.:Experimental analysis for the effect of dynamic capillarity on stress transformation in porous silicon.Appl.Phys.Lett.92，041906（2008）

23.Liang，R.R.，Zhang，K.，Yang，Z.R.，et al.:Fabrication and characterization of strained Si material using SiGe virtual substrate for high mobility devices.Chin.J.Semicond.28，1518-1522（2007）

24.Zhao，C.W.，Xing，Y.M.，Zhou，C.E.，etal.:Experimentalexamination of displacement and strain fields in an edge dislocation core. Acta Mater.56，2570-2575（2008）

25.She，X.，Wang，H.:Thermal stability of ALD lanthanum aluminate thin films on Si（100）.J.Mater.Sci.Technol.30，347-352（2014）

26.Moutanabbir，O.，Reiche，M.，Hähnel，A.，et al.:Multiwavelength micro-Raman analysis of strain in nanopatterned ultrathin strained silicon-on-insulator.Appl.Phys.Lett.97，053105（2010）

27.Wolf，I.D.，Maes，H.，Jones，S.K.:Stress measurements in silicon devices through Raman spectroscopy:bridging the gap between theory and experiment.Appl.Phys.79，7148-7156（1996）

28.Alonso，M.I.，Winer，K.:Raman spectra of c-Si1-x Ge x alloys. Phys.Rev.B 39，10056-10062（1989）

29.Tsang，J.C.，Mooney，P.M.，Dacol，F.，etal.:Measurementsofalloy composition and strain in thin GexSi1-xlayers.Appl.Phys.75，8098-8108（1994）

30.Dismukes，J.P.，Ekstrom，L.，Paff，R.J.:Lattice parameter and density in germanium-silicon alloys.J.Phys.Chem.68，3021-3027（1964）

31.Landolt，H.，Börnstein，R.:Numerical data and functional relationships in science and technology new series，Group III，vol.17a. Springer，Berlin（1982）

29 September 2015/Revised:17 November 2015/Accepted:8 December 2015/Published online:12 July 2016

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics，Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016