Gradient systems and mechanical systems
Fengxiang Mei·Huibin Wu
RESEARCH PAPER
Gradient systems and mechanical systems
Fengxiang Mei1·Huibin Wu2
All types of gradient systems and their properties are discussed.Two problems connected with gradient systems and mechanical systems are studied.One is the direct problem of transforming a mechanical system into a gradient system,and the other is the inverse problem,which is transforming a gradient system into a mechanical system. Keywords Gradient system·Mechanical system·Stability
1 Introduction
Hirsch and Smale[1]indicates that the Lyapunov function is especially suitable for studying the gradient system. McLachlan et al.[2]points out that in addition to the general gradient system,there is the skew-gradient system,the gradient system with a symmetric negative definite matrix,and the gradientsystem with a negative semi-definite matrix. Some results have been obtained in the research of the relation between constrained mechanical systems and gradient[3-15].Firstly,in this paper,the above four types of basic gradient systems will be generalized to the combined situations and the cases whose matrix and function contain time t. Secondly,the constrained mechanical system will be transformed into a gradientsystemundercertain condition,and its integration and stability will be discussed by using the properties of gradient system.Finally,the gradient system willbe transformed into a mechanical system,and its integration and stability will be studied.
✉ Huibin Wu huibinwu@bit.edu.cn
1School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China
2School of Mathematics,Beijing Institute of Technology,Beijing 100081,China
2 Gradient systems
Gradient systems can be divided into four types:basic type,combined type,generalized type I,and generalized type II.
2.1Basic types
(1)General gradient system The differential equations are as follows[1,2]

which have the following properties:forall x,if and only if x is an equilibrium of system(1);at an equilibrium of system(1),the eigenvalues are real.
(2)Skew-gradient system The differential equations are as follows[2]

They have the following properties:is an integral.
(3)Gradient system with a symmetric negative definite matrix The differential equations are as follows[2]

(4)Gradient system with a negative semi-definite matrix The differential equations are as follows[2]

2.2Combined types
By using the above four basic types,we can obtain the following six combined gradient systems:
(1)Combined type I
The differential equations are

The matrices of combined gradient systems(6),(7),and(10)are symmetric negative definite,and those ofsystems(5) and(8)are negative definite.This is conducive to the study of stability.
The above 10 gradient systems can be used to discuss the stability of time-independent mechanical systems.
2.3Generalized type I
Extending the function V of the above 10 gradient systems to the cases of containing time t gives the following 10 categories:


2.4Generalized type II

3 Direct problems
The direct problem is to transform a constrained mechanical system into a gradient system under certain conditions. Some examples of a holonomic system with a single degree of freedom are as follows.
Example 1 A single degree of freedom system is
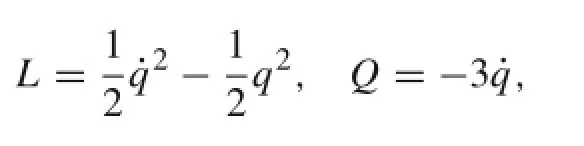
whose differential equation is
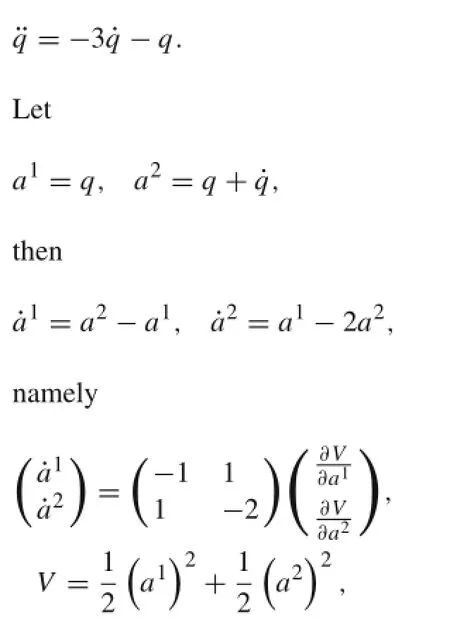
which is a gradient system of type Eq.(3).The zero solution a1=a2=0 is asymptotically stable.Itcan also be rewritten as
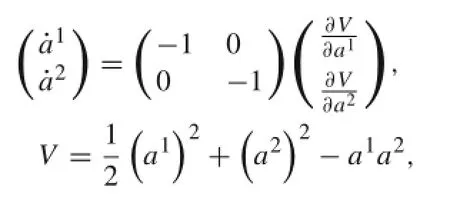
which isa gradientsystemoftype Eq.(1)whose zero solution a1=a2=0 is asymptotically stable.

The differential equation is
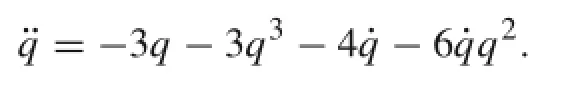

which is a combined gradient system of type Eq.(7)whose zero solution a1=a2=0 is asymptotically stable.

which is a gradient system of type Eq.(12)whose zero solution a1=a2=0 is stable.
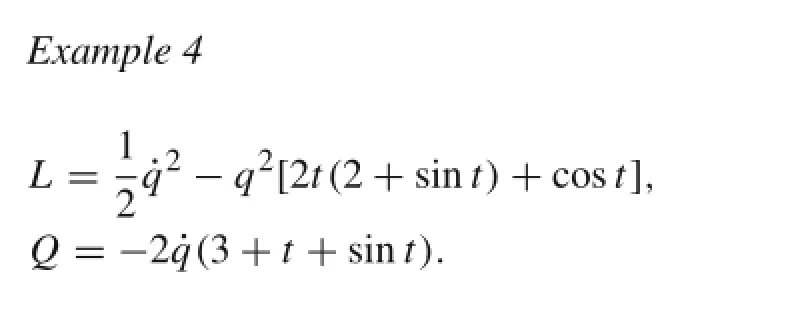

which is a gradient system of type Eq.(22)whose zero solution a1=a2=0 is asymptotically stable.
4 Inverse problems
The inverse problem is to transform a gradient system into a constrained mechanical system under certain conditions. Now we discuss the inverse problems of examples 1-4.
Example 5 A gradient system is
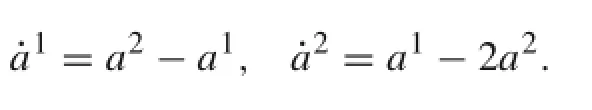
Try to transform it into a constrained mechanical system.
Taking derivative with respect to time t for the above first equation and using the second equation,we obtain

then the gradientsystemcan be transformed into a holonomic system:

Rewrite the gradient system as the following form
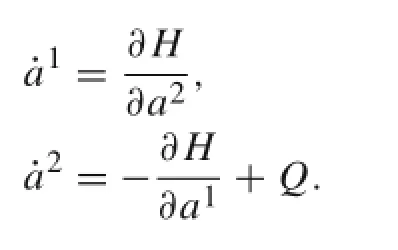
Then it can become a Hamilton system with an added term,in which
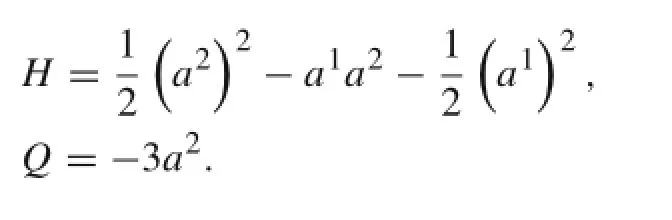
Also,this can be transformed into a generalized Birkhoff system:

Example 6 A gradient system is

Try to transform it into a constrained mechanical system.
Taking the derivative with respect to time t for the above second equation and using the first equation,we get

which can be transformed into a holonomic system:

Also,it can be transformed into a Hamilton system with an added term:

or a generalized Birkhoff system:

Example 7 A gradient system is
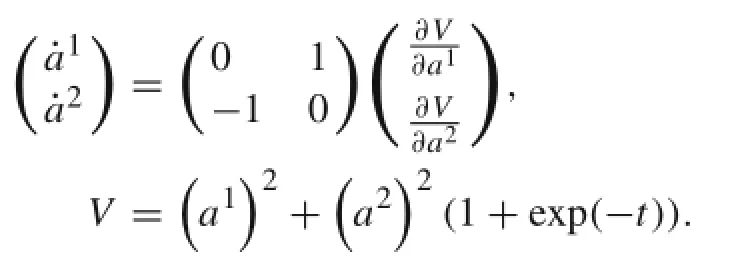
Try to transform it into a constrained mechanical system. The differential equations are as

Differentiating the above first equation with respect to t and using the second equation,we have

which can be transformed into a holonomic system:

Also,it can be rewritten as a Hamilton system:

or a Birkhoff system:

Example 8 A gradient system is as

Try to transform it into a constrained mechanical system.
The differential equations are as

Differentiating the above first equation with respect to t,using the second equation and letting
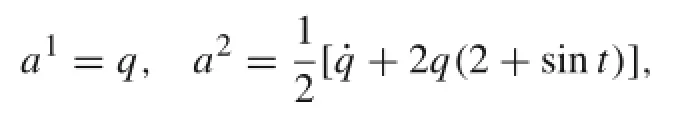
we obtain

This can be transformed into a holonomic system:

or a Hamilton system with an added term:
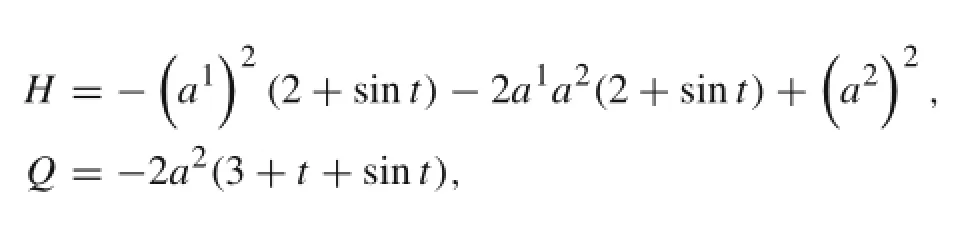
or a generalized Birkhoff system:

5 Conclusions
The gradient system is a type of mathematical system that is very convenient for the studies of integration and stability of solutions.If a mechanical system can be transformed into a gradient system,one can discuss the integration and stability of solutions of the system by using the property of a gradientsystem.Forexample,time-independentLagrange system,time-independent Hamilton systems,and autonomous Birkhoff systems are all skew-gradient systems.Therefore,the Hamiltonian H or Birkhoffian B is an integral of the system. Also,if H or B can become a Lyapunov function,then the solution is stable.Extending the gradient system to the case whose matrix orfunction contains time t,one can discuss the stability of time-dependent mechanical system with the help of such a gradient system.
Acknowledgments The projectwas supported by the NationalNatural Science Foundation of China(Grant 11272050).
1.Hirsch,M.W.,Smale,S.:Differential Equations,Dynamical Systems,and Linear Algebra.Academic Press,New York(1974)
2.McLachlan,R.I.,Quispel,G.R.W.,Robidoux,N.:Geometric integration using discrete gradients.Philos.Trans.R.Soc.Lond.A 357,1021-1045(1999)
3.Mei,F.X.:On gradient systems.Mech.Eng.34,89-90(2012)(in Chinese)
4.Mei,F.X.,Wu,H.B.:A gradient representation for generalized Birkhoff system.J.Dyn.Control 10,289-292(2012)(in Chinese)
5.Mei,F.X.,Cui,J.C.,Wu,H.B.:A gradient representation and a fractional gradient representation of Birkhoff system.Trans.Beijing Inst.Technol.32,1298-1300(2012)(in Chinese)
6.Lou,Z.M.,Mei,F.X.:A second order gradient representation of mechanics system.Acta Phys.Sin.61,024502(2012)(in Chinese)
7.Mei,F.X.,Wu,H.B.:Generalized Hamilton system and gradient system.Sci.Sin.-Phys.Mech.Astron.43,538-540(2013)(in Chinese)
8.Chen,X.W.,Zhao,G.L.,Mei,F.X.:A fractional gradient representation of the Poincaré equations.Nonlinear Dyn.73,579-582(2013)
9.Mei,F.X.:On skew-gradientsystems.Mech.Eng.35,79-81(2013)(in Chinese)
10.Mei,F.X.:Analytical Mechanics(II).Beijing Institute of Technology Press,Beijing(2013)(in Chinese)
11.Mei,F.X.,Wu,H.B.:A gradient representation of first-order Lagrange system.Acta Phys.Sin.62,214501(2013)(in Chinese)
12.Mei,F.X.,Wu,H.B.:Generalized Birkhoff system and a kind of combined gradient system.Acta Phys.Sin.64,184501(2015)(in Chinese)
13.Wu,H.B.,Mei,F.X.:A gradient representation of holonomic system in the event space.Acta Phys.Sin.64,234501(2015)(in Chinese)
14.Mei,F.X.,Wu,H.B.:Skew-gradient representation of generalized Birkhoffian system.Chin.Phys.B 24,104502(2015)
15.Mei,F.X.,Wu,H.B.:Two kindsofgeneralized gradientrepresentations forholonomic mechanicalsystems.Chin.Phys.B 25,014502(2016)
29 August 2015/Revised:26 February 2016/Accepted:27 April 2016/Published online:2 September 2016
©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016
- Acta Mechanica Sinica的其它文章
- Entropic force between biomembranes
- Numerical analysis of stress distribution in the upper arm tissues under an inflatable cuff:Implications for noninvasive blood pressure measurement
- A direct probabilistic approach to solve state equations for nonlinear systems under random excitation
- Nonlinear integral resonant controller for vibration reduction in nonlinear systems
- Reliability assessment on interfacial failure of thermal barrier coatings
- Numerical study on the deformation of soil stratum and vertical wells with gas hydrate dissociation

