Numerical analysis of stress distribution in the upper arm tissues under an inflatable cuff:Implications for noninvasive blood pressure measurement

Zhipeng Deng·Fuyou Liang，2



RESEARCH PAPER

Numerical analysis of stress distribution in the upper arm tissues under an inflatable cuff:Implications for noninvasive blood pressure measurement

Zhipeng Deng1·Fuyou Liang1，2

An inflatable cuff wrapped around the upper arm is widely used in noninvasive blood pressure measurement. However，the mechanical interaction between cuff and arm tissues，a factor that potentially affects the accuracy of noninvasive blood pressure measurement，remains rarely addressed.In the present study，finite element（FE）models were constructed to quantify intra-arm stresses generated by cuffcompression，aiming to provide some theoreticalevidence foridentifying factors ofimportance forblood pressure measurement or explaining clinical observations.Obtained results showed that the simulated tissue stresses were highly sensitive to the distribution of cuff pressure on the arm surface and the contact condition between muscle and bone.In contrast，the magnitude of cuff pressure and small variations in elastic properties of arm soft tissues had little influence on the efficiency of pressure transmission in arm tissues.In particular，it was found that a thickened subcutaneous fat layer in obese subjects significantly reduced the effective pressure transmitted to the brachial artery，which may explain why blood pressure overestimation occurs more frequently in obese subjects in noninvasive blood pressure measurement.

Noninvasive blood pressure measurement· Inflatable cuff·Upper arm·Finite element（FE）model· Loading and contact conditions·Stress distribution·Obese patients

✉ Fuyou Liang fuyouliang@sjtu.edu.cn

1School of Naval Architecture，Ocean&Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

2Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration（CISSE），Shanghai 200240，China

1　Introduction

Arterial blood pressures have long been recognized as an important predictive factor for cardiovascular events［1，2］. Noninvasive evaluation of arterial blood pressures can be traced back to over a century ago［3，4］and is nowadays a routine practice in clinical settings.In recent years，the appearance of automatic blood pressure measurement devices hasenabled the increasing application ofhome-based blood pressure monitoring［5，6］.Existing techniquesfornoninvasive blood pressure measurementcan be categorized into two major families according to the mechanisms underlying pressure estimation，namely，the auscultatory（orRiva-Rocci）technique and the oscillometric technique.The auscultatory technique is based on the detection of the Korotkoff sounds generated by flow turbulences accompanying the collapsing of an artery under an external load，whereas，the oscillometric technique utilizes pressure oscillation waves detected in a cuff［7，8］.Both techniques，though differing in working principle，need an inflatable cuff wrapped around the extremity（usually the upperarmorthe wrist），which imposes a varying externalforce on the under-cuffarteriestotriggerbiomechanical signals that can be noninvasively detected and exploited for blood pressure estimation.

Despite the well-established mechanisms forand the wide application of noninvasive blood pressure measurement，the accuracy of measurement yet remains an issue of frequent discussion［9］.Multiple factors have been found to affect the accuracy of blood pressure measurement，including cuff parameters（e.g.，width and length of cuff）［10］，biomechanical properties（e.g.，elastic properties of brachial arterial walls）［11］，and hemodynamic status of the cardiovascular system（e.g.，mean arterial pressure，pulse pressure）［12］. Previous studies dedicated to this subject often employed asimplified theoretical model to account for the mechanical interaction between cuff and under-cuff soft tissues［11，12］. Simplified models，however，lack the ability to fully explain the effects of the geometrical and mechanical properties of under-cuff soft tissues on blood pressure measurement. Theoretically，stress distribution in under-cuff soft tissues is an important determinant of the deformation of undercuff arteries and the characteristics of signals detected on the skin surface or in the cuff.In this sense，a thorough investigation of the mechanical response of soft tissues to cuff pressurization may provide useful knowledge for identifying factors of importance for noninvasive blood pressure measurement.The issue has been partly addressed in a few studies［13，14］.For instance，Cristalli and Ursino［13］analyzed the distribution of stress and strain in an idealized arm segment using a finite element（FE）model.They found that transmission of cuff pressure across arm tissues was significantly affected by the mechanical properties of arm tissues. Then Lan et al.［14］took the study a step further by constructing an FE model of the upper arm embedded with a brachial artery.Their study revealed that the compressibility rather than the stiffness of arm tissues significantly affected the transmission of pressure from the cuff to the outer wall of the brachial artery.These studies demonstrated the potential value of computational models in quantifying the interaction between cuff and arm tissues.In contrast to numerical analysis，high-precision in vivo measurement of tissue stresses in a living human body has been difficult due to technical limitations and ethical considerations.As an alternative，measurements could be performed on human cadavers in a relatively easier way.For example，Hargens et al.［15，16］measured the distribution of tissue fluid pressure in human upper arms and thighs beneath a pneumatic tourniquet（a device similar to the cuff used for blood pressure measurement）by inserting steel catheters into fresh human cadavers.Their experiments revealed the existence of a considerable damping effect when cuff pressure is transmitted from the arm surface toward the bone.The numerical results reported in Ref.［14］，however，showed that tissue pressure increased gradually from the arm surface to the bone. Given the limited agreements between reported numerical results and experimental data，constructing a computational model capable of reproducing available experimental data remains an essential step to uncovering the factors that dominate the mechanical interaction between cuff and arm tissues.

In the present study，we first carried out a series of numerical experiments based on an FE model of the upper arm coupled with an inflatable cuff so as to determine the model setup that permits reasonable predictions of experimental data.The model was then applied to investigate the effects of cuff loading conditions and the mechanical properties of arm soft tissues on the efficiency of pressure transmission from the cuff to the brachial artery.Moreover，we studied the effects of increased thickness of the subcutaneous fat layer on intra-arm pressure transmission，aiming to provide theoretical evidence for explaining the clinical observation that overestimation of blood pressures occurs frequently in obese patients［17］.

2　Materials and methods

2.1Construction of geometric models

Fig.1 Mesh models of the upper arm.a Cylinder-shaped ideal model. b Anatomic model（reconstructed from CT images）.c Moderate obese model（coated with a subcutaneous fat layer of 10 mm in thickness）. d Severe obese model（coated with a subcutaneous fatlayerof20 mm in thickness）.Aregionally amplified figure isadded to panel c to highlight the high-density meshes generated for the brachial artery

Two geometric modelswere firstbuiltfornumericalanalysis，one is a cylinder-shaped ideal model（Fig.1a），and the other is an anatomic model reconstructed from computed tomography（CT）images of a upper arm segment（Fig.1b）.The geometrical parameters of the ideal model were set in line with those used in previous studies［14］so thatourresultscan be compared with the existing ones.The length of the ideal upperarmmodelwas 260 mm，with the radiiofupperarmand bone being 52 and 12 mm，respectively.The brachial artery wasassumed to have a constantinternalradius（=2.5 mm）and wall thickness（=0.6 mm）along its axis，and was embedded in the arm tissue with a depth of 10 mm from the arm surface.To construct the anatomic model，CT images（obtained by cross-sectional scanning of the upper arm in interval of 2 mm along the axial direction）were first processed using a program written in Wolfram language（compiled in Mathematica 10.0，Wolfram Research，Inc.，USA）to extract the contours ofdifferenttissues，and then the data were imported into SolidWorks（SolidWorks 2014，Dassault Systems S.A，FRA）to reconstruct a three-dimensional（3-D）geometricmodel using a macro-instruction and lofting function.The geometricalparameters ofthe reconstructed anatomic model were comparable to those of the ideal model，although the radiiofarm，bone，and brachialarteriesvary in the axialdirection.It is noted that soft tissues like skin，fat，muscles，and connective tissues have been amalgamated as a unique soft tissue component（herein termed as muscle component）during modelconstruction because these tissues exhibitirregular connectionstoeach other，which willincrease the difficulty of modelreconstruction and prescription ofcomputation conditions.The simplification was expected to have little influence on the present analysis since muscles occupy the largest portion（over 80%in volume）of arm soft tissues in normal subjects.As a consequence，each arm model consisted of three components that represent the soft tissue，brachial artery，and bone，respectively.In obese patients，however，the subcutaneous fat layer is much thicker than in normal subjects，which may considerably affect stress distribution in arm tissues.Therefore，the anatomic model was further modified to simulate obese arms by adding a subcutaneous fat layer around the outer surface of the arm.Herein，the thickness of the subcutaneous fat layer was set respectively to be 10 and 20 mm to represent different degrees of obesity（Fig.1c，d）.

2.2Generation of computational meshes

The geometric models were imported into ANSYS（ANSYS 15.0，ANSYS Inc，USA）to generate computational meshes（see Fig.1）.In consideration of the small diameter of the brachial artery relative to the arm，mesh refinement was performed in the near artery regions（see Fig.1c）.The ideal and regular anatomic models（herein，the regular anatomic model refers to the model reconstructed from the CT images without adding a subcutaneous fat layer）contained 1356057 and 2304114 elements，respectively.Numerical experiments performed under a static loading condition proved thatfurtherincreasing the density ofmeshesgave less than 1%change in computed maximum principle stresses on the bone surface.

2.3Material properties

The upper arm consists of multiple tissues featuring anisotropic mechanicalproperties.The mostpronounced differences in mechanical properties exist among fat，muscles，bone，and the brachial arterial wall.For regular models，the subcutaneous fat layer was thin and，hence，was ignored；whereas，for obese models，the subcutaneous fat layer was separately modeled.From in vitro experiments，the mechanical properties of most biomaterials exhibited significant dependence on loading conditions［18，19］and for these materials hyperelastic models enabled a reasonable fitting of model predictions to experimental data［20-22］.In the present study，the Neo-Hookean hyperelastic model was used to represent the nonlinear elastic properties of the soft tissues.Arm soft tissues are slightly compressible with a Poisson’s ratio of 0.45 to 0.49［14］.Herein，the Poisson’s ratio was set to be 0.45.The strain-energy density function（Ψ）of the Neo-Hookean model can be expressed as［19］

By definition，the principalcomponents（σi）ofthe Cauchy stress can be derived from the strain-energy density function by

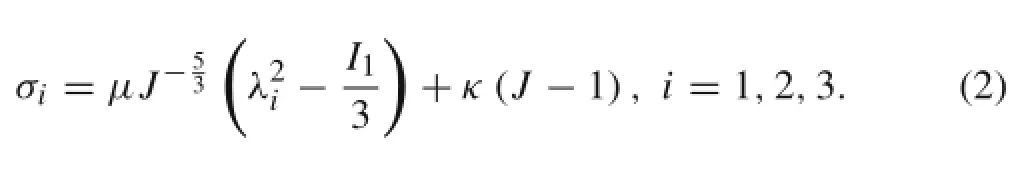
Because the mechanical properties differ among muscle，brachial artery wall，and fat，the parameters（μ，κ）of the Neo-Hookean model corresponding to each soft tissue should be determined separately.The mechanical properties of muscle，brachial artery wall，and fat are derivable from previous experimental studies［23-26］.Since experimental results were usually reported in form of discrete data points with potential data jumps，they cannot be used directly to estimate the parameters of the Neo-Hookean model.Herein，the experimental data were first fitted using nonlinear functions（see Fig.2）.It is noted that the experimental data of muscle reported in the literature exhibited considerable discrepancies，probably due to the differences in muscle tissues being tested or methods employed to measure stress and strain.For this reason，the experimental data from two studies［24，25］have been used to perform curve fitting.The fitted stress-strain relationships were then represented by the Neo-Hookean hyperelastic model through an internal parameter optimization algorithm in ANSYS，with the resulting model parameters being reported in Table 1. For the bone，a rigid model was adopted since its deformation is negligible compared with the soft tissues（a bone’s Young’s modulus is about 100 times larger than those of the soft tissues［14，20］）.

2.4Loading，contact and boundary conditions

Fig.2（Color online）Stress-strain relationships of arm soft tissues（including muscle，brachial artery wall，and fat）.Herein，the discrete experimental data were fitted by polynomial functions to facilitate the incorporation of experimental data in the computer models.The fitted curves were represented by the Neo-Hookean hyperelastic model through an internal parameter optimization algorithm in ANSYS，with the resulting model parameters being reported in Table 1

Table 1 Parametersofthe Neo-Hookean hyperelastic model.The parameters were estimated respectively for muscle，biracial artery wall，and fat based on the experimental data

Loading，contact，and boundary conditions of the models were prescribed on the basis of a careful analysis of the anatomicaland mechanicalproperties ofthe arm tissues.The main points related to the prescription ofthese conditions are summarized as follows

（1）Loading conditions:The width of the cuff was initially set to be 8 cm according to previous experimental conditions to allow a direct comparison of simulated results with the experimentaldata［15，16］.The cuffwas assumed to adhere to the outersurface ofthe upperarm. Based on thatassumption，the cuffmodelcan be simplified as a pressure loading condition applied to the outer surface of the arm.Pressures imposed on the arm outer surface by the cuff are not uniformly distributed in the axial direction due to the presence of a force gradient from the center to the edges of the cuff.According to the pressures measured in subcutaneous tissues under a cuff［15］，a distribution function was applied along the axial direction（see Fig.3b），where the pressure is equal to cuff bladder pressure at the location right beneath the center of the cuff and decreases gradually towards the proximal and distal edges of the cuff.In the circumferential direction，a uniform pressure distribution was assumed.The width of the cuff was later increased to 16 cm to simulate the situation of blood pressure measurement（the width of a regular adult cuff is 16 cm according to American Heart Association recommendations for cuff size［8］）.In this case，the axial distribution of cuff pressure was obtained by stretching the experimental data of the 8 cm cuff along the axial direction（see Fig.3c，d）.

（2）Contact conditions:a）Bonded contact conditions（no relative movement and closing and opening of contact surface permitted）were applied among the outer wall of the brachial artery，the fat，and the muscle；b）Rough contact conditions（no relative movement permitted，butallow closing and opening ofcontactsurface）were applied between the muscle and the bone. The rough contact conditions were prescribed based on the anatomical configuration of the upper arm muscle and bone.For instance，muscle fibers are embraced by the sarcolemma membrane，which is connected to the bone via connective tissues rather than being fixed directly on the bone［27，28］.Therefore，the contactconditionsshould permitdetachmentofthe muscle fromthe bone under certain conditions.As will be demonstrated later，fixing the muscle on the bone surface led to an incorrect prediction of pressure distribution in the arm tissues.

（3）Boundary conditions:the proximal and distal ends of the arm segment and the internal wall of the brachial artery were assumed to be stress free.

2.5Numerical methods

The deformation ofarmtissues wasgoverned by a static equilibriumequation.The equation wasdiscretized，togetherwith the loading and boundary conditions，in the computational domain based on FEs，forming a matrix equation system that relates displacements to loads

where K is the stiffness matrix，u is the displacement matrix，and D is the load matrix.

The system of Eq.（3）was solved in ANSYS using the preconditioned conjugate gradient（PCG）Solver.The PCG solver employs an iterative algorithm to solve sparse matrix systems and a parallel algorithm to improve the efficiency of computation.Once the solution converged，derivatives of strain and stress were calculated.

2.6Derivation of hydrostatic pressure in tissues

Fig.3 Distribution of cuff pressure along the axial direction of the arm surface.a Uniform distribution applied to the ideal arm model（8 cm cuff）. b Non-uniform distribution applied to the ideal arm model（8 cm cuff）.c Non-uniform distribution applied to the anatomic arm model（16 cm cuff）.d Plots of cuff pressures imposed on the arm surface as a function of the distance from the center of the cuff（the cuff pressures have been normalized by the cuff bladder pressure）.The non-uniform pressure distribution data for the 8 cm cuff have been adopted from Ref.［15］，whereas，those for the 16 cm cuff were obtained by stretching the data of the 8 cm cuff along the axial direction

The cuff affects the deformation of the brachial artery by imposing an external pressure on the outer wall of the artery.Therefore，the distribution of hydrostatic pressure in arm tissues is of major interest in the context of blood pressure measurement.In addition，since hydrostatic pressures in under-cuff arm segments have been measured in previous experimental studies［15，16］，evaluation of hydrostatic pressures would favor comparisons of numerical results with experimental data.In our numerical analysis，hydrostatic pressure was not explicitly solved，which has herein been calculated from stress variables using a user-defined function.For slightly compressible hyperelastic materials，hydrostatic pressure（p）can be estimated from stresses as

Here，σ1，σ2，and σ3stand for the principal stresses.

2.7Computation conditions

Three sets of computations were carried out.In the first set，the effects of cuff pressure distribution on arm surface and the contact condition between muscle and bone were investigated.In the second set，intra-arm stress distribution was computed using the anatomic model，with emphasis on addressing the effects of cuff pressure and the elastic properties of arm soft tissues on pressure transmission efficiency between the cuff and the brachial artery.In the third set，the effects of increased thickness of the subcutaneous fat layer on intra-arm pressure transmission were studied.The details of the three sets of computation conditions are summarized in Table 2.

3　Results

3.1Sensitivity of computed results to loading and contact conditions

Fig.4（Color online）Simulated pressure distributions in the upper arm under various loading and contact conditions a-c（corresponding to computation conditions of“Set 1”in Table 2）and the experimental data d（cuff bladder pressure is 150 mmHg，the unit of the labeled numbers is“mmHg”）［15］.a Uniform loading condition and bonded contactcondition.b Non-uniform loading condition and bonded contact condition.c Non-uniform loading condition and rough contact condition.Section“A-A”is the cross-section cutting through the upper arm beneath the center of the cuff

Figure 4 illustrates the pressure distributions in the center plane and a cross-section of the ideal arm model computed under different loading and contact conditions（for details of the applied loading and contact conditions，see“Set 1”in Table 2）.A cuff bladder pressure of 150 mmHg（1 mmHg= 133.3 Pa）was applied in all simulations.Note that to facilitate the comparison with experimental data，visualization of simulated results was restricted to the armtissuesbeneath the cuff.When a uniform cuff pressure distribution（see Fig.3a）and a bonded muscle-bone contact condition were applied，remarkable stress concentration was predicted in the near bone zone（Fig.4a），the degree of stress concentration was significantly reduced when a non-uniform cuff pressure distribution was applied instead of the uniform cuff pressure distribution（Fig.4b）.If the bonded muscle-bone contact condition was further replaced by a rough contact condition，stress concentration in the near-bone zone vanished（Fig.4c），and the simulated results agreed reasonably with the measured data（Fig.4d）in terms of both the pattern of pressuredistribution and the magnitude of pressure transmitted to the bone surface.

3.2The effects of cuff pressure on pressure transmission from the cuff to the brachial artery

Numerical experiments were performed on the anatomic modelto investigate the effects ofthe magnitude ofcuffpressure on the efficiency of pressure transmission from the cuff to the brachialartery.In these simulations，a non-uniformcuff pressure distribution and a rough muscle-bone contact condition were applied.Moreover，the length of the cuff was set to be 16 cm to represent a regular adult cuff used in noninvasive blood pressure measurement.Cuff bladder pressure was varied from 50 to 150 mmHg at an interval of 50 mmHg（see computation conditions“Set 2”in Table 2 for more details）. Panels a-c of Fig.5 illustrate the simulated pressure distributions in the arm tissues under different conditions.The simulated results for cuff bladder pressure of 150 mmHg（Panel c）were comparable to the experimental data（Panel d of Fig.4），although the width of cuff is different from that used in the experiment［15］.From Fig.5a-c，it is clear that the brachial artery experienced a varying external pressure along its axial direction，with the largest pressure appearing at the location just below the center of the cuff.The pressures imposed by cuffs of different bladder pressures on the brachialartery are furthercompared quantitatively in Fig.5d. Note that the plotted pressure values have been normalized by the corresponding cuff bladder pressures to facilitate the comparisons of pressure transmission efficiency from the cuff to the brachial artery.The magnitude of cuff bladder pressure was observed to slightly affect the proportion of cuff pressure transmitted to the brachial artery.

3.3The effects of the elastic properties of arm soft tissues on pressure transmission from the cuff to the brachial artery

The stiffness of the arm muscle was varied respectively by -10%and+10%relative to its baseline value to investigate its effects on intra-arm pressure transmission.In the simulations，cuffpressure was fixed at150 mmHg（see computation conditions“Set 2”in Table 2 for more details）.Obtained results showed that the variations in muscle elastic property induced little changes both in simulated pressure distributions in the arm tissues（Fig.6a-c）and in the efficiency of pressure transmission from the arm surface to the brachial artery（Fig.6d）.

3.4The effects of thickened subcutaneous fat layer on pressure transmission from the cuff to the brachial artery

In Fig.7，the intra-arm pressure distribution simulated for the regular arm model（panel a）is compared with those simulated for obese models（panels b and c）featured by the presence ofa thickened subcutaneous fatlayer（cuffpressure was fixed at 150 mmHg in all the simulations，see computation conditions“Set 3”in Table 2 for more details）.The subcutaneous fat layer significantly damped pressure transmission from the arm surface to the bone.For instance，adding a 2 cm subcutaneous fat layer to the regular arm model resulted in an over 15%（24 mmHg in absolute value）reduction in the maximum pressure detected at the bone.Accordingly，the external pressure experienced by the brachialartery was considerably attenuated as a consequence of the damping effects of the subcutaneous fat layer，with its maximum value decreasing from 127 mmHg（in the case of the regular model）to 104 mmHg（in the case of the obese modelwith a subcutaneous fatlayerof2 cm in thickness（see Fig.7d）.

4　Discussion

Bio-signals used to estimate blood pressures are generated through complex interactions among cuff，soft tissues，and hemodynamic variables in arteries.Theoretically，any changes in the interactions among these factors could affect the accuracy of blood pressure measurement.In the literature，attention has been paid primarily to hemodynamic factors or mechanical properties of brachial artery walls［11，12］.Although a few studies have addressed the interaction between cuff and soft tissues using FE models［13，14］，these studies were usually limited to simplified modeling of soft tissues，and，in particular，lacked a thorough validation of computed intra-tissue stresses against experimental data.Forexample，the numericalresults reported in Ref.［14］showed the presence of marked stress concentration in the near-bone region，which was inconsistent with the experimental data［15，16］.In the present study，we carried out a series of numerical experiments to uncover the factors that cause the discrepancies.Obtained results revealed that the application of a uniform cuff pressure distribution on arm surface in Ref.［14］was the major contributor to the simulated stress concentration phenomenon，with the bonded muscle-bone contact condition being the secondary contributor.When the loading and contact conditions adopted in Ref.［14］were replaced by a non-uniform cuff pressure distribution on the arm surface combined with a rough muscle-bone contact condition，stress concentration in the near-bone region vanished，and the simulated results showedreasonable agreements with the experimental data［15］.The non-uniform distribution of cuff pressure on the arm surface has been confirmed by previous experimental studies［15，16］.Mechanically，the non-uniform nature of cuff pressure distribution on the arm surface is a consequence of the deformation of arm tissues，which allows the generation of both axial and radial forces on the arm surface to balance the forces in the cuff bladder.The phenomenon is particularly pronounced atthe edges ofthe cuff，resulting in reduced normal components of force transmitted toward the bone.With regard to the contact condition between bone and muscle，since muscle and bone are anatomically connected via connective tissues rather than being fused together，imposing a bonded muscle-bone contact condition（which assumes a firm attachmentofthe muscle elements to the bone elements）in a model may be problematic.Our study did demonstrate that applying a rough instead of the bonded muscle-bone contact condition helped improve the comparisons between simulations and experiments.

Fig.5（Color online）Simulated pressure distributions in the upper arm under different loading conditions（conditions“Set 2”in Table 2）.a Cuff bladder pressure is 50 mmHg.b Cuff bladder pressure is 100 mmHg.c Cuff bladder pressure is 150 mmHg.d The effects of varying cuff bladder pressure on tissue pressure distribution along the outer wall of the brachial artery.Herein，the simulated tissue pressures have been normalized by the cuff bladder pressure to facilitate comparison.The maximum values of the normalized tissue pressures reflect the efficiency of pressure transmission from the cuff to the brachial artery

The elastic properties of arm soft tissues have been found to have little influence on intra-arm pressure transmission［13，14］，which was again confirmed by our numerical experiments（where the stiffness of arm muscle was varied by ±10%relative to the baseline value）（see Fig.6）.Our study furtherdemonstrated thatthe efficiency ofpressure transmission from the arm surface to the brachial artery is insensitive to the magnitude of cuff pressure as well（see Fig.5）. Although pressure transmission efficiency was observed to decrease when cuff pressure was elevated from 50 to 150 mmHg，the degree of decrease was fairly small.The finding impliesthatvariation in pressure transmission efficiency with cuff pressure may not be a key factor affecting the accuracy of noninvasive blood pressure measurement among subjects with different blood pressure conditions（e.g.，hypertensive subjects and normotensive subjects）.

Fig.6（Color online）Effects of varying the elastic properties of muscle on simulated pressure distribution along the outer wall of the brachial artery.a-c illustrate the simulated pressure distributions in the arm tissues under different conditions.a Baseline conditions.b Stiffness of arm muscle was reduced by 10%.c Stiffness of arm muscle was increased by 10%.d The normalized pressure distributions along the outer wall of the brachial artery.Herein，cuff bladder pressure was fixed at 150 mmHg in all the simulations，for more details of the computation conditions，see conditions“Set 2”in Table 2

For obese subjects，it has been found that there is a tendency to overestimate both systolic and diastolic pressures in noninvasive blood pressure measurement［10，17，29］.Our study demonstrated that the increased thickness of the subcutaneous fat layer in obese subjects remarkably damped the transmission of cuff pressure to the brachial artery.That is，given the same blood pressures in the brachial artery，to compress the brachial artery of an obese subject to the same degree as that of a normal subject，a higher cuff pressure is required in the obese subject，which would correspondingly result in overestimates of blood pressures if one employs the same criteria for determining blood pressures as in normal subjects.From the computed results for the obese arm with a subcutaneous fat layer of 20 mm in thickness，brachial pressures may be overestimated by over 23 mmHg if a regular cuff is used，which falls in the clinically determined range of pressure overestimate（2.4-30 mmHg）in obese patients［10，17］.However，it should be pointed out that the modeling of obesity is insufficient in the present study because，under in vivo conditions，obesity-associated changes in arm tissues are，featured mainly by，but not limited to thickening of the subcutaneous fat layer.Reconstructing arm models based on medical images taken from obese subjects would allow a more reasonable investigation of the problem.Despite the limitation，our numerical analysis for the first time revealed the biomechanical mechanisms behind the pressure overestimation phenomenon in the specific patient cohort.

In addition to the computation conditions discussed above（i.e.，loading，contact conditions，and mechanical properties of arm tissues），the anatomy of the arm represents another factor potentially affecting the picture of simulated pressure distribution in arm tissues.For instance，the intraarm pressure contours simulated for the anatomic model were asymmetric as opposed to the symmetric ones simulated for the ideal model.The pronounced pressure damping effectresulting from thickening ofthe subcutaneous fatlayer implies that the dimension and tissue component of the arm may considerably influence the transmission efficiency of pressure fromthe cuffto the brachialartery.Owing to the fact that the anatomical properties of arm vary from one individual to another，constructing a personalized arm model based on medical images would be necessary when the mechanical interaction between a cuff and the arm tissues of a specific individual is concerned.

Fig.7（Color online）Comparisons of simulated intra-arm pressure distributions a-c and pressures exerted on the brachial artery d between the regular and obese arm models（for detailed computation conditions，see conditions“Set 3”in Table 2）

There are several limitations associated with model setup and prescription of computation conditions.For example，we did not model the coupling of the arm and a real inflatable cuff，but instead accounted for the mechanical effects of cuff inflation by imposing a pressure load on the arm surface.Representing the inflation of an inflatable cuff using a three-dimensional FE model would be extremely complex because the governing equations of cuff mechanics（i.e.，the deformation of cuff bladder and outer walls）must be solved in combination with the aerodynamic equations that account for air compression in the cuff bladder［12，30］.In view of the fact that the distribution of cuff pressure load on the arm surface is derivable from previous experimental studies［15］，modeling a real cuff would not be expected to help us gain additionalinsights into the problems addressed in the present study.Anotherlimitation isthatwe setthe brachialartery wall to be free ofstressin the initialconditions.Underin vivo conditions，pulsatile blood pressures always exist in the brachial artery，which induce dynamic deformation of the artery and generate time-varying stresses in the artery wall.Since the present study focuses on investigating the transmission of pressure in arm tissues，neglecting the small deformation of brachialartery wallwould notsignificantly affectthe reliability ofournumericalanalysis.However，when the deformation behaviors of the brachial artery wall under an inflatable cuff are the major interest，intra-artery blood pressures should be taken into account.Moreover，the stress-strain relationships ofthe softtissueshave been derived fromstretch experiments rather than compression experiments.As a matter of fact，the mechanical properties of biomaterials may differ under stretch and compression conditions.From the simulated results，most principal strains in the under-cuff region were positive due to extrusion of materials to the ends of the arm segmentwhere a free stressboundary condition is prescribed. This implies that using the data obtained from stretch experiments to set material properties is reasonable for the present study.Nevertheless，it should be stressed that the ends of the modeled arm segment may not be completely stress free under in vivo conditions.To clarify the problem，extending the region ofarmmodeling（such as constructing a whole arm model）would be required.Finally，itis necessary to note that connective tissueslinking the muscle and bone have complex anatomical structures with nonlinear mechanical properties，to fully account for these features，a sophisticated anatomybased model rather than a simple contact model would be required.

5　Conclusions

FE models have been constructed to simulate stress distribution in arm tissues under an inflatable cuff.The numerical experiments demonstrated the necessity of applying proper loading and contact conditions to reproduce experimental observations.The magnitude of cuff pressure was found to have little influence on the efficiency ofpressure transmission in arm tissues，partly confirming the reliability of cuff-based noninvasive blood pressure measurement in both normotensive and hypertensive subjects.The finding that thickening of the subcutaneous fat layer in obese patients significantly damped the transmission ofcuffpressure in the arm tissues is of particular clinical relevance，which provides useful theoreticalevidence forexplaining the clinicalfindingsassociated with noninvasive blood pressure measurement in the specific patient cohort.The issue，however，remains to be addressedin a more sophisticated way，by，for example，constructing anatomically realistic obese arm models based on medical images.

Acknowledgments The project was supported in part by the National Natural Science Foundation of China（Grant 81370438）and the SJTU Medical-Engineering Cross-cutting Research Project（Grant YG2015MS53）.Zhipeng Deng was supported by the Hui-Chun Chin and Tsung-Dao Lee Chinese Undergraduate Research Program Endowment.

1.Franklin，S.S.，Khan，S.A.，Wong，N.D.:Is pulse pressure useful in predicting risk for coronary heart disease？The Framingham heart study.Circulation 100，354-360（1999）

2.Kannel，W.B.，Gordon，T.，Schwartz，M.J.:Systolic versus diastolic blood pressure and risk of coronary heart disease:the Framingham study.Am.J.Cardiol.27，335-346（1971）

3.Riva-Rocci，S.:Un sfigmomanometro nuovo.Gaz.Med.Torino. 47，981-996（1896）（in Italian）

4.Korotkoff，N.S.:K voprosu o metodoach eesldovania krovyanovo davlenia.Imperatoor.Vorenno.JzV.Med.Akad.11，365-367（1905）（in Russian）

5.Ohkubo，T.，Imai，Y.，Tsuji，I.，et al.:Home blood pressure measurement has a stronger predictive power for mortality than does screening blood pressure measurement:apopulationc-based observation in Ohasama，Japan.J.Hypertens.16，971-975（1998）

6.Agarwal，R.，Bills，J.E.，Hecht，T.J.W.，et al.:Role of home blood pressure monitoring in overcoming therapeutic inertia and improving hypertension control:a systematic review and meta-analysis. Hypertension 57，29-38（2011）

7.Cohn，J.N.:Blood pressure measurement in shock:mechanism of inaccuracy in auscultatory and palpatory methods.JAMA 199，972-976（1967）

8.Pickering，T.G.，Hall，J.E.，Appel，L.J.，etal.:Recommendationsfor blood pressure measurement in humans and experimental animals；part 1:blood pressure measurement in humans:a statement for professionals from the Subcommittee of Professional and Public Education of the American Heart Association Council on High Blood Pressure Research.Hypertension 45，142-161（2005）

9.Sebo，P.，Pechère-Bertschi，A.，Herrmann，F.R.，et al.:Blood pressure measurements are unreliable to diagnose hypertension in primary care.J.Hypertens.32，509-517（2014）

10.Halm，M.A.:Arm circumference，shape，and length:how interplaying variables affect blood pressure measurement in obese persons. Am.J.Crit.Care 23，166-170（2014）

11.Liang，F.Y.，Liu，H.，Takagi，S.:The effects of brachial arterial stiffening on the accuracy of oscillometric blood pressure measurement:A computational model study.J.Biomech.Sci.Eng.7，15-30（2012）

12.Ursino，M.，Cristalli，C.:A mathematical study of some biomechanical factors affecting the oscillometric blood pressure measurement.IEEE Trans.Biomed.Eng.43，761-778（1996）

13.Cristalli，C.，Ursino，M.:Influence of arm soft tissue on noninvasive blood pressure measurements:an experimental and mathematical study.Measurement 14，229-240（1995）

14.Lan，H.，Al-Jumaily，A.M.，Lowe，A.，etal.:Effectoftissue mechanical properties on cuff-based blood pressure measurements.Med. Eng.Phys.33，1287-1292（2011）

15.Hargens，A.R.，McClure，A.G.，Skyhar，M.J.，etal.:Localcompression patterns beneath pneumatic tourniquets applied to arms and thighs of human cadavera.J.Orthop.Res.5，247-252（1987）

16.Crenshaw，A.G.，Hargens，A.R.，Gershuni，D.H.，etal.:Wide tourniquetcuffs more effective atlowerinflation pressures.Acta.Orthop. 59，447-451（1988）

17.Palatini，P.，Parati，G.:Blood pressure measurement in very obese patients:a challenging problem.J.Hypertens.29，425-429（2011）

18.Ogden，R.W.:Non-Linear Elastic Deformations.Courier Corporation.Dover Publications，New York（1997）

19.Holzapfel，G.A.:Nonlinear Solid Mechanics:A Continuum Approach for Engineering.Wiley，Chichester（2000）

20.Dubuis，L.，Avril，S.，Debayle，J.，etal.:Identification ofthematerial parameters of soft tissues in the compressed leg.Comput.Method. Biomech.15，3-11（2012）

21.Tang，C.Y.，Zhang，G.，Tsui，C.P.:A 3d skeletal muscle model coupled with active contraction of muscle fibres and hyperelastic behaviour.J.Biomech.42，865-872（2009）

22.Ansari，M.，Lee，S.K.，Cho，C.D.:Hyperelastic muscle simulation. Key Eng.Mater.345，1241-1244（2007）

23.Masson，I.，Boutouyrie，P.，Laurent，S.，et al.:Characterization of arterialwall mechanical behavior and stresses from human clinical data.J.Biomech.41，2618-2627（2008）

24.Calvo，B.，Ramírez，A.，Alonso，A.，et al.:Passive nonlinear elastic behaviour of skeletal muscle:experimental results and model formulation.J.Biomech.43，318-325（2010）

25.Hwang，W.，Carvalho，J.C.，Tarlovsky，I.，et al.:Passive mechanics of canine internal abdominal muscles.J.Appl.Physiol.98，1829-1835（2005）

26.Azar，F.S.，Metaxas，D.N.，Schnall，M.D.:Methods for modeling and predicting mechanical deformations of the breast under external perturbations.Med.Image.Anal.6，1-27（2002）

27.Martin，R.B.，Burr，D.B.，Sharkey，N.A.:Skeletal Tissue Mechanics.Springer，New York（1998）

28.Bronner，F.，Farach-Carson，M.C.，Mikos，A.G.:Engineering of Functional Skeletal Tissues.Springer，New York（2007）

29.Pierin，A.M.，Alavarce，D.C.，Gusmao，J.L.，et al.:Blood pressure measurementin obesepatients:comparison between upperarmand forearm measurements.Blood Press.Monit.9，101-105（2004）

30.Liang，F.Y.，Takagi，S.，Himeno，R.，et al.:A computational model of the cardiovascular system coupled with an upper-arm oscillometric cuff and its application to studying the suprasystolic cuff oscillation wave，concerning its value in assessing arterialstiffness. Comput.Methods Biomech.Biomed.Eng.16，141-157（2013）

4 September 2015/Revised:5 May 2016/Accepted:9 May 2016/Published online:22 July 2016

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics，Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016